Analysis of Partial Volume Effects on Accurate Measurement of the Hippocampus Volume

Maryam Hajiesmaeili, Jamshid Dehmeshki, and Tim Ellis

Analysis of Partial Volume Effects on Accurate Measurement of the Hippocampus Volume

Maryam Hajiesmaeili, Jamshid Dehmeshki, and Tim Ellis

—Hippocampal volume loss is an important biomarker in distinguishing subjects with Alzheimer’s disease (AD) and its measurement in magnetic resonance images (MRI) is influenced by partial volume effects (PVE). This paper describes a post-processing approach to quantify PVE for correction of the hippocampal volume by using a spatial fuzzyC-means (SFCM) method. The algorithm is evaluated on a dataset of 20 T1-weighted MRI scans sampled at two different resolutions. The corrected volumes for left and right hippocampus (HC) which are 23% and 18% for the low resolution and 6% and 5% for the high resolution datasets, respectively are lower than hippocampal volume results from manual segmentation. Results show the importance of applying this technique in AD detection with low resolution datasets.

Index Terms—Hippocampus, magnetic resonance images, partial volume effects, spatial fuzzyC-means.

1. Introduction

Accurate quantification of structures in medical imageries can provide essential details for diagnosis, treatment planning, and follow-up comparisons. Increasingly, image analysis needs to generate reliable quantitative information to support clinical decisions and feature analysis is an important step, enabling robust extraction of structures of interest. Reconstruction of 3-dimansion (3D) brain scans allows volumetric quantification of anatomical structures such as the hippocampus. The magnetic resonance imaging (MRI) intensity at each voxel is summed over the corresponding anatomical volume, as determined by the (finite) spatial resolution of the imaging scanner. However, at the boundary more than one tissue type is presented in each voxel (i.e. it is a mixed voxel), and signals from different tissue types contribute to the partial volume effect (PVE), where an unknown proportion of the voxel can be associated with the tissue of interest. This paper proposes a method for estimating PVE in order to generate more accurate measurements of the hippocampal volumes.

The progression of Alzheimer’s disease (AD) is detectable as subtle changes of the hippocampal volumes, but the detection requires accurate and robust image segmentation. In a previous paper[1], we have proposed a level set approach, but because of multiple imaging artifacts, such as intensity in homogeneities and PVE, the resulting volumetric measurements are not sufficiently accurate to reliably detect these changes.

In this paper, we present a pre-segmentation step to provide for bias correction of nonuniform image intensity’s using a fuzzy C-means method (BCFCM) and a post-segmentation step to account for the PVE on hippocampal volume quantification. The PVE correction uses a spatial fuzzy C-means (SFCM) algorithm to estimate the proportion of a bounding surface voxel corresponding to HC (internal) or other tissue external to the bounding surface. Section 2 provides a review of the literature related to PVE estimation. Section 3 presents a description of the proposed method by introducing bias corrected fuzzy C-means and spatial fuzzy C-means as post-processing. Section 4 evaluates the performance of the PVE correction algorithm on 20 MRI patient datasets acquired at two different spatial resolutions and describes the experimental results. Finally, Section 5 provides conclusions.

2. Literature Review

In the last two decades, increasing attention has been paid to minimizing the effect of partial volumes in order to improve the accuracy of quantitative measurements. The PVE is an important image-related factor to be estimated in order to obtain subvoxel accuracy. Choi et al.[2]derived an algorithm based on a Markov random field (MRF) model that is made less sensitive to noise by smoothing the result, whilst Mazinani[3]applied a hybrid Markovian fuzzy C-means approach by considering spatial information for segmentation of the blood vessel. However, both methods, which are based on MRF, suffer from a high computation cost in determining the correct parameters and theweighting between the prior and the data. Zadeh et al.[4]developed a method that depends on registered image sequences to create images with intensities proportional to the quantity of a certain tissue in each voxel. Roll et al.[5]assigned a tissue type tag to each voxel by applying an intensity thresholding segmentation approach and correction of PVE depending on all voxels in an image, not just the PVE voxels.

Using a statistical approach, [6] and [7] described the behavior of the proportion of each tissue in mixed voxels by using a Gaussian model with a uniform distribution for the tissue classes based on the tissue mean intensity and variance. Alternatively, [8] and [9] employed the same tissue model with the same variance for all tissues and presented an algorithm for mean estimation to fit the distribution to the histogram of the whole image. However, the results without any quantitative comparison with other methods do not give a reliable method for a small structure such as the hippocampus. Reference [10] presented a regression algorithm that corrected for PVE in arterial spin labeling (ASL) where the voxel intensities were computed as a weighted sum of the pure tissue contribution and the weighting coefficients were the tissue’s fractional volumes in the voxel. However, this approach is not applicable for a T1-weighted dataset. Reference [11] presented a method with the same drawback as [6], but the tissue distributions were not limited to Gaussian’s with a common variance. In [12], an expectation-maximization (EM) approach was used to simultaneously estimate the parameters of the resulting model and perform a papillomavirus (PV) classification in brain MR images. However, it is difficult to estimate the EM parameters for a small structure like the HC because EM (as the maximum likelihood model) does not consider the spatial information. Estimation of PVE is required to separate HC tissue from the other tissues while considering uncertainties in the boundary of regions. In particular, the fuzzy C-means algorithm has been used for quantifying PVE[13],[14]. In this method, an objective function for partitioning voxels into different clusters is achieved without consideration of the effect of neighboring voxels. In [15], Dehmeshki proposed a modified expectation-maximization (MEM) that is less sensitive to noise and PVE to determine the volume of calcium in the calcified region of the coronary vessel wall, for computed tomography (CT) images which is superior to the voxel-based (130) HU thresholding method but is not appropriate for the volumetric quantification of the HC in a MRI brain scan.

3. Methods

Fig. 1 illustrates the program flow of our algorithm. In MR images, homogeneities in the magnetic field caused by nonuniform tissue intensities are typically characterized by a slowly varying gain field called the bias field. Bias correction based on a fuzzy C-means method (BCFCM)[16]can be used in a pre-processing step prior to level set segmentation. The hippocampal volumes obtained from the level set segmentation results are unreliable because of PVE. Hence, we need to account for this effect with a volume correction. Using manually annotated ground truth images, it is possible to evaluate the quality of our level set segmentation compared with the ‘true’ hippocampal volumes using the Dice metric. The Dice metric takes values from zero to one, where higher values indicate better agreement. Hence, for the threshold of the proposed method is 85%, sets on segmentation alleviate the effect of poor results (over-segmentation or under-segmentation) and encourage the algorithm to employ reliable results for PVE correction. For PVE estimation, spatial fuzzy C-means (SFCM) is presented to find the membership degree for each tissue contributes to determine voxel intensity. To measure the corrected volumes of HC, the nontissue border volumes with respect to achieved membership degree will be deducted from the segmentation result volumes.

3.1 Bias Correction

The application of a logarithmic transformation to the intensities allows the artifact to be modelled as an additive bias field:

where xland ylare the true and observed log-transformed intensities at the lth voxel and βlis the bias field at the lth voxel.

We use an iterative algorithm based on fuzzy logic to estimate the unknown gain field. The standard FCM objective function for partitioninginto c clusters is

Fig. 1. Algorithm for implementing proposed approach.

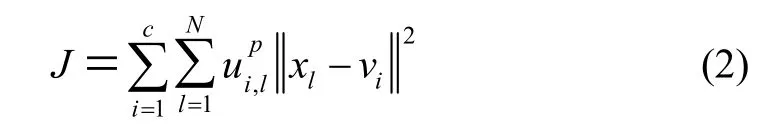
By considering (2) and adding a regularizer term, the modified objective function is given by

The parameter p determines the amount of fuzziness of the resulting classification, Nlis the set of neighbours around xland the cardinality of Nlis NR. The parameter αcontrols the effect of the neighbor term. Taking the first derivative of Jmwith respect to βland setting it to zero, the bias field estimator is expressed as

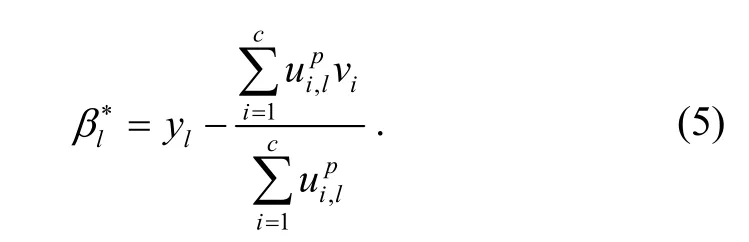
3.2 Partial Volume Correction by Spatial FuzzyC-Means (SFCM)

A region-based level set formulation is applied to the bias corrected image for HC segmentation, for which the curve evolution equation is derived for energy minimization[1]as follows:

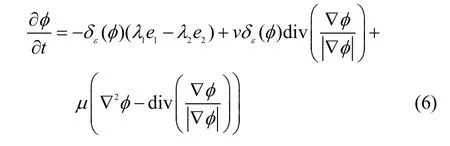
The stopping condition for the level set algorithm compares the evolving boundary with the manually annotated ground truth using the Dice metric to determine the degree of overlap. An empirical threshold of 85% is used to terminate the curve evolution.

A. Spatial Fuzzy C-Mean

The spatial relationship of pixels is an important element that is lacking in a conventional fuzzy C-means approach. SFCM uses pixel intensities, the location, and the correlation between neighboring pixels in order to address this deficiency, as defined in:

where p and q are parameters to control the relative importance of both functions. Hence, the average degree of membership over all the voxels in boundary estimates the partial contribution of each tissue to the voxel intensity.

B. Volume Correction

The HC volumes measurement resulting from level set segmentation Vsis corrected by subtracting each the volume of border voxels Vbweighted by the average membership degree of non-tissue (AMDN):

4. Experimental Results

Experimental results are evaluated on 20 T1-weighted MRI head scans acquired using two different spatial resolutions. Ten scans were acquired with a General Electric 1.5T (GE Medical Systems, Milwaukee WI) with a pixel size of 0.78 mm×0.78 mm and a slice thickness of 2.00 mm. A further ten scans were acquired with a General Electric 3.0 T system with a pixel size of 0.39 mm×0.39 mm and slice thickness of 2.00 mm. The dataset including manual annotation of the left and right HC was generated by the Department of Diagnostic Radiology at the Henry Ford Hospital (HFH)[17]. The annotations were used as comparative segmentation ground-truth. Fig. 2 shows the result of bias correction for a sagittal slice of one of the MRI scans. Fig. 3 shows the result of the level set segmentation of the bias corrected slice shown in Fig. 2 and its correspondent binary result.

Fig. 2. Bias field correction: (a) original image, (b) estimated bias image, and (c) bias corrected image.

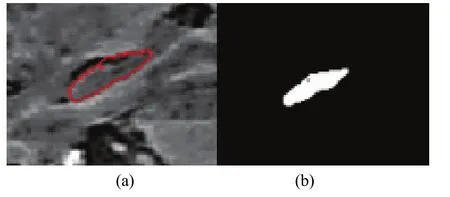
Fig. 3. Segmentation result: (a) HC boundary detected by level set segmentation and (b) resulting binary image.

Refinement of the segmentation results are vital to access high accuracy results and avoid propagating segmentation errors to the PVE correction step. Hence the Dice value is used for making decision to return poor results for resegmentation or to shift for PVE correction. In the proposed algorithm, any result with the Dice value 0.85 or higher is adequate for PVE step. For instance, the Dice value for the left HC of dataset HFH_001 is 0.86 which is acceptable for applying post-processing technique while the same value for dataset HFH_008 is 0.79 and then resegmentation is required.

Each acceptable result should be classified into two clusters using SFCM: the HC as a tissue and the rest as nontissue. This technique applied to 20 datasets and the average of membership degree for HC and nontissue are obtained 0.11 and 0.89, respectively. Table 1 and Table 2 show the corrected volume estimates for the left and right HC of 10 low resolution and 10 high resolution MRI scans.

Multiplication of the percentage of volumes by segmentation volumes gives PVE volume correction and the comparisons of these results in Table 1 indicates lower amount for percentages of volumes in low resolution datasets, which are 72% for left and 74% for right HC and then more reduction for segmentation volume results more PVE. On the other hand, Table 2 for high resolution datasets shows greater volumes percentages in high resolution datasets, which are 86% for left and 88% for right HC, so it will obtain less reduction in segmentation volumes and also less PVE. Consequently, the corrected volumes of left and right HC for Table 1 are 23% and 18% less than ground truth volumes of HC but the same amount for high resolution datasets in Table 2 are 6% and 5% less than ground truth volumes.

In addition, to detect Alzheimer’s disease, HC volumes for low resolution datasets which are more significant, is compared with the HC volumes in [18], which can be used as criteria (CR) to distinguish patient ones.

Table 1: Original and corrected volumes (mm3) for left and right HC for 10 low resolution MRI scans

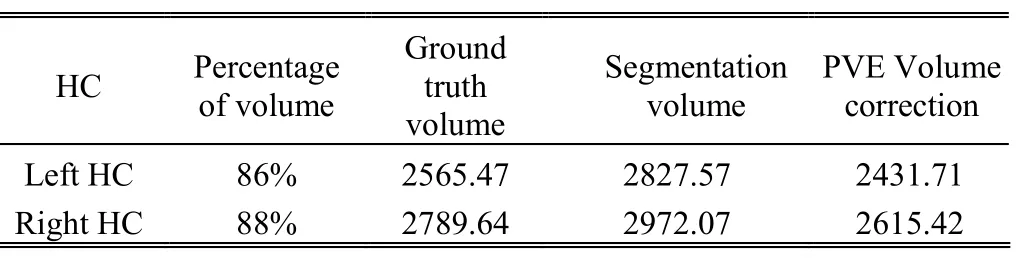
Table 2: Original and corrected volumes (mm3) for 10 high resolution MRI scans

Table 3: Average volume for 10 patient MRI datasets with low resolution and the comparison with results in [18] (mm3) for CR

Table 3 shows the average range of HC volumes for subjects with AD and the results for HC volumes for the proposed method before correction and after considering PVE. Segmentation volumes for the left and right HC in the first column compare with the CR volumes in the third column then it will be considered as the normal subject because they are not in the CR interval while the comparison between PVE volumes in the second column and CR volumes recognizes this scan as the patient subject.

5. Conclusions

In this paper, we proposed a technique for correction of PVE to obtain accurate measurement of left and right HC volumes to track subtle changes in volumes as a main biomarker for the detection of Alzheimer’s disease. Bias corrected fuzzy C-means was applied for bias estimation as preprocessing and spatial fuzzy C-means as post-processing to find membership degree for nontissue cluster to measure PVE for each voxel. This technique was tested on MRI images and evaluated by HC ground truth volumes for two different resolution datasets and the experimental results show the importance of applying the proposed method for low resolution datasets.

[1] M. Hajiesmaeili, B. Bagheri, J. Dehmeshki, and T. Ellis,“Segmentation of the Hippocampus for detection of Alzheimer’s disease,” in Advances in Visual Computing, Rethymnon: Springer, 2012, pp. 42-50.

[2] H. S. Choi, D. R. Haynor, and Y. Kim, “Partial volume tissue classification of multichannel magnetic resonance images-a mixel model,” IEEE Trans. on Medical Imaging, vol. 10, no. 3, pp. 395-407, 1991.

[3] M. Mazinani, “Computer aided detection and measurement of coronary artery disease from computed tomography angiography images,” Ph.D. dissertation, Faculty of Science, Engineering and Computing, School of Computing and Information Systems, Kingston University London, 2012.

[4] H. Soltanian-Zadeh, J. P. Windham, and A. E. Yagle,“Optimal transformation for correcting partial volume averaging effects in magnetic resonance imaging,” in Proc. of Nuclear Science Symposium and Medical Imaging Conf., Orlando, 1992, 1289-1291.

[5] S. A. Röll, A. C. F. Colchester, P. E. Summers, and L. D. Griffin, “Intensity-based object extraction from 3D medical images including a correction of partial volume errors,” in Proc. of British Machine Vision Conf.,Edinburgh, 1994, pp. 205-214

[6] P. Santago and H. D. Gage, “Quantification of MR brain images by mixture density and partial volume modeling,”IEEE Trans. on Medical Imaging, vol. 12, no. 3, pp. 566-574, 1993.

[7] P. Santago and H. D. Gage, “Statistical models of partial volume effect,” IEEE Trans. on Image Processing, vol. 4, no. 11, pp. 1531-1540, 1995.

[8] D. H. Laidlaw, K. W. Fleischer, and A. H. Barr,“Partial-volume Bayesian classification of material mixtures in MR volume data using voxel histograms,” IEEE Trans. on Medical Imaging, vol. 17, no. 1, pp. 74-86, 1998.

[9] C. Jaggi, S. Ruan, and D. Bloyet, “Mixture modeling applied to the partial volume effect in MRI data,” in Proc. of the 20th Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society, Berlin, 1998, pp. 693-695

[10] I. Asllani, A. Borogovac, and T. R. Brown, “Regression algorithm correcting for partial volume effects in arterial spin labeling MRI,” Magnetic Resonance in Medicine, vol. 60, no. 6, pp. 1362-1371, 2008.

[11] M. Á. G. Ballester, A. P. Zisserman, and M. Brady,“Estimation of the partial volume effect in MRI,” Medical Image Analysis, vol. 6, no. 4, pp. 389-405, 2002.

[12] K. Van Leemput, F. Maes, D. Vandermeulen, and P. Suetens,“A unifying framework for partial volume segmentation of brain MR images,” IEEE Trans. on Medical Imaging, vol. 22 no. 1, pp. 105-119, 2003.

[13] M. E. Brandt, T. P. Bohant, L. A. Kramer, and J. M. Fletcher,“Estimation of CSF, white and gray matter volumes in hydrocephalic children using fuzzy clustering of MR images,” Computerized Medical Imaging and Graphics, vol. 18, no. 1, pp. 25-34, 1994.

[14] D. L. Pham and J. I. Prince, “Partial volume estimation and the fuzzy C-means algorithm [brain MRI application],” in Proc. of Int. Conf. on Image Processing, Chicago, 1998, pp. 819-822.

[15] J. Dehmeshki, X. Ye, H. Amin, M. Abaei, X. Lin, and S. D. Qanadli, “Volumetric quantification of atherosclerotic plaque in CT considering partial volume effect,” IEEE Trans. on Medical Imaging, vol. 26, no. 3, pp. 273-282, 2007.

[16] M. N. Ahmed, S. M. Yamany, N. Mohamed, A. A. Farag, and T. Moriarty, “A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data,” IEEE Trans. on Medical Imaging, vol. 21, no. 3, pp. 193-199, 2002.

[17] K. Jafari-Khouzani, K. Elisevich, S. Patel, and H. Soltanian-Zadeh, “Dataset of magnetic resonance images of nonepileptic subjects and temporal lobe epilepsy patients for validation of hippocampal segmentation techniques,”Neuroinformatics, vol. 9, no. 4, pp. 335-346, 2011.

[18] L. Wang, J. S. Swank, I. E. Glick, M. H. Gado, M. I. Miller, J. C. Morris, and J. G. Csernansky, “Changes in hippocampal volume and shape across time distinguish dementia of the Alzheimer type from healthy aging,” NeuroImage, vol. 20, no. 2, pp. 667-682, 2003.

Maryam Hajiesmaeiliwas born in Tehran, Iranian in 1980. She received B.S. and M.S. degrees in applied mathematics from Azad University, Karaj, Iran in 2002 and 2004, respectively. Since 2011, she has studied for her Ph.D. degree in medical image processing with Kinston University,London,United Kingdom (U.K.). She is currently doing her research as part of the Ph.D. in accurate segmentation of the hippocampus. She is a member of Medical Imaging International Institute (QMI3) and Digital Imaging Research Centre (DIRC), Faculty of Science, Engineering and Computing, Kingston University London, U.K.

Jamshid Dehmeshkireceived the Ph.D. degree in image processing from the University of Nottingham, Nottingham, U.K. in 1997. He joined Kingston University, London, U.K., and leads the QMI3. He joined the Nuclear Magnetic Resonance (NMR) Research Unit, Institute of Neurology,University College London, as a senior research fellow and lecturer in 1999. From 2001 to 2006, as a Chief Technology Off i cer of the company Medicsight, he established and led research and development on image processing, scientif i c research, software development, and testing. His main research interests include developing computer-aided detection/diagnostic and measurement algorithms for quantitative analysis of medical images. He is also a member of DIRC, Faculty of Science, Engineering and Computing, Kingston University London, U.K.

Tim Ellisreceived the fi rst degree in physics from the University of Kent, Canterbury, Kent, U.K. in 1974 and the Ph.D. degree in biophysics from London University, London, U.K. in 1981. He joined City University in 1979. In 2003, he moved to Kingston University, London, where he was, until recently, the Dean of the Faculty of Computing, Information Systems and Mathematics. His research interests include visual surveillance, industrial inspection, colour image analysis, and vision systems hardware. Professor Ellis cochaired the 2004 British Machine Vision Conference. He is a member of the Institution of Engineering and Technology and was the exchair of the British Machine Vision Association and he is also a member of QMI3 and, Faculty of Science, Engineering and Computing, Kingston University London, United Kingdom.

Manuscript received March 19, 2013; revised June 16, 2013.

M. Hajiesmaeili is with Quantitative Medical Imaging International Institute and Digital Imaging Research Centre, Faculty of Science, Engineering and Computing, Kingston University London, Kingston upon Thames, KT1 2EE, United Kingdom (Corresponding author e-mail: m.hajiesmaeili@kingston.ac.uk).

J. Dehmeshki and T. Ellis are with Quantitative Medical Imaging International Institute and Digital Imaging Research Centre, Faculty of Science, Engineering and Computing, Kingston University London, Kingston upon Thames, KT1 2EE, United Kingdom (e-mail: J.Dehmeshki@kingston.ac.uk; T.Ellis@kingston.ac.uk).

Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.02.008