Review on Applications of 3D Inverse Design Method for Pump
YIN Junlian and WANG Dezhong
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
1 Introduction
For the hydro dynamic design of turbomachinery it is often desirable to solve the inverse problem, especially for designs without any reference. Using an inverse-design method, the performance characteristics are prescribed by the blade loading distribution, and the corresponding geometry is obtained simultaneously as a result of an inverse analysis. Both the flow field and the geometry are obtained from this procedure. The inverse design method was first outlined by HAWTHORNE, et al[1]and TAN, et al[2], then developed by BORGES[3], ZANGENEH, et al[4–5].There are several key features of the 3D inverse design methodology. (1) Compared to the traditional design methods based on geometry parameters[6–7], the design is controlled by hydrodynamic parameters, i.e., the blade loading distributions or pressure distribution[8]. (2) This method can deal with the 3D flow effects so easily that designers can obtain a good understanding of the formation of secondary flows and from this know how to eliminate undesirable flows, such as blade-to-blade flow and hub-to-shroud flow. The costs associated with optimization processes can be significantly reduced with this knowledge.(3) It is universal for all types of designs for turbo machines such as pumps, turbines, pump turbines,compressors and fans. Regarding the shape of the blade,large differences, as shown Fig. 1, can be distinguished from the 3D inverse design and conventional design. The blade angle distribution of a conventionally designed impeller is usually very uniform because the 3D geometry is modelled by the conformal mapping method; while, by the 3D inverse method, the blade angle is directly computed by the given hydrodynamic parameters. However,the widespread adoption of such an approach by designers is inhibited by the difficulty of them being able to obtain the suitable blade loading distribution and stacking conditions.

Fig. 1. Comparison of blade angle distribution between conventional design and 3D inverse design
With the aim of identifying some rules, from successful design cases reported in the literature, the theory and applications of the 3D inverse design method are reviewed.The structure of this paper is arranged as follows: first, the fundamental inverse design theory and how the blade loading is related to the 3D flow effect is summarized in section 1 and section 2. Subsequently, referring to the previous works and authors’ experiences in engineering design, different modes of blade loading distribution given in several types of pumps with different specific speeds are discussed in section 3. In section 4, the principle and application of the stacking condition is summarized from several design cases. The coupling of the 3D inverse design method with modern optimization techniques is reviewed in section 5. Finally, the conclusions are drawed in section 6.
2 Basic Theory of Inverse Design Method
Given the flow rate Q and the head H, the task for hydraulic design is to construct an optimal geometrical boundary. To begin with, the input conditions for 3D inverse design are listed in Table 1. How can a perfect impeller or vane be obtained using the listed parameters and the 3D inverse design method?

Table 1. Input parameters for the 3D inverse design approach
In the 3D inverse design method, the blades are represented by sheets of vorticity whose strength is directly related to the specified bound circulation orAlso,from the angular momentum conservation law, the head can be expressed as
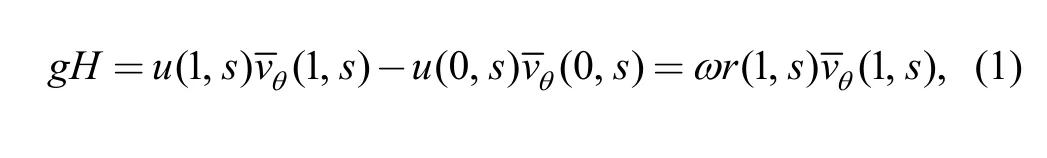
where g denotes the acceleration due to gravity, u is rotational velocity,is the pitch-averaged component of absolute velocity, ω is the angular velocity of rotation, r is the radial coordinate and s is the spanwise non-dimensional coordinate. And


where N denotes the blade number.
In this method, the variableis the known input parameter. The next step is to pose an algorithm to compute the 3D blade shape. Conventionally, with some other initial conditions (i.e., the stacking conditions), using the impenetrability condition (Eq. (4)) and an Euler solver based on a numerical method, such as the finite difference method or finite element method, a final blade shape satisfying the impenetrability condition and given blade loading distribution is simultaneously obtained. For details,readers can refer to the work by ZANGENEH, et al[5]or WESTRA[9].

The well-posed theory and advanced numerical methods have already been integrated into the commercial software Turbodesign by ZANGENEH[10]and GOTO, et al[11].
3 Theory of Suppression of Secondary Flow
As mentioned earlier, it is easy to understand and control the 3D flow effect with the 3D inverse design method. This means that determining the method to relate the 3D flow effect to the design parameters is the main question. For this purpose, it is useful to consider the following simple kinetic equation derived by ZANGENEH,et al[12]for incompressible flow:

where Ω represents vorticity anddenotes the streamwise component of absolute vorticity. The streamwise component of vorticity and secondary flows are generated where there is a component of acceleration(streamline curvature or Coriolis) in the direction of the absolute vorticity. According to the momentum equation for inviscid flow (Eq. (6)), the secondary flow can be ascribed to the pressure gradient.

where p denotes pressure and the pressure difference between the pressure side and the suction side can be derived according to the Bernoulli equation in the rotating frame. Assuming the blade thickness is zero, i.e., ups= uss,the pressure difference can be written as


where m denotes the coordinates of the meridional direction.
The integration is performed along a circular arc(d c = rd) and the blades are assumed to be of an infinitesimally small thickness, i.e., considering the following transformation relationship

where β is the angle between the circumferential direction and the direction l, which is tangent to the blade surface.Substitution of Eq. (8) and Eq. (9) into Eq. (7) gives:

Based on Eq. (10), the secondary flow is related to the pressure differencep , which in turn depends on the. Hence, the suppression of secondary flow can be controlled by the gradient of. The next question is how to obtain a suitable gradient ofdistribution,which will be discussed in the following section.
4 Blade Loading Distribution
For the blade loading distribution, the first values to be set should be those at the leading and trailing edges.According to the Kutta condition, the pressures at the pressure and the suction sides are equal. Following Eq. (10),the blade loadings at the leading edge and trailing edge are expressed as:

However, as pointed out by JIANG, et al[13], due to the difference between the ideal inviscid flow and the real viscid flow, the Kutta condition does not have to be satisfied. For convenience and generality in code programming, the Kutta condition is always adopted.
As mentioned earlier, the 3D effect is very obvious in the flow regime in turbomachinery, which can be identified by the secondary flow from the hub to the shroud, which, as an example, is shown in Fig. 2 from WATANABE, et al[14]and ZANGENEH, et al[5]. Due to this undesirable flow located in the impeller, the efficiency and stability of the whole pump will be reduced.

Fig. 2. Velocity vectors on the suction surface of a mixed flow pump[5] and a radial turbine[14]
According to Eq. (6), the secondary flow is induced by the pressure difference between the hub and the shroud. To suppress its occurrence, the blade loadings at the hub and shroud should be different and coupled with each other. To obtain an insight into how to set the blade loading distribution in the streamwise direction and spanwise direction, several typical and successful designs including centrifugal pump, mixed flow pump and axial flow pump are summarized, which are arranged by the specific speed nsdefined with the parameters under the best efficiency point (BEP):

where Q —Volumetric flow rate (m3/s),
H —Head (m),
n —Rotational speed (r/min).
Fig. 3 shows the meridional passage and the corresponding blade loading distribution in a centrifugal pump (Q=0.027 m3/s, H=55 m, n=2900 r/min, ns=86,case 1) and Fig. 4 shows this information (Q=0.241 m3/s,H=40 m, n=1000 r/min, ns=114, case 2) for a pump turbine. The blade loading distribution at the mid-span streamline is interpolated from those at the hub and shroud linearly. These two cases were designed by the authors and the blade loading is described. In addition there are three more cases, including a mixed flow pump (Q=0.054 m3/s,H=8.77 m, n=800 r/min, ns=133.5, case 3) by ZANGENEH[4]shown in Fig. 5, a Francis turbine runner(ns=200, case 4) shown in Fig. 6 by DANESHKAH, et al[16]and an axial flow pump (ns=474.5, case 5) shown in Fig. 7 by BONAIUTI, et al[17], also summarized.

Fig. 3. Schematic map of meridional passage and the applied blade loading distribution in a centrifugal pump (ns=86)

Fig. 4. Schematic map of meridional passage and the applied blade loading distribution in a pump turbine (ns=114)

Fig. 5. Meridional shape and blade loading distribution for a centrifugal flow pump (ns=152) from Ref. [4]

Fig. 6. Meridional shape and blade loading distribution for a Francis turbine runner (ns=200) from Ref. [16]

Fig. 7. Meridional shape and blade loading distribution in an axial flow pump designed by BONAIUTI, et al[17] (ns=474.5)
For designers, it may be desirable to get a quantitative guideline to set the blade loading distributions.Nevertheless, it is difficult due to the design limitations,such as transported fluid properties, cavitation requirement and manufacture, et al. Moreover, one meridional passage can be used in pump designs with different specific speeds.Though such factors as mentioned above exist, some qualitative guidelines can be identified from the listed design cases. First, from the authors’ experience, the mid-loaded distribution type adopted in case 1 and case 2 can also be adjusted to suppress the secondary flow. Also,as outlined by ZANGENEH from case 3 and case 4, a combination of fore-loaded hub and aft-loaded shroud is favorable with regards to the centrifugal pump and mixed flow pump. Thus, the key point for suppressing secondary flow does not depend on the type of distribution but on the ratio of blade loading distribution of the hub to the shroud,which is also validated by the case of the Francis runner(case 4), in which the mid-loaded hub and fore-loaded shroud is applied. Thus, the first guideline for centrifugal or mixed pumps and turbines is that the ratio of blade loading on the hub to that on the shroud should be more than the unit in the fore part of the blade. Whereas, in the aft part,the ratio should be decreased to satisfy the same wrap angle for both the hub and the shroud.
The principle for the choice of blade loading distribution is discussed in detail by ZANGENEH, et al[4–5]. Recalling Fig. 2, the secondary flow is always flowing from the hub to the shroud, which implies that a relative pressure difference exists. According to Eq. (10), to approach an equivalent state, the blade loading on the low pressure side(shroud) needs to be strengthened. Also from Eq. (5), the sources responsible for secondary flow are the curvature of the meridional shape and the Coriolis force. To distinguish different sources in different parts of an impeller, three parts (inducer, axial-radial and radial) were identified by ZANGENEH, et al[4]. They concluded that in the axial-radial part the meridional curvature can induce secondary flows from the hub to shroud and blade-to-blade secondary flow can be ascribed to the tangential component of the Coriolis, which is also true for the radial part. Here,the forces due to meridional curvature are surface-type and differ from design to design, while the Coriolis force is a body force, which exists in all fluid domains intrinsically.Considering the meiridional shapes, it is clear that the curvature of a shroud is larger than that of a hub, which causes a larger hydraulic loss and then a reduction in the meridional velocity. According to Eq. (10), the blade loading distribution on the shroud should be set to be larger than that on the hub. Therefore, the side with the larger curvature should be given the larger blade loading value,this is the second guideline related to the blade loading.
To validate this, Fig. 7 shows how the blade loading is distributed in an axial flow pump, from BONAIUTI, et al[17]. It can be seen that, compared with cases of centrifugal and mixed flow pumps, the blade loading on the hub is larger than that on the shroud. This is also the case in the inverse designed pump diffuser (case 6) from GOTO, et al[18]. Fig. 8 shows the meridional shape and the blade loading adopted for suppressing the secondary flow. The reason for this choice of the blade loading distribution can also be explained by the meiridional curvature. Especially in case 6, without the existence of the Coriolis effect, the curvature of the hub is larger so that a relative larger blade loading is applied on the hub.

Fig. 8. Blade loading distribution adopted to suppress secondary flow in the diffuser by GOTO, et al[18]
The next question is how to set the loading type (i.e.,fore-loaded, mid-loaded or aft-loaded). In terms of efficiency, ASHIHARA, et al[19]pointed out that an axial pump impeller with fore-loading shows higher efficiency than that of an axial pump impeller with aft-loading, which was validated in the parametric study of the 3D inverse design of pump inducers. Also, in the design of water-jet pumps by BONAIUTI, et al[17], the parametric study of blade loading shows that the mid-loaded blade loading had higher efficiency than that for the aft-loaded. On the other hand, the cavitation performance cannot be ignored.Through suction performance analysis, BONAIUTI, et al[17]concluded that the aft-loading type will be superior when suppressing cavitation, which is also the situation in the inverse design of the Francis runner[16]. In the case of the controlling shock losses in transonic/supersonic flow in an aerodynamic rotor, TIOW, et al[8], concluded that the mid-type blade loading will help suppress the strong shock formation near the tip.
In summary, the choice of blade loading is the balancing of efficiency and cavitation/shock. If cavitation is emphasized, the better choice is aft-loaded, otherwise, the fore-loaded or mid-loaded is preferable to improve the efficiency.
Besides setting the gradient ofthe other parameters relevant to the blade are the boundary conditions at the leading and trailing edges. Generally, the value ofat the leading edge depends on the expected angle of attack. A positive value corresponds to a positive angle of attack,implying better cavitation performance under large flow rates, and vice versa. In 3D inverse design, this manipulation is easily implemented. Especially, in the design of a high mixed flow pump and axial flow pump, a combination of different values at the leading edge from the hub to the shroud (i.e., a positive value on the shroud where cavitation easily originates and a negative value on the hub)is valid to improve the suction performance in the authors’experience. The setting ofon the trailing edge depends on the needed Euler work and the vortex type (i.e.,free vortex, forced vortex or compound vortex like Rankie vortex). In general, a free vortex is applied in cases with low and medium specific speed machines, such as centrifugal and mixed flow pumps. For higher specific speeds, the manufacturing of blades needs to be considered.Taking the axial flow pump for example, the blade near the hub side will be tuned seriously if the same Euler work as the shroud is produced. In this sense, a forced Euler work distribution is desirable. Moreover, the vortex type is related directly to the noise as far as the gas blower is concerned. From the inverse design of a propeller fan by OKAMOTO, et al[20], it was validated that a compound vortex will help reduce the noise level.
5 Stacking Condition Consideration
The stacking condition that introduces a spanwise blade force is also an important input parameter in the 3D inverse design. It functions in the same way as the blade leaning in a conventional design. However, as mentioned by ZANGENEH, et al[5], compared to blade leaning in a traditional design, the computed blade angle will change to give the correct Euler work in a 3D inverse design, which can be taken as one advantage of the inverse method. The principle of how the stacking condition redistributes the blade loading is that the blade force will change the spanwise blade loading in that the relative velocity wblwill decrease at the high pressure wall so that the blade loading will be reduced according to Eq. (10). However, design practices proved that the set must be reasonable for both aero-hydro dynamics and manufacturing. In the parametric study of a Francis turbine runner conducted by DANESHKAH, et al[16], three stacking conditions (−15°,−30°, −45°) were tested to investigate its effect on the blade pressure distribution. The two-phase flow simulation to estimate the cavitation performance shows that the blade with the −30° stacking condition had the best cavitation performance. Also, in a parametric study of a propeller fan by OKAMOTO, et al[20], it was determined that the stacking condition had an effect on the noise level, which was directly related to the pressure fluctuation. Here, this phenomenon was again validated by the conclusion drawn by GOTO, et al[4]that a suitable stacking condition will eliminate or suppress the “jet-wake” flow pattern and make the exit flow more uniform. The generated noise level is reduced by the uniformity, which suggests the pressure fluctuation is decreasing. For the propeller fan, the parametric study suggested that the stacking should be set at moderate valuesMoreover, the stacking condition can make the high efficiency and stable operating zone broader. As a typical example, the X-shaped blade applied in the Francis turbine invented by BREKKE[21], actually stacked at the leading edge, the same as the Francis runner by DANESHKAH, et al[16], and can be applied to broaden the operating range. From the point of view of manufacturing, the value of the stacking condition is subjected to the machine size and the aspect ratio of the meridional shape (i.e., large aspect ratio means low specific speed machines). The amount that is assigned to stacking adjustments needs to be enlarged in machines designed with larger sizes and higher specific speeds.
6 Combination of 3D Inverse Design and Optimization
With the development of modern turbine design, the multi-objective and multi-point optimization design is gradually being adopted by large companies. The traditional approach is automating the conventional design process by coupling an optimization method, CAD based blade generators and a computational fluid dynamics CFD code. As is pointed out by BONAIUTI, et al[22],optimization based on geometry parameters is very time-consuming with high computational cost because of the large number of parameters and the shape of the objective function to be optimized. As an effective alternative, the coupling of a 3D inverse design method with optimization techniques shows great advantages and has already been applied by several researchers(BONAIUTI, et al[22], LEE, et al[23], LU, et al[24], HE, et al[25]). The main procedure is briefly introduced as follows:the blade is first represented by the inverse design parameters (i.e., the blade loading, the spanwise circulation distribution and the stacking condition). Fig. 9 illustrates the controlling points for the blade loading distribution,where the profile can be manipulated by two points, NC and ND, and the slope, SLOPE, between them, while the incident angle can be set by the bounded value, DRVT.Subsequently, using a screening DOE (design of experiment), the parameters that are sensible responses to the performance are determined. Then, RSM (response surface methodology[26–27]) or ANN (Artificial Neural Network[28]) is adopted to establish the relationship between the design parameters and objective performance.As an example, Fig. 10 demonstrates how the blade loading and stacking conditions clearly affect the optimization objective.

Fig. 9. Blade loading parametrization

Fig. 10. Main effect of blade loading and stacking parameters on the peak and stall efficiencies, denoted by△η in Ref. [22]
Up to this point, the optimal set of parameters can be determined by multi-objective evolutionary algorithms,such as multi-objective genetic algorithm[29–30]. The above systemic optimal design methodology is advanced in that the optimization algorithms are applied to the RSM models with negligible computational cost and the optimization model, such as RSM. This can enable the designers to have knowledge about how each parameter affects the objective function and define the design rules of universal validity,which can be exploited for similar design problems.
7 Conclusions
(1) In the 3D inverse design theory, the secondary flow can be related to the equivalent pressure gradient, which can be related the design variable, i.e., the blade loading distribution.
(2) To suppress the occurrence of the secondary flow, the set of blade loading distribution should depend on the curvature of the meridional passage. Specifically, more weight of blade loading should be placed on the more curved streamlines. Usually, for centrifugal pump in which the curvature of the shroud is larger than that of the hub,under such circumstances, the shroud is more loaded.
(3) As an auxiliary alternative, the stacking parameter plays an important role to control secondary flow in that suitable stacking can improve the blade pressure distribution and decrease the non-uniformity, thus contributes to the better performance of pressure fluctuation and hydrodynamic noise.
(4) It is a perfect integration to combine the 3D inverse design with modern optimization methodologies in that both the design method and optimization technique are based on the concept of “know-how”, so that designers can have a command of the flow physics and its physical relations with the design variables. Thus, the future design system should integrate 3D inverse design, 3D CAD, CFD and optimization algorithm together.
[1] HAWTHORNE W R, WANG C, TAN C S, et al. Theory of blade design for large deflections: Part I-Two-dimensional cascade[J]. J.Eng. Gas Turbines and Power, 1983, 106: 346–353.
[2] TAN C S, HAWTHORNE W R, MCCUNE J E, WANG C. Theory of blade design for large deflections: Part II-Annular cascades[J]. J.Eng. Gas Turbines and Power, 1983, 106: 354–365.
[3] BORGES J E. A three-dimensional inverse method for turbomachinery: Part 1—Theory[J]. ASME J Turbomachinery, 1990, 11:346–354.
[4] ZANGENEH M, GOTO A, HARADA H. On the design criteria for suppression of secondary flows in centrifugal and mixed flow impellers [J]. Journal of Turbomachinery-Transactions of the ASME,1998, 120(4): 723–735.
[5] ZANGENEH M, GOTO A, HARADA H. On the role of three-dimensional inverse design methods in turbomachinery shape optimization[J]. Proceedings of the Institution of Mechanical Engineers. Part C, Journal of Mechanical Engineering Science,1999, 213(1): 27–42.
[6] KOINI G N, SARAKINOS S S, NIKOLOS I K. A software tool for parametric design of turbomachinery blades[J]. Advances in Engineering Softwawre, 2009, 40(1): 41–51.
[7] WU J C, SHIMMEI K, TANI K, et al. CFD-based design optimization for hydro turbines[J]. Journal of Fluids Engineering-Transactions of the ASME , 2007, 129(2): 159–168.
[8] TIOW W T, ZANGENEH M. Application of a three-dimensional viscous transonic inverse method to NASA rotor 67[J]. Proceedings of the Institution of Mechanical Engineers. Part A, Journal of Power and Energy, 2002, 216(A3): 243–255.
[9] WESTRA R W. Inverse-design and optimization methods for centrifugal pump impellers[D]. Enschede, The Netherlands:University of Twente, 2008.
[10] ZANGENEH M. Advanced design software for pumps[J]. World Pumps, 2007, 2007(489): 28–31.
[11] GOTO A, NOHMI M, SAKURAI T, et al. Hydrodynamic design system for pumps based on 3-D CAD, CFD, and inverse design method[J]. Journal of Fluids Engineering-Transactions of the ASME, 2002, 124(2): 329–335.
[12] ZANGENEH M, DAWES W N, HAWTHORNE W R. Three dimensional flow in radial-inflow turbines[C]//33rd ASME International Gas Turbine Conference, Amsterdam, Netherlands,1988.
[13] JIANG X, DAI R. Aerodynamic design and numerical analysis of centrifugal impeller blades[J]. Journal of Engineering Thermophysics, 2005, 26(5): 782–784.
[14] WATANABE H, OKAMOTO H, GUO S, et al. Optimization of microturbine aerodynamics using CFD, inverse design and FEM structural analysis[G]. ASME Paper GT-2004-53583, 2004.
[15] KERSCHBERGER P, GEHRER A. Hydraulic development of high specific-speed pump-turbines by means of an inverse design method,numerical flow-simulation (CFD) and model testing[C]//25th IAHR Symposium on Hydraulic Machinery and Systems, Timisoara,Romania, Sep. 20–24, 2010.
[16] DANESHKAH K, ZANGENEH M. Parametric design of a Francis turbine runner by means of a three-dimensional inverse design method[C]//25th IAHR Symposium on Hydraulic Machinery and Systems, Timisoara, Romania, Sep. 20–24, 2010.
[17] BONAIUTI D, ZANGENEH M, AARTOJARVI R, et al. Parametric design of a waterjet pump by means of inverse design, CFD calculations and experimental analyses[J]. Journal of Fluids Engineering-Transactions of the ASME, 2010, 132:031104.1–031104.15.
[18] GOTO A, ZANGENEH M, GOTO A, et al. Hydrodynamic design of pump diffuser using inverse design method and CFD;Hydrodynamic design system for pumps based on 3-D CAD, CFD,and inverse design method[J]. Journal of fluids engineering-transactions of the ASME, 2002, 124(2): 319–329.
[19] ASHIHARA K, GOTO A. Effects of blade loading on pump inducer performance and flow fields[C]//ASME 2002 Fluids Engineering Division Summer Meeting, Montreal, Quebec, Canada, July 14–18,2002:1–8.
[20] OKAMOTO H, GOTO A, FURUKAWA M. Design of a propeller fan using 3-D Inverse Design Method and CFD for high efficiency and low aerodynamic noise[C]//Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, Vail, Colorado USA,August 2–6, 2009: 1–8.
[21] BREKKE H. State of the art in turbine design[C]//Proceedings of the XXIX IAHR Congress 21 Century: New Era for Hydraulic Research and Its Application, Beijing, China, 2001: 544–551.
[22] BONAIUTI D, ZANGENEH M. On the coupling of inverse design and optimization techniques for the multiobjective, multipoint design of turbomachinery blades[J]. Journal of Turbomachinery-Transactions of the ASME, 2009, 131: 021014.1–021014.15.
[23] LEE K Y, CHOI Y S, KIM Y L, et al. Design of axial fan using inverse design method[J]. Journal of Mechanical Science and Technology, 2008, 22(10): 1883–1888.
[24] LU J, XI G, QI D. Blade optimization of mixed-flow pump by using inverse design method and neural network[J]. Journal of Xi'an Jiaotong University, 2004, 38(3): 308–312.
[25] HE L, SHAN P. Three-dimensional aerodynamic optimization for axial-flow compressors based on the inverse design and the aerodynamic parameters[J]. Journal of Turbomachinery-Transactions of the ASME, 2012, 134: 031004.1–031004.13.
[26] AHN J, KIM H J, LEE D H, et al. Response surface method for airfoil design in transonic flow[J]. Journal of Aircraft, 2001, 38(2):231–238.
[27] MYERS R H, MONTGOMERY D C. Response surface methodology: Process and product optimization using designed experiments[M]. New York: Wiley, 1995: 1–78.
[28] PIERRET S, VAN DEN BRAEMBUSSCHE R A. Turbomachinery blade design using a Navier-Stokes solver and Artificial Neural Network[J]. Journal of Turbomachinery, 1999, 121(2): 326–332.
[29] DERAKHSHAN S, MOHAMMADI B, NOURBAKHSH A. The comparison of incomplete sensitivities and Genetic algorithms applications in 3D radial turbomachinery blade optimization[J].Computers & Fluids, 2010, 39(10): 2022–2029.
[30] SAMAD A, KIM K Y. Shape optimization of an axial compressor blade by multi-objective genetic algorithm[J]. Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power And Energy, 2008, 222(A6): 599–611.
 Chinese Journal of Mechanical Engineering2014年3期
Chinese Journal of Mechanical Engineering2014年3期
- Chinese Journal of Mechanical Engineering的其它文章
- Theoretical Analysis and Experimental Verification on Valve-less Piezoelectric Pump with Hemisphere-segment Bluff-body
- Carbody Structural Lightweighting Based on Implicit Parameterized Model
- Prediction-based Manufacturing Center Self-adaptive Demand Side Energy Optimization in Cyber Physical Systems
- Effectiveness of a Passive-active Vibration Isolation System with Actuator Constraints
- Numerical Simulation and Analysis of Power Consumption and Metzner-Otto Constant for Impeller of 6PBT
- Proceeding of Human Exoskeleton Technology and Discussions on Future Research
