Theoretical Analysis and Experimental Verification on Valve-less Piezoelectric Pump with Hemisphere-segment Bluff-body

JI Jing , ZHANG Jianhui , XIA Qixiao, WANG Shouyin, HUANG Jun and ZHAO Chunsheng

1 State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

2 College of Mechanical and Electrical Engineering, Qingdao Agricultural University, Qingdao 266109, China

3 College of Mechanical and Electronic Engineer, Beijing Union University, Beijing 100020, China

4 Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

1 Introduction

As a new type of fluid actuator, piezoelectric pump is also a pioneer and concept product in the field of microminiature pump. Comparing with the traditional pump, it doesn’t need additional actuators. Based on the inverse piezoelectric effect of piezoelectric ceramics,piezoelectric pump deforms the piezoelectric vibrator and fluctuates the chamber volume to transform fluid.

Piezoelectric pump has a special type of flow resistance structure which generates different resistance of forward and reverse flow in order to achieve unidirectional flow.Piezoelectric pump has the advantages of simple structure,easy microminiaturization, low energy consumption, and no electromagnetic noise. Because there is no moving part in the chamber, the service life and reliability of the pump can be guaranteed. Furthermore, the simple structure makes the pump easy for MEMS process. As a result, piezoelectric pumps have great potential applications in the fields of biology, medical treatment[1–2], chemical industry[2], and fuel supply[3]for micro institutions.

Since piezoelectric pump was first presented by STEMME[4], different types of pumps have been put forward[5–21]. Foreign scholar OLSSON, et al[5]invented the first valve-less piezoelectric pump made on a Silicon plate.MATUMOTO, et al[6–7], put forward a type of piezoelectric pump depending on liquid viscosity varying with its temperature. Based on double-loop-pipe valve[8](also called Tesla valve), FORSTER, et al[9]designed a shaped tube valve-less piezoelectric pump, which can transport macromolecule with suspended particles and living cells.By imitating the swing of caudal-fin, PIRESA, et al[10]from Brazil developed their research on bionic piezoelectric pump which increases the flow rate effectively.

In China, some researchers have made intensive study on valve-less piezoelectric pump. CHENG, et al[11–12], found that the change of taper’s angle would affect flow rate and pressure. KAN, et al[13–14], developed the miniature piezoelectric pump for medicine transportation, and carried out the research of pump’s output performance influenced by damp on fluid. XIA, et al[15–16], presented a valve-less piezoelectric pump with hackle chamber. The corrugated design of the chamber bottom of the pump enables it to transport, mix and stir fluid. WU, et al[17], designed the valve-less piezoelectric pump with flat-cone-shape chamber and the experiment proved the pump’s preferable output performance. In recent years, ZHANG, et al[18–21],made substantial research work on piezoelectric pumps.

All above domestic and international experts and scholars have designed various kinds of piezoelectric pumps based on different principles from different point of view, which has laid the foundation for further research and development of piezoelectric pumps. However, with the development of informatization and micromachining technology, the research on valve-less piezoelectric pump should not be limited to the function of fluid pumping,instead, the control of output flow, structure for micromachining and simple technology should also be concerned. Nowadays, big flow (or micro flow) output,structure size miniaturization, low energy consumption and process simplification and so on, are the main problems pressing for solution.

This paper presents a novel valve-less piezoelectric pump with HSBB based on the method that the flow resistance on different shaped surfaces on bluff-bodies is different. This pump not only omits the traditional no-moving part valve outside the chamber, but also simplifies the inner structure of the chamber and manufacturing process, and enhances the pump’s output performance at the same time. Several HSBB with different shaped surface have been arranged in the chamber along the flow direction. Because the resistance on the spherical surface and the round surface along the flow direction is different, the actual flow resistance difference is formed in the chamber. Therefore, the unidirectional fluid pumping is obtained. Research work will be carried out on the proposed pump as follows: analyze the working process,deduce the flow rate formula which expresses the working principle of the pump, and manufacture the pump prototype and conduct experimental study on it to verify the theory and analysis.

2 Structure and Working Principle

2.1 Hemisphere-segment bluff-body

Flow resistance on objects with non-streamline shape in fluid mainly comes from frictional resistance and pressure drag. Because the surface shape of objects determines the magnitude of pressure drag, pressure drag is also called shape resistance. Table 1 shows the resistance coefficient CDof several ternary objects with typical characteristic. As we can see from the table, when Reynolds number Re=104–105, the sphere and the hemisphere with smooth surface are subjected to smaller pressure drag and lower resistance coefficient. However, typical surface like round surface with vertical end face, square surface or sharp angle points suffers bigger pressure drag and higher resistance coefficient.

Table 1. Pressure coefficient of ternary object with typical characteristic

Fig. 1 represents the structure scheme of HSBB (1/4 sphere). The hemisphere-segment is produced by cutting a sphere along the plane which contains two mutually perpendicular diameters of the sphere. This kind of object has complex geometrical surface characteristics, i.e.smooth round surface (1/4 sphere surface), vertical end face (1/2 round surface) and sharp angle points (endpoints of the diameter).

Fig. 1. Structure scheme of HSBB

When fluid comes from forward and reverse direction,the sphere surface and the round surface suffers different resistance: the resistance on the sphere surface is far less than the other one. Therefore, the HSBB can make different forward and reverse flow resistance. Aiming to achieve bigger absolute difference between forward and reverse flow resistance, and to make the fluid volume through two sides of the hemisphere-segment different in turn, the HSBB is designed as the valve of the pump to control the flow direction. Working as the no-moving part valve, the hemisphere-segment leads to no valve in the valve-less piezoelectric pump.

2.2 Structure of valve-less piezoelectric pump with HSBB

Fig. 2 shows the structure diagram of the valve-less piezoelectric pump with HSBB. The pump mainly consists of bimorph piezoelectric vibrator, pump chamber, pump seat and hemisphere-segment. The hemisphere-segments are inlaid in the groove through inserting rods on the base.Six hemisphere-segments are equally arranged in the chamber at the distance of the sphere’s diameter. One of the two flow-facing sides of the hemisphere-segment, the orifice faced directly by 1/4 spherical surface, is the entrance of the pump. And the other orifice faced directly by 1/2 round surface is the export. The pressure drag on the smooth spherical surface facing the entrance is smaller than another one, which forms the flow resistance difference. When the pump is working, the flow rate of inspiratory fluid from the entrance is more than that from the export. And the flow rate of discharged fluid through the export is more than that from the entrance. Hence the unidirectional flow is formed in one work cycle of the pump. The pump makes ingenious use of the hemisphere-segment’s characteristic that flow resistance on different geometrical shape at flow-facing side is different.And then the flow resistance difference between forward and reverse direction is formed, which plays the function of fluid pumping.

Fig. 2. Structure of valve-less piezoelectric pump with HSBB

In principle, object of any type of shape with asymmetric structure in forward and reverse flow direction in the pump chamber, can work as the no-moving part valve. Because hemisphere-segment has the advantages of simple process,stable forward and reverse flow resistance, this paper chooses it as the bluff-body for the valve-less piezoelectric pump. Comparing with traditional valve-less piezoelectric pump, valve-lee piezoelectric pump with HSBB leaves out the complex pipeline structure outside the chamber, as well as brings about the advantages of simple process, compact structure and convenient adjustment of the interior pump chamber.

2.3 Principle analysis of valve-less piezoelectric pump with HSBB

The flow resistance on the bluff-body is sum of frictional resistance and pressure drag. However, it is theoretically extremely difficult to solve the resistance on arbitrary shape objects. Taking the hemisphere in the chamber as research object, basing on force analysis of bluff-body, the forming reason and size and action law of flow resistance are analyzed. The unidirectional fluid pumping of the pump is theoretically explained as follows.

Flow from 1/4 spherical surface of hemisphere-segment(flow-facing side) to 1/2 round surface of hemispheresegment (flow-dorsal side) is defined as the forward flow.Conversely we can get the reverse flow. Fig. 3 gives the schematic diagram of the flow resistance on the flow-facing side and flow-dorsal side at the two flow direction above.

Fig. 3. Force diagram of hemisphere-segment at forward and reverse flow

As shown in Fig. 3, the force on the hemisphere-segment can be divided into friction resistance (Ff) caused by fluid viscosity, static pressure on flow-facing side (pY), reverse pressure on flow-dorsal side (FB) and reacting force to the disturbance around (FN). Among them, FBis the pressure towards the flow-dorsal surface of the object caused by tail fluid driven by surrounding fluid. The direction of FBis opposite to the flow direction.

Hence, when fluid comes from forward and reverse direction, the total force FDon flow-facing and flow-dorsal surface of hemisphere-segment along the horizontal flow direction is

where, the vertical fiction on the flow-facing side of round surface in Fig. 3(b) is ignored here. Essentially, pY, FBand FNare affected by flow pressure directly or indirectly.Their comprehensive effect leads to pressure loss when fluid flows through hemisphere-segment and ultimately represented as pressure drag and shape resistance. It is in accordance with the fluid flow theory[22–23]that flow resistance on objects is the sum of friction resistance and pressure drag when fluid flows around.

Owing to the complexity and uncertainty of flow field movement, the size and action law of pBand FNis much more complicated than friction force. Based on mathematics and physics, the flow resistance on hemisphere-segment against forward and reverse flow is analyzed qualitatively and compared as follows.

2.3.1 Analysis of reverse pressure on flow-dorsal side

The pressure within enclosed space relates to not only the capacity of the enclosed space, but also the fluid volume inflowing the space. When the capacity of the enclosed space is constant, the pressure increases along with the increasing of fluid volume inflowing the space.

Suppose that inflow flows horizontally through the static hemisphere-segment from left to right at the uniform velocity of U. Due to the relativization of motion, the hemisphere-segment can be regarded as moving horizontally from right to left in static fluid at the uniform velocity of U.

As shown in Fig. 4, when the hemisphere-segment moves a micro distance ΔS towards left front during time Δt,namely both 1/4 spherical surface and 1/2 round surface moves from location AB to A′B′.

Fig. 4. Analysis of reverse pressure at forward and reverse flow

Then 1/4 spherical surface drains out the fluid at the volume of sphere space A′DECB′E′A′ shown in Fig. 4(a).And the lateral terminal of hemisphere-segment, that is the round flow-dorsal side, vacates a space at the volume VZHof half cylinder ABB′A′A. In Fig. 4(b), 1/2 round surface drains fluid out at the volume of half cylinder ABB′A′A, and outside of the end of hemisphere-segment, 1/4 spherical flow-dorsal side, vacates a space at the volume VQof sphere AEBC′E′D′A. The volume can be expressed as follows:

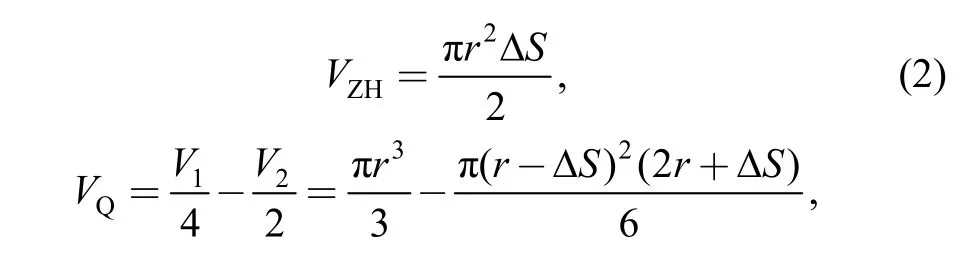
where r is sphere’s radius, V1is sphere’s volume, V2is the volume of sphere-segment D′E′C′. Clear the equation, we can obtain the equation as

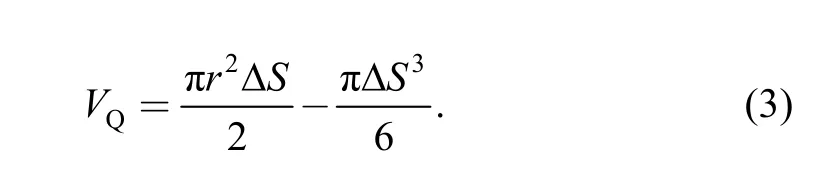
Comparing Eq. (2) with Eq. (3), when ΔS is small enough, it can be concluded that VQ≈VZH.That is, during timet, the hemisphere-segment goes forward a micro displacement ΔS, and VZHis approximately equal to VQ.

According to the above analysis, once enclosed spaces VZHand VQare formed at the wake flow, surrounding fluid will fill into space VZHand VQrapidly driven by environmental pressure and then the pressure in the space will rise again quickly. When fluid comes in forward direction, the flow-facing side is cylindrical surface, and its flow-facing area perpendicular to the flow direction is SZH=πr2/2; when fluid comes in reverse direction, the flow-facing side is 1/4 spherical surface, and its flow-facing area perpendicular to the flow direction is SQ=πr2/3. Owing to SZH＞SQ, the fluid mass filled into space VZHis larger than space VQin the same time. In addition, because VQ≈VZH, the pressure in VZHis also larger than VQ.

Based on the above analysis, it is found that reverse thrust on 1/2 round surface in forward flow is larger than on 1/4 sphere surface in reverse flow.

2.3.2 Analysis of disturbing force on flow-facing side

When object moves in fluid, the resistance caused by its forepart movement is much more complex than that caused by its tail shape. The front resistance is produced by static pressure and the strong disturbance (also can be called thrust force) on front fluid caused by advancing forepart.Distancing force was once described by Newton[24]as follows: object shall drain fluid out at the mass of M=ρAU per second along the way. In this process, each fluid element has its own velocity which is thought to be proportional to the macro velocity. Moreover, the resistance is equal to the momentum applied on fluid per second.Hence, fluid element velocity is proportional to MU=ρAU2.Where, ρ is fluid dense, U is kinematic velocity of the object, A is area of face-facing surface.

In order to calculate the resistance caused by fluid disturbance, every fluid element velocity needs statistic. It is extremely difficult. With mathematics comparison method, possible disturbance quantities caused by 1/4 sphere face-facing surface in forward flow and by 1/2 round face-facing surface in reverse flow are analyzed respectively.

For the convenience of analysis, mirror the hemisphere-segment along a half round surface and a hemisphere is obtained. At this time, the areas of the flow-facing side in forward and reverse flow are both doubled, which has no influence on the analysis result.

The velocity direction on flow-facing side in forward and reverse flow is shown in Fig. 5. In Fig. 5(a), the 1/2 round surface is the section crossing the center of hemisphere. Let θ be the angle between a horizontal line crossing any point on the round and the tangent crossing this point. When fluid comes in forward direction, decompose horizontal velocity U applied on the hemisphere surface, and the normal velocity Usinθ can be obtained; When fluid comes in reverse direction, the velocity U applied on the round surface is vertical to the round face pointing in as shown in Fig. 5(b).

Fig. 5. Velocity direction on face-facing surface in forward and reverse flow

Based on above analysis, the fluid element velocity in forward flow is equal to 1/sinθ of that in reverse flow. That is, the deflection on surrounding fluid caused by sphere surface is 1/sinθ of that caused by round surface.

According to Newton flow resistance theory, the disturbance quantity MUQon sphere face-facing surface can be calculated. In Fig. 6, spherical center is the origin of the polar coordinate system, θ is polar angle, and r is pole diameter.

Fig. 6. Hemisphere surface integral

Spherical surface integral can be seen as the integral over θ on the spherical surface encircled by arc length dS.Calculation is as follows:

That is,

Disturbance quantity MUYis

Comparing Eq. (4) and Eq. (5), it can be concluded that disturbance quantity on hemispherical face-facing surface in forward flow is smaller than that on round face-facing surface in reverse flow.

According to above analysis, through comparison of fluid volume drained out by flow-dorsal surface and disturbance quantity caused by face-facing surface, reverse pressure size and disturbing force size of pressure drag are discussed in detail. This kind of qualitative analysis of force size on bluff-body in pump chamber is named Volume and Momentum Comparison Method here.

Based on above analysis, it is found that: without considering other influences, the flow resistance on 1/4 spherical face-facing surface in forward flow is far less than that on 1/2 round face-facing surface in reverse flow.

2.3.3 Analysis of friction force and normal pressure

This part analyses the relationship between friction force and normal pressure on spherical and round surface in forward and reverse flow. In forward flow, friction force and normal pressure is applied on the face-facing surface simultaneously, and friction force is so small as can be ignored. In reverse flow, friction force on face-facing surface has no component in horizontal direction. Hence,there is only normal pressure applying on face-facing surface.

In Fig. 7, let p be the pressure on face-facing surface and θ is the same as that in Fig. 5. Then the distributed normal pressure on 1/4 spherical and 1/2 round surface can be approximated as follows:

Fig. 7. Friction force and normal pressure on face-facing surface in forward and reverse flow

Comparing Eq. (6) and Eq. (7), it can be concluded that normal pressure pQon spherical surface in forward flow is less than normal pressure pyon round surface in reverse flow.

On the basis of the above analysis, considering Eq. (1),the flow resistance on HSBB in forward and reverse flow is different. Resistance FD1on spherical face-facing surface in forward flow is far less than resistance FD2on round face-facing surface in reverse flow.

The dimensionless definition formula of flow resistance coefficient is

where CD—Flow resistance coefficient,

A—Projected area perpendicular to flow direction,

U—Flow velocity.

As for the above hemisphere-segment, the projected area of the two face-facing surface is equal. Because FD1＜FD2,there is CD1＜CD2.

In conclusion, the resistance on spherical and round surface is different when fluid flows through, and the former is far less than the latter. That is, flow resistance coefficient on spherical surface is far less than that on round surface. Therefore, when fluid flows into pump chamber through pipe orifices, the fluid volume inflowing from left entrance is far more than from right entrance. And the drained fluid volume through right exit is far more than through left exit in drainage process. The function of unidirectional fluid pumping for this valve-less piezoelectric pump is thus achieved.

2.4 Working process analysis of valve-less piezoelectric pump with HSBB

Based on the reciprocating vibration of piezoelectric vibrator, a working cycle of piezoelectric pump can be divided into four stages shown in Fig. 8.

Fig. 8. Vibration cycle of piezoelectric vibrator

In Fig. 8, W is amplitude of the piezoelectric vibrator,abscissa t is vibration time, and T is one working cycle of the piezoelectric. Let the vibrator vibrate upward from horizontal position t=0 to maximum displacement position t=T/4 be the first working stage; downward from maximum displacement position to horizontal position t=T/2 be the second working stage; downward from horizontal position to reverse maximum displacement position t=3T/4 be the third working stage; upward from reverse maximum displacement position to horizontal position t=T be the last stage. Therefore, this type of reciprocating vibration forms the reciprocating absorbing and drainage process of the pump.

In absorbing process (the first and last stage) shown in Fig. 9(a), the vibrator vibrates upward, which uplifts the vibrator surface, increases the chamber volume, and decreases the pressure in the chamber which is lower than the atmospheric pressure at pipe orifices. Fluid is absorbed into the chamber from left entrance and right exit simultaneously. Because the resistance on spherical surface of hemisphere-segment is far less than on round surface in the chamber, the fluid volume absorbed from left entrance is more than from right exit.

In draining process (the second and third stage) shown in Fig. 9(b), the vibrator vibrates downward, which recesses the vibrator surface, decreases the chamber volume, and increases the pressure in the chamber which is higher than the atmospheric pressure at pipe orifices. Fluid is drained out through left entrance and right exit. In the same way,because the resistance on spherical surface of hemisphere-segment is far less than on round surface in the chamber, the fluid volume drained out through right exit is more than through left entrance. Hence, in a cycle of vibration, a full working process of absorbing and draining process is achieved. The reciprocating vibration leads to the unidirectional fluid pumping in the chamber.

Fig. 9. Schematic diagram of working process

3 Analysis of Pump Flow

As shown in Fig. 10(a), in absorbing process, fluid flows into the pump chamber from left entrance and right exit.And it can be found that fluid velocity and pressure have changed after flowing through spherical and round surface of hemisphere-segment. Let v11, p11and v12, p12be the average velocity and average pressure of fluid entering from left entrance at left entrance and right exit section A1-A1, respectively. Let v21, p21and v22, p22be the average velocity and average pressure of fluid entering from right exit at right exit and left entrance section A2-A2,respectively. Draining process is shown in Fig. 10(b). Fluid is drained out of the chamber through left entrance and right exit. In the same way, let v11′, p11′ and v12′, p12′be the average velocity and average pressure of fluid drained out through left entrance at left entrance and right exit section A1-A1, respectively. Let v2′1, p2′1and v2′2, p2′2be the average velocity and average pressure of fluid drained out through right exit at right exit and left entrance section A2-A2, respectively.

Fig. 10. Analysis of pump flow at entrance and exit

Bernoulli Equation and Continuity Equation are allowed at left entrance, right exit and section A1-A1and A2-A2. The Bernoulli Eq. (9) (after arrangement) and Continuity Equation are as follows:

where p11, p21is the pressure at left and right pipe orifices in absorbing process. p11′, p2′1is the pressure at left and right pipe orifices in draining process. p11′and p2′1are both considered as relative atmospheric pressure, which can be dismissed comparing with the average pressure in the chamber. CD1is the resistance coefficient when coming fluid flows through the entire 1/4 spherical surface of hemisphere-segment. CD2is the resistance coefficient when coming fluid flows through the entire 1/2 round surface of hemisphere-segment. A0is the sectional area of pipe orifice.A is the sectional area of pump chamber.

In fluid absorbing (or draining) process, let ΔV be the chamber volume fluctuation caused by upward (or downward) vibration of vibrator. Dismissing the influence of bubbles, etc, on pump flow, it can be considered that chamber volume fluctuation is equal to the volume of absorbed (or drained) fluid, which is as follows:

where Q11is the fluid volume absorbed from left entrance;Q21is the fluid volume absorbed from right exit; Q11′ is the fluid volume drained out through left entrance; Q21′ is the fluid volume drained out through right exit.

Because the fluid volume absorbed from left entrance is equal to the fluid volume drained out through right exit,and the fluid volume absorbed from right exit is equal to the fluid volume drained out through left entrance, we can get

In a working cycle, the pump flow can be expressed as the flow difference at any one of two pipe orifices when fluid flows in and out. Take the left entrance for example:

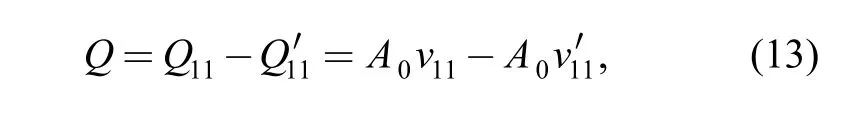
where v11, v11′ are the average velocity of fluid at the left entrance in absorbing and draining process. According to the conclusion that the resistance in forward flow is far less than in reverse flow, v11andiv′ is obtained ignoring that fluid is absorbed from and drained through the right exit at the same time. Substitute Eq. (9), Eq. (10), Eq. (11) and Eq. (12) into Eq. (13), Eq. (14) can be obtained after arrangement:

The net flow in a vibration cycle can be obtained from Eq. (14). Let the working frequency of vibrator be f, the pump flow per unit time QLcan be expressed by Eq. (15).

where w(r, T/4) is the vibration amplitude of each point on the vibrator in each process; R is the vibrator radius; w0is the vibration amplitude of the center point of the vibrator.

According to the above analysis, it is known that CD1＜CD2, hence we can get:

That is, in a working cycle, fluid volume absorbed from the entrance is greater than drained out through the entrance. In the same way, fluid volume absorbed from the exit is greater than it is absorbed from the exit. As a result,fluid flows into the chamber and flows out of the chamber.While the vibrator reciprocates at a certain frequency f, the ordered unidirectional fluid pumping is formed in the chamber. That is, the valve-less piezoelectric pump with HSBB implements the function of pumping fluid.Meanwhile, the greater the difference between resistance coefficient CD1and CD2when fluid flows through the hemisphere-segment in forward and reverse direction simultaneously is, the stronger the pumping ability is. Six hemisphere-segments are closely fixed on the pump base in the experiment. It makes resistance coefficient decrease in forward flow, resistance coefficient increase in reverse flow,which leads to a greater flow resistance difference.

The value of resistance coefficient CD1and CD2is hard to solve by analysis, when theoretical flow is calculated by Eq. (15). Thus, this paper measures the value through experiments.

4 Experiment Research

4.1 Performance experiment of fluid pumping

As shown in Fig. 11 it is the pump prototype for the experiment. Fig. 11(a) shows the pump base. There processed a vertical channel groove for fixing hemisphere-segment on it. Six hemisphere-segments are fixed in the channel groove uniformly at the distance of spherical diameter. What’s more, the spherical surface faces the pump entrance, and the half round surface faces the pump exit. Fig. 11(b) shows the assembled prototype of the proposed pump. The pump body is manufactured of organic glass. The hemisphere-segment is obtained from steel ball by wire cutting. Clearance fit is used between pump chamber and pump base, and the joint surface is sealed by O-type seal ring. The geometrical parameter of the prototype is given in Table 2.

Fig. 11. Pump base and prototype of the proposed pump

Table 2. Geometrical parameter of the prototype

Water is chosen as working fluid in the experiment.Pump flow and the relationship between pressure difference and working frequency and working voltage are measured respectively in the experiment. The results are shown in Figs. 12–15.

Fig. 12. Relationship between pump flow and voltage

Fig. 13. Relationship between pump flow and frequency

Fig. 14. Relationship between pressure difference and voltage

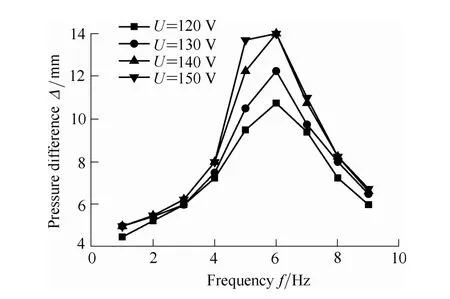
Fig. 15. Relationship between pressure difference and frequency

As shown in Fig. 12, pump flow increases as the voltage applied on the vibrator is increased. When the voltage is increased to 160 V at the frequency of 6 Hz, the pump flow reaches 0.44 mL/s. Frequency has significant effect on pump flow as shown in Fig. 13. When the frequency is about 6 Hz at the voltage of 110 V, the pump flow reaches 0.50 mL/s.

As shown in Fig. 14, the pressure difference of the pump increases significantly as the voltage is increased. At the voltage of 160 V and the frequency of 6 Hz, the pressure difference reaches 26.2 mm H2O. As shown in Fig. 15,when the frequency is about 6 Hz at the voltage of 150 V,the pressure difference reaches 14 mm H2O.

4.2 Flow resistance measuring experiment

Experimental principle is shown in Fig. 16. The experimental equipment is composed of fluid storage bottle,prototype pump, cushion block and measuring glass. The measuring glass is transparent with marks of calibration on its surface. The large volume fluid storage bottle is filled with water. The height of water level is much higher than the pump height, which ensures a certain water level and a constant and stable velocity at the exit while the pump is working.

Fig. 16. Principle of flow resistance measuring

The first step of the experiment is to fill the fluid storage bottle with water, and assemble the pump according to the forward direction. Hemisphere-segments are not to be fixed in the chamber. Now turn on the switch and start the timing.When collected water reaches a specified volume (300 mL),stop the timing. After repeating the process above 3 times,exchange the entrance and the exit of the pump to make the reverse flow in the pump. Repeat the process 3 times in the same way, thus the average velocity and the energy lose can be calculated. Afterwards, fix the six hemisphere-segments in the chamber, and repeat the same measure process 3 times in forward and reverse flow respectively. After that,calculate the average velocity and the energy lose after the hemisphere-segments have been fixed. The difference between the above two energy lose is the pressure different lose Δp caused by six hemisphere-segment. Its resistance coefficient can be expressed by Eq. (8), which can be arranged as:

From Eq. (17), if pressure difference Δp and fluid average velocity U in forward and reverse flow can be calculated, the resistance coefficient CD1and CD2in forward and reverse flow can also be obtained.

Based on the experiment method above, the change curve of resistance coefficient and velocity in forward and reverse flow can be obtained after measurement as shown in Fig. 17. The resistance coefficient both increase with the increasing of velocity, which is consistent with the changing trend of typical ternary objects. Meanwhile, there exits relatively great difference between forward and reverse resistance coefficient as the velocity changes. At the velocity of 20 mm/s and 31 mm/s, reverse resistance coefficient is 2 times and 4 times larger than forward resistance coefficient. This provides sufficient theoretical basis for the valve-less piezoelectric pump with HSBB.

Fig. 17. Change curve of forward and reverse resistance coefficient and velocity

5 Comparison between Theoretical and Experimental Pump Flow Rate

The theoretical pump flow is calculated according to Eq. (15), and Eq. (16), among which vibration amplitude relates to the changing of frequency, but the frequency has less effect on vibration amplitude in low frequency. This paper calculates the chamber volume fluctuation ΔV at the frequency of 6 Hz and the vibration amplitude of w0=0.12 mm. Considering resistance coefficient CD1=0.069 and CD2=0.120 at the velocity of 20 mm/s in Fig. 17, the theoretical pump flow QLat each frequency has been calculated. The flow rate Qsat each frequency and the voltage of 110 V is taken as the experiment pump flow rate.The theoretical and experimental pump flow rate varying with the frequency is shown in Fig. 18.

Fig. 18. Curve of theoretical and experimental flow rate varying with frequency

As shown in the figure, the theoretical and experimental flow rate both increase with the increasing of the frequency.The two variation trends keep consistent within a certain frequency, which verifies the above theoretical analysis.However, there exits large deviation between theoretical and experimental flow rate: the maximum relative deviation is 87.00%, the minimum relative deviation is 45.00% and the average relative deviation is 59.96%. The reason can be conclude as follows:

(1) Because of the complexity of flowing of flow field,there is no practical flow equation for engineering application so far. For this reason, as to the analysis of flow problem, model transplantation and simplification are commonly used today. In this paper, the derived theoretical flow rate equation is based on steady flow model. However,the actual flow pattern in the experiment is transient. It is easy to produce shock wave in transient flow, and there consumes a large number of flow energy by vibration and impact of shock wave. This energy is transformed into heat irreversibly, which leads to the nonconservation of mechanical energy and the less experimental flow rate than theoretical flow rate.

(2) Within the calculation of theoretical flow rate, the value of resistance coefficient is taken at the velocity of 20 mm/s in the chamber. However, the actual velocity is far less than 20 mm/s. The lower velocity is, the less flow resistance different is, and the smaller the theoretical flow rate is. Therefore, the taken value of resistance coefficient leads to the larger theoretical flow rate.

(3) Within the calculation of theoretical flow rate, the chamber volume fluctuation at any frequency is based on the maximum amplitude of the central point of vibration,which increases the theoretical flow rate.

(4) Within the experiment, the separation of boundary layer will take place when fluid flows through the hemisphere-segment, and there occurs a large amount of vortexes near the separation. These vortexes will aggravate the impact among fluid particles, hinder the movement of flow micelles, consume the flow energy and eventually decrease the experimental flow rate.

(5) Within the experiment, because of the influence of fluid pressure in the chamber, the maximum amplitude of piezoelectric vibration in the chamber is lower than that outside the chamber. It decreases the drained fluid volume.Besides, the appearance of cavitation also decreases the pump flow rate to some extent. Furthermore, the measurement error has a big effect on the experimental flow rate.

6 Conclusions

(1) Based on the theory of flow around bluff-body, a novel valve-less piezoelectric pump with HSBB is presented. Taking advantage of the difference of flow resistance on the spherical and round surface of HSBB in the chamber, the unidirectional fluid pumping is achieved.

(2) On the basis of the comprehensive application of mathematics and physics knowledge on HSBB, the volume and momentum comparison method—a new created qualitative analysis method of the force on bluff-body in the chamber is presented. Meanwhile, it provides an effective analysis method for the qualitative analysis of the force on objects in the chamber.

(3) Combined with the related theories and analysis of fluid, the mathematical formula of pump flow rate is analyzed and deduced, and the mechanism of unidirectional fluid pumping is verified.

(4) The experiment proves the fluid pumping characteristic of this proposed pump, and the accuracy of the above theoretical analysis is verified in turn. The measured flow rate and pressure difference both reach a great value, which proves the good pumping performance of the pump.

[1] LINTEL VAN H T G, POL V D F C, BOUWSTRA S. A piezoelectric micropump based on micromachining of silicon[J].Sensors and Actuators, 1988, 15(2): 153–167.

[2] SHOJI S, NAKAGAWA S, ESASHI M. Micropump and sample-injector for integrated chemical analyzing systems[J].Sensors and Actuators A: Physical, 1990, 21(1–3): 189–192.

[3] EDERER I, RAETSCH P S, CHULLERUS W, et al.Piezoelectrically driven micropump for on-demand fuel-drop generation in an automobile heater with continuously adjustable power output[J]. Sensors and Actuators A: Physical, 1997, 62(1–3):752–755.

[4] ERIC S, GORAN S. A valve-less diffuser/nozzle-based fluid pump[J]. Sensors and Actuators A, 1993, 39(12): 159–167.

[5] OLSSON A, STEMME G, STEMME E. A valve-less planar fluid pump with two pump chambers[J]. Sensors and Actuators A, 1995,46–47: 549–556.

[6] MATSUMOTO S, KlEIN A, MAEDA R. Bi-directional micro pump based on temperature dependence of liquid viscosity[J]. Journal of Mechanical Engineering Laboratory, 1995, 53(6): 187–193.

[7] MATSUMOTO S, KLEIN A, MAEDA R. Development of bi-directional valve-less micro pump for liquid[C]//Micro Electro Mechanical Systems, 1999. MEMS'99. IEEE,Nashville, Tennessee,November 14–19, 1999: 141–146.

[8] TELSA N. Valvular conduit: US Patent,1329559[P]. 1920-02-03.

[9] FOSTER F K, BARDELL R L, BLANCHARD A P, et al.Micropumps With fixed valves: US patent 5876187[P].1999-03-02.

[10] ROGERIO F. PIRESA, SANDRO L. VATANABEB, AMAURY R.De Oliveirab, et al. Water cooling system using a piezoelectrically actuated flow pump for a medical headlight system[C]//Industrial and Commercial Applications of Smart Structures Technologies 2007, California, USA, March 19–20, 2007: 1–11.

[11] CHENG Guangming, SUZUKI K, HIROSE S, et al. A piezoelectric pump with new structure[C]//The 76th JSME Fall Annual Meeting,Senne Dai, 1998, V: 247–248.

[12] CHENG Guangming, ZENG Ping, WU Boda, et al. Relationship analysis on cone angle and pump performance of a new structure piezoelectric pump[J]. Piezoelectrics & Acoustooptics, 1999, 21(2):104–107. (in Chinese)

[13] KAN Junwu, XUAN Ming, YANG Zhigang, et al. Performance analysis and experimental research on micro piezoelectric pump for transporting medicine[J]. Journal of Biomedical Engineering, 2005,22(4): 809–813. (in Chinese)

[14] KAN Junwu, PENG Taijiang, DONG Jingshi, et al. Effect of fluid additional damping on micro-pump output performance[J]. Journal of Xi'an Jiaotong University, 2005, 39(5): 548–550. (in Chinese)

[15] XIA Qixiao, ZHANG Jianhui, LI Hong, et al. Valve-less piezoelectric pump with unsymmetrical slope chamber bottom[J].Optics and Precision Engineering, 2006, 14(4): 641–647. (in Chinese)

[16] XIA Qixiao, ZHANG Jianhui, LEI Hong, et al. Theoretical analysis of novel valve-less piezoelectric pump with cluster of unsymmetrical hump structure[J]. Optics and Precision Engineering,2008, 16(12): 2391–2397. (in Chinese)

[17] WU Liping. Theoretical and experimental research of valveless piezoelectric pump with flat-cone-shape pump chamber[D].Changchun: Jilin University, 2008. (in Chinese)

[18] ZHANG Jianhui, XIA Qixiao, LAI Dehua, et al. Discovery and analysis on cavitation in piezoelectric pumps[J]. Chinese Journal of Mechanical Engineering, 2004, 17(4): 591–594. (in Chinese)

[19] ZHANG Jianhui, LI Yili, XIA Qixiao, et al. Analysis of the pump volume flow rate and tube property of the piezoelectric valve-less pump with Y-shape tubes[J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 136–141. (in Chinese)

[20] ZHANG Jianhui, LU Jizhuang, XIA Qixiao, et al. Working principle and characteristics of valve-less piezoelectric pump with Y-shape tubes for transporting cells and macromolecule[J]. Chinese Journal of Mechanical Engineering, 2008, 44(9): 92–99. (in Chinese)

[21] HU Xiaoqi, ZHANG Jianhui, XIA Qixiao, et al. Influence from length of flexible caudal-fin for caudal-fin-type piezoelectric pump[J]. Journal of Mechanical Engineering, 2012, 48(8): 167–173.(in Chinese)

[22] DING Zurong. Hydromechanics[M]. Beijing: Higher Education Press, 2003. (in Chinese)

[23] JIANG Zhongxia, JIANG Chuantao, LIU Guifang. Vortex shedding flowmeter[M]. Beijing: China Petrochemical Press. (in Chinese)

[24] PRANDTL L. Introduction of hydromechanics[M]. GUO Yonghuai,LU Shijia, trans. Beijing: Science Press, 1981.

[25] CHENG Guangming, YANG Zhigang, ZENG Ping. Research on the cavity volume fluctuations of piezoelectric pump[J]. Piezoelectrics& Acoustooptics, 1988, 20(6): 389–392. (in Chinese)