Numerical Simulation and Analysis of Power Consumption and Metzner-Otto Constant for Impeller of 6PBT

LUAN Deyu, CHEN Qiao and ZHOU Shenjie

1 School of Mechanical and Electrical Engineering, Qingdao University of Science and Technology,Qingdao 266061, China

2 School of Mechanical Engineering, Shandong University, Jinan 250061, China

1 Introduction

Stirred tanks are widely used in chemical industries and biotechnological processes for mixing highly viscous non-Newtonian fluids[1]. Majority of these non-Newtonian fluids are pseudoplastic with shear-thinning property, and some also possess a yield stress. The rheological complexities of pseudoplastic fluids can cause a variety of difficulties, including most important changes in viscosity during processing. For example, shear-thinning fluids are viscous at the beginning, and then once the shear rate is increased the viscosity will drops dramatically, as well as being different in different parts of the mixing tank. In these situations, it is difficult to predict accurately the power consumption and mean shear rate in a stirred vessel to achieve a optimum way of economical mixing. Apparent viscosity concept proposed by Metzner and Otto[2]has been adapted widely and become a classical method of solving the power consumption for mixing of non-Newtonian fluids.The concept assumes that the mean shear rate γ˙is proportional to the rotation speed of impeller, where the proportional coefficient ksis referred to as the Metzner-Otto constant. The power curve of non-Newtonian fluids obtained using the Metzner-Otto method is consistent with that of Newtonian fluids. This explains the fact that the Metzner-Otto method is a widely used method to design impellers for non-Newtonian fluids applications[3–4]. As a result, the ksvalue has become a key factor to predict power consumption. It is readily agreed that ksis a function of impeller geometry, but there are some conflicting conclusions regarding the relationship between ksand fluid rheological index n. For instance, BECKNER, et al[5],and SAWINSKY, et al[6], concluded thatsk decreases sharply as n increases. However, CALDERBANK, et al[7], SCHILO[8]and SESTAK, et al[3], found that ksdecreases weakly as n increases. TANGUY, et al[9], and CARREAU, et al[10], reported that ksincreases slowly with the increasing n. The work of POLLARD, et al[11]and RIEGER, et al[12]showed that ksis a constant that should be insensitive to the rheological properties of the fluids in the laminar regime for any given impeller geometry. Generally, close-clearance impellers, such as anchors, helical screws or helical ribbons, are recommended for mixing highly viscous non-Newtonian fluids as the most effective mixers. However, such impellers, for example helical ribbons, are sensitive to highly shear-thinning behavior which reduces their mixing effectiveness[13].

The impeller composed of perturbed six-bent-bladed turbine (6PBT) is an improved shape on basis of six-bent-bladed turbine (6BT) with its good mixing performance and its capacity of operating over a wide viscosity range. The six bent blades are perturbed up and down, respectively, to generate the periodically changeable flow in a stirred tank and then induce the chaotic mixing of pseudoplastic fluids[14]. Therefore, the aim of this paper is to use computational fluid dynamics (CFD) as a tool to study the power consumption of the 6PBT impeller with different geometries in stirring pseudoplastic fluids possessing yield stress. The experimental power values are used to validate the CFD model. The influence of pseudoplasticity is analyzed using the classical approaches found in the literature, such as Metzner-Otto concept[2]and Rieger-Novak method[12]. This work provides the complete correlations of power constant and Metzner-Otto constant with impeller geometry. These results can be used to accurately predict the power consumption and mean shear rate of the pseudoplastic fluids in laminar flow region,comparatively.

2 Experimental Setup and Procedure

The experimental setup is shown in Fig. 1. The mixing vessel used in this work consists of a transparent cylindrical tank of diameter (T) 0.21 m. The flat-bottomed tank was fitted with four equally spaced flat baffles, each with a width (w) equal to T/10. The fluid height (H) was maintained constant at a height equal to the tank diameter.The 6PBT impeller was mounted on a centrally located shaft of diameter 0.016 m and driven by a variable-speed motor. The impeller was positioned at an off-bottomed clearance (C) of T/3 and backswept angle of blade is θ.Further details about the geometrical characteristics of the stirred tank are showed in Fig. 1. The torque and speed of the impeller were measured using a rotary-torque transducer.

A Newtonian fluid (glycerine solution) and seven types of opaque xanthan gum solutions in water at different mass concentrations ranging from 0.5 wt %–2.0 wt % were used in this work. The rheological properties of the fluids were determined by a Brookfield rheometer.

For Newtonian fluid, the viscosity is independent of the shear rate at a fixed temperature. The density ρ of glycerine solution measured is 1260 kg/m3, and its viscosity η=0.799 Pa • s. Theoretical and experimental studies[15]have shown that the power number Npis inversely proportional to the Reynolds number Re in the laminar flow:

where N is impeller speed, and D is impeller diameter.

Fig. 1. Experimental setup

The power consumption P drawn by the impeller, was computed by means of the torque

where M is the moment vector about the center of the impeller.

Then the power number Npwas calculated as follows

The xanthan gum solution is a pseudoplastic fluid with a yield stress. Thus, its rheology can be described by Herschel-Bulkley model[16-17]:

Table 1 summarizes the rheological parameters of xanthan gum solutions with seven mass concentrations based on measured data.

Table 1. Rheological parameters of xanthan gum solutions

Metzner-Otto correlation was used to obtain apparent Reynolds number for Herschel-Bulkley fluids. According to this correlation, the mean shear rate can be related to the impeller speed by

where ksis Metzner-Otto constant and it is assigned a value of 11.5 for the radial flow impeller[18],is mean shear rate.

The mean shear rate can be used to evaluate the apparent viscosity aη of the solutions using Herschel-Bulkley rheological model:

The apparent Reynolds numbercan be defined as

Metzner-Otto and Rieger-Novak methods are widely used to solve ksvalue. Metzner-Otto method defines Renand Kpnby

where Rne is Reynolds number for non-Newtonian fluids,is power constant for non-Newtonian fluids, it is a function of n, so that

The ksvalue can be directly calculated from Eq. (11)and this method is also referred to as direct calculation of

Rieger-Novak method is denoted as the slope method based on the linearized Eq. (11):

If ln Kpnhas a linear relationship with (1−n), it shows that ksis independent of the flow behavior index n. Then the ksvalue can be obtained from the slope of the straight line resulting from the plot of ln Kpnversus (1−n).

WANG, et al[19], found that when ksis independent of the flow behavior index n, the slope method which avoids exponential operation, can be applied to predict ksmore accurately than direct calculation method. Therefore,Rieger-Novak method was adopted to determine kpand ksvalue through CFD data- processing in this work.

3 CFD Simulations

Fluent V6.3 (Fluent Inc.) was used to simulate the steady-state 3D flow field in laminar regime by solving the conservation of mass and momentum equations. It utilized the steady-state multiple reference frames (MRF) technique to realistically model the rotation of the impeller in the mixing vessel. This technique has been found to yield flow field predictions comparable to those obtained using the sliding mesh (SM) model[20–21]. A pre-processor (Gambit 2.3, Fluent Inc.) was used to discretize the flow domain with a tetrahedral mesh. The domain is segmented into two zones: stator zone and rotor zone (Fig. 2). Grid independence was verified by demonstrating the additional requirement on mesh cells that did not change the calculated power number and velocity magnitude in the regions of high velocity gradients close to the impeller blades by more than 3%. The original 3D mesh of the model for calculation domain had about 342 100 cells by taking the 6PBT impeller ofas an example. The number increased to about 660 500 to verify the grid independency. This increase changed the velocity and power number in regions of high velocity gradients by more than 3%. When the number of cells further increased to 1 086 432, the velocity and power number changed by less than 3% in the regions of high velocity gradients.Therefore, 1 086 432 cells were employed. The same mesh density was used to determine the number of cells for the other 6PBT impellers with differently geometrical characteristics.

Fig. 2. Computational grids of the stirred system

No slip boundary conditions were imposed at the solid walls of the tank and the impeller, while the free surface at the top of the vessel was treated as a flat, shear free boundary. The xanthan gum solution rheology was modeled as Herschel-Bulkley fluid. Simulations were considered converged when the scaled residuals were below 1× 1 0−5for each transport equation. The original condition was determined as 0.

4 Results and Discussions

4.1 Validation of CFD model

CFD results for the power consumption of the 6PBT impeller (= 0.2and θ= 30◦) in glycerine solution at different rotational speeds were compared to experimental data (Fig. 3) to validate the model. These results show good agreement between calculated power consumption and the experimentally determined values,which validated the laminar flow model developed in this study.

Fig. 3. Comparison between calculated powers and experimental values at different rotational speeds

Fig. 4 shows the calculated power number Npversus the apparent Reynolds number*Re in Newtonian and pseudoplastic fluids. It can be seen that the line with the slope of −1 fits the data quite well at*Re less than 30,namely, the critical Reynolds number is 30 in laminar regime for pseudoplastic fluids. Based on the apparent viscosity method, all the power number curves for shear-thinning fluids are in coincidence with those of Newtonian fluids.

Fig. 4. Calculated power number vs. apparent Reynolds number for 6PBT impeller

4.2 CFD solution of ks and Kp

Fig. 5 shows typical power consumption of the shear thinning fluids in laminar regime for illustrating the effects of rheological index (using 6PBT impeller withand θ= 30◦). It is observed that power consumption decreases as a function of the level of rheological index for a given Rne, and a group of parallel lines are also presented with the slope of −1 from a log-log plot of Npversus Ren. Thus, Kpnvalues are dependent on n value and decrease with n.

Fig. 5. Curve of Np vs Rne for 6PBT impeller

The relationship curve of ln Kpnversus (1−n) for 6PBT impeller was plotted in Fig. 6 using the data from Newtonian and the pseudoplastic fluids based on Riger-Novak method. It can be seen that ln Kpnhas a linear relationship with (1−n). So ksis independent of the flow behavior index n for 6PBT impeller, which is consistent with the conclusion of other radial impeller, according to the above analysis. It is determined that the value of ksis 14.8 by the line slope, and the value of Kpis 84.2 as n= 1.

Fig. 6. Relationship of ln Kpn vs (1 −n)for 6PBT impeller

4.3 Complete correlations of Kp, as well as ks,with impeller geometrical characteristics

The power consumptions of ten 6PBT impellers with differently geometrical characteristics in laminar regime were numerically calculated at rotatory speed of 15 r/min,30 r/min, 45 r/min, 60 r/min, 75 r/min, and 90 r/min,respectively, by using xanthan gum solutions in water at seven mass concentrations. The Kpvalue of the 6PBT impeller could be solved by the above method, and the value of kswas obtained by the line slope of ln Kpnversus(1−n). These results are summarized in Table 2.

Table 2. Kp and ks values for 6PBT impeller with differently geometrical characteristics

For all the 6PBT impellers, a linear regression analysis on Kpand ksdata provided the following correlations in the laminar regime with a standard error of 7.31 % and 6.82%, respectively.

In order to verify the regression correlations, the power consumption of the 6PBT impellers in laminar regime was calculated again at the other rotatory speed of 9 r/min, 18 r/min, 24 r/min, 36 r/min, 54 r/min, and 72 r/min,respectively. Table 3 shows the computed results.

Table 3. Kp and ks values of the 6PBT impellers at other speeds

The following correlations were obtained by the linear regression analysis on Kpand ksdata:

The standard errors of the two correlations on Kpand ksare 8.47 % and 7.61%, respectively. It can be seen that the standard errors have very slight variations. Therefore, the above two sets of Kpandsk data (in Table 2 and Table 3)were put together and a linear regression analysis was conducted once again. Kpand kscould be correlated by the following equations with a standard error of 6.80 % and 5.93 %, respectively.

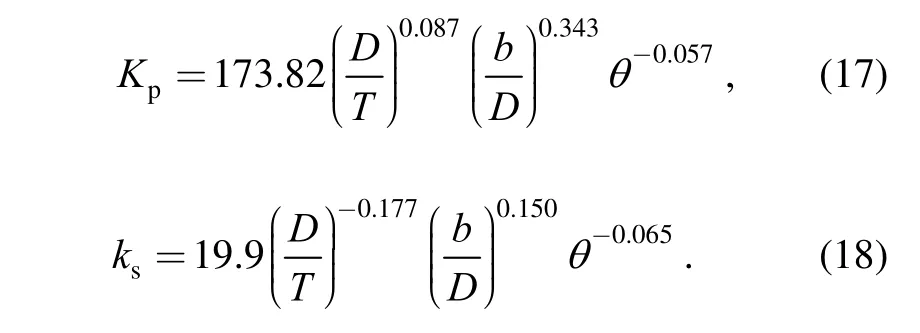
It is noticed that the values of the standard error drop slightly, which indicates that the computed value of Kpand ks, obtained by the above three sets of the complete correlations, seems similar. The error of 6.80 %and 5.93 % on Kpand ksdata, respectively, is a fully acceptable result for engineering design. Here, Eqs. (17)and (18) are adopted as the final regression correlations in this study to solve the Kpand ksvalue of the 6PBT impeller. The ranges of two correlations covered are

5 Conclusions

(1) Ten types of 6PBT impeller were investigated quantitatively in terms of power consumption as a function of impeller geometry and the pseudoplasticity of the fluid in the laminar region by using the CFD method. The numerical power consumption results with Newtonian fluid were in good agreement with the experimental data, which validated the laminar model developed in this study.

(2) A shift of the upper limit Reynolds number was observed as 30 in various shear thinning fluids for the laminar regime towards transitional flow regime.

(3) For 6PBT impeller, based on Rieger and Novak’s method, the Kpnvalue is close dependent on n value and decrease with n. The ln Kpnhas a linear relationship with(1-n), therefore, ksis nearly independent of n value even for highly shear thinning fluids and depends only on the impeller geometrical characteristics.

(4) The computed data of Kpand ksfrom the slope method are correlated with the geometrical ratiosand θ through the linear regression analysis with different speeds. The standard errors of the two correlations, Kpand ks, are 6.80 % and 5.93 %,respectively, values acceptable for engineering design. As a result, the correlations can be used to predict accurately the power consumption and average shear rate of pseudoplastic fluids in laminar flow.

[1] EIN-MOZAFFARI F, UPRETI S R. Using ultrasonic doppler velocimetry and CFD modeling to investigate the mixing of non-Newtonian fluids possessing yield stress[J]. Chem Eng Res Des,2009, 87(4): 515–523.

[2] METZNER A B, OTTO R E. Agitation of non-Newtonian fluids[J].AIChE J, 1957, 3(1): 3–11.

[3] SESTAK J, ZITNY R, HOUSKA M. Anchor-agitated systems:Power input correlation for pseudoplastic and thixotropic fluids in equilibrium[J]. AIChE J, 1986, 32(1): 155–158.

[4] TANGUY P A, LACROIX R, BERTRAND F, et al. Finite element analysis of viscous mixing with a helical ribbon-screw impeller[J].AIChE J, 1992, 38(6): 939–944.

[5] BECKNER J L, SMITH J M. Anchor-agitated systems: Power input with Newtonian and pseudo-plastic fluids[J]. Trans Instn Chem Engrs, 1966, 44(6): 224–236.

[6] SAWINSKY J, BALINT A, BENDE S. Conversion for laminar flow of bingham plastic fluids in an isothermal tube reactor[J].Chem Eng Sci, 1988, 43(5): 1209–1211.

[7] CALDERBANK P H, MOO-YANG M B. Power characteristics of agitators for mixing of Newtonian and non-Newtonian fluids[J].Trans Instn Chem Engrs, 1961, 39(5): 337–347.

[8] SCHILO D. Power requirements of tangential stirrers for stirring non-Newtonian liquids[J]. Chem Ing Tech, 1969, 41(5–6): 253–259.

[9] TANGUY P A, THIBAULT F, DE LA FUENTE E B. A new investigation of the Metzner-Otto concept for anchor mixing impellers[J]. Can J Chem Eng, 1996, 74(2): 222–228.

[10] CARREAU P J, CHHABRA R P, CHENG J. Effect of rheological properties on power consumption with helical ribbon agitators[J].AIChE J, 1993, 39(9): 1421–1430.

[11] POLLARD J, KANTYKA T A. Heat transfer to agitated non-Newtonian fluids [J]. Trans Instn Chem Engrs, 1969, 47(1):21–27.

[12] RIEGER F, NOVAK V. Power consumption scale-up in agitating non-Newtonian fluids[J]. Chem Eng Sci, 1974, 29(11): 2229–2234.

[13] BRITO-DE LA FUENTE E, CHOPLIN L, TANGUY P A. Mixing with helical ribbon impellers: effect of highly shear thinning behaviour and impeller geometry [J]. Chem Eng Res Des, 1997,75A1(A1): 45–52.

[14] LUAN Deyu, ZHOU Shenjie, CHEN Songying, et al..，Investigation on the chaotic agitation of pseudoplastic fluid with a perturbed six-bent-bladed impeller [J]. China Chem Eng, 2011, 39(9): 41–46.(in Chinese)

[15] NOVAK V, RIEGER F. Homogenization with helical screw agitator[J]. Trans Inst Chem Eng, 1969, 47 (10): 335–340.

[16] PAKZAD L, EIN-MOZAFFARI F, CHAN P. Using electrical resistance tomography and computational fluid dynamics modeling to study the formation of cavern in the mixing of pseudoplastic fluids possessing yield stress[J]. Chem Eng Sci, 2008, 63(9):2508–2522.

[17] SAEED S, EIN-MOZAFFARI F. Using dynamic tests to study the continuous mixing of xanthan gum solutions[J]. Chem Technol Biotechnol, 2008, 83(4): 559–568.

[18] AMANULLAH A, HJORTH S A, NIENOW A W. Cavern sizes generated in highly shear thinning viscous fluids by SCABA 3SHP1 impeller[J]. FoodBioprod Process, 1997, 75(4): 232–238.

[19] WANG Jiajun, FENG Lianfeng, GU Xueping, et al. Power consumption of inner-outer helical ribbon impellers in viscous Newtonian and non-Newtonian fluids[J]. Chem Eng Sci, 2000,55(12): 2339–2342.

[20] BRUCATO A, CIOFALO M, CRISFI F, et al. Numerical prediction of flow fields in baffled stirred vessels: a comparison of alternative modeling approaches[J]. Chem Eng Sci, 1998, 53(21): 3653–3684.

[21] DEEN N G, SOLBERG T, HJERTAGER B H. Flow generated by an aerated Rushton impeller: Two-phase PIV experiments and numerical simulations[J]. Can J Chem Eng, 2002, 80(4): 638–652.