An Improved Cooperative Adaptive Cruise Control (CACC) Algorithm Considering Invalid Communication
WANG Pangwei, WANG Yunpeng, YU Guizhen, and TANG Tieqiao
School of Transportation Science and Engineering, Beihang University, Beijing 100191, China
1 Introduction
Recent improvements in sensing, communication, and computing technologies have led to the development of driver-assistance systems (DAS). Adaptive cruise control(ACC) system is the first commercial implementation of DAS[1]. ACC aims to relieve drivers from manually performing a repetitive and boring task, and to automatically maintain cruise driving while assisting them in reducing crashes. Extending the standard ACC functionality with wireless inter-vehicle communication enables driving at smaller inter-vehicle distances while maintains string stability[2]. Such extended functionality is called cooperative adaptive cruise control (CACC).
A vast amount of literature on CACC is available. NAUS,et al[3], worked on CACC setup aiming at ensuring the feasibility of real-world implementation. However, in their studies, all vehicles were assumed to communicate with their preceding vehicle only. Communication among multiple vehicles or between a vehicle and a designated platoon leading vehicle was not considered. GIRARD,et al[4], from the University of California Berkeley,established a fuzzy control algorithm and a collision warning model for CACC. Meanwhile, GERRIT, et al[5],from the Eindhoven University of Technology, established a CACC model based on the variable structure sliding control algorithm and analyzed the stability with frequency response. Several other researchers used longitudinal control algorithms to design CACC controllers for vehicle platoons[6–12]and intelligent vehicle highway system(IVHS)[14–15]. ZHANG, et al[13], applied vector Lyapunov function approach to longitudinal control of vehicles in a platoon, and the controller was established by sliding mode control method.
The design of controllers for the CACC system requires the specification of string stability. A precise definition of string stability was provided by CHU[17]. String stability refers to the capability in which any perturbation of the velocity or position of the leading vehicle will not result in amplified fluctuations to the following vehicle’s velocity and position. XIAO, et al[21–25], considered the existence of delay factors in the sensors and actuators of communication systems. He analyzed the CACC string stability based on different information frameworks and then simulated the results.
A CACC algorithm considering invalid communication has not yet been developed according to the literature review. This is the reason why this paper focuses on designing an improved algorithm that ensures the functionality of the CACC system even if inter-vehicle communication is partially invalid. The improved algorithm is based on the sliding mode control algorithm and can adjust the CACC structure to ensure string stability.Therefore, the algorithm can prevent vehicle chain collisions even with communication system partially invalid. The feasibility of the algorithm has been verified based on MATLAB/Simulink.
The organization of this paper is described as follows.Section 2 focuses on designing the CACC hierarchical controller based on sliding control and obtains the string stable conditions. Section 3 improves the CACC hierarchical controller under the circumstance of communication being partially invalid and obtains the relevant string stability conditions. Section 4 then presents the simulation results of the MATLAB/Simulink model.Finally, section 5 summarizes the conclusions and proposes directions for further research.
2 CACC Controller
As in many other longitudinal vehicle control applications, the CACC hierarchical controller in this paper also consists of an upper control layer and a lower execution layer, as shown in Fig. 1. The upper control layer calculates the value of the desired acceleration using all the relevant information obtained by the CACC module, and then transfers the information to the lower execution layer.The lower execution layer achieves the desired acceleration by the actuators, which are controlled by the relevant control module. This process is the core of the CACC controller.
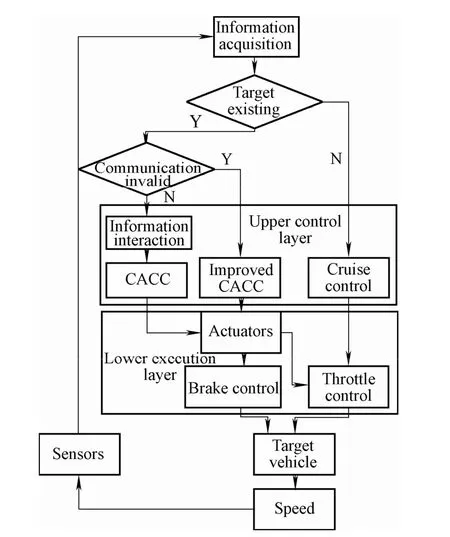
Fig. 1. Structure of CACC
2.1 CACC algorithm based on sliding control
In the CACC platoon, vehicles communicate with each other to exchange information, thus facilitating fleet cooperative control. The latest Wi-Fi is based on the IEEE802.11g communication protocol and utilizes 2.4 GHz band, transmission speed of up to 54 Mb/s, and maximum transmission distance of 6.5 km. Such communication technology is suitable for vehicle communications owing to its high stability.
The leading vehicle of the platoon controlled by the CACC controller runs along certain orbits, followed by the other vehicles. The platoon structure is shown in Fig. 2.

Fig. 2. CACC platoon
In Fig. 2, the CACC platoon obtains the acceleration information by the communication system according to the CACC algorithm with Wi-Fi. Hence, the CACC controller Y can sum the spacing error and calculate the relative speed of the following vehicles, which tends to approach zero:
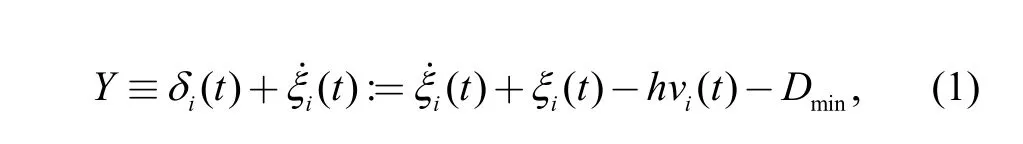
All the above can be represented as follows:
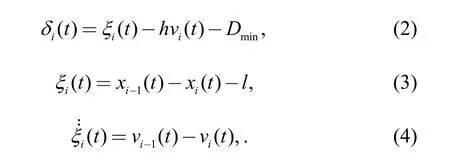
where l is the vehicle length. Using the sliding control method, we can obtainwhenthe equation is true, andis the control parameter.
Taking the time delay of the actuators and sensors into consideration, the CACC controller Ui(t )is represented as follows:
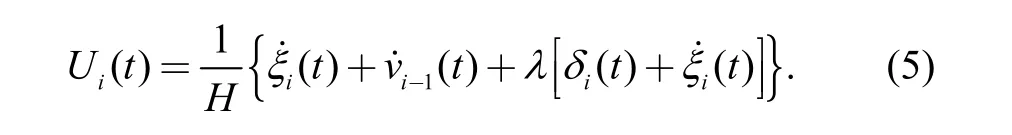
Delay time exists in the data transmission process in actual communication systems; hence it must be taken into account when calculating the expected acceleration algorithm. The time compensation is represented by Δ,which means that the expression of the control law Ui(t )is replaced with:

2.2 String stability of the CACC platoon
According to Ref. [21], based on the vehicle longitudinal dynamics model, vehicle i has a delay of Δ seconds to respond to the actuators, and suffers a lag of τ seconds to respond to the commanding signal. Combining the equations of the controller, the longitudinal dynamics equation of the following vehicle i is as follows:
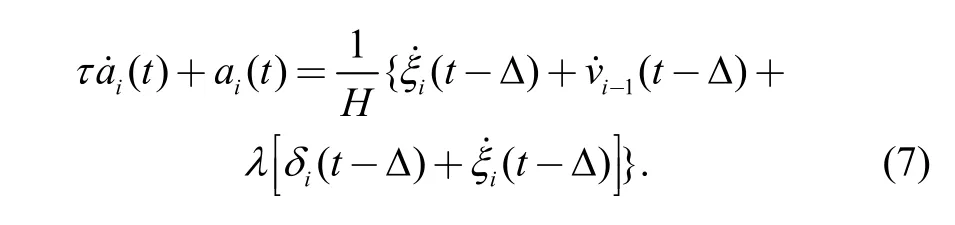
Similarly, the longitudinal dynamics equation of the following vehicle i−1 is as the following:
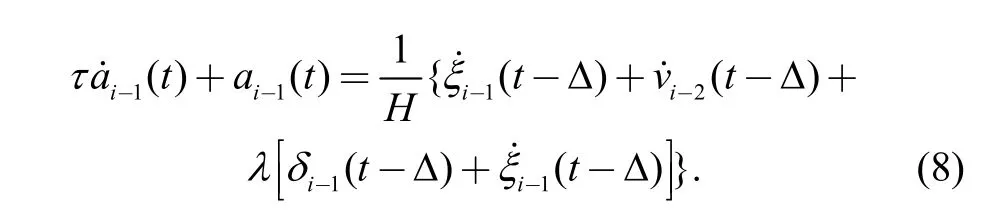
The above two equations show the acceleration and spacing error, and the distance between vehicle i and vehicle i−1. After subtracting Eq. (8) from Eq. (7), the following Eq. (9) is obtained through a differential and a Laplace transform:
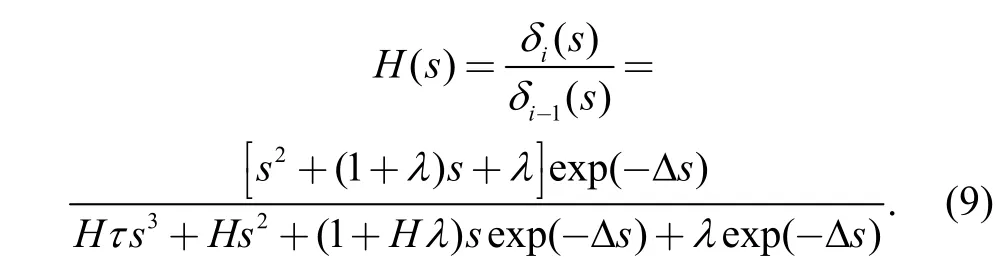
Eq. (9) is the spacing error dynamic model for a platoon controlled by CACC in the frequency domain. In order to maintain stability, which means keepingthe following two conditions should be satisfied.
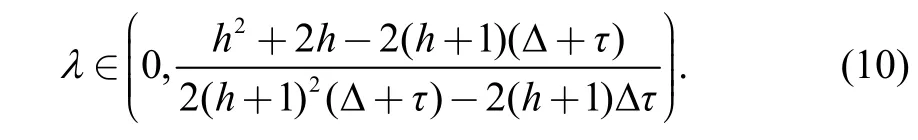
Condition 2: Because the controller parameter>0 ,fixed time spacing should be described as follows:where Δ is the delay time of communication and τ is the delay time of the actuators.

When the two conditions are satisfied,can be founded for anyand the platoon controlled by CACC can maintain string stability.
3 Improved CACC Algorithm in Case of Communication Being Partially Invalid
In this section, we demonstrate that the traditional CACC algorithm cannot ensure string stability under consideration of the communication being partially invalid, and the CACC algorithm how to be improved to meet the requirements of string stability.
3.1 Improved control algorithm for vehicle i
In case of invalid communication for vehicle i, the following vehicle i cannot obtain the acceleration information of the preceding vehicle i−1, making the traditional CACC algorithm dysfunctional. Therefore, the algorithm should be improved in cases such that the communication between vehicle i and vehicle i-1 is not available, but vehicle i−1 can communicate with vehicle i+1, as shown in Fig. 3.

Fig. 3. CACC platoon in cases of invalid communication(vehicle i cannot communicate with vehicle i-1)
In Fig. 3, according to string stability, the communication of vehicle i is invalid, making it unable to obtain the acceleration information of the preceding vehicle.
The aim of the controller design is to make the spacing error at a minimum, hence it is important to maintain the ideal distance. The equation is as follows:

Using the sliding control method, we can obtainwhenthe equation is true, andiis the control parameter.
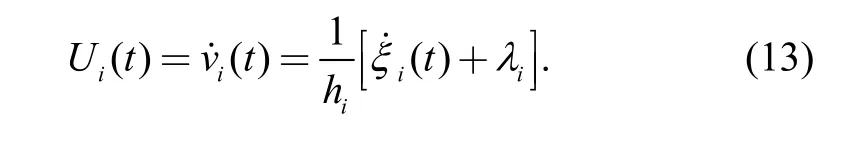
Taking the time delays of the actuators and sensors into consideration, when the communication of vehicle i is invalid, the CACC controller Ui(t )is as follows:
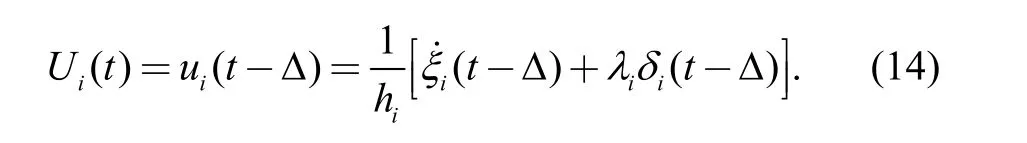
Based on the vehicle longitudinal dynamics model, the following equation is obtained:
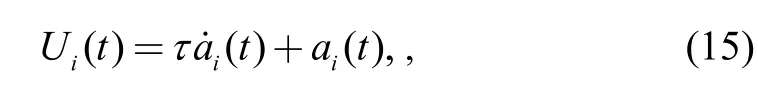
where ai(t) is the acceleration of the vehicle i; The lag time of the actuators is denoted by(s) . Combining this with the equation of the controller, the longitudinal dynamics equations of the following vehicle i and its preceding vehicle i−1 are shown as follows:
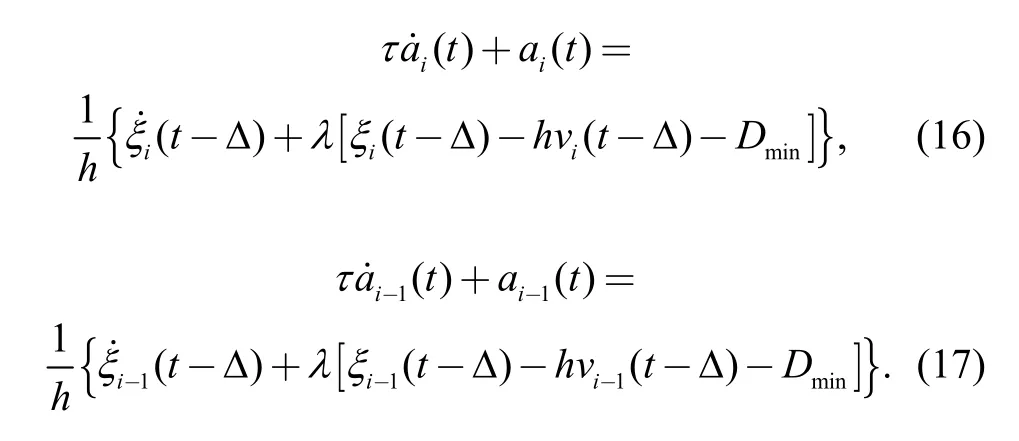
After subtracting Eq. (17) from Eq. (16) to obtain a differential and a Laplace transform, the following is concluded:
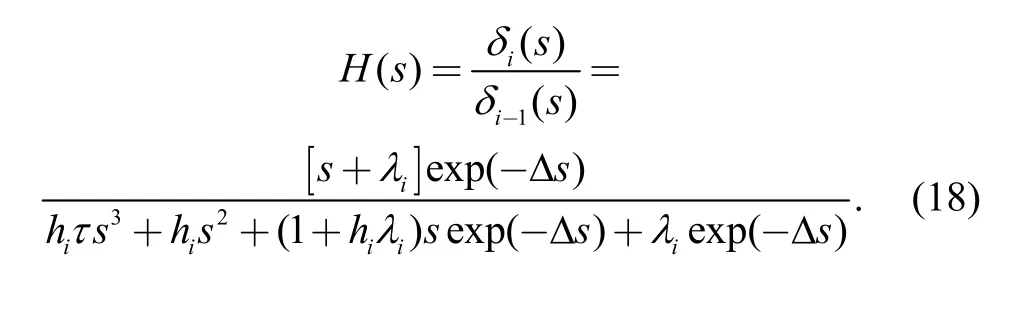
To maintain communication stability, when the communication of vehicle i is invalid,must be satisfied; hence the range of the controller parameteris as follows:
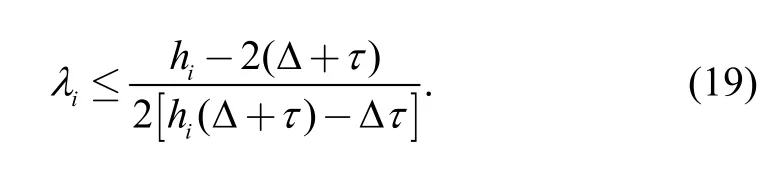
In addition, because the controller parameter meets> 0, the fixed time spacing should be satisfied as follows:

3.2 Improved control algorithm for vehicle i+1
In case of invalid communication for vehicle i, the following vehicle i+1 cannot obtain the acceleration information of the preceding vehicle i. Vehicle i+1 will communicate with vehicle i−1, and vehicle i+1 will obtain the acceleration information of vehicle i−1. The controlleris shown as follows:
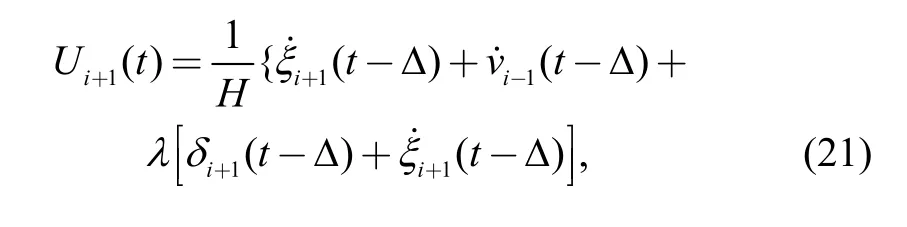
then,
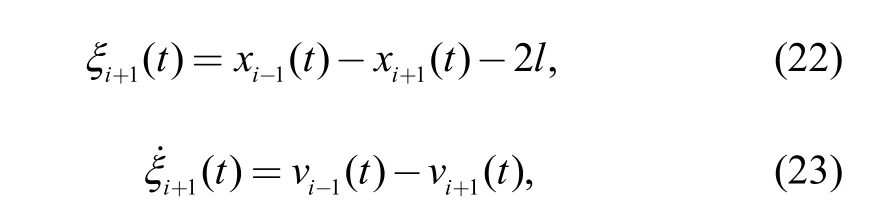
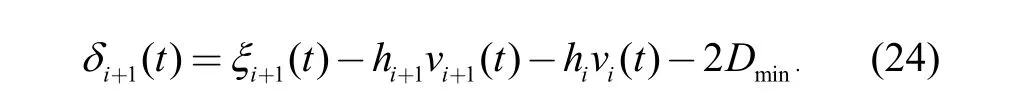
Based on the vehicle longitudinal dynamics model,the lag time of the actuators is denoted by τ(s). Combining this with the equation of the controller, the longitudinal dynamics equations of the following vehicle i+1 and its preceding vehicle i−1 are shown as follows:
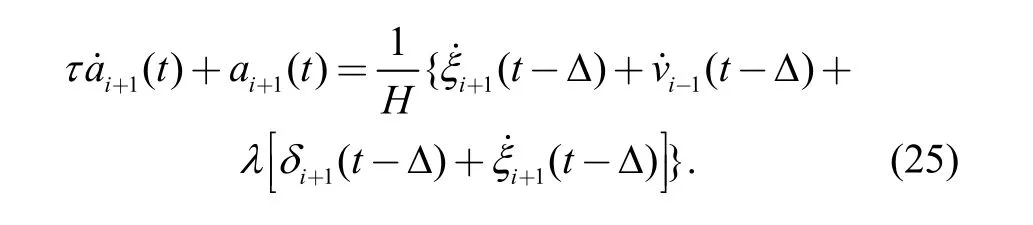
Similarly, the longitudinal dynamics equation of the following vehicle i−1 is shown as below:
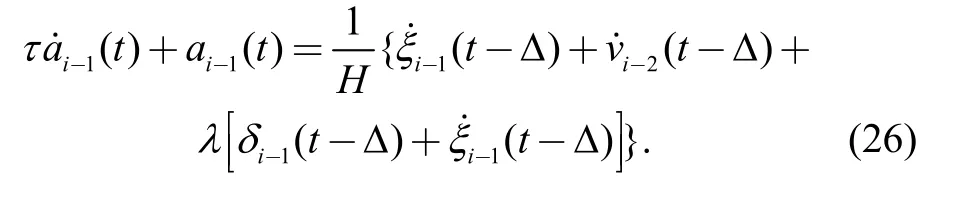
After subtracting Eq. (26) from Eq. (25) to obtain a differential and a Laplace transform, the following equation is obtained:

To maintain communication stability when communication of the vehicle i is invalid,must be satisfied; hence the range of controller parameteris as follows:> 0, the fixed time spacing should be satisfied as
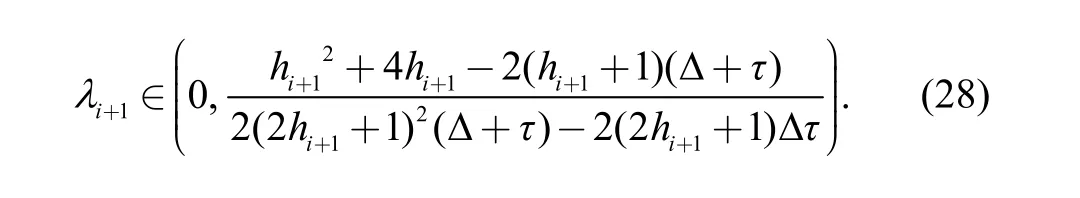
Additionally, because the controller parameter meets
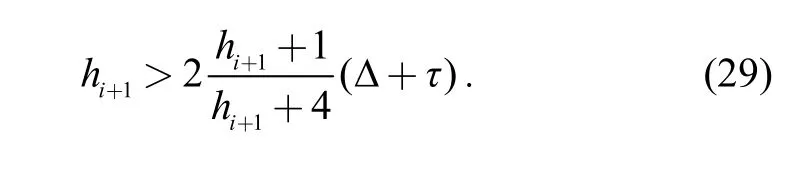
The controller parameters should be adjusted as above to ensure communication stability and keep the vehicle i in the platoon.
In conclusion, the sliding controller parameters should be satisfied as follows:
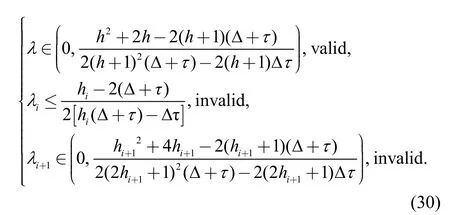
The fixed time spacing should be satisfied as follows:
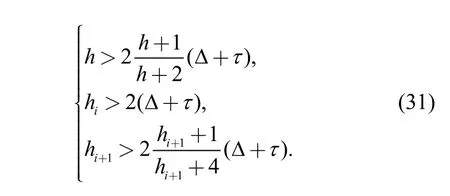
In case of invalid communication for vehicle i, the traditional CACC algorithm should be adjusted, and the algorithm for vehicle i and vehicle i+1 should be improved with the other maintaining invariants. The controller parameters should be adjusted to maintain communication stability when the communication of vehicle i is invalid and ensure that vehicle i is kept in the platoon. Chain collisions arising from invalid communication can be avoided.
4 Simulation Results
In the initial situation, the leading vehicle stands still, v0=0 m/s and a0=0 m/s2. After continuous acceleration, the speed of the leading vehicle reaches vf=40 m/s at time t=20 s.Its speed then remains constant. The other four vehicles’initial state is the same as that of the head vehicle, and they are as following.The initial spacing between any two vehicles is 5 m. The parameters of CACC are shown in Table 1.

Table 1. Parameters of the traditional CACC
4.1 Results of traditional CACC in case of communication being partially invalid
In this case, we assume that the communication of the third vehicle is invalid at t=10 s. The result of the traditional CACC platoon is shown as Figs. 4–6.
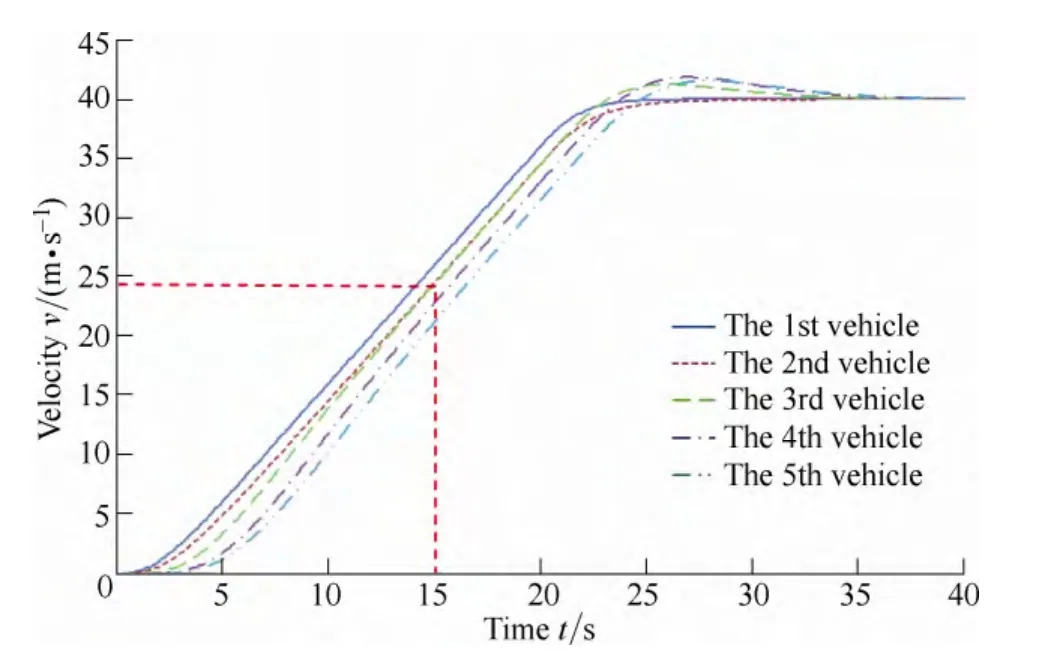
Fig. 4. Velocity curve of the traditional CACC platoon
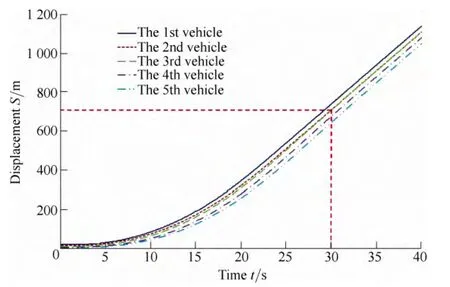
Fig. 5. Displacement curve of the traditional CACC platoon
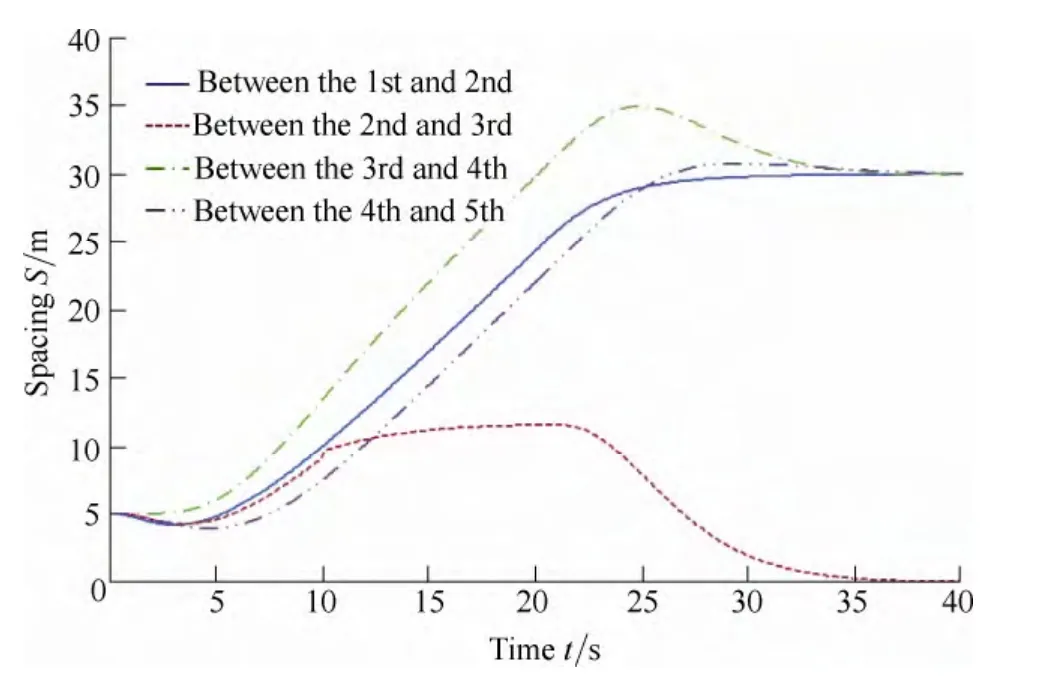
Fig. 6. Spacing curve of the traditional CACC platoon
As shown in the above figures, at t=15 s, the speed of the third vehicle is higher than that of the second vehicle;and the conditions of string stability are not satisfied. At t=30 s, the displacement of the third vehicle is more than that of the second vehicle, and the collision accident occurred. In addition, the spacing between the second and third vehicles tends to reach zero. String stability cannot be maintained, and chain collisions happen under actual circumstances.
4.2 Results of the improved CACC in case of communication being partially invalid
In order to solve the problem of the communication of the third vehicle being invalid, the CACC controller of the third vehicle is improved, and the parameters are adjusted according to Eq. (30) and Eq. (31) to meet the requirements of string stability as shown in Table 2.

Table 2. Adjusted parameters of CACC
The simulation result of the improved CACC platoon is shown as Figs. 7–9. As shown in Figs. 7–9, the third vehicle’s communication turns invalid at t=10 s, and the control algorithm switches at the same time to the improved CACC. As a result, the spacing between the third vehicle and the second vehicle was enlarged to prevent accidents. The displacement of the third vehicle is always less than that of the second vehicle, and there is no impact to the other vehicles’ spacing. Chain collisions are therefore prevented.
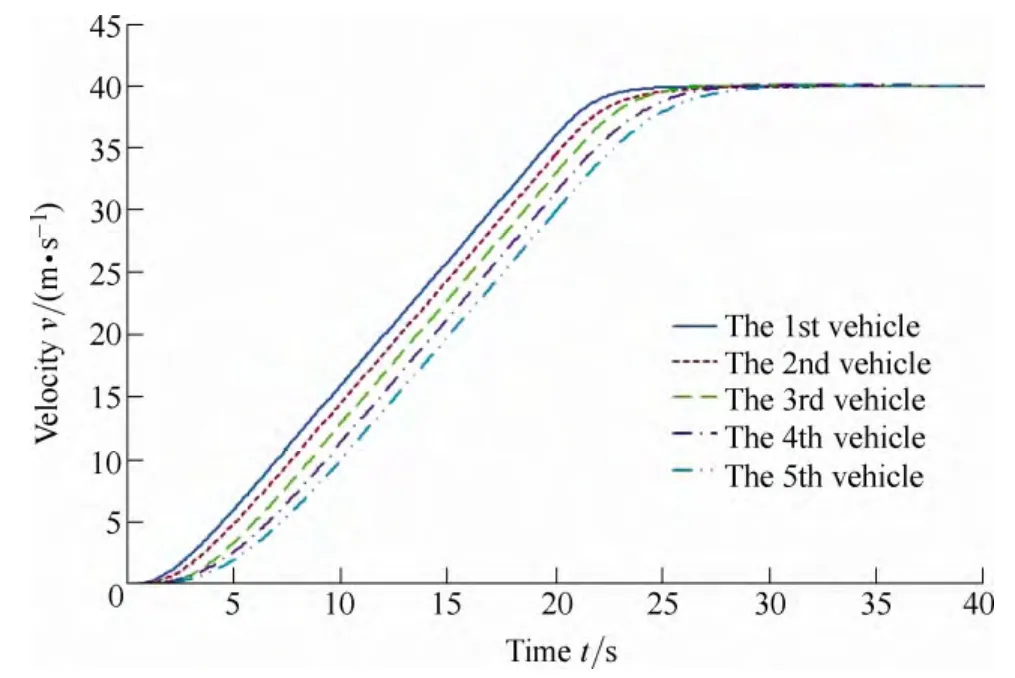
Fig. 7. Velocity curve of the improved CACC platoon
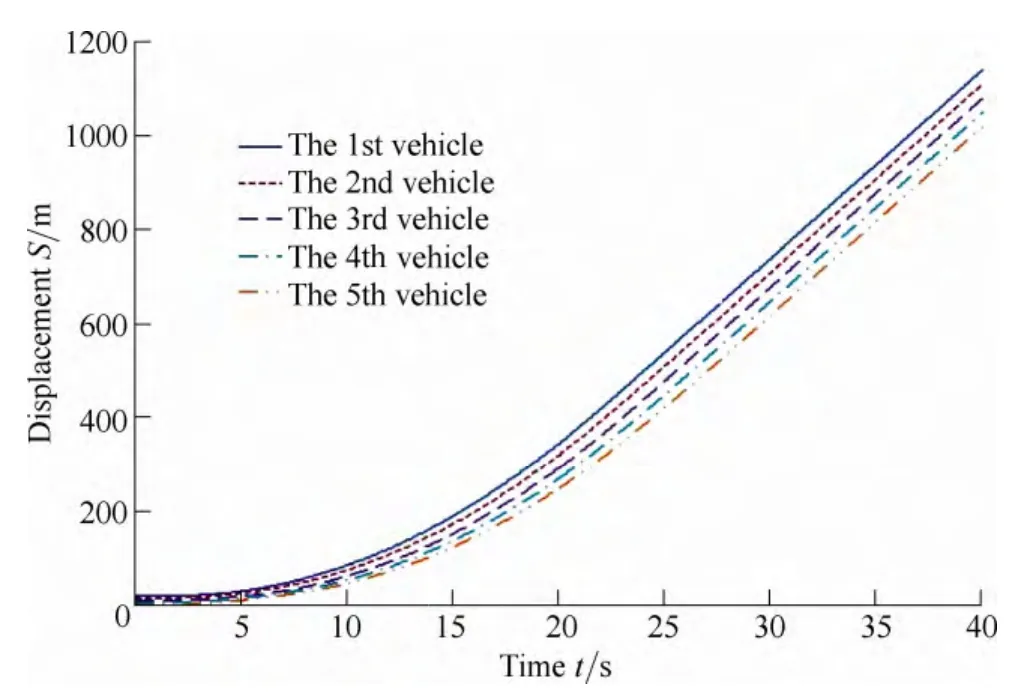
Fig. 8. Displacement curve of the improved CACC platoon
5 Conclusions
(1) This paper presents the improved CACC algorithm based on the sliding mode control algorithm. It establishes a dynamic model of vehicle spacing deviation in a platoon and analyzes the vehicle stability conditions under improved CACC.

Fig. 9. Spacing curve of the improved CACC platoon
(2) The CACC algorithm is verified through an automatic platoon model involving five vehicles.
(3) The paper analyzes the improved CACC algorithm and the adjusted controller parameters to maintain string stability under the condition of communication being partially invalid.
(4) The feasibility of the algorithm has been demonstrated through model simulation. The improved CACC algorithm achieves vehicle-following effects and effectively maintains string stability.
(5) It covers the shortages of the traditional CACC algorithm by avoiding oscillation of vehicle spacing and chain collision accidents caused by partially invalid communication.
[1] VANDER WERF J, SHLADOVER S E, MILLER M A, et al.Effects of adaptive cruise control systems on highway traffic flow capacity[J]. Transportation Research Record: Journal of the Transportation Research Board, 2002, 1800(1): 78–84.
[2] RAJAMANI R, ZHU C. Semi-autonomous adaptive cruise control systems[J]. Vehicular Technology, IEEE Transactions on, 2002,51(5): 1186–1192.
[3] NAUS G, VUGTS R, PLOEG J, et al. Towards on-the-road implementation of cooperative adaptive cruise control[C]//Proceedings of the 16th World Congress and Publication exhibition on Intelligent Transport Systems and Services, Stockholm Sweden,2009: 21–25.
[4] GIRARD A R, SOUSA J B, MISENER J A, et al. A control architecture for integrated cooperative cruise control and collision warning systems[C]//The 40th IEEE Conference on Decision and Control, Orlando, 2001, 2: 1491–1496.
[5] GERRIT J, RENÉ P, JEROEN P, et al. String-stable CACC design and experimental validation: A frequency-domain approach[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4268–4278.
[6] SHLADOVER S E. Longitudinal control of automated guide way transit vehicles within platoons[J]. Journal of Dynamic Systems,Measurement and Control, 1978, 100(4): 302–310.
[7] ZHANG Jian, IOANNOU P A. Longitudinal control of heavy trucks in mixed traffic: Environmental and fuel economy considerations[J].Intelligent Transportation Systems, IEEE Transactions on, 2006,7(l): 92–104.
[8] SHEIKHOLESLAM S, DESOER C A. Control of interconnected nonlinear dynamical systems: The platoon problem[J]. Automatic Control, IEEE Transactions on, 1992, 37(6): 806–810.
[9] DRUZHININA M, MOKLEGAARD L, STEFANOPOULOU A.Parameter estimation and supervisory techniques for robust longitudinal control of heavy vehicles[R]. PATH Research Report,UCB-ITS-PRR-2003-15, University of California, Berkeley, USA, 2003.
[10] FUJIOKA T, ASO M, KIMURA T. Longitudinal vehicle following control for autonomous driving[C]//Proceedings of International Symposium on Advanced Vehicle Control, Aachen, Germany, 1996:1293–1304.
[11] SWAROOP D, HEDRICK J K, CHOI S B. Direct adaptive longitudinal control of vehicle platoons[J]. IEEE Transactions on Vehicular Technology, 2001, 50(1): 150–161.
[12] SAINTE-MARIE J, MAMMAR S, NOUVELIERE L, et al.Sub-optimal longitudinal control of road vehicles with capacity and safety considerations[J]. ASME Journal of Dynamic Systems,Measurement, and Control, 2004, 126(l): 26–35.
[13] ZHANG J, SUDA Y, IWASA T, et al. Vector Lyapunov function approach to longitudinal control of vehicles in a platoon[J]. JSME International Journal (Series C), 2004, 47(2): 653–658.
[14] HEDRIEK K, MCMAHON D, NARENDRAN V, et al.Longitudinal vehicle controller design for IVHS systems[C]//Proceedings of the American Control Conference,Boston, 1991: 3107–3111.
[15] MCMAHON D. Longitudinal vehicle controller design for IVHS:Theory and experiment[C]//Proceedings of the American Control Conference, Chicago, 1992: 1753–1757.
[16] NOUVELIEREA L, MAMMAR S. Experimental vehicle longitudinal control using a second order sliding model technique[J].Control Engineering Practice, 2007, 15(8): 943–954.
[17] CHU K. Decentralized control of high-speed vehicular strings[J].Transportation Science, 1974, 8(3): 361–384.
[18] YI K, HONG J, KWON Y D. A vehicle control algorithm for stop-and-go cruise control[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2001, 215(10): 1099–1115.
[19] LUO Yugong, CHEN Tao, ZHOU Lei, et al. Adaptive cruise control system of besturn intelligent hybrid electric vehicle[J]. Chinese Journal of Mechanical Engineering, 2010, 46(6): 2–7. (in Chinese)
[20] JOSE E, NARANJO. Adaptive fuzzy control for inter-vehicle gap keeping[J]. IEEE Transactions on Intelligent Transportations, 2003,4(3): 132–142.
[21] XIAO Lingyun, GAO Feng. On string stable control of platoon of automated vehicles with predecessor-successor information framework[J]. Chinese Journal of Mechanical Engineering, 2010,23(5): 627–634.
[22] XIAO Lingyun, GAO Feng. Practical string stability of platoon of adaptive cruise control vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1184–1194.
[23] XIAO Lingyun, GAO Feng. A comprehensive review of the development of adaptive cruise control (ACC) systems[J]. Vehicle System Dynamics, 2010, 48(10): 1167–1192.
[24] XIAO Lingyun, GAO Feng. Effect of information delay on string stability of platoon of automated vehicles under typical information frameworks[J]. Journal of Central South University of Technology,2010, 17(6): 1271–1278.
[25] XIAO Lingyun, DARBHA S, GAO Feng. Stability of string of adaptive cruise control vehicles with parasitic delays and lags[C]//Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 2008:1101–1106.
[26] PEPPARD L. String stability of relative-motion PID vehicle control systems[J]. IEEE Transactions on Automatic Control, 1974, 19(5):579–581.
[27] PEI Xiaofei, LIU Zhaodu, MA Guocheng, et al. Multi-mode switching controller for vehicle adaptive cruise control system[J].Chinese Journal of Mechanical Engineering, 2012, 48(10): 96–102.
 Chinese Journal of Mechanical Engineering2014年3期
Chinese Journal of Mechanical Engineering2014年3期
- Chinese Journal of Mechanical Engineering的其它文章
- Theoretical Analysis and Experimental Verification on Valve-less Piezoelectric Pump with Hemisphere-segment Bluff-body
- Carbody Structural Lightweighting Based on Implicit Parameterized Model
- Prediction-based Manufacturing Center Self-adaptive Demand Side Energy Optimization in Cyber Physical Systems
- Effectiveness of a Passive-active Vibration Isolation System with Actuator Constraints
- Numerical Simulation and Analysis of Power Consumption and Metzner-Otto Constant for Impeller of 6PBT
- Proceeding of Human Exoskeleton Technology and Discussions on Future Research
