水下蒸汽涡轮发动机变工况热力特性数值分析研究

张方方，张振山，梁伟阁，王郑力

(海军工程大学 兵器工程系，湖北 武汉430033)

0 引言

涡轮机具有比功率大、比耗量小、输出转速高、运行平稳、机械振动和噪声小等优点，其广泛应用于航空动力［1］、舰船推进［2］以及水下航行器推进［3］等方面。在对水下航行器航速、安静性要求日益增高的今日，水下涡轮发动机势必取代活塞机成为研究热点。然而，水下涡轮机受航行器空间尺寸小、排气背压大等不利因素影响，其结构及其研究成果有别于航空动力涡轮机和舰船推进涡轮机。

文献［4］利用渐近分析方法得到了涡轮机动叶片的非线性数学模型，该模型包括三维叶轮线弹性模型、二维叶片非线性扁壳体模型以及二者的链接模型，其为动叶片气动优化设计提供基础模型;文献［5］明确了水下涡轮机数字仿真的一般步骤，为水下涡轮机数值分析提供研究思路;文献［6］给出了喷嘴出口速度的计算方法，为水下涡轮机变工况特性分析奠定基础;文献［7 -8］建立了用于深水发射装置、以常温压缩空气为工质的涡轮机带负载短时间启动过程数学模型，其为文中模型的建立提供参考;文献［9］提出了计算流体力学(CFD)技术用于水下燃气涡轮机设计的一般步骤，并将其用于涡轮机通流部分流场性能的预测，取得和实验数据吻合较好的仿真结果。上述文献研究的水下涡轮机均以空气、燃气为工质，数值分析时无需考虑工质膨胀过程中相态变化问题，也即无需考虑工质由气相转变为液相的问题。而当蒸汽涡轮机以超高膨胀比为设计工况时，若仍采用绝热膨胀理论计算喷嘴，将出现喷嘴后工质为液态水滴的情况，这显然与实际情况不符。

为此，本文将在考虑过热蒸汽绝热指数随温度变化以及喷嘴内气流摩擦、涡旋对蒸汽加热作用的基础上，建立超高膨胀比水下汽轮机的变工况计算模型。并结合案例对变压力比和喷嘴入口工质温度变化时的汽轮机热力过程开展仿真研究，验证模型的正确性。

1 数学模型

本文研究的涡轮机为部分进气、冲动式、轴流式涡轮机，其通流部分结构简图如图1所示。

由图1可知，水下蒸汽涡轮发动机变工况计算包含喷嘴计算和动叶栅计算，且涡轮级变工况能量损失不容忽视，故数学模型将从此3 个方面重点探讨水下涡轮机的变工况数值计算。图中各参数的物理意义可参考文献［10］.

图1 涡轮机通流部分示意图Fig.1 Schematic diagram of turbine flow passage component

1.1 喷嘴的变工况计算

工质的平均定压比热容cpT和绝热指数k 可由下式求解:

式中:cpT表示T 温度下过热蒸汽的平均定压比热容;Rg为水蒸汽的气体常数。

利用喷嘴设计工况速度因数φ0考虑绝热膨胀中气流摩擦和涡旋损失对工质速度的影响，根据能量守恒定律可得喷嘴喉部工质各临界参数的实际值:

式中:pc、pcr、ccr、Tcr、ρcr分别为喷嘴入口工质压力、喷嘴喉部工质临界压力、流速、温度和密度;Tc为涡轮机喷嘴入口温度。

由喷嘴喉部工质的实际临界流速ccr以及临界密度ρcr，可得涡轮机工质的实际秒耗量:

式中:nn为工作喷嘴数;为喷嘴的流量因数;At为喷嘴喉部截面积。

令涡轮机工作背压为p1，则压力比B =p1/pc，此时喷嘴出口工质理想速度c1t可得

设计工况下B、c1t分别对应设计压力比Bs和c1st. 由于设计工况下一般不利用缩放喷嘴的斜切口使气体补充膨胀加速，故此时的气流偏转角δ =0°，喷嘴速度因数φ=φ0.

当实际压力比B ＜Bs时，超音速蒸汽将在喷嘴出口处发生膨胀波。根据膨胀波形成机理和能量守恒定律计算膨胀波前、后工质的速度ce、ca及温度Te、Ta，进而计算其前、后工质马赫数Mae和Maa:

根据普朗特-迈耶函数得气流偏转角δ［11］:

此时，可得膨胀波作用下的喷嘴速度因数φ =φ0cosδ.

当实际压力比B ＞Bs时，喷嘴出口界面处将产生激波。根据绝热膨胀理论和能量守恒定律计算激波前工质速度ce=φ0c1st、温度Te=(cpTcTc-0.5c2e)/cpTe、马赫数由Mae和压力比B、Bs，根据气体动力学理论可得激波角β 的计算方法:

由激波角β 可求得斜激波切向速度分量Cτ和气流偏转角δ:

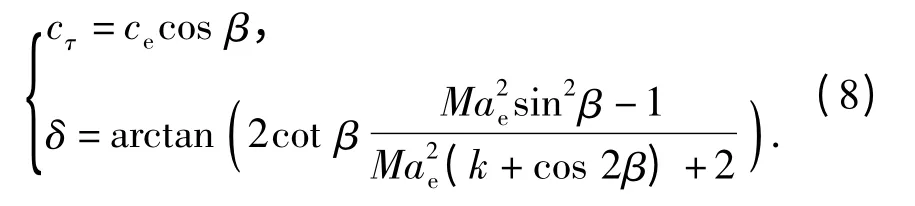
气流通过斜激波时，切向速度分量不发生变化，即cτ=ceτ=c1τ，此时根据斜激波前后气流的几何关系可得法向速度分量c1n=c1τtan(β -δ). 则激波作用下的喷嘴速度因数φ 可得

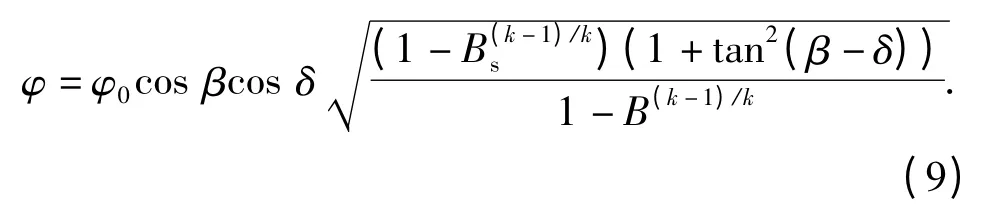
综合以上分析，变工况下喷嘴出口工质的实际速度c1=φclt及其偏转角δ 可得。

1.2 动叶栅的变工况计算

文献［12］通过引入传质负荷参数考虑压力对蒸汽机工质传递的影响，进而建立了汽轮机热力循环数学模型。本文将以此为基础，利用涡轮进出口速度三角形推导气动压力、摩擦力切向分量产生的轮周功。涡轮进出口速度三角形如图2所示。

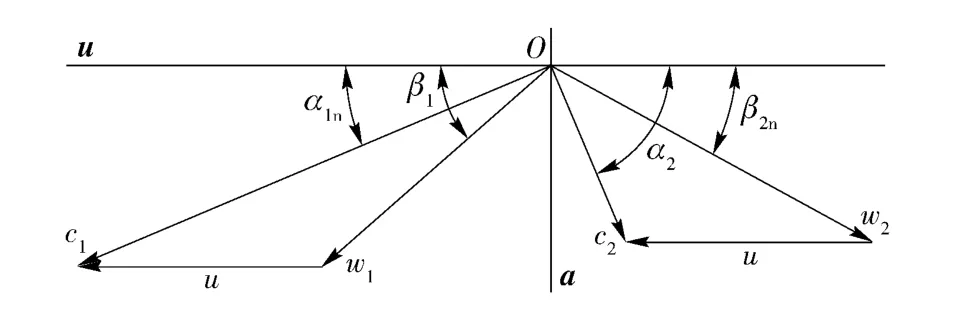
图2 涡轮进出口速度三角形Fig.2 Speed triangle of turbine at inlet and outlet

图2中，速度在u、a 方向上的投影分别对应速度的切向分量和轴向分量，其中切向分量输出轮周功。图中，u 为汽轮机的轮周线速度

式中:b 为汽轮机减速器的减速比;n、ω 分别为推进器的转速和角速度;dm为动叶栅平均直径。

涡轮机设计定型后喷嘴进气倾斜角α1n确定，则涡轮的进口速度三角形可解

式中:w1为变工况下气体流入动叶栅的相对速度，其与工作轮回转平面的夹角为β1.

对于冲动式涡轮，气体流出动叶栅的相对速度w2与w1之间存在如下关系［13］:

式中:Maw2t为工作叶片出口工质的理想马赫数，其中w2t=w1;w 为动叶栅宽度;l 为叶片高度;β1n为叶片几何流入角;ii=(β1n-β1)/β1n，为相对气流撞击角;ψ 为动叶栅速度因数，并规定当ii＞1 或ii＜-2.582时ψ =0;aψ为计算系数，并规定ii＞0 时aψ=1，ii＜0 时aψ=0.15.

涡轮机设计定型后叶片几何流出角β2n为已知量，则涡轮的出口速度三角形可解

式中:c2为气体流出动叶栅的绝对速度，其与工作轮回转平面的夹角为α2.

涡轮进出口速度三角形求解完毕后，对单个工作叶片控制体内的气流列动量定理方程，可求得工质对动叶栅的作用力Fu，进而求得涡轮级的轮周功Wu和轮周效率ηu

至此，变工况下涡轮机动叶栅的计算模型建立完毕。

1.3 变工况涡轮级能量损失计算

涡轮机运行过程中，喷嘴损失Δhn、动叶损失Δhb、余速损失Δhe、轮盘摩擦损失Δhfr以及叶高损失Δhl可由喷嘴、动叶栅的建模过程得到

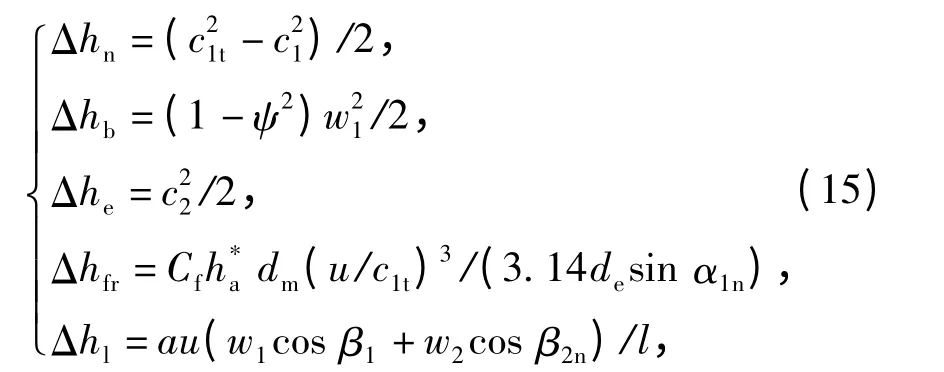
式中:Cf= 0.14(1 + 2.5w/dm)［S/(dm- l)0.1］/Re0.21，为轮盘摩擦系数［14］，其中，S 为轮盘与壳体间的间隙，Re 为燃气雷诺数;de为喷嘴有效出口直径;a 为实验系数，当叶高损失包含扇形损失时，a =1.6.

当涡轮级部分进气度ε 小于1 时存在鼓风损失Δhw和斥气损失Δhs，其可按以下经验公式计算［15］:

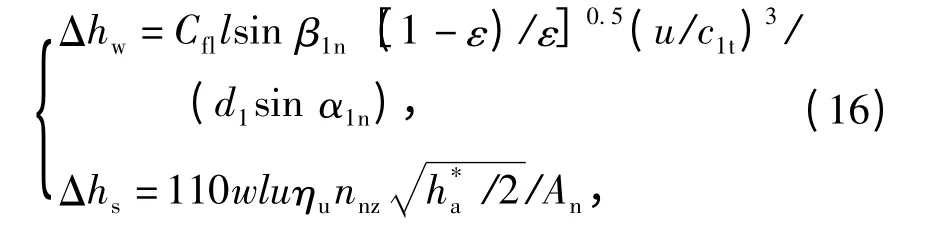
式中:Cfl为叶片处的摩擦系数;β1n为叶片几何流入角;d1为喷嘴扩张结束截面对应的直径;w 为动叶栅宽度;ηu为轮周效率;nnz为喷嘴组数;ε 和喷嘴出口椭圆面积An可由图1中的几何关系求得

式中:γ 为喷嘴的扩张角。

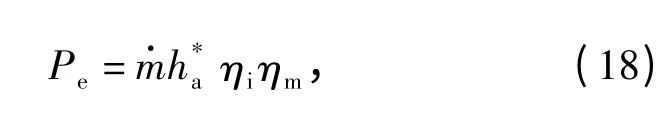
式中:ηm为整机机械系统的机械效率。

2 案例仿真及分析

由建立的数学模型编写计算程序，对某水下涡轮发动机变工况热力特性进行仿真。仿真输入参数有燃烧室出口压力pc、温度Tc以及喷嘴设计工况速度因数φ0，并结合涡轮机喷嘴、动叶栅的详尽结构参数进行仿真，可得汽轮机变工况热力过程各参数的变化规律。

2.1 变压力比时的涡轮机热力计算

2.1.1 喷嘴的计算结果及分析

利用喷嘴变工况计算模型对涡轮机喷嘴内的热功转换规律进行仿真，计算结果如图3所示。

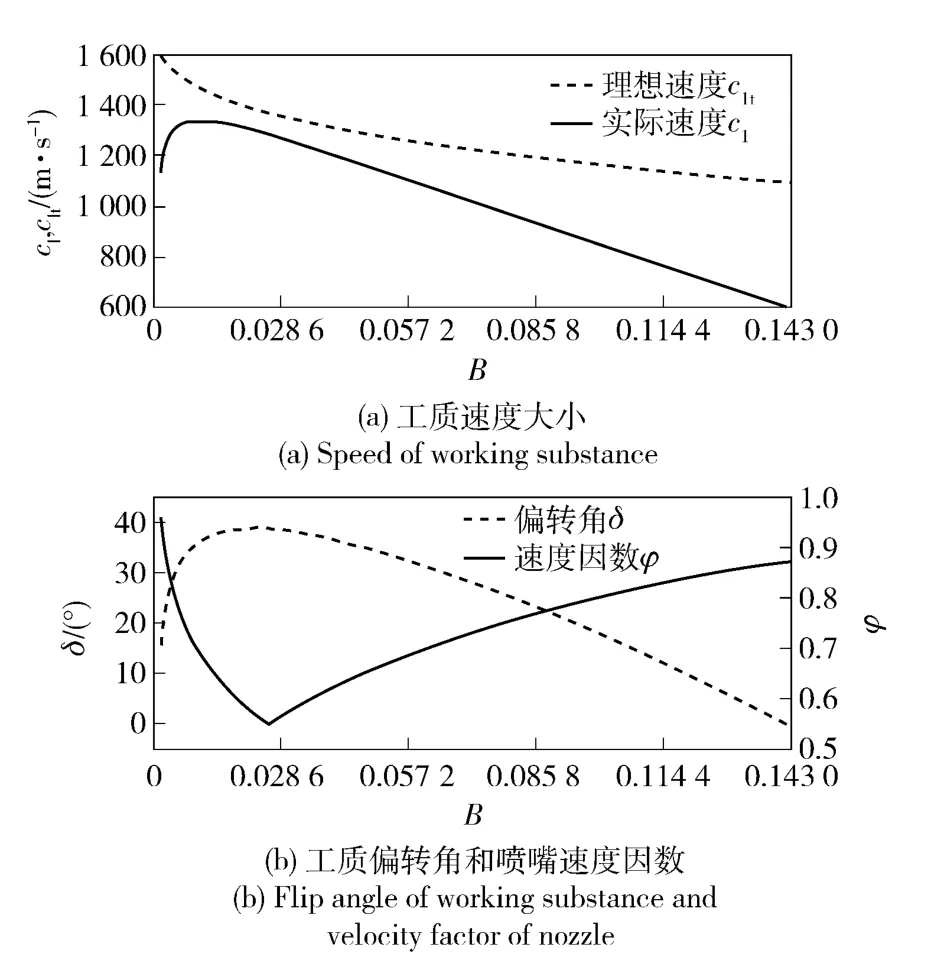
图3 变压力比下涡轮机喷嘴出口工质参数变化规律Fig.3 Variation of nozzle exit working substance parameters for turbine engine under changing pressure ratio

图3(a)、图3(b)分别给出了喷嘴出口工质理想速度c1t和实际速度c1、工质偏转角δ 和喷嘴速度因数φ 随涡轮机实际压力比的变化规律。由图3(a)可知，理想速度c1t随着实际压力比的升高逐渐减小，该变化趋势符合(4)式蕴含的规律。由图3(b)可知，随着压力比的增加，偏转角δ 呈现先减小而后增大的规律，并在设计压力比Bs处取得最小值δ=0°，这是由于设计工况下喷嘴出口处既不发生膨胀波也不产生激波;当实际压力比B ＞Bs时，喷嘴出口存在激波，且随着压力比B 的增加斜激波逐步向正激波转变，工质偏转角δ 将逐步增大;当B ＜Bs时，喷嘴出口存在膨胀波，且随着压力比B 的减小膨胀波效应越明显，工质偏转角越大。喷嘴速度因数φ 在设计压力比下取得最大值φ0，且随着偏转角δ 的增加而减小，符合图2(b)中所示的变化规律。由c1=c1tφ 可知，设计工况下c1=c1tφ0;当B ＞Bs时，c1t、φ 均随着压力比B 的增加而减小致使实际速度c1不断减小;当B ＜Bs时，c1t、φ 的变化先后起主导作用致使实际速度随着的减小呈现先增大而后减小的趋势。

由涡轮机喷嘴的仿真结果及分析可知，喷嘴出口工质各参数的变化规律反映了变工况下涡轮机喷嘴的工作特性，进而验证了变工况下喷嘴计算模型建立与仿真的正确性。

2.1.2 动叶栅的计算结果及分析

利用动叶栅变工况计算模型对汽轮机动叶栅内的热功转换规律进行仿真，结果如图4所示。

图4 变压力比下涡轮机动叶栅计算结果Fig.4 Calculated results of turbine cascade under changing pressure ratio

图4(a)给出了气流撞击角i 和动叶栅速度因数ψ 随涡轮机实际压力比B 的变化规律。由图4(a)可知，设计工况下i=β1n-β1=0°，符合涡轮机动叶栅设计要求;当B ＞Bs时，c1、u 均减小，且u 的变化速度因推进器的惯性作用而小于c1;由进口速度三角形可知，c1的减小起主导作用时β1增加，进而使气流撞击角i 为负，且随着c1的减小i 不断减小;同理，当B ＜Bs时，c1的变化起主导作用使得气流撞击角先增大而后减小。由i 的变化情况可分析速度因数ψ 的变化规律。当i ＞0°时，气流方向偏向叶型的凹面，此时有较大的气流冲击损失，对应图中i 处于最大正值时动叶栅速度因数取得最小值;当i ＜0°时，气流方向偏向叶型的凸面，此时的气流冲击损失将小于i ＞0°时的情况;i ＜0°时，速度因数ψ 随着i的减小呈现抛物线变化趋势，并在i = -1.42°时取得最大值ψ =0.849. 图4(b)给出了动叶栅轮周功Wu和轮周效率ηu随涡轮机实际压力比B 的变化规律。分析轮周功的计算公式Wu=u(w1× cos β1+w2cos β2n)可知，实际速度c1减小则w1、w2、u 均减小且β1增大，其共同作用致使Wu减小，故动叶栅轮周功Wu与喷嘴出口工质实际速度c1有相同的变化趋势;分析轮周效率的另一计算公式ηu=1 -(Δhn+Δhb+Δhe)/h*a 可知，喷嘴损失Δhn、动叶损失Δhb对ηu影响较大，也即动叶栅轮周效率ηu与喷嘴速度因数φ 和动叶栅速度因数ψ 密切相关;由φ、ψ 的变化趋势不难得到轮周效率ηu如图4(b)所示的变化趋势:设计压力比下ηu同φ 一样取得最大值;当B ＞Bs时，ψ 先增大后减小的作用致使ηu在Bs＜B ＜0.073 4 内下降速度低于φ，而后随着ψ 的减小，ηu下降速度增大;当B ＜Bs时，由于ψ 的减小使得ηu下降速度大于φ. 总体来讲，涡轮机轮周效率与喷嘴速度因数具有相同的变化规律。

由涡轮机动叶栅的仿真结果及分析可知，动叶栅各参数的变化规律反映了变工况下动叶栅的工作特性，进而验证了模型建立与仿真的正确性。

2.1.3 涡轮机热力特性计算结果及分析

考虑涡轮级能量损失模型，对压力比下涡轮机的热力特性进行计算，结果如图5所示。

图5 变压力比下涡轮机热力特性计算结果Fig.5 Thermal characteristic calculated results of turbine engine under changing pressure ratio

图5给出了涡轮机内效率ηi及其有效功率Pe随涡轮机实际压力比B 的变化规律。首先分析内效率ηi的变化规律，ηi在轮周效率ηu的基础上考虑了Δhfr、Δhl、Δhw、Δhs，由于这些损失并非涡轮级能量损失的主要部分，不改变轮周效率ηu的变化趋势，故内效率ηi与ηu、φ 具有相同的变化规律。其次分析有效功率Pe的变化规律，变压力比下ηm可视为定值，而内效率ηi与喷嘴速度因数φ 具有相同的变化规律，则涡轮机有效功率即喷嘴出口工质实际速度大小c1决定了涡轮机有效功率Pe的变化规律。

综合上述分析知，对于研究机型，变压力比下涡轮机喷嘴速度因数决定了涡轮机内效率及其轮周效率的变化规律，喷嘴出口工质实际速度决定了涡轮机有效功率及其轮周功的变化规律。

2.2 喷嘴入口温度变化时的涡轮机热力计算

利用建立的水下汽轮机变工况计算模型，对喷嘴入口工质温度Tc变化时的涡轮机热力特性进行仿真计算，得到设计背压p1=p1s和非设计背压p1分别为0.10 MPa、0.26 MPa 下涡轮机内效率ηi及其有效功率Pe的变化规律，如图6所示。

图6 喷嘴入口温度变化时的涡轮机热力计算结果Fig.6 Thermal characteristic calculated results of turbine engine along with temperature variation of nozzle entrance

由图6(a)可知，设计工况和非设计工况下涡轮机内效率ηi均随着喷嘴入口温度Tc的增加而近似线性减小，且减小量十分有限，可见涡轮机内效率对喷嘴入口工质温度不敏感。喷嘴入口温度由520 ℃增至580 ℃的过程中，不同工作背压p1下的涡轮机内效率变化量Δηi不同:当p1分别为0.10 MPa、p1s、0.26 MPa 时，Δηi分别对应0.003 03、0.002 70、0.002 63. 由此可知，当p1在一定范围内变化时，相同喷嘴入口温度变化量对应的涡轮机内效率变化量Δηi随p1的增大而减小。比较相同喷嘴入口温度、不同工作背压下的涡轮机内效率数值大小可知:设计工况下内效率最大，这是由于非设计工况下，喷嘴出口处存在膨胀波或激波，致使喷嘴速度因数下降，且由2.1 节变压力比下涡轮机内效率ηi的变化规律可知，喷嘴速度因数φ 减小必然导致非设计工况下内效率ηi的降低;相对设计背压p1s有相同压力变化量的两p1对应的ηi不相同，其中较小p1对应的内效率ηi更小。

由图6(b)可知，设计工况和非设计工况下涡轮机有效功率均随着喷嘴入口温度的增加而近似线性增加。喷嘴入口温度由520 ℃增至580 ℃的过程中，不同工作背压p1下的涡轮机有效功率变化量ΔPe不同:当p1分别为0.10 MPa、p1s、0.26 MPa 时，ΔPe分别为3.608 kW、3.447 kW、2.849 kW. 由此可知，当p1在一定范围内变化时，相同喷嘴入口温度变化量对应的ΔPe随p1的增大而减小。比较相同喷嘴入口温度、不同工作背压下的涡轮机有效功率数值大小知，p1越低涡轮机输出的有效功率越大，其原因在于工作背压降低，喷嘴出口工质实际速度增加，进而引起涡轮机有效功率增加。

3 结论

本文在建立水下涡轮发动机变工况热力特性计算模型的基础上，对某特种蒸汽涡轮发动机变压力比以及喷嘴入口工质温度变化时的热力过程开展仿真研究，得到如下结论:

1)文中建立的水下涡轮发动机变工况热力特性计算模型能够较好反映该型动力装置实际工作过程中的能量转化规律，可作为涡轮发动机动态特性研究的基础模型。

2)与喷嘴入口温度相比，涡轮机内效率对其压力比的变化更为敏感。

3)对于研究机型，变压力比下喷嘴速度因数决定了涡轮机内效率及其轮周效率的变化规律，喷嘴出口工质实际速度决定了涡轮机有效功率及其轮周功的变化规律。

References)

［1］ 赵坚，于明. 航空发动机涡轮盘振动模态与声模态分析研究［J］.兵工学报，2010，31(1):179 -183.ZHAO Jian，YU Ming. Vibrational and acoustic modal analyses of gas turbine disk in aeroengine［J］. Acta Armamentarii，2010，31(1):179 -183. (in Chinese)

［2］ 李磊，敖良波，李元生，等.船用高压比大流量增压器涡轮多学科设计优化［J］.兵工学报，2010，31(5):574 -579.LI Lei，AO Liang-bo，LI Yuan-sheng，et al. Multidisciplinary design optimization for marine supercharger turbo［J］. Acta Armamentarii，2010，31(5):574 -579. (in Chinese)

［3］ Osborne G F. The spearfish propulsion system［J］. GEC Review，1998，13(3):150 -162.

［4］ Rodriguez J M.A nonlinear model of a turbine blade by asymptotic analysis［J］. International Journal of Applied Mathematics and Compurter Science，2002，12(1):101 -113.

［5］ 聂卫东，赵宽明，孙开锋，等.鱼雷涡轮机数字仿真［J］.鱼雷技术，2007，15(4):14 -17.NIE Wei-dong，ZHAO Kuan-ming，SUN Kai-feng，et al. Digital simulation of torpedo turbine［J］. Torpedo Technology，2007，15(4):14 -17. (in Chinese)

［6］ 罗凯，党建军，王育才.涡轮发动机喷管出口速度的估计方法［J］.鱼雷技术，2009，17(1):44 -47.LUO Kai，DANG Jian-jun，WANG Yu-cai. Estimation method of nozzle exit speed for torpedo turbine engine［J］. Torpedo Technology，2009，17(1):44 -47. (in Chinese)

［7］ 练永庆，田兵，王树宗，等.空气涡轮泵发射系统发射过程仿真分析［J］.兵工学报，2011，32(2):155 -162.LIAN Yong-qing，TIAN Bing，WANG Shu-zong，et al. Simulation and analysis of the launching process of air-turbine pump launch system［J］. Acta Armamentarii，2011，32(2):155 -162. (in Chinese)

［8］ 练永庆，徐勤超，王树宗. 空气涡轮机带负载启动过程仿真［J］.机械工程学报，2011，47(8):191 -198.LIAN Yong-qing，XU Qin-chao，WANG Shu-zong. Simulation of startup process of air turbine with load［J］. Chinese Journal of Mechanical Engineering，2011，47(8):191 -198. (in Chinese)

［9］ 陈刚，伊进宝，师海潮.基于ANSYS CFX 的鱼雷涡轮机通流流场及性能计算方法［J］.鱼雷技术，2012，20(4):285 -294.CHEN Gang，YI Jin-bao，SHI Hai-chao. Numerical simulation of torpedo turbine flow passage field and performance using ANSYS CFX［J］. Torpedo Technology，2012，20(4):285 -294. (in Chinese)

［10］ Zhang F F，Zhang Z S，Zhu Rui. Optimization design study on a new type underwater turbine engine［J］.Advanced Materials Research，2014，850/851:292 -295.

［11］ 王保国，刘淑艳.气体动力学［M］. 北京:北京理工大学出版社，2005.WANG Bao-guo，LIU Shu-yan. Gas dynamics［M］. Beijing:Beijing Institute of Technology Press，2005. (in chinese)

［12］ Grkovic V R，Zivkovic D S，Gutesa M M.A new approach in combined heat and power stream turbine thermodynamic cycles computations［J］.Thermal Science，2012，16(2):399 -407.

［13］ 韩勇军，杨赪石，彭博.涡轮机动力系统变工况过程内效率建模与仿真［J］.鱼雷技术，2009，17(5):58 -62.HAN Yong-jun，YANG Cheng-shi，PENG Bo. Modeling and simulation of inner efficiency in non-design condition for torpedo turbine［J］. Torpedo Technology，2009，17(5):58 -62. (in Chinese)

［14］ 钱志博，曹伟.水下航行器燃气涡轮动力系统的多目标函数优化［J］.机械科学与技术，2006，25(1):91 -94.QIAN Zhi-bo，CAO Wei. Multiple optimization design for an underwater vehicle’s gas turbine propulsion system［J］. Mechanical Science and Technology，2006，25(1):91 -94. (in Chinese)

［15］ 赵寅生.鱼雷涡轮机原理［M］. 西安:西北工业大学出版社，1995.ZHAO Yin-sheng. Torpedo turbine principle［M］. Xi’an:Northwestern Polytechnical University Press，1995. (in Chinese)