等离子体射流点火对燃烧转爆轰影响的二维数值计算

林玲，翁春生

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

0 引言

脉冲爆轰发动机(PDE)是一种利用脉冲式爆轰波产生的高温、高压燃气来获得推力的新概念发动机，被认为是最具有发展前景的动力装置之一［1-2］。由于液体燃料便于携带，如何对气液两相爆轰进行快速点火起爆并形成稳定爆轰是PDE 走向工程应用急需解决的问题之一。

研究表明，射流火焰点火可以缩短燃烧转爆轰距离(DDT)，这种点火方式利用预燃室形成的射流火焰点燃爆轰管中的可燃混合［3-4］。王治武等［5］模拟了不同参数状态下横向射流在充满丙烷/空气化学当量比混合物的爆震室中起爆过程，分析了横向射流的起爆和机理。曾昊等［6］对氢气/空气混合物中爆震射流横向进入爆震室中的起爆过程进行了模拟，研究了不同联焰管位置及填充速度下横向射流的起爆特性。于军力等［7］通过乙炔/空气混合物的爆燃转爆轰实验表明射流点火可有效提高爆震管中火焰的初始速度。射流点火需要通过预燃方式来实现，结构比较复杂，而等离子体射流点火具有结构简单，点火能量大、脉冲放电时间短和能量转移效率高等优点，此技术已在化工、航天等领域得到了广泛应用，但是将其应用到气液两相爆轰的研究尚少。采用等离子射流点火起爆仍处于探索阶段，因此本文采用等离子射流点火起爆。

国内外学者对气液两相爆轰进行了大量理论研究。Cheatham 等［8］分别对空气和JP10 汽油建立Euler 方程和拉格朗日方程，对速度和压力等爆轰参数进行了数值模拟。张海波等［9］建立双流体模型，分别采用TVD 格式和MacComacke 格式计算气相和液相，对气液两相爆轰进行了数值计算。对于爆轰波的数值模拟，一般都采用Euler 方程作为控制方程，忽略了粘性作用对爆轰的影响。武丹等［10］采用N-S 方程作为控制方程对一维和二维连续旋转爆轰波进行了数值模拟，分析了粘性和热传导对于流场参数的影响。本文采用CE/SE 方法对粘性气液两相爆轰进行数值计算。CE/SE 方法最早由美国航空航天局的科学家Chang［11］提出，是近年来出现的一种新的计算格式，与传统的数值计算方法相比，具有精度高、计算格式简单及捕获激波等强间断能力强等独特优势，CE/SE 方法已成为计算爆轰等强间断问题的有效方法。张德良等［12］在最初提出的CE/SE 方法的基础上进行了改善，提高了其计算精度及稳定性。刘凯欣等［13］在Chang［11］的基础上提出了一种新的非结构网格下的划分方法，解决了CE/SE 方法网格限制问题。刘建文等［14］运用非结构网格CE/SE 方法来计算多管的单相爆轰流场问题。但采用CE/SE 方法计算等离子体与爆轰耦合问题，目前还未见到报道。

国内外对于PDE 气液两相爆轰的模拟大多未考虑粘性影响，本文在前人研究的基础上，将二维粘性CE/SE 方法应用到等离子体射流点火的多相爆轰模型中，分别以N-S 方程和Euler 方程为控制方程，比较了等离子射流点火条件下粘性作用对爆轰参数的影响。在此基础上分析了不同的等离子体射流初始点火温度、时间及初始液滴半径对燃烧转爆轰过程的影响。

1 多相爆轰模型及计算方法

1.1 计算模型及简化假设

图1为等离子体射流壁面点火的PDE 模型示意图。由于PDE 内流场爆轰过程为轴对称流动，只需计算一半区域，故采用二维计算模型即可。图1中RQ 以上部分为等离子体发生器，ORQP 所围成的区域为爆轰管上半平面，其中OR 为推力壁，RC'和CQ 为爆轰管壁面，PQ 为爆轰管出口，C'BC 为等离子体射流入口，OP 为中心对称轴。

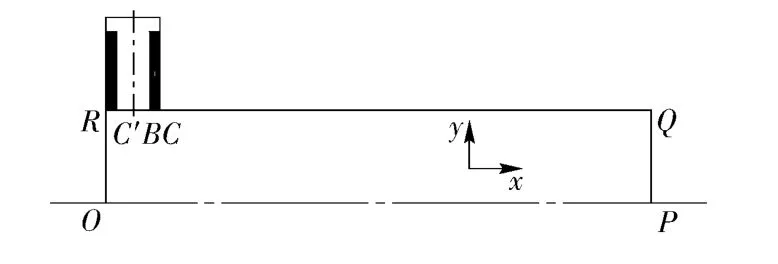
图1 等离子体射流壁面点火模型示意图Fig.1 Schematic diagram of wall plasma jet ignition model

在等离子体射流点火的爆轰内流场计算中，为了简化计算，提出以下假设:

1)PDE 管内多相爆轰过程为轴对称粘性过程;

2)将液滴颗粒群视为具有连续介质特性的拟流体;

3)初始及全过程液滴呈球形，大小均匀，液滴间无相互作用;

4)液滴剥离蒸发后成为气体，与气体瞬间均匀混合;

5)不考虑PDE 管壁与外界的热交换;

6)等离子体处于局域热力学平衡状态;

7)将等离子体作为气相中的一种组分，考虑它的质量和能量的变化，其速度与其他气相速度一致;

8)等离子体为光学薄，只辐射热量而不吸收热量。

1.2 控制方程

基于以上假设，得到等离子体射流点火的PDE内流场气液流动的轴对称粘性方程:

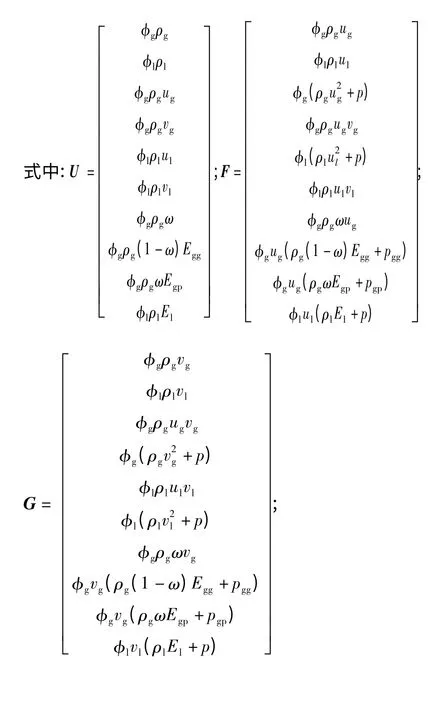
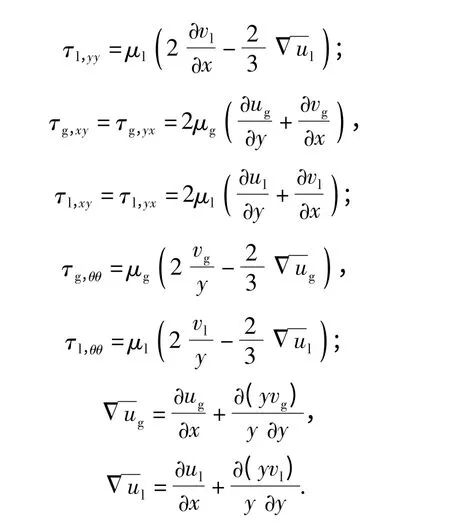
式中:τij(i、j =x，y，θ)，x、y、θ 分别代表柱坐标系下3 个不同方向，i=j 时表示正应力，i≠j 时表示剪切应力;下标g 和l 分别表示气相和液相;下标gp 和gg 分别表示气相中的等离子相和非等离子体相;ω表示等离子体在气相中的质量分数;φg和φl表示气相和液相的体积分数，满足φg+φl=1;u、v 分别表示x、y 方向的速度;ρ 为密度;p 为压力;T 为温度;E 是总能量，E =e +u2/2，e 为内能;Fdx、Fdy分别表示单位体积中气体对液滴的轴向、径向作用力;Qc为化学反应热;Qd为相间热传导;Qp为等离子体的辐射换热;rc为液滴半径;详细参数见文献［15］.

1.3 计算方法

本文将二维粘性CE/SE 方法应用到等离子体射流点火的多相爆轰计算中。CE/SE 方法推导是基于空间和时间通量守恒原理，是近年来出现的一种新的计算格式。二维粘性CE/SE 方法计算格式如下所示，具体推导过程见文献［16］.

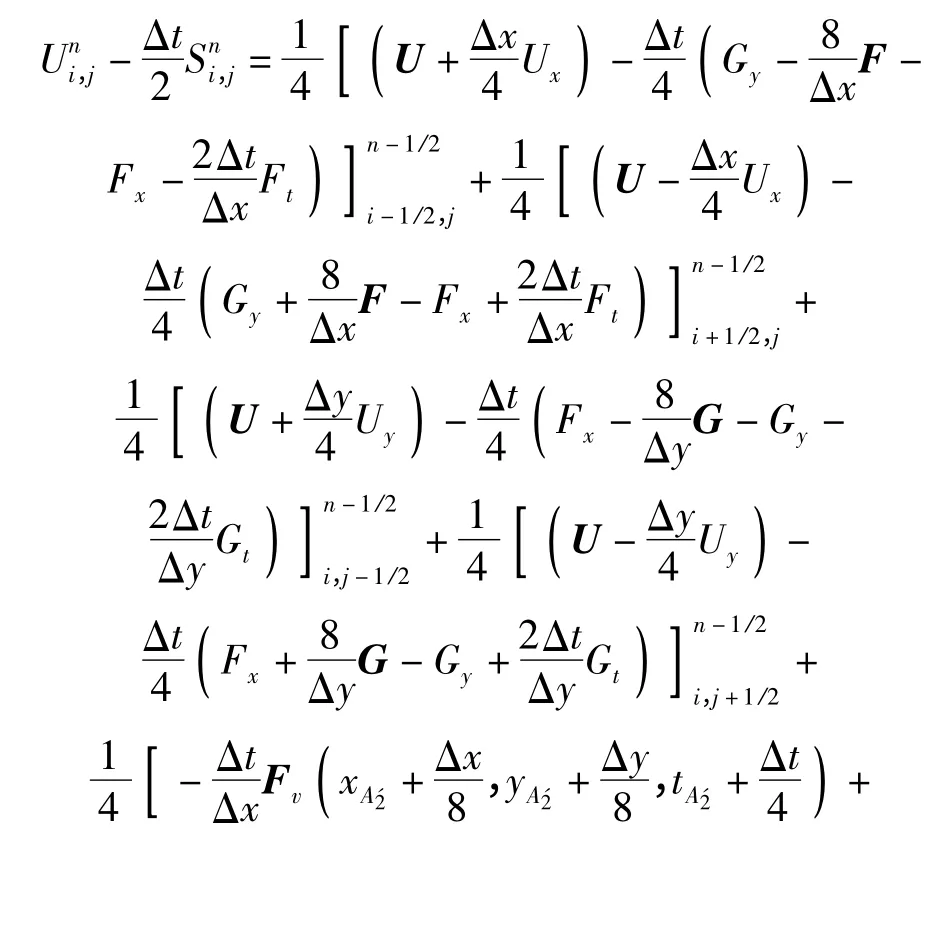
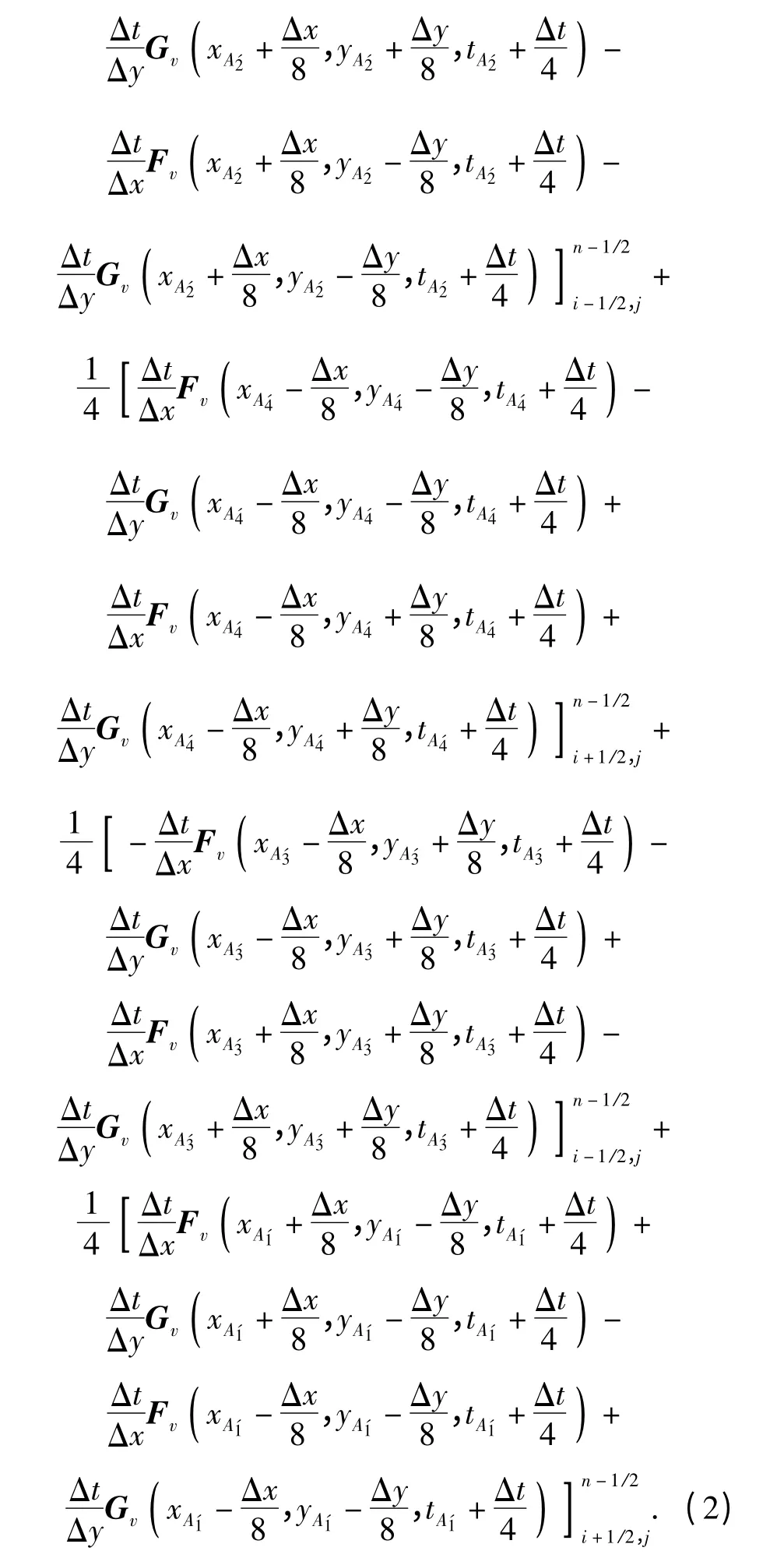
1.4 源项的处理

由于化学反应的特征时间远远小于对流的特征时间，故源项是刚性的。对于存在化学反应的源项，本文采用4 阶Runge-Kutta 法对源项进行处理。其求解思想:暂且不考虑源项，先采用CE/SE 方法求解出，再将作为初值，求解常微分方程组

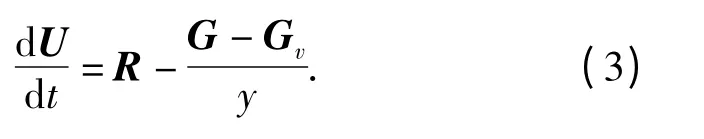
1.5 等离子体射流的计算

等离子体射流由耦合的流体力学方程和麦克斯韦方程求解［17］得到，本文采用二维CE/SE 方法对含有对流项和扩散项的磁流体动力学方程组进行了计算。

2 计算结果及其分析

2.1 初始条件与边界条件

初始条件:等离子体发生器内充满常温常压空气，空气在通电后电离形成等离子体。等离子体射流从孔C'C 段射入爆轰管进行点火。汽油/空气混合物按一定化学当量比均匀充满爆轰管内。爆轰波扫过后，汽油液滴剥离和蒸发，释放出能量。

边界条件:OP 段采用轴对称边界条件;PQ 段采用CE/SE 方法的非反射自由边界条件;RC'、CQ段均采用壁面反射边界条件。C'C 段边界条件在等离子射流点火期间采用等离子体发生器的出口参数，在射流停止后采用壁面反射边界条件。

2.2 粘性作用对爆轰参数的影响

计算中将等离子体射流从等离子体发生器喷嘴处射入爆轰管中，本文采用壁面点火方式，即等离子体射流位置处于爆轰管壁面的头部。为了研究探讨粘性对爆轰流场的作用，本文分别对粘性与无粘两种方式加以模拟，对比了在等离子体射流点火条件下粘性作用对爆轰参数的影响情况。

图2为等离子体射流点火不同时刻爆轰管内压力分布等值线图。等离子体射流开始后，等离子体射流带动并点燃部分汽油/空气混合物，等离子体以辐射的形式不断地将能量传递给气相工质。等离子体射流点火结束后在爆轰管壁端形成了一个稳定的高温区域，如图2(a)所示。周围的汽油液滴剥离蒸发后与空气混合物被高温气体迅速点燃，形成圆形压缩波并向未燃区域传播。压缩波由于左端推力壁的作用，受到推力壁的约束和挤压后向右传播。压缩波继续传播在t=67.3 μs 时刻与下壁面发生碰撞后形成高压区域(p =6.57 MPa)，并反射形成一个向上传播的横波如图2(b)所示。当横波继续传播在t=130.0 μs 时刻到达上壁面时再次发生反射，形成一个向下传播的反射波，如图2(c)所示。当激波达到下壁面时又会再次发生反射，反射波的上下运动会加快未反应区混合物的化学反应速率，从而不断的增强前导激波的强度，最终形成横向充满整个爆轰管的爆轰波(图2(d)所示，t =271.0 μs 时开始形成稳定爆轰波，p=1.68 MPa).

图2 不同时刻爆轰管内压力分布等值线图(有粘)Fig.2 Contour plots of pressure in detonation tube at different moments (viscous)

图3为不同时刻管壁压力随x 轴向分布曲线。其中图3(a)为考虑粘性的压力分布曲线图，图3(b)为未考虑粘性的压力分布曲线图。由图3可以看出，随着时间的推移，压力峰值不断上升后趋于稳定。由于局部高压点经过，曲线3 压力峰值上升速率加快。图3中可以看出曲线5 处压力峰值(p=1.68 MPa)趋于稳定，说明此时已经形成了稳定的爆轰波。本文定义从点火时间到爆轰波压力值达到最高稳定压力峰值的97%，且之后爆轰波压力值均在此范围内波动的时间为DDT 时间。从点火位置到爆轰波压力值达到最高稳定压力峰值的97%，且之后爆轰波压力值均在此范围内波动的位置为DDT 距离。图3(a)中形成稳定爆轰波压力峰值达到1.68 MPa，DDT 时间为296.3 μs;图3(b)中形成稳定爆轰波的压力峰值达到1.76 MPa，DDT 时间为304.30 μs.

图4为不同时刻管壁轴向速度分布曲线。图4(a)为考虑粘性的轴向速度曲线图，图4(b)为未考虑粘性的轴向速度曲线图。由图4可以看出，随着时间的推移，速度值不断上升后趋于稳定。图4(a)中形成稳定爆轰波的气相速度值达到894 m/s，图4(b)中形成稳定爆轰波的气相速度值达到927 m/s.

分析图3和图4可知，考虑或不考虑粘性作用爆轰波的传播过程基本相同，压力变化与气相速度变化规律一致。管壁处由于粘性作用，爆轰波传播过程中阻力增大，能量有所损失，从而速度减小，爆轰波传播强度降低。粘性作用不会影响爆轰波的传播趋势，仅对爆轰波传播强度和速度有所影响。因此采用考虑粘性的等离子体射流点火的爆轰模型可以更真实地反映燃烧转爆轰的特性。

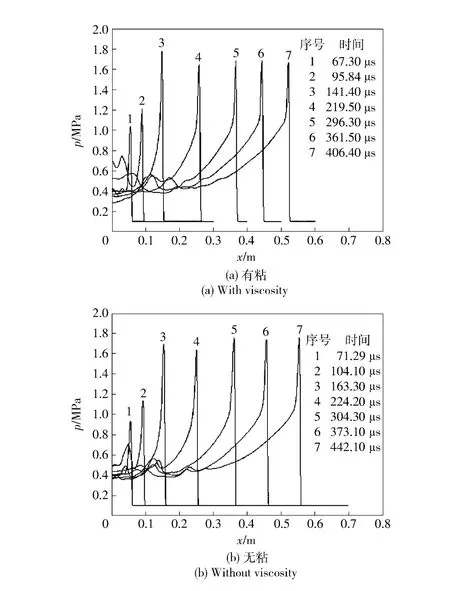
图3 管壁压力随x 轴向分布曲线Fig.3 Distribution curves of wall pressure along x axis

2.3 初始射流点火温度和时间对燃烧转爆轰的影响

根据2.2 节的研究结果本节采用带粘性项的N-S 方程对等离子体射流点火的多相爆轰进行了数值研究，考虑了等离子体点火的初始射流温度、射流时间对燃烧转爆轰的影响。图5为不同等离子体射流点火温度和时间在形成稳定爆轰波管壁位置处峰值压力随x 轴变化曲线图。图5中可以看出:当射流温度T 为5 000 K 时，射流时间t=500 ns，DDT 距离x=0.439 m;射流时间t=1 000 ns，DDT 距离x=0.427 m;射流时间t = 2 000 ns，DDT 距离x=0.425 m.可以看出随着射流时间的增加，形成稳定爆轰时的DDT 距离在减小，且减小的幅度(2.73%下降为0.47%)不断降低，峰值压力(p=1.9 MPa 左右)则基本不变。由此可见初始的等离子体射流时间并不能影响形成稳定爆轰波压力峰值的大小。当初始点火的等离子体射流已经充分点燃可爆混合物，继续增加射流时间对缩短DDT 距离作用不明显。当射流时间为1 000 ns，射流温度T =5 000 K，DDT 距离x =0.427 m;射流温度T =4 000 K，DDT距离x=0.457 m. 温度为5 000 K 时形成稳定爆轰的DDT 距离较4 000 K 时缩短了6.6%，说明提高初始射流温度可以显著地缩短DDT 距离。

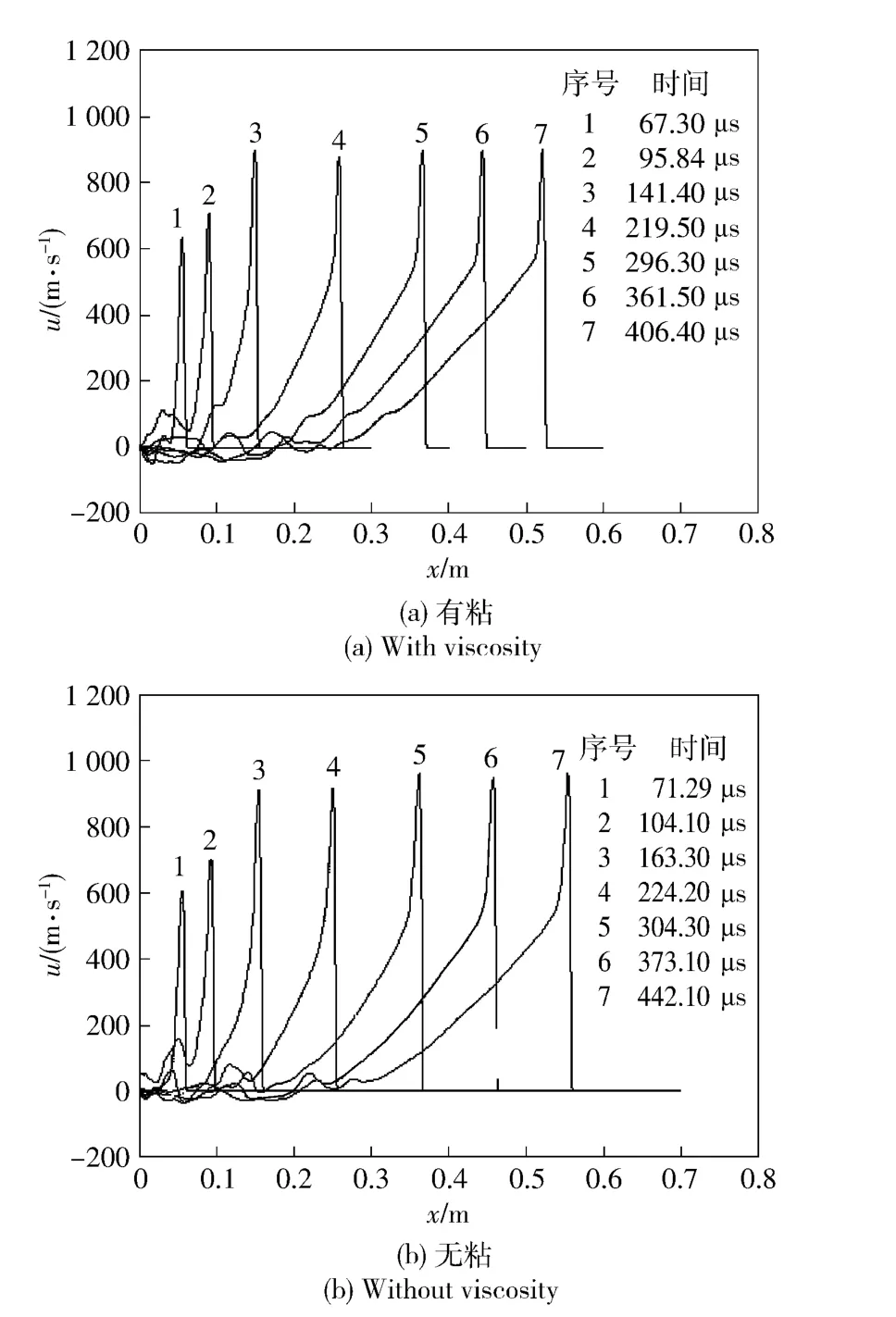
图4 管壁轴向速度分布曲线Fig.4 Distribution curves of wall velocity along x axis

2.4 初始液滴半径对燃烧转爆轰的影响

为了进一步研究初始液滴半径对燃烧转爆轰的影响，本文采用二维粘性CE/SE 方法对不同初始液滴半径在一定的等离子体射流点火条件下的燃烧转爆轰情况进行了研究。

由表1中可以看出:初始液滴半径小于50 μm时，随着液滴半径的增大，爆轰压力峰值增大;液滴半径大于50 μm 时，随着液滴半径的增大，爆轰压力峰值减小。而形成稳定爆轰的DDT 时间和距离则一直随着初始液滴半径的增大而增大。液滴半径50 μm，达到最大的压力峰值(p =1.90 MPa). 气体和液滴间的相互作用主要有液滴边界层的剥离效应和温差引起的蒸发效应。液滴半径越大，同一位置处燃料液滴剥离和蒸发所需时间越长。在化学当量比一定的汽油/空气混合物中，随着液滴半径的增加，单位体积内液滴数目减少，与空气中氧气接触的总面积则变小，化学反应强度则会减弱，释放出的能量减少。爆轰波传播过程中所持能量强度减弱，形成稳定爆轰波所需的能量积聚的时间增加，则得到稳定爆轰波的时间增加。液滴半径大于150 μm，不能形成稳定爆轰波。这是由于液滴半径过大，液滴剥离和蒸发的时间过长，会大大降低燃料蒸汽与氧气发生化学反应的效率，不利于燃料的充分燃烧，从而导致释放的能量过小不能够补偿激波传播所需的能量，故不能够形成爆轰。

图5 不同射流点火温度和时间达到稳定爆轰波管壁位置处的p-x 曲线图Fig.5 Curve chart of p-x at different ignition temperatures and time of jet

表1 不同初始液滴半径对爆轰参数的影响Tab.1 Effect of initial droplet radius on detonation

3 结论

本文采用二维粘性CE/SE 方法对等离子射流点火的多相爆轰模型进行了数值计算，通过以N-S方程和Euler 方程为控制方程，对比了等离子体射流点火条件下考虑粘性作用时爆轰参数的变化情况。在此基础上，分析了不同射流点火温度及初始液滴半径对燃烧转爆轰过程的影响。计算结果表明:

1)粘性作用对爆轰波的传播过程影响甚小，对爆轰参数数值大小有一定影响。

2)提高初始点火射流的温度和时间，可以显著地缩短形成稳定爆轰的DDT 距离，当等离子体射流已经充分点燃可爆混合物，继续增加射流时间对缩短DDT 距离影响较小。

3)在等离子射流温度为5 000 K、射流时间为1 000 ns点火条件下:当液滴半径小于50 μm 时，随着液滴半径的增加，爆轰波峰值压力增加;当液滴半径大于50 μm 时，随着液滴半径的增加，爆轰波峰值压力减小。

References)

［1］ Dean A J. A review of PDE development for propulsion applications［C］∥45th AIAA Aerospace Science Meeting and Exhibit.Reno，Nevada:AIAA，2007 -985.

［2］ 严传俊，何立明，范玮，等. 脉冲爆震发动机的研究与发展［J］. 航空动力学报，2001，16(3):212 -217.YAN Chuan-jun，HE Li-ming，FAN Wei，et al. Research and development of pulse detonation engines［J］. Journal of Aerospace Power，2001，16(3):212 -217. (in Chinese)

［3］ Shimada H，Kenmoku Y，Saro H，et al. A new ignition system for pulse detonation engine［C］∥42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada:AIAA，2004:2004 -308.

［4］ 牟乾辉，胡宗民，赵伟，等. PDE 热射流起爆机理数值分析［J］. 计算物理，2005，23(3):266 -272.MU Qian-hui，HU Zong-min，ZHAO Wei ，et al. Numerical analyses of direct detonation initiation in PDEs with a precombustion jet［J］. Chinese Journal of Computational Physics，2005，23(3):266 -272. (in Chinese)

［5］ 王治武，陈星谷. 横向射流起爆爆震波数值研究［J］. 推进技术，2013，34(3):422 -427.WANG Zhi-wu，CHEN Xing-gu. Numerical investigation of the transverse jet effects on detonation initiation characteristics［J］.Journal of Propulsion Technology，2013，34(3):422 -427. (in Chinese)

［6］ 曾昊，何立明. 横向爆震射流起爆爆震过程的数值模拟［J］.应用力学学报，2010，27(3):543 -548.ZENG Hao，HE Li-ming. Simulation of transverse detonation jet initiation process［J］. Chinese Journal of Applied Mechanics，2010，27(3):543 -548. (in Chinese)

［7］ 于军力，秦亚欣，高歌. 射流点火对爆震管中爆燃转爆震影响的实验［J］. 航空动力学，2011，26(5):1043 -1047.YU Jun-li，QIN Ya-xin，GAO Ge，et al. Experimental investigation on effects of flame jet ignition on deflagration to detonation transition in tube［J］. Journal of Aerospace Power，2011，26(5):1043 -1047. (in Chinese)

［8］ Cheatham S，Kailasanath K. Multiphase detonations in pulse detonation engines［C］∥42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada:AIAA，2004，2004 -306.

［9］ 张海波，白春华，丁薇. 气液两相爆轰的数值模拟［J］. 兵工学报，2000，21(2):119 -1225.ZHANG Hai-bo，BAI Chun-hua，DING Wei ，et al. Numerical simulation for two-phase gas-droplet detonation［J］. Acta Armamentarii，2000，21(2):119 -1225. (in Chinese)

［10］ 武丹，王健平. 粘性及热传导对于爆轰波的影响［J］. 应用力学学报，2012，29(6):630 -635.WU Dan，WANG Jian-ping. Influences of viscosity and thermal conductivity on detonation waves［J］. Chinese Journal of Applied Mechanics，2012，29(6):630 -635. (in Chinese)

［11］ Chang S C. The method of space-time conservation element and solution element—a new approach for solving the Navier-Stokes and Euler equations［J］. Journal of Computational Physics，1995，119(2):295 -324.

［12］ 张德良，王景焘，王刚. 高阶精度CE/SE 算法及其应用［J］.计算物理，2009，26(2):211 -220.ZHANG De-liang，WANG Jing-tao，WANG Gang. High-order CE/SE method and applications［J］. Chinese Journal of Computational Physics，2009，26(2):211 -220. (in Chinese)

［13］ Fu Z，Liu K X. An improved two-dimensional unstructured CE/SE scheme for capturing shock waves［］. Chinese Physics B，2012，21(4):040202.

［14］ 刘建文，赵书苗，钟诚文，等. CE/SE 方法在多管爆轰流场并行计算中的应用［J］. 爆炸与冲击，2008，28(3):229 -235.LIU Jian-wen，ZHAO Shu-miao，ZHONG Cheng-wen，et al.CE/SE scheme applied in parallel computation of PDE flow field［J］. Explosion and Shock Waves，2008，28(3):229 -235.(in Chinese)

［15］ 彭振，翁春生. 等离子体点火对PDE 一维两相爆轰影的数值计算［J］. 火炮发射与控制学报，2009 (2):77 -80.PENG Zhen，WENG Chun-sheng. Numerical calculation of influence of plasma ignition on PDE one-dimensional two-phase detonation［J］. Journal of Launch ＆Control，2009(2):77 -80. (in Chinese)

［16］ 翁春生，王浩. 计算内弹道［M］. 北京:国防工业出版社，2006:276 -290.WENG Chun-sheng，WANG Hao. Computational interior ballistics［M］. Beijing:National Defense Industry Press，2006:276 -290. (in Chinese)

［17］ 李昕，翁春生. CE/SE 方法模拟等离子体电枢二维MHD 效应［J］. 工程力学，2009，26(10):240 -251.LI Xin，WENG Chun-sheng. The 2-D MHD effect of plasma armature simulated by CE/SE method［J］. Engineering Mechanics，2009，26(10):240 -251. (in Chinese)