捷联成像导引头隔离度寄生回路及其内部动力学影响研究

郑多，林德福，宋韬，祁载康

(北京理工大学 宇航学院，北京100081)

0 引言

捷联导引头取消了机械运动部分直接固联在弹体上，与传统的导引头相比，捷联导引头视线跟踪角速率不受限制，消除俯仰/方位通道摩擦导致的交叉耦合，同时制导控制系统共用一组高精度惯性测量元件，使得系统结构复杂性和成本降低［1］。在捷联体制中，弹体运动信息完全耦合进导引头输出信号，为了隔离弹体运动，需要采用数学平台对弹体运动进行解耦，然而刻度尺系数误差、导引头延时和惯性器件动力学的存在影响弹体解耦精度，引起隔离度寄生回路问题。

关于寄生回路问题，文献［2 -3］提出了雷达天线罩误差引起寄生回路概念，并且文献［3］中详细分析了天线罩斜率误差引起的隔离度对寄生回路稳定性及其脱靶量的影响。杜运理等［4］基于平台导引头提出了隔离度寄生回路问题，并分析了寄生回路稳定性。Mehra 等［5］基于空空导弹主动雷达捷联导引头提出捷联导引头刻度尺系数误差概念，并探讨使用扩展卡尔曼滤波估计刻度尺系数误差，然而并未深入研究制导系统参数对隔离度寄生回路稳定域的影响。Willman 等［6］将捷联导引头刻度尺系数误差作为不确定扰动，研究如何进行制导控制系统设计增加其抗扰动能力。Jang 等［7］研究了近程导弹克服隔离度寄生回路的制导律设计方法，并提出使用α-β 滤波器估计弹目视线角速度。综上所述，国内文献关于导引头隔离度寄生回路的研究主要围绕平台稳定式导引头展开［4，8-9］，国外文献主要研究了基于捷联制导体制的刻度尺系数误差估计补偿、克服寄生回路制导律设计等问题，几乎没有针对捷联成像导引头隔离度寄生回路研究的相关资料。

针对上述问题，本文分析了捷联成像导引头隔离度寄生回路产生的原因，建立了刻度尺系数误差、导引头相位滞后引起的隔离度寄生回路模型，研究了隔离度寄生回路不同剩余制导时间、内部动力学对稳定域的影响，给出了捷联导引头相位滞后引起隔离度寄生回路临界稳定的导引头延时与制导时间常数之间的关系，同时研究了在相同制导时间常数下，隔离度水平及其制导系统内部动力学对制导系统脱靶量的影响。通过分析，给出了捷联红外成像导引头工程应用的建议，可为导弹总体初步方案论证工作提供理论参考。

1 捷联成像导引头的隔离度问题

弹体姿态运动耦合进导引头输出信号的问题称为隔离度问题。故隔离度可以描述［4］为

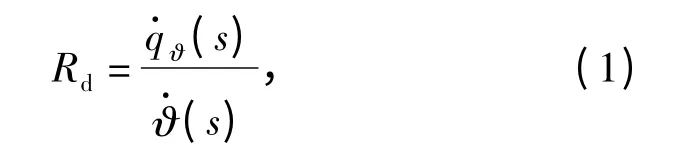
式中:Rd表示隔离度(s)为弹体姿态角速度引起的导引头输出弹目视线角速度;(s)为弹体姿态角速度。导致捷联导引头隔离度问题的原因很多，刻度尺系数误差、导引头相位滞后和惯性器件动力学都会不同程度地引起导引头隔离度问题。本文主要对刻度尺系数误差和导引头延时引起的隔离度寄生回路的影响进行研究。捷联成像导引头的弹目几何关系如图1所示。

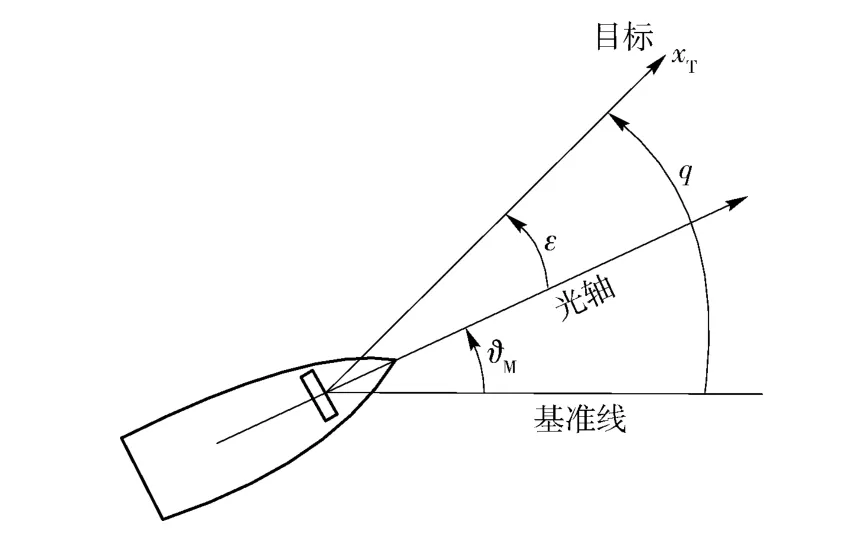
图1 捷联成像导引头弹目关系Fig.1 Missile-target relationship of strapdown imaging seeker

由图1可知，捷联导引头测角可表示为

式中:q 为惯性系下弹目视线角;ϑM为弹体姿态角;ε 为导引头测得的弹体视线角。则解耦表达式为

式中:q*为解耦得到惯性弹目视线角;ϑgyro为姿态陀螺测得弹体姿态角。

根据以上描述，对隔离度问题做如下定义:

由于刻度尺系数误差的存在，同一时刻姿态陀螺测得弹体姿态θtkgyro和耦合进导引头的实际弹体姿态值θtkM不相等，即ϑtkgyro≠ϑtkM，导致弹体姿态信息部分耦合进入制导信息而引起的隔离度问题称为刻度尺系数误差引起的隔离度寄生回路问题［8］。

由于导引头相位滞后的存在，捷联导引头测量信息和姿态陀螺测得弹体姿态信息在相位上不一至，即ϑtkgyro≠ϑtk+τM，导致弹体姿态运动耦合进入制导信息而引起的隔离度问题称为导引头相位滞后引起的隔离度寄生回路问题。

图2给出捷联红外导引头的制导控制系统框图。其中:tgo为剩余制导时间;vc为弹目相对速度;vm为导弹飞行速度;Tα为攻角滞后时间常数;ks为导引头刻度尺系数;kg为姿态陀螺刻度尺系数;τ 为导引头延时;ε 为导引头测得的弹体系下的弹目视线角;ϑgyro为弹体姿态角，由姿态陀螺测量得到，融合导引头和姿态陀螺的测量信息，再通过微分滤波网络即可得到比例导引所需的弹目视线角速度。

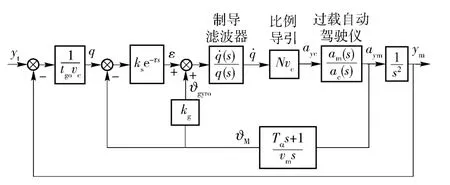
图2 捷联红外成像导引头制导系统模型Fig.2 Guidance system model of strapdown imaging seeker

在制导滤波器理想条件下，可以将其等效为微分环节，可等效变换为图3形式。

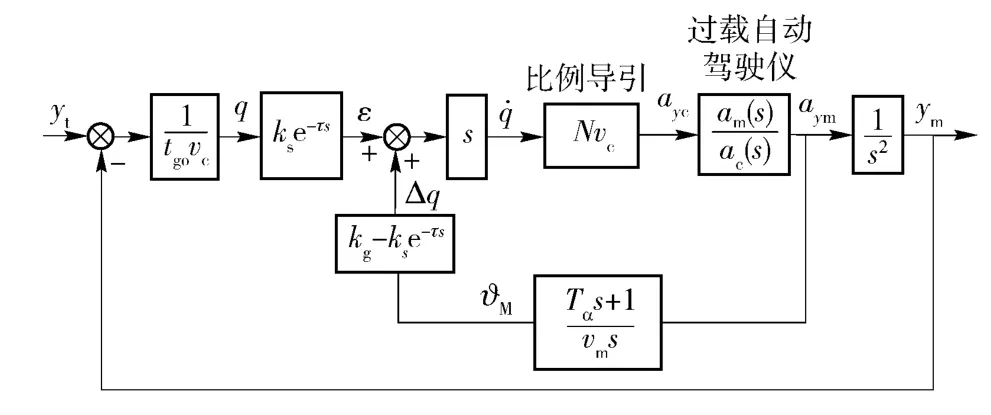
图3 捷联成像导引头隔离度寄生回路模型Fig.3 Parasitic loop model of strapdown imaging seeker

由图3可知，弹体姿态角速度引起的弹目视线角速度为

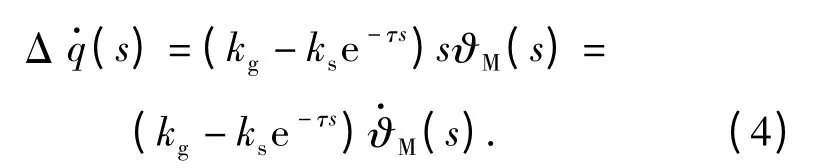
定义隔离度为

定义A(·)为求传递函数等效增益符号，则由(5)式和图3可知，隔离度A(Rd)的符号决定了隔离度寄生回路反馈的正负号。A(Rd)＜0 时，隔离度寄生回路的反馈回路是负反馈;A(Rd)＞0 时，隔离度寄生回路的反馈回路是正反馈。

从控制系统的角度分析，正反馈和负反馈对控制系统的稳定性的影响是不同的。

2 隔离度寄生回路稳定性研究

2.1 刻度尺误差引起的隔离度寄生回路

研究刻度尺系数误差引起的隔离度问题时，假设捷联导引头延时τ =0 s，则刻度尺系数误差引起的隔离度可表示为

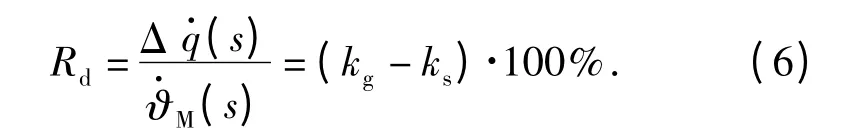
可得捷联成像导引头刻度尺系数误差引起的隔离度寄生回路框图，如图4所示。

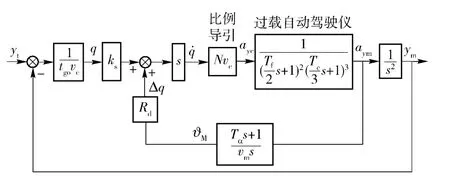
图4 刻度尺误差隔离度寄生回路模型Fig.4 Model of parasitic loop caused by scale factor error

图4给出了基于比例导引的隔离度寄生回路模型，其中:N 为有效导航比;vc为弹目相对速度;vm为导弹飞行速度;Tα为攻角滞后时间常数;在初步分析中，制导滤波器以2 阶动力学表示，Tf为制导滤波器常数;过载自动驾驶仪以3 阶动力学［2］表示;Tc为过载自动驾驶仪等效时间常数;制导时间常数可近似表示为Tg=Tf+Tc. 寄生回路内部动力学的不同描述为:当制导时间常数Tg保持不变时，Tf与Tc比值的改变导致内部动力学的不同。由图4可得导引头寄生回路传递函数为

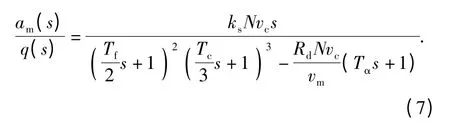
求得隔离度寄生回路制导系统闭环传递函数为

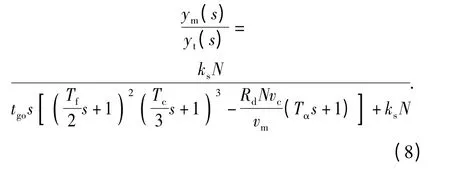
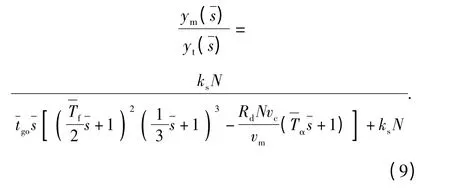
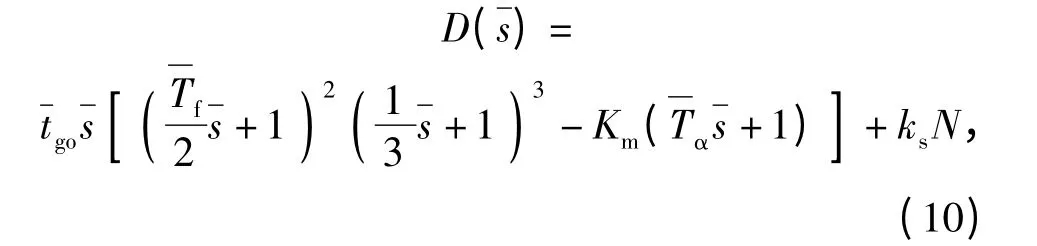
1)当Km＞0 时，寄生回路为正反馈，其稳定条件为

2)当Km＜0 时，寄生回路为负反馈，其稳定条件为

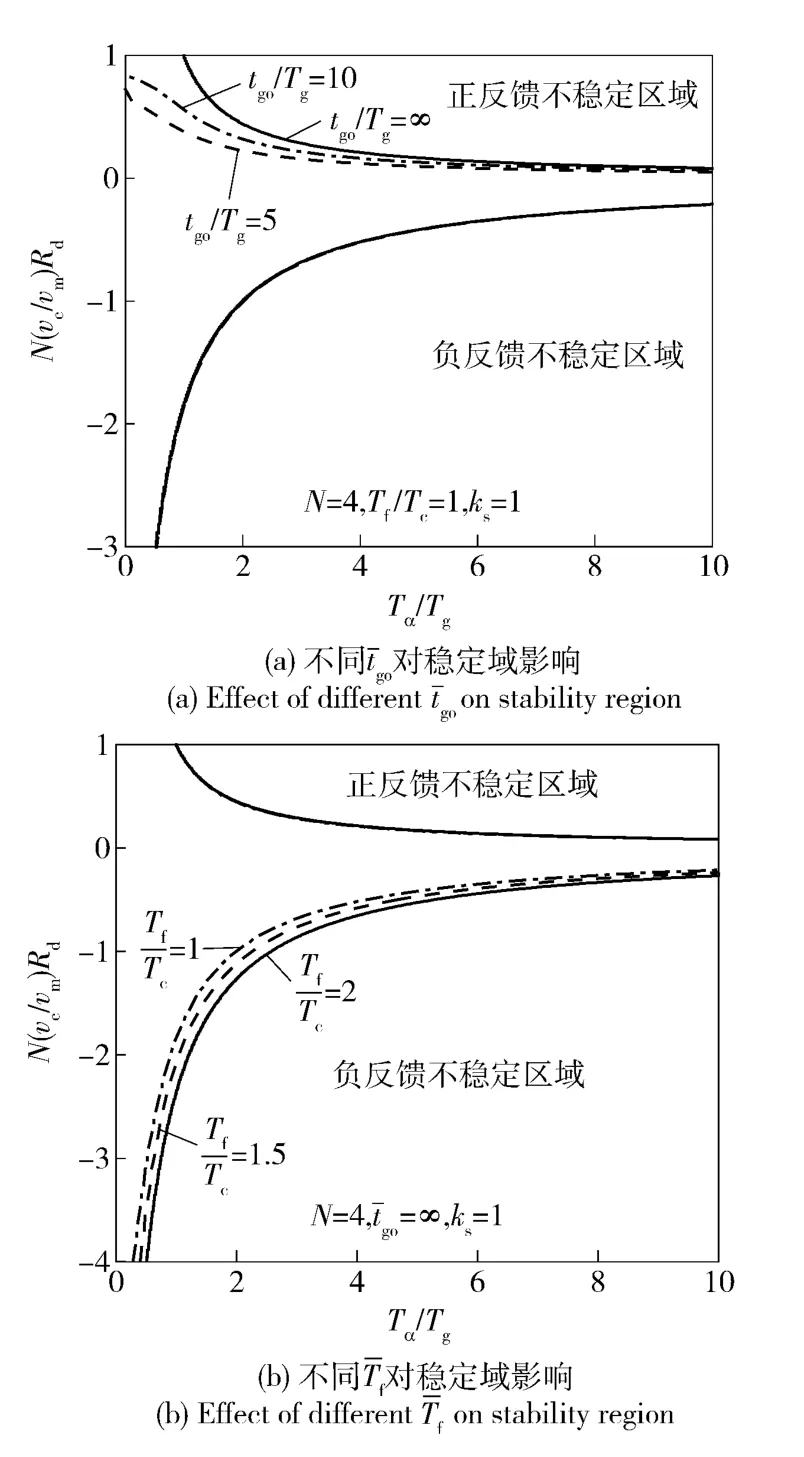
图5 无量纲隔离度寄生回路制导系统稳定域Fig.5 Stability regions of dimensionless disturbance rejection rate parasitic loop of guidance system

由图5可知，负反馈的稳定域大于正反馈的稳定域。稳定域随着Tα/Tg和N(vc/vm)Rd的增大而减小。由图5(a)可知，随着制导剩余时间的减小，正反馈的稳定域减小。由图5(b)可知，Tα/Tg越小，制导滤波器动力学时间常数Tf/Tc越大，负反馈稳定域越大，越不易失稳。由此可知，隔离度对寄生回路稳定性影响较大，正反馈稳定域明显小于负反馈稳定域，且随着制导剩余时间的减小而减小。负反馈稳定域受到制导系统内部动力学结构的影响，可通过改变Tf/Tc增大稳定域。因此，捷联导引头实际工程应用中，应该严格控制隔离度大小，尤其是寄生回路正反馈隔离度的大小。同时应通过气动优化设计使得攻角时间常数Tα尽量小，或者通过制导控制系统设计在制导时间允许的范围内增大制导系统系统时间常数Tg，以保证Tα/Tg尽可能小。在制导时间常数和攻角时间常数固定后，在设计捷联制导控制系统时，应尽量使得Tf/Tc大些，可在一定程度上增大负反馈的稳定域。

2.2 导引头相位滞后引起的隔离度寄生回路

研究捷联成像导引头相位滞后引起的隔离度寄生回路问题时，假设刻度尺系数ks=kg=1，则导引头相位滞后引起隔离度可表示为

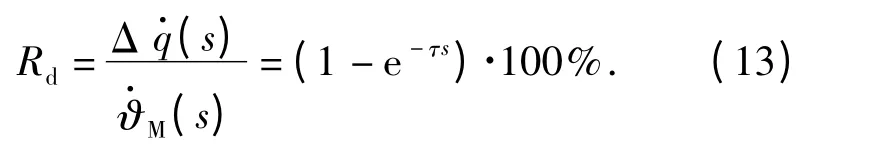
根据(13)式隔离度的定义，导引头相位滞后引起的隔离度寄生回路制导系统框图如图6所示。

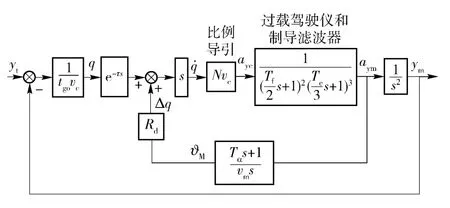
图6 导引头相位滞后引起的隔离度寄生回路Fig.6 Parasitic loop model caused by seeker phase lag

图6给出了导引头相位滞后引起隔离度制导系统稳定边界τ/Tg、Tf/Tc和Tα/Tg的关系。仿真结果表明:Tα/Tg减小，制导系统临界稳定的τ/Tg增大;Tα/Tg保持不变时，增大或减小Tf/Tc，制导系统临界稳定的τ/Tg几乎不变。因此，捷联成像导引头的实际应用中应尽量减小图像处理造成的导引头延时，在此基础上尽量减小攻角时间常数Tα/Tg.

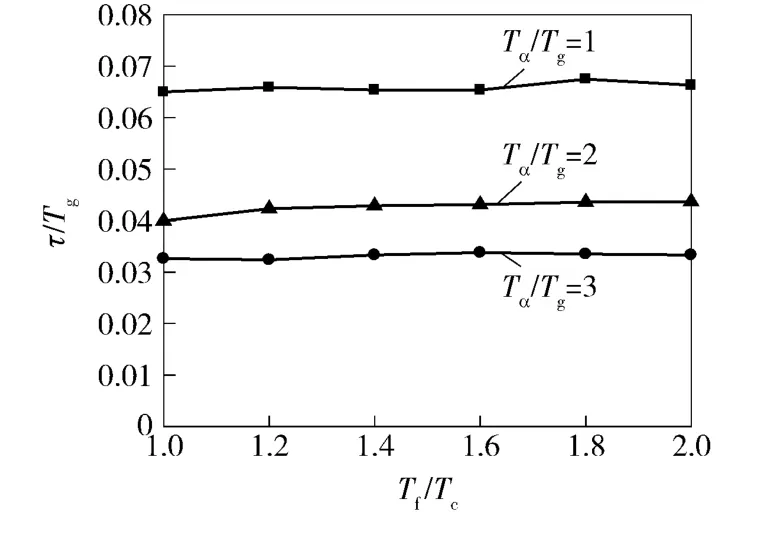
图7 相位滞后引起的隔离度制导系统稳定边界Fig.7 Stability boundary of parasitic loop guidance caused by seeker phase lag

为了研究隔离度寄生回路的开环幅频特性，假设制导剩余时间常数足够长，即tgo=∞，则可进一步简化比例导引制导系统模型，见图8.

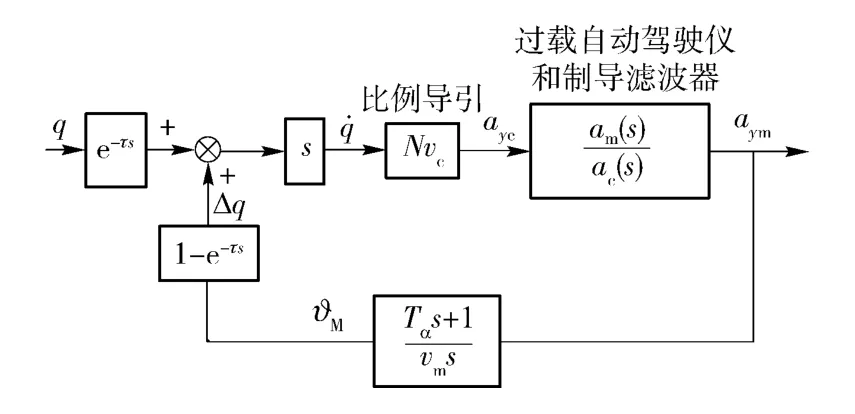
图8 隔离度寄生回路模型Fig.8 Parasitic loop model

前向通道的e-τs并不会影响寄生回路稳定性，可以忽略。令进行无量纲化处理，可得图9形式。

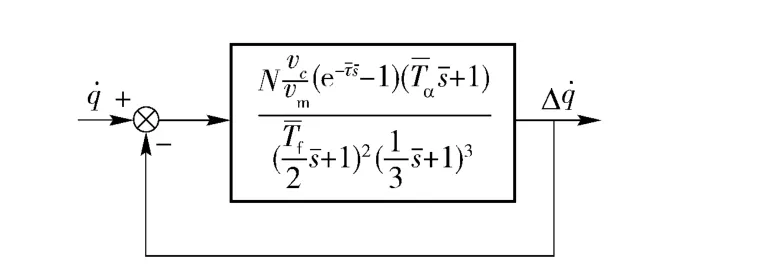
图9 无量纲隔离度寄生回路Fig.9 Dimensionless parasitic loop mode

由图9可知，捷联导引头相位滞后引起的隔离度寄生回路无量纲开环传递函数为

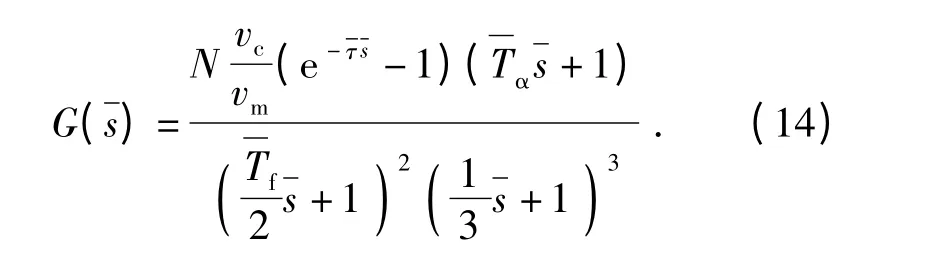
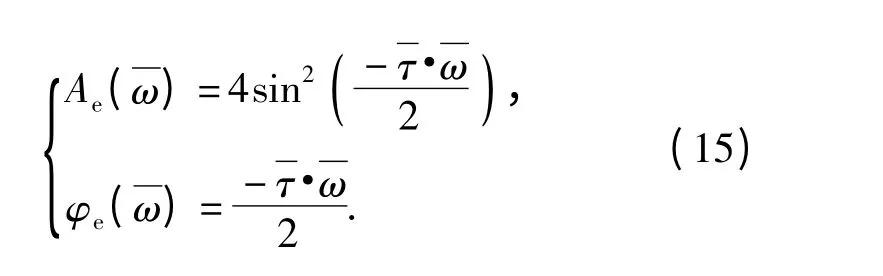
隔离度寄生回路开环无量纲传递函数的频率特性为

根据对数稳定判据，系统临界稳定的条件为

隔离度寄生回路开环幅值和相位曲线如图10所示。

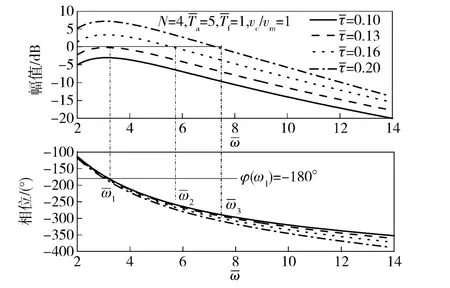
图10 隔离度寄生回路开环幅值相位曲线Fig.10 Amplitude and phase curves of parasitic loop

3 对制导系统的影响研究

由于隔离度寄生回路的存在，弹体姿态信息耦合进比例导引制导信息，导致导弹做“不必要”的机动，从而在噪声和干扰的作用下影响导弹制导系统精度，即脱靶量［11］。以下分析隔离度对脱靶量的影响，对制导系统典型干扰定义见表1［12］.

在本节研究中，Rd表示为隔离度(kg-kse-τs)的等效增益，以下不再赘述。将建立的干扰模型带入存在隔离度寄生回路的5 阶制导控制系统动力学模 型 中，并 且 建 立 无 量 纲 伴 随 模 型［2］，如图11所示，在存在隔离度寄生回路的情况下，分析不同干扰对制导精度的影响，其中，无量纲末制导时间=tF/(Tc+Tf).

图11 无量纲伴随系统框图Fig.11 Adjoint simulation model of guidance system

根据无量纲化的定义，无量纲脱靶量有如下转换关系，

定义无量纲脱靶量为

将(20)式带入(21)式、(22)式中可得

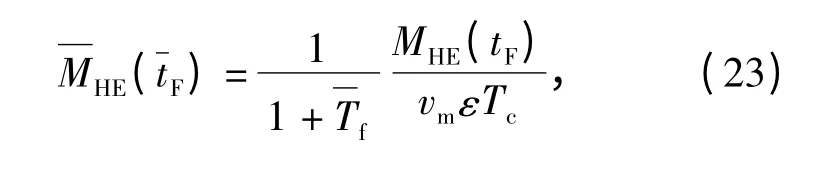
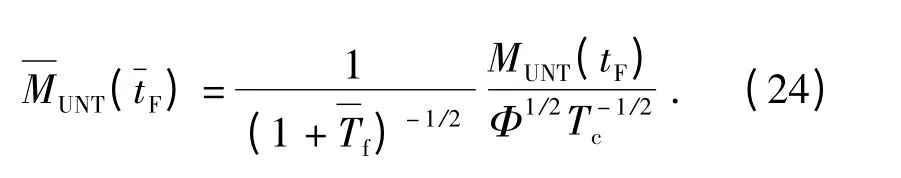
受隔离度寄生回路的影响，在初始速度偏差和探测器角噪声干扰作用下比例导引的脱靶量随末导时间的收敛情况将发生变化。为保证寄生回路不失稳，仿真条件选取N=4，Tf/Tc=1，Tα/Tc=8，vc/vm=1.0，ks=1，Rd分别取0%、±1%、±2%、±3%，仿真结果如图12所示。当隔离度Rd=0%时，脱靶量可以在tF=10Tg内收敛。当Rd≠0%时，正反馈对脱靶量的影响比负反馈大，脱靶量受负反馈影响较小，在初始速度方向偏差干扰作用下，增大末导时间，正反馈和负反馈情况脱靶量均可以收敛到0，负反馈需用末导时间比正反馈小。在探测器角噪声干扰作用下，正反馈情况下的脱靶量将增大，负反馈情况下脱靶量减小。总体而言，脱靶量随着隔离度水平的增大而加大，需用末导时间增长。综上所述，在隔离度寄生回路存在的情况下，正反馈对制导系统的性能影响要比负反馈严重，实际工程应用中，应该尽可能地避免隔离度寄生回路正反馈情况的出现，并且严格控制隔离度水平。

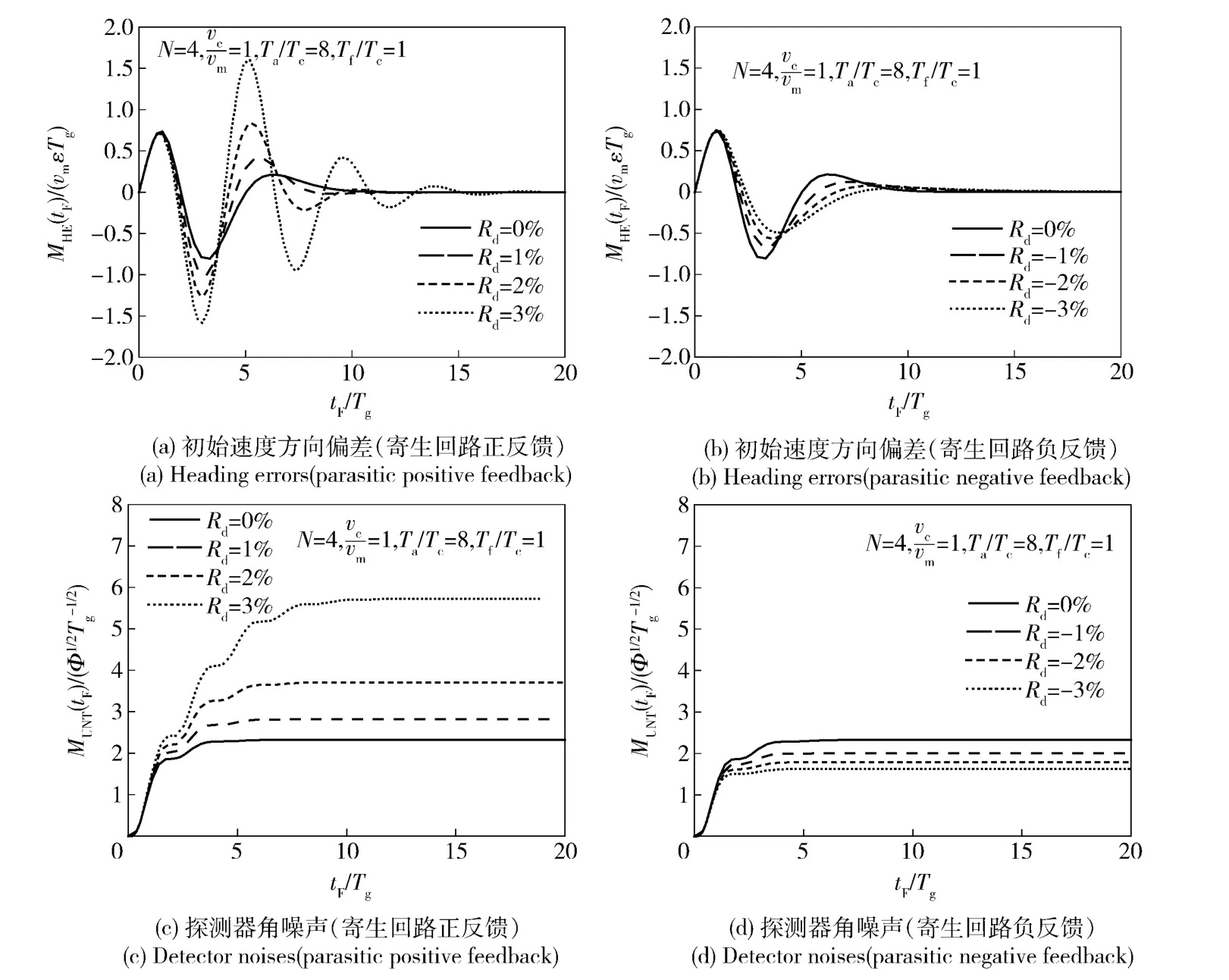
图12 隔离度对制导系统无脱靶量影响Fig.12 Effect of parasitic loop on miss distance

此处选取2 阶制导滤波器模型，分析可知制导滤波器时间常数将影响滤波的精度和响应时间，进而影响脱靶量收敛情况。仿真条件选取N = 4，vc/vm=1.0，Rd= ±3%，Tα/Tg=4，考察不同的滤波器无量纲时间常数Tf/Tc的变化对脱靶量的影响，仿真结果如图13所示。Tα/Tg不变，隔离度水平保持不变，初始速度偏差干扰作用下，脱靶量收敛情况受Tf/Tc影响较小。可见工程应用中，当Tα/Tg选定后，在初始速度偏差干扰下，脱靶量收敛情况已经固定。令Tα/Tg和隔离度水平保持不变，在探测器角噪声干扰作用下，随着Tf/Tc的增大，脱靶量将减小，即在保持制导时间常数不变情况下，适当降低制导滤波器的带宽，将有利于减小探测器噪声引起的脱靶量。综上所述，制导时间常数选定后，改变Tf/Tc对初始速度偏差引起的脱靶量无影响，只会影响探测器角噪声引起的脱靶量。实际工程应用中，可适当增加Tf/Tc，减小探测器角噪声引起的脱靶量。

取tF=10Tg，研究在不同制导系统内部动力学Tf/Tc情况下，脱靶量随隔离度的变化趋势，仿真结果如图14所示。

由图14可知，脱靶量对隔离度正反馈比负反馈更加敏感。适当增大Tf/Tc可延缓负反馈情况下脱靶量发散，对正反馈情况下脱靶量几乎没有影响。这与增大Tf/Tc可增大隔离度寄生回路负反馈稳定域相一致。

4 结论

本文分析了捷联成像导引头隔离度寄生回路产生原因，建立了刻度尺系数误差、导引头相位滞后引起的隔离度寄生回路模型。分析了两种不同机理产生的隔离度寄生回路模型的稳定性，研究了制导控制系统内部动力学特性对隔离度寄生回路稳定域和比例导引制导系统脱靶量的影响，得出以下结论:

1)刻度尺系数误差和导引头相位存在滞后导致隔离度寄生回路的存在，由于误差的不确定性，隔离度寄生回路可能是正反馈，也可能是负反馈。

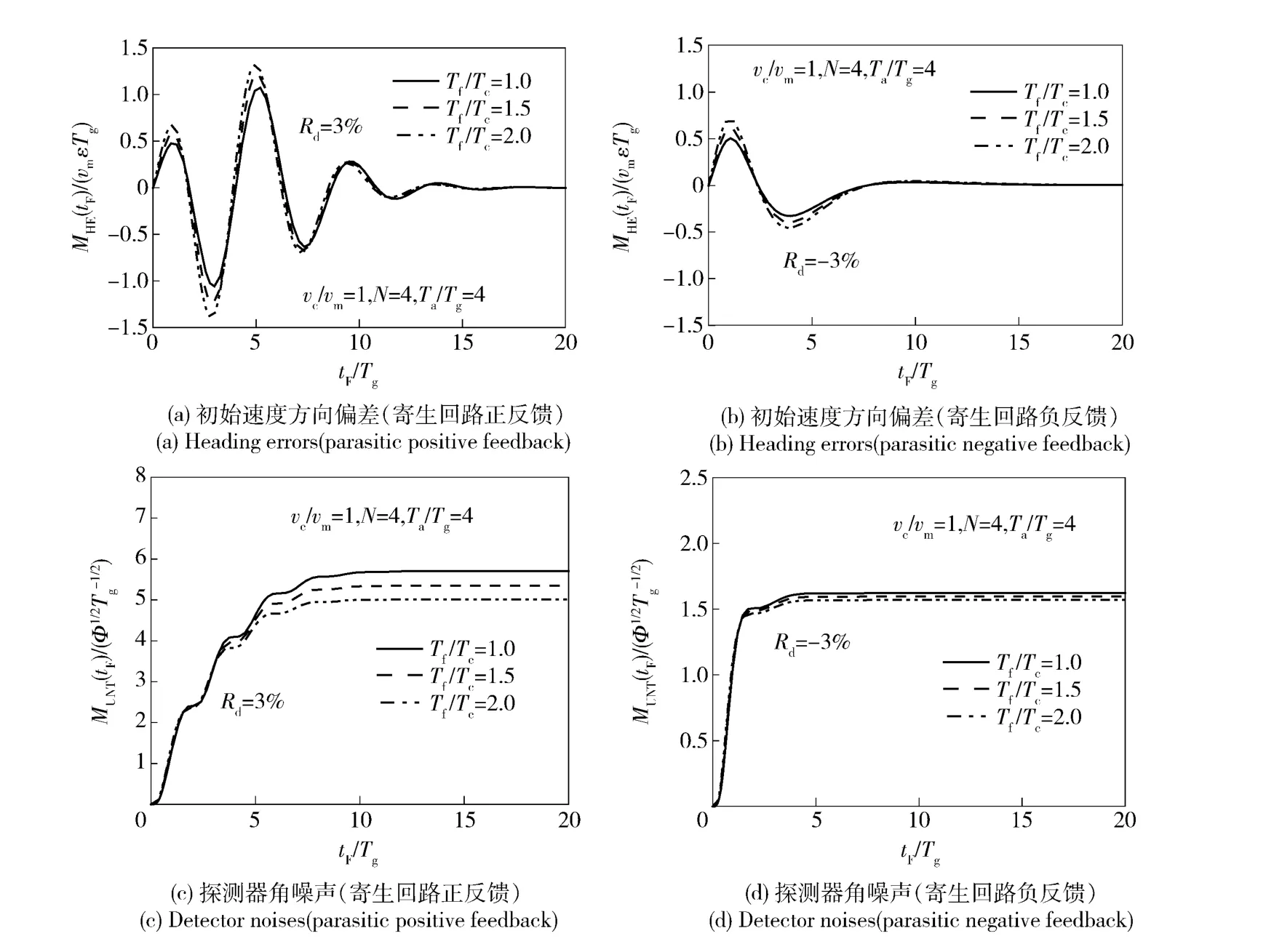
图13 制导系统内部动力学对脱靶量影响Fig.13 Effect of internal dynamics of guidance system on miss distance

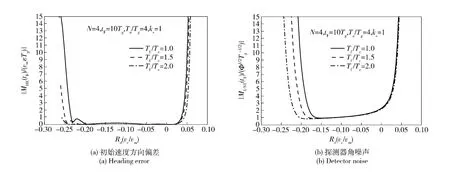
图14 无量纲脱靶量随Rd(vc/vm)变化曲线Fig.14 Dimensionless miss distance versus Rd(vc/vm)

2)刻度尺误差引起隔离度寄生回路的稳定性在正反馈时稳定域较小，负反馈时稳定域较大。制导剩余时间影响正反馈稳定域，制导滤波器和自动驾驶仪的动力学分配影响负反馈稳定域。导引头相位滞后引起的隔离度寄生回路的稳定性不受制导系统内部动力学的影响，只与导引头的延时程度有关，导引头延时越大，越容易导致隔离度寄生回路失稳。

3)隔离度寄生回路对制导系统的影响随着隔离度水平的增大而加大。在相同隔离度水平和制导时间常数保持不变情况下，适当增大制导滤波器时间常数可适当增大负反馈下的稳定域，且有利于降低探测器噪声引起的脱靶量，而对初始速度偏差扰动引起的脱靶量收敛无明显影响。适当增大制导滤波器时间常数，同时可延缓负反馈情况下脱靶量发散。

鉴于捷联成像导引头工作中刻度尺误差和导引头相位滞后同时存在，实际应用需要从导弹总体的角度综合考量捷联成像制导体制下的分系统指标分配和参数设计。

References)

［1］ 姚郁，章国江. 捷联成像制导系统的若干问题探讨［J］. 红外与激光工程，2006，35(1):1 -6.YAO Yu，ZHANG Guo-jiang. Discussion on strapdown imaging guidance system［J］. Infrared and Laser Engineering，2006，35(1):1 -6.(in Chinese)

［2］ Zarchan P. Tactical and strategic missile guidance［M］. Virginia:AIAA，2007:110 -116.

［3］ Nesline F W，Zarchan P. Radome induced miss distance in aerodynamically controlled homing missile［C］∥Proceedings of AIAA Guidance and Control Conference. New York:AIAA，1984.

［4］ 杜运理，夏群利，祁载康. 导引头隔离度相位滞后对寄生回路稳定性影响研究［J］. 兵工学报，2011，32(1):28 -32.DU Yun-li，XIA Qun-li，QI Zai-kang. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop［J］. Acta Armamentarii，2011，32(1):28 -32. (in Chinese)

［5］ Mehra R K，Ehrich R D. Air-to-air missile guidance for strapdown seekers［C］∥The 23rd IEEE Conference on Decision and Control.Las Vegas:IEEE，1984.

［6］ Willman W W. Effects of strapdown seeker scale-factor uncertainty on optimal guidance［J］. Journal of Guidance，Control，and Dynamics，1988，11(3):199 -206.

［7］ Jang S，Ryoo C，Choi K，et al. Guidance algorithms for tactical missiles with strapdown seeker［C］∥SICE Annual Conference.Tokyo:IEEE，2008.

［8］ 徐平，王伟，林德福. 导引头隔离度对末制导炮弹制导控制的影响［J］. 弹道学报，2012，24(1):17 -21.XU Ping，WANG Wei，LIN De-fu. Effect of seeker isolation on guidance and control of terminal guided projectile［J］. Journal of Ballistics，2012，24(1):17 -21. (in Chinese)

［9］ 李富贵，夏群利，崔晓曦，等. 导引头隔离度寄生回路对视线角速度提取的影响［J］. 宇航学报，2013，34(8):1072 -1077.LI Fu-gui，XIA Qun-li，CUI Xiao-xi，et al. Effect of seeker disturbance rejection rate parasitic loop on line of sight rate extraction［J］. Journal of Astronautics，2013，34(8):1072 -1077. (in Chinese)

［10］ Dorf R C. Modern control systems［M］. Boston:Addison-Wesley Longman Publishing Co Inc，1995.

［11］ 王嘉鑫，林德福，祁载康，等. 全捷联相控阵雷达导引头隔离度寄生回路研究［J］. 北京理工大学学报，2013，33(11):1124 -1129.WANG Jia-xin，LIN De-fu，QI Zai-kang，et al. Study on disturbance rejection rate parasitical loop of strapdown phased array radar seeker［J］. Transactions of Beijing Institute of Technology，2013，33(11):1124 -1129. (in Chinese)

［12］ 宋韬，林德福，王江. 平台导引头隔离度对导弹制导系统影响［J］. 哈尔滨工程大学学报，2013(10):1234 -1241.SONG Tao，LIN De-fu，WANG Jiang. Influence of seeker disturbance rejection rate on missile guidance system［J］. Journal of Harbin Engineering University，2013(10):1234 - 1241. (in Chinese)