火炮身管阳线损伤机理分析
曾志银,马明迪,宁变芳,高小科
(西北机电工程研究所,陕西咸阳712099)
0 引言
某大口径火炮A 号装药实弹射击时身管阳线出现损伤,损伤发生在膛线起始点前35 ~45 mm 范围内,该范围处于弹丸挤进过程的膛线起始段,阳线损伤呈45°八字型双侧棱边脱落,断口规整,无明显韧性撕裂痕迹,损伤形貌如图1所示。

图1 阳线损伤形貌图Fig.1 Shape appearance of rifling land damage
对于膛线损伤及弹丸挤进过程,目前国内开展了大量的仿真与试验测试研究,主要集中于卡膛过程、挤进阻力的仿真与计算,重点关注弹丸及弹带的动力响应,一般将模型简化为轴对称模型,或者将身管假定为刚体等。文献[1]在引入了弹带各截面上同一时刻应力相等的近似假设下,建立了弹丸挤进过程的轴对称模型。文献[2]建立了弹丸挤进枪管的有限元模型,假定身管为刚体,研究了铅芯弹丸的挤进过程。文献[3]利用动态光弹法研究了膛线脱落的机理,在均布冲击载荷的作用下,承载膛线两侧根部的应力极值点出现起裂,从而形成膛线脱落。其研究与实际膛线受力状态不同,不能反映阳线棱边应力集中。文献[4]在分析了高冲击下弹带材料应变特性的基础上,建立了2 阶系统模拟弹丸挤进过程的计算方法。文献[5 -6]基于弹塑性有限元接触理论,引入弹带材料的初始损伤及累计损伤模型,在弹丸与身管理想同轴及均匀摩擦前提下,建立了弹丸挤进的非线性有限元模型,分析了坡膛结构变化对弹丸挤进过程的影响。文献[7]对火炮坡膛涂油条件下弹丸挤进润滑状态进行了分析,建立了涂油挤进摩擦和油膜厚度的模型,以130 mm 火炮为研究对象得到弹丸挤进过程摩擦系数的表达式。文献[8]研究了铜合金在不同工况下的摩擦系数,通过试验得到低载荷下的摩擦系数以及大部分弹带嵌入膛线时摩擦系数。文献[9]通过试验测出了弹底压力,并利用“接触法”和“测压法”同时测出了挤进压力。文献[10]对射击过程中弹丸与身管的作用从理论和试验方面进行了综述。文献[11]对射击过程中弹丸挤进时弹带应力应变进行了研究。文献[12]论述了由于炮膛除油不净造成身管阳线剥落故障,并对膛内油污造成的阳线损伤原因进行了分析。
国外开展了大量有关弹丸膛内运动规律的研究,针对弹丸在膛内的运动响应及身管的振动特性,仅限于弹丸膛内响应规律研究,忽略了弹丸挤进过程身管动态响应特性研究[13]。
本文在前人研究的基础上,基于弹塑性有限元接触理论,建立了某大口径火炮的弹丸身管耦合系统有限元动力学模型。考虑了弹丸装填不到位、初始装填角、弹炮间隙、弹带强制量、非均匀摩擦、动态载荷作用下炮钢材料动态力学行为等多因素对身管动力响应的影响,加深了对弹丸挤进过程身管阳线动力响应规律的认识,初步揭示了某大口径火炮身管阳线损伤机理。
1 计算模型
1.1 身管及弹丸网格处理
本文以某大口径火炮弹丸身管耦合系统为研究对象,计算模型包括身管、弹带和弹体。身管模型中除膛线起始段局部单元采用棱柱单元过渡外,其他部位均采用Solid164 六面体单元,图2为身管有限元网格局部图。

图2 身管有限元网格局部图Fig.2 Partial grid of finite element of barrel
由于某火炮为线膛炮,膛线存在一定缠度,因此弹带被阳线刻出的沟槽有一定角度。为了减小计算中的网格畸变,在弹带网格划分时使其保持与膛线初始缠角相同的角度,图3为弹丸有限元网格。
1.2 材料模型
身管为炮钢材料PCrNi3MoVA,采用双线性模型。弹带为H96 黄铜,采用Johnson-Cook 模型。Johnson-Cook 模型适合描述大部分金属材料[14]。大变形、高应变率和高温条件下的应力应变关系,表达式为
图3 弹体有限元网格图Fig.3 Finite element grid of projectile
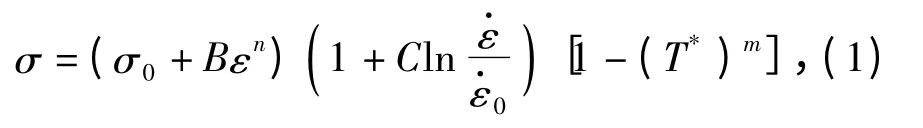
式中:σ0、B、C、n、m 为材料常数,σ0=275 MPa,B =505 MPa,C=0.009,n =0.42,m =1.68;ε 为等效塑性应变;为等效塑性应变率;为参考应变率为相对温度,Tr为室温,Tm为材料熔点温度。
1.3 接触算法
本文计算模型中共有3 个接触对,即弹带与身管内表面、弹体与身管内表面、弹带与弹体。
1)弹带与身管内表面的接触-碰撞及弹体与身管内表面的接触-碰撞模型:以弹带与身管内表面接触-碰撞模型为例,将弹带结点定义为从结点,将身管内表面定义为主表面。采用罚函数法,计算中每一时间步检查弹带从结点是否穿透主表面,没有穿透不做任何处理,否则在该从结点与被穿透的主表面间引入一个大小与穿透量及主表面单元刚度呈正比的接触力。这种处理方法相当于在从结点和被穿透的主表面之间设置一个法向弹簧,以限制从结点对主表面的穿透。
2)弹带与弹体的固连接触模型:将弹带结点定义为从结点,将与弹带相接触的界面上的弹体单元表面定义为主表面,仅约束弹带从结点的平动自由度。如果弹带从结点与对应的主表面存在微小的距离,则采用正交投影的方法将从结点移动到主表面上。在每一个时间步中首先将每一个从结点的质量和结点力分配到该从结点接触点的主片各结点上,然后计算各主结点的加速度。从节点的加速度可以由包含其接触点的主片各结点加速度插值得到[15]。
1.4 计算工况
针对某大口径火炮出现膛线损伤时的射击条件,模型采用A 号装药,根据弹底压力-时间曲线,施加弹底压力,以模拟火药气体对弹丸的冲击作用。计算分别考虑以下8 种工况:
1)身管和弹丸结构均采用名义尺寸,弹轴与身管轴线重合,初始装填角为0°;
2)身管和弹丸结构均采用名义尺寸,弹丸取所允许的最大装填角0.006 7°;
3)身管阳线采用公差上限,弹丸定心部采用公差下限,此工况弹炮间隙最大;
4)身管和弹丸采用工况2 模型,弹丸前定心部未进入直膛段,取该状态下弹丸极限装填角度,弹丸初始装填速度取5 m/s,弹尖向上倾斜,模拟弹丸装填及卡膛过程;
5)身管和弹丸采用工况3 模型,弹丸前定心部未进入直膛段,取该状态下弹丸极限装填角度,弹丸初始装填速度取5 m/s,弹尖向上倾斜,模拟弹丸装填及卡膛过程;
6)选取第2 种工况计算模型,增大摩擦系数,模拟不同摩擦阻力对身管响应的影响;
7)计算模型同工况6,身管内膛不同区域与弹丸之间的摩擦系数不同,模拟非均匀摩擦对身管响应的影响;
8)计算模型同工况7,改变弹丸的初始装填位置,模拟装填不到位对身管响应的影响,取装填不到位最恶劣情况(弹丸距离合膛位置90 mm)。
2 数值模拟结果分析
2.1 膛线起始至直膛开始段应力
图4为工况6 不同时刻膛线起始至直膛开始段应力分布图。由图4可以看出,随着弹丸的挤入,在膛线起始段形成一系列的等效应力带,阳线部分应力远大于阴线。1.4 ms 左右,前弹带开始刻槽,与弹带接触的阳线出现明显应力集中,应力集中主要出现在阳线双侧棱边上,最大等效应力约1 000 MPa. 随着弹丸继续挤进,膛线起始段应力逐渐增大,3 ms 左右最大等效应力约1 400 MPa,阳线导转侧应力高于非导转侧,相对阳线导转侧和非导转侧,阳线上表面应力要小。3.5 ms 左右弹丸挤进基本完成,阳线应力下降并趋于稳定。膛线起始至直膛开始段阳线棱边应力集中严重,弹带变形阻力和摩擦力均达到峰值,是膛线磨损严重和损伤的多发位置。
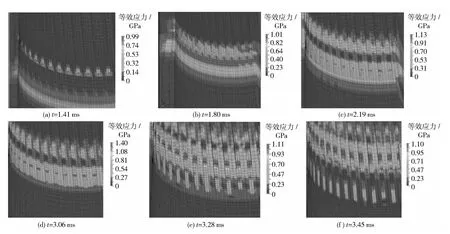
图4 工况6 不同时刻坡膛等效应力分布图Fig.4 Equivalent stress distributions at 6 different times
为了进一步分析弹丸挤进过程中膛线起始段的应力变化情况,在阳线导转侧、非导转侧及表面沿轴线方向各取5 个单元,选取单元位置如图5所示。1 号单元位于膛线起始点;2 号单元位于1 号和3 号单元之间;3 号单元位于膛线起始点前29.3 mm;4 号单元位于坡膛结束位置;5 号单元位于直膛段。图6、图7、图8分别为阳线导转侧、非导转侧及上表面等效应力随时间变化曲线(图中仅取1、3、5三点)。
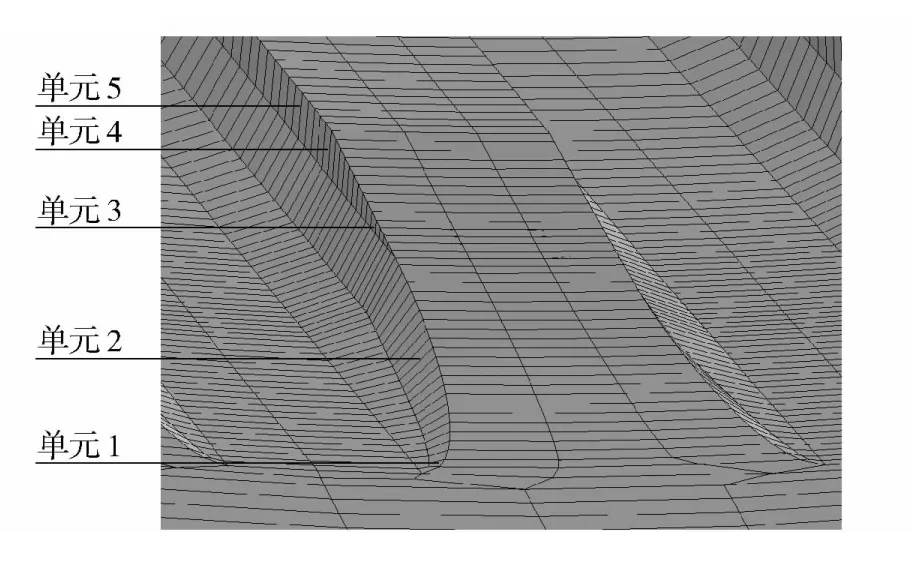
图5 阳线表面选取单元分布图Fig.5 Distribution of the selected element on the surface of rifling land
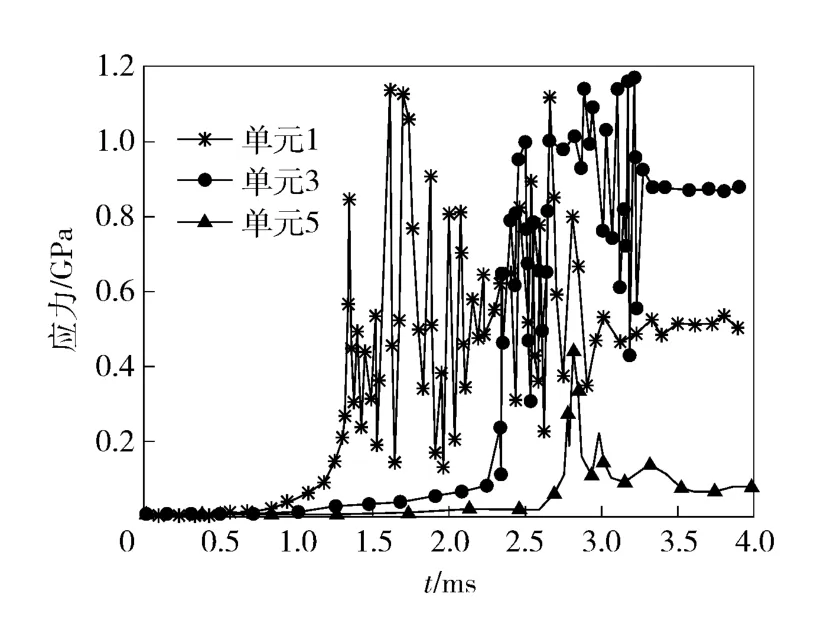
图6 工况6 阳线导转侧等效应力Fig.6 Equivalent stress in inversion side of rifling land of Condition 6
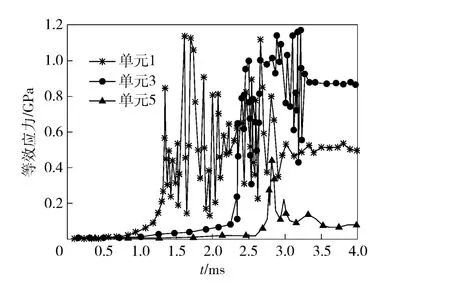
图7 工况6 阳线非导转侧等效应力Fig.7 Equivalent stress in non-inversion side of rifling land of Condition 6
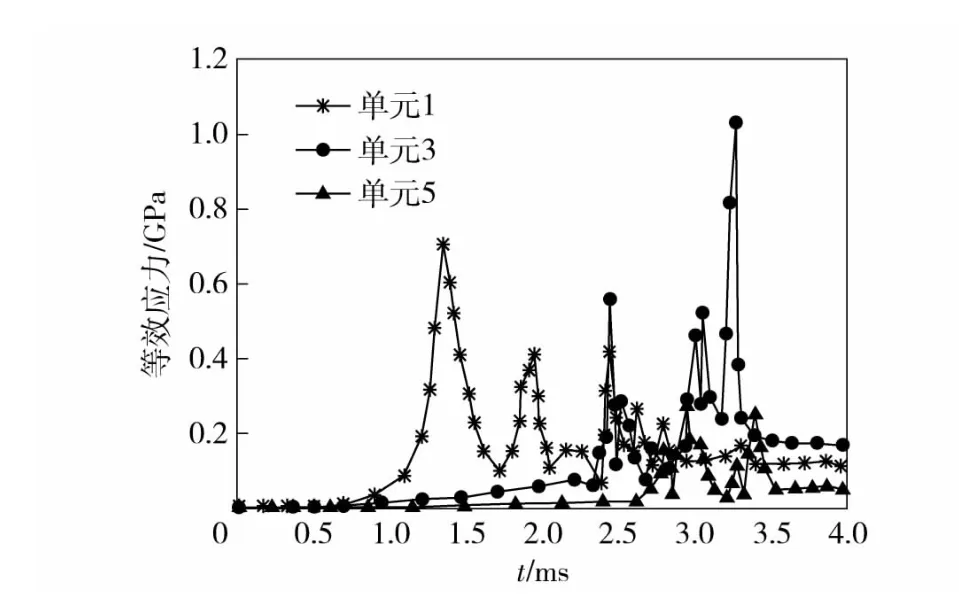
图8 工况6 阳线上表面等效应力Fig.8 Equivalent stress in upper surface of rifling land of Condition 6
2.2 装填不到位与到位响应对比
工况8 计算结果表明,由于弹丸装填不到位,弹丸在到达设计合膛位置之前就开始加速运动,到达合膛位置时其速度已经达到约80 m/s,造成弹带与身管以及弹体与身管之间产生较大撞击力。装填到位与装填不到位弹带、弹体与身管撞击力对比曲线如图9、图10所示。由图9和图10对比结果看,与装填到位相比,弹丸装填不到位时弹带与身管之间撞击力是其约3.7 倍,弹体与身管之间撞击力是其约1.5 倍。
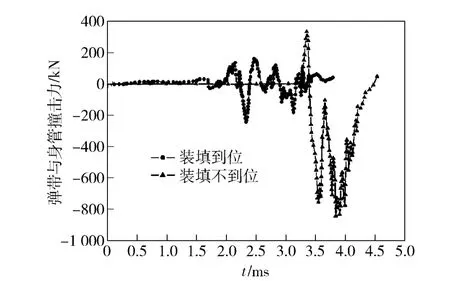
图9 不同装填状态弹带与身管之间的撞击力Fig.9 Theimpact force between barrel and ammunition belt under different loading states
3 损伤机理综合分析及其验证
3.1 损伤机理综合分析
在8 种计算工况中,其中工况1、2、3、6、7 为主要模拟弹丸挤进过程,工况7 模拟非均匀摩擦对身管响应的影响;4、5 两种工况主要模拟不同装填速度和初始装填角下弹丸卡膛过程;工况8 主要模拟弹丸装填不到位对身管阳线动力响应的影响。

图10 不同装填状态弹丸与身管之间的撞击力Fig.10 The impact force between barrel and ammunition belt under different loading states
前3 种计算工况相比,工况2 弹丸挤进过程中身管阳线应力水平较高,弹管间隙越小,弹丸初始装填角度摆正过程中身管阳线应力越大。其主要是由于弹丸与身管间隙变小后弹带强制量增加,致使弹丸挤进过程中阳线应力提高,同时,弹丸初始装填角加剧了膛线起始点向前至48 mm 这一段阳线应力的变化梯度。挤进过程中阳线高应力区域一定出现在膛线起始点至直膛开始这一段,其原因:一是因为弹带强制量从膛线起始点至直膛开始逐渐从小到最大,随着挤进过程的进行,弹带变形逐渐增大至直膛开始并被阳线完全刻槽,这一过程对应阳线应力也同样逐渐增至最大;二是膛线起始点至直膛开始这一段,由于从坡膛过渡到直膛,阳线与阴线交界过渡圆角造成阳线结构特征发生突变(见图11),弹丸挤进过程中在这一段阳线棱边产生明显应力集中。
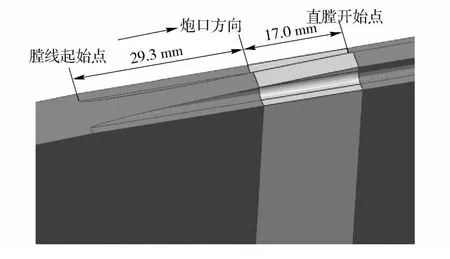
图11 阳线高应力对应位置示意图Fig.11 Schematic diagram of corresponding location of high stress on rifling land
与工况2 相比,工况6 摩擦系数增大后使弹丸运动阻力增加,导致身管阳线等效应力普遍提高,弹丸挤进过程中阳线整体应力水平较其他工况明显增大。阳线导转侧局部最大等效应力达到了1 400 MPa左右。最大等效应力出现在阳线局部棱边上,沿身管轴向最大等效应力出现位置大约在膛线起始点前28 ~48 mm 之间,与实际阳线损伤位置基本一致,阳线高应力对应几何区域如图11所示。
某大口径火炮A 号装药内弹道计算弹丸膛内运动时间为19.69 ms,最大膛压时间约8.2 ms,试验测试身管外表面最大应力出现时刻约为8.3 ms. 而弹丸挤进在阳线产生最大应力的时间约为3 ms,即弹丸挤进在身管中产生的最大应力要早于膛压作用出现的最大应力时刻,表明身管阳线损伤发生在弹丸挤进过程。虽然弹丸挤进过程在阳线局部产生较高的应力,但高应力区域仅限于身管壁厚局部范围,即沿径向小于5 mm.
从图1实弹射击阳线损伤形貌的观测与分析看出,膛线起始点前35 ~45 mm 范围内,部分阳线双侧棱边呈大约45°八字形剥落,且损伤断裂形状规整,无明显韧性撕裂痕迹。身管材料动力学行为研究表明,身管材料PCrNi3MoVA 随载荷作用速率的增加(应变率增加),其断裂韧性会随着下降,而屈服极限提高,如表1和表2所示。一方面由于阳线单元在弹丸挤进过程中沿轴向受阳线长度方向约束,沿径向受身管壁厚约束,阳线局部单元受到非等值六面压缩后(见图12)难以像单向压缩时的充分自由变形;另一方面由于弹丸装填不到位,弹带与身管之间撞击力及撞击速度的陡增,致使身管的加载速率提高而身管材料的断裂韧性下降,加剧了身管阳线局部发生由韧到脆的断裂转变,从而导致在阳线局部双侧棱边形成整齐的断裂形貌。单元应变率曲线如图13所示。

表1 PCrNi3MoVA 材料的静、动态断裂韧性Tab.1 The static and dynamic fracture toughness of PCrNi3MoVA
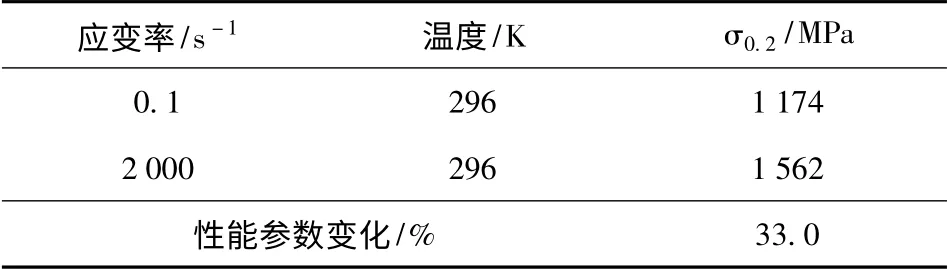
表2 PCrNi3MoVA 材料不同应变率下的性能参数Tab.2 The performance parameters of PCrNi3MoVA at different strain rates
3.2 损伤机理验证
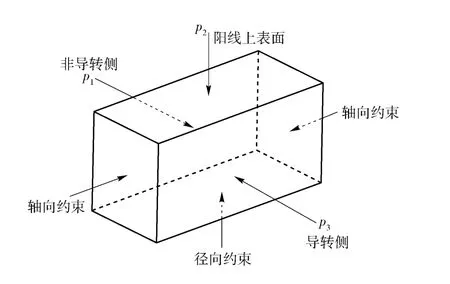
图12 阳线单元受力示意图Fig.12 Schematic diagram of force of rifling land element
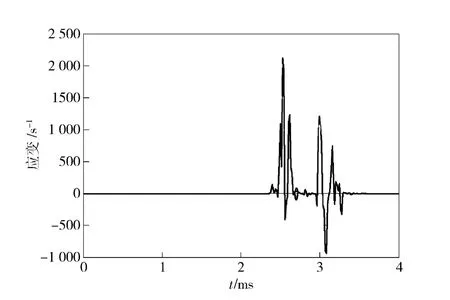
图13 阳线单元应变率曲线Fig.13 The strain ratecurve of element of rifling land
针对某火炮阳线损伤现象,在理论分析的基础上,进一步开展了损伤机理验证试验。其中试验进行了损伤部位对应外表面应力测试、膛压测试、初始装填角测试、内膛存在异物及油污情况下试验、弹丸装填不到位试验等多因素对身管响应的影响。试验时的装药、射角、弹药批次与出现阳线损伤时条件相同。在多因素的大量试验中,唯有弹丸装填不到位时身管复现了阳线损伤现象,复现的阳线损伤如图14所示,与以前出现的阳线损伤形貌、位置等相同。弹丸装填不到位实弹射击试验验证了阳线损伤机理的理论分析,确认了阳线损伤故障原因。

图14 阳线损伤复现图Fig.14 The recurrence of rifling land damage
4 结论
1)某大口径火炮膛线起始点至直膛开始段的结构特征及发射过程的弹丸挤进,必然在此段阳线产生最大应力及阳线棱边应力集中。该火炮膛线结构、弹带强制量,使得此处阳线应力已处于较高水平,但考虑到身管材料屈服极限随应变率的提高而提高,正常情况下不会造成阳线损伤。
2)弹丸运动摩擦阻力增加,将致使膛线起始点到直膛开始段阳线应力普遍提高,同时由于弹丸初始装填角的存在,进一步增加了这一段阳线动态应力的变化梯度。弹丸挤进过程造成阳线高应力区沿身管轴向集中在膛线起始点前大约28 ~48 mm 位置,与实际阳线损伤位置基本一致。
3)身管外表面应力试验及弹丸挤进数值模拟结果表明,某大口径火炮身管阳线损伤发生在弹丸挤进过程。弹带强制量是产生阳线压缩应力的主要因素,但弹丸挤进过程在身管产生的高应力区仅限于身管内壁径向很小范围。
4)非正常装填,即弹丸装填不到位时(距离设计合膛位置90 mm),弹丸到达设计合膛位置其速度已经达到约80 m/s,弹带与身管撞击力提高到约3.7 倍,弹丸定心部与身管撞击力提高到约1.5 倍。在膛线起始段已经存在高应力及阳线局部单元不能充分自由变形的基础上,加之弹丸装填不到位使加载率增加造成的身管材料断裂韧性降低因素,加剧了阳线局部发生由韧性到脆性的断裂转变,最终导致阳线双侧棱边形成无韧性撕裂痕迹的整齐断裂形貌。实弹射击试验验证了阳线损伤机理的理论分析。
References)
[1] 何勇. 弹丸挤进阻力的一维模型及计算[J]. 弹道学报,1994,22(4):24 -28.HE Yong. An one-dimensional almodel for the projectile engraving process and its calculation[J]. Journal of Ballistics,1994,22(4):24 -28.(in Chinese)
[2] 樊黎霞,何湘玥. 弹丸挤进过程的有限元模拟与分析[J]. 兵工学报,2011,32(8):963 -969.FAN Li-xia,HE Xiang-yue. Finite element simulation and engraving process analysis of projectile entering into barrel[J]. Acta Armamentarii,2011,32(8):963 -969.(in Chinese)
[3] 苏先基,赵泽全. 用动态光弹法研究炮身膛线的脱落问题[J]. 实验力学,1988,3(1):14 -23.SU Xian-ji,ZHAO Ze-quan. Dynamic photoelastic study of barrel rifle peeling off[J]. Journal of Experimental Mechanics,1988,3(1):14 -23.(in Chinese)
[4] 金志明,曾思敏. 弹丸挤进过程的计算与研究[J]. 兵工学报,1991,12(1):7 -13.JIN Zhi-ming,ZENG Si-min. A study on the calculation of the engraving process on projectiles[J]. Acta Armamentarii,1991,12(1):7 -13.(in Chinese)
[5] 孙河洋,马吉胜,张高明,等. 弹带挤进过程动力学仿真[J].四川兵工学报,2008,29(5):46 -49.SUN He-yang,MA Ji-sheng,ZHANG Gao-ming. The dynamical simulation of engraving process analysis of ammunition belt[J]. Journal of Sichuan Ordnance,2008,29(5):46-49.(in Chinese)
[6] 孙河洋,马吉胜,李伟,等. 坡膛结构变化对弹带挤进过程影响的研究[J]. 振动与冲击,2011,30(3):30 -33.SUN He-yang,MA Ji-sheng,LI Wei,et al. Influence of different bore structures on engraving process on projectile[J]. Journal of Vibration and Shock,2011,30(3):30 -33.(in Chinese)
[7] 彭志国,周彦煌,何锁. 火炮坡膛涂油挤进摩擦模型与分析[J]. 弹道学报,2007,19(3):68 -72.PENG Zhi-guo,ZHOU Yan-huang,HE Suo. Model and analysis of bands entrance andfriction with oil on gun cone[J]. Journal of Ballistics,2007,19(3):68 -72. (in Chinese)
[8] 江敬媛. 在弹带嵌入膛线和弹丸起始行程中弹带材料的摩擦[J]. 现代兵器,1982(1):37 -40.JIANG Jing-yuan. The friction of ammunition belt material in the beginning of engraving process on projectiles[J]. Modern Weaponry,1982(1):37 -40. (in Chinese)
[9] 曾思敏,童伟民,焦化南. 弹丸挤进过程的测试与研究[J]. 弹道学报,1991,10(4):1 -7.ZENG Si-min,TONG Wei-min,JIAO Hua-nan.Measurement and study of the engraving process of projectile[J]. Journal of Ballistics,1991,10(4):1 -7.(in Chinese)
[10] 吴斌,郑靖. 枪炮射击过程中弹丸与身管相互作用及其影响[J]. 四川兵工学报,2011,32(5):20 -23.WU Bin,ZHENG Jing. Projectile interaction with gun barrel and its effect during firing process[J]. Journal of Sichuan Ordnance,2011,32(5):20 -23.(in Chinese)
[11] 彭涛,王学军,黄善文. 基于ANSYS 的弹带挤进变形及应力分析[J]. 舰船电子工程,2009,185(11):156 -158.PENG Tao,WANG Xue-jun,HUANG Shan-wen. Analysis on material deformation and stress in the process of driving band engraving based on ANSYS[J]. Ship Electronic Engineering,2009,185(11):156 -158. (in Chinese)
[12] 杨英梅. 炮膛除油不可轻视[J]. 兵器知识,2012(3):48-49.YANG Ying-mei. Oil removal of bore cannot be contempt[J].Ordnance Knowledge,2012(3):48 -49.(in Chinese)
[13] Projectile motion in a flexible gun tube,ADA149022[R]. Maryland:US Army Ballistic Research Laboratory,Aberdeen Proving Ground,1984.
[14] Meyers M A. 材料的动力学行为[M]. 张庆明,刘彦,黄风雷,等,译. 北京:国防工业出版社,2006:226 -228.Meyers M A. Dynamic behavior of materials[M]. ZHANG Qingming,LIU Yan,HUANG Feng-lei,et al. translated. Beijing:National Defense Industry Press,2006:226-228.(in Chinese)
[15] 张雄,王天舒. 计算动力学[M]. 北京:清华大学出版社,2007.ZHANG Xiong,WANG Tian-shu. Computional dynamics[M].Beijing:Tsinghua University Press,2007.(in Chinese)

