基于改进蚁群算法的协作学习分组研究

胡慧，何聚厚，2

1.陕西师范大学计算机科学学院，西安710062

2.陕西师范大学现代教学技术教育部重点实验室，西安710062

1 引言

协作学习中根据学习者的特征进行有效分组，对于提高学习者的学习效率具有重要影响[1-2]。传统的分组方式有随机选择法和穷举法[3]。随机选择法并未考虑学习者的特征差异与具体的活动类型，易造成整体上的学习效率不高[4]。穷举法在学习者个体数比较多且考虑学习者特征时，无法在短时间内进行有效分组[5]。为此，Graf和Bekele于2006年，针对组内异质分组模型通过蚁群算法来解决分组问题[6]；Hwanget等于2008年提出基于遗传算法的分组模型[7]。这两种方法虽然考虑了学习者的多个特征，但都没有考虑活动类型及特征的权值对分组的影响。Lin等于2010年提出基于改进粒子群算法来解决分组问题[8]，该算法仅考虑了学生的理解水平和兴趣爱好两个特征。

考虑学习者多个特征及根据活动类型的不同为不同特征赋予不同的权值，则协作学习中的分组问题变为多目标优化问题。本文在蚁群算法中将学习者特征相似度值作为启发信息，并在初期融入判断-回退机制构造分组，增加分组的多样性，避免算法出现早熟收敛现象；在中后期对信息启发因子和期望因子进行动态调整，避免寻优出现停滞现象。

2 分组问题描述

在协作学习中，基于学习者特征的量化值，将N个学习者分为K组，其目标是使每组学习者在协作学习中学习效率最高。

定义1 学习者特征集合A定义为：

其中，La（Learning ability）学习能力，In（Interests）为兴趣爱好，U l（Understanding level）为理解水平。对于某一学习者，通过测试过程f可以获得对应特征的量化值。

定义2学习者集合S定义为：

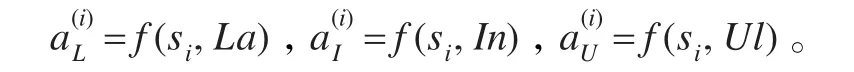
引入特征权值控制不同特征在分组过程中的贡献。

定义3 特征权值集合定义为：

且wL+wI+wU=1。wL、wI和wU分别是La、In和U l对应的权值。

学习者之间通过特征相似度进行量化比较。

定义4 学习者si和sj之间的特征相似度通过下式计算：

若sim(si，sj)越小，则si和sj之间的特征相似度越高。

将N个学习者分为K组，则所有的分组方式构成分组空间。

定义5 分组空间为：

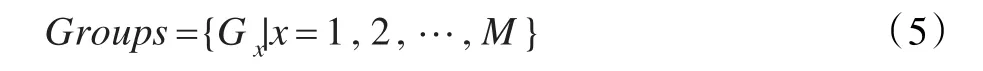
其中，M为分组方式的个数。对于每一种分组方式Gx，有：

其中，K为分组个数。对于某一分组方式Gx，若学习者si被分到了小组，为了叙述方便学习者记为，则。假定某一学习者只能被分到一个小组，且所有的学习者都会被分到某一分组，因此对于和，有：

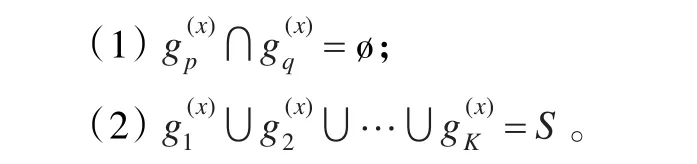
引入特征平均值作为度量分组准确性的参考值。

定义6 对于分组方式Gx，其特征平均值集合Cx定义为：

定义7 协作学习中的分组问题定义为：

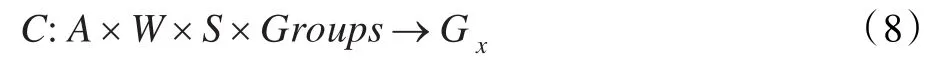
即分组过程为基于学习者特征集合A，特征权值集合W和学习者集合S在分组空间Groups中确定最佳分组方式Gx的过程。为此，Gx需满足如下条件。

目标函数：

约束条件：

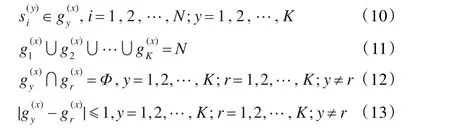
在目标函数表达式中，F值表示分组方式Gx中各小组均方差之和，该值越小，则说明在Gx中∈Gx的各组内均方差越小，即同一小组内学习者特征相似度越高。

约束条件（10）和（11）保证了N个学习者都会被分到某一小组中；约束条件（12）保证了每位学习者只能被分到某一个小组中；约束条件（13）限制了小组之间人数相差不超过一人。

故分组问题的求解即在满足上述约束条件的前提下，在分组空间Groups中找到使目标函数值F最小的分组方式Gx，使分组后学习者的学习效率最优。

3 EACO算法分组过程描述

算法首先初始化相关参数并根据定义4计算出N个学习者两两之间的相似度值。通过迭代选择最优分组的过程为：将R只蚂蚁按照判断-回退的机制从集合S中选择起始学习者，并按照转移概率公式选择下一个学习者，直到将N个学习者遍历完即形成R种分组方式，计算各组F值并获得当代最优分组方式。按照max-m in机制更新全局信息素，并计算相邻两代之间最优值的差值ΔF，如果小于某一阈值，则通过改变转移概率公式中的f1和f2的值动态调节启发因子和期望因子。如果迭代次数大于最大迭代次数阈值t_max，停止迭代并输出F值最小的分组方式Gbest。

算法步骤：

步骤1 初始化参数。

获取N个si∈S:{s1，s2，…，si，…，sN}，分别通过函数

将N个学习者个体的特征La、In、U l量化值变换到[0，1]；初始化相关参数：最大迭代次数t_max，蚂蚁数R，信息素初始化矩阵Matrix1N×N，信息素挥发概率ρ等。

步骤2 计算学习者特征相似度。

根据定义4分别计算个体si与其他学习者的相似度值sim(si，sj) ，并存储于矩阵Matrix2N×N中：

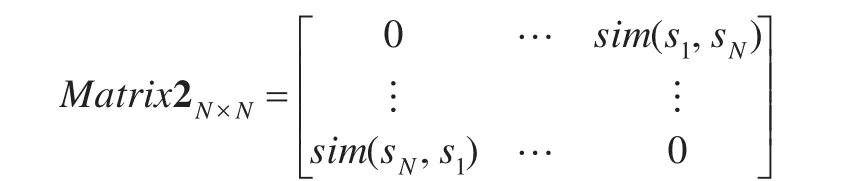
因Matrix2N×N具有对称性，故只需填充矩阵上三角的相似度值。

步骤3 选择起始学习者个体。

采用数组p记录每只蚂蚁起始学习者的编号。为避免蚂蚁个体寻优时对同一学习者重复选择，采用禁忌表tabuk记录已选学习者。伪代码如下：

for每只蚂蚁

{从集合S中任意选取学习者si作为起点；

if（si编号未在数组p中）

将si的编号存于起始数组p中；

p=[i]；

将si存于禁忌表tabuk中；

tabuk=[si]，以si为起点构造分组方式Gx；

else

从集合S中重新选取学习者sj；

跳转到if语句重新判断；

}

步骤4 根据转移概率公式选择路径。

在状态转移概率公式中添加了两个调节因子f1和f2，当相邻两代函数值F差值小于某一阈值q时，则通过f1和f2分别对启发因子α和期望因子β进行动态调节。转移概率公式如下：

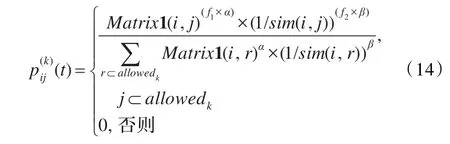
蚂蚁按照公式（14）选择与当前学习者si相似度最大的sj移动。在蚂蚁移动过程中，将对学习者sj分配小组号，其伪代码如下：

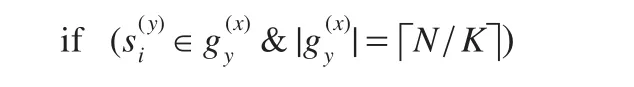
执行上述四步，直到每只蚂蚁将N个学习者遍历完，则∀si∈S都被分到某一小组g(x)y∈Gx中，形成分组空间Groups={Gx|x=1，2，…，R}。

步骤5 更新局部信息素。

对于∀Gx∈Groups，根据式（9）计算出F值，按照公式（15）更新局部信息素：

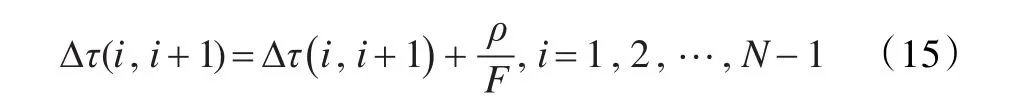
步骤6 比较∀Gx中F值的大小，获得此次迭代的最佳分组方式Gx。

步骤7 结合max-m in机制更新全局信息素。

按照公式（16）对全局信息素进行更新：

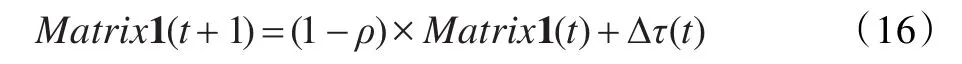
为避免某些路径可能长时间没有蚂蚁经过导致信息素为0，使算法陷入局部最优，本文对信息素的最大最小值进行了限制，在保留优秀解的同时增加分组方式的多样性。

步骤8 如果ΔF＜q，则调整f1'=f1+Δf1，f2'=f2+Δf2；否则，f1、f2保持不变。

步骤9 置t :=t+1，若t＜t_max，信息素增量归0，转步骤3；否则，算法结束，并输出F值最小的分组方式Gbest。

4 实验及结果分析

4.1 参数设置

实验采用M atlab7.0实现该算法。N∈[10，50]，小组人数为5人[9]，学习者特征La、In、U l的量化采用产生随机数的方法，再通过函数f将量化值转换到[0，1]区间；特征权重值为W={0.2，0.5，0.3}。EACO相关参数设置如表1所示。

信息素挥发概率：ρ=0.4；调节因子初值：f1=1，f2=1；增量值：Δf1=0.05，Δf2=-0.03；启发因子：α=2；期望因子：β=2；信息增量初值Δτ=0；R=2/3×N[10]。

4.2 EACO性能分析

为验证EACO算法分组的准确性，本文选取4.1节中的三组数据分别用穷举法（EM）、随机选择法（Ran-dom）、基本蚁群算法（ACO）做对比实验。

表1 实验参数表

当N=10时，EM算法（实线）、ACO算法（虚线）和EACO算法（点画线）的实验结果如图1所示。

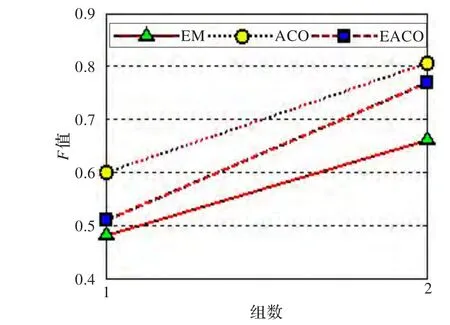
图1 和组内F值(N=10)

由图1可见，此时穷举法得到的最佳分组方式中各小组的F值最小，组内学习者的特征相似度最高。但该方法只能应用于少数学习者，具有很大的局限性。而EACO算法获得的最优分组方式中各小组的F值此时也极接近最优值。

当N=25和N=50时，Random算法（实线）、ACO算法（虚线）和EACO算法（点画线）的实验结果，分别如图2和图3所示。

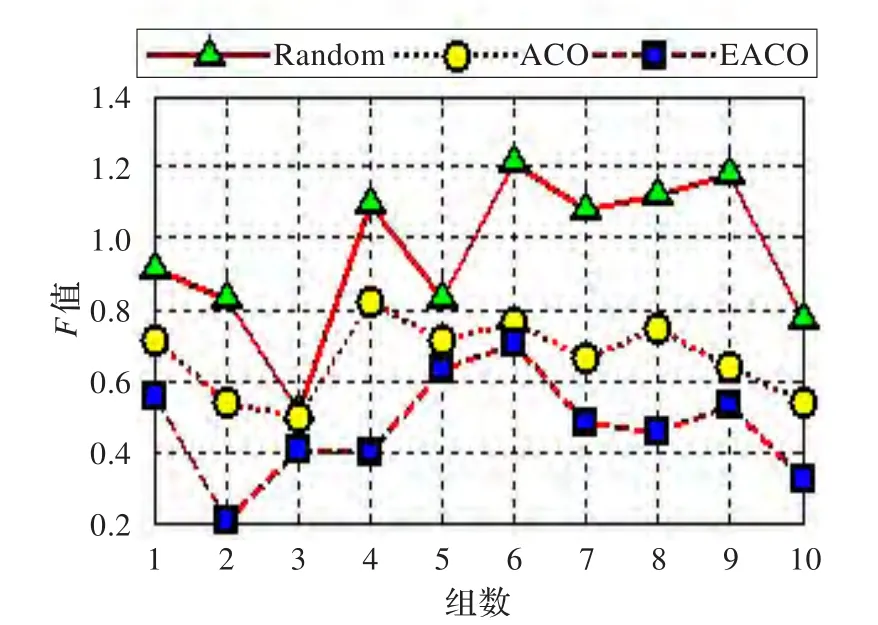
图3 ～组内F值(N=50)

学习者之间的有效交互是提高协作学习效率的基本条件之一[11-12]。基于学习者的学习能力、兴趣爱好和理解水平，采用EACO算法更准确地将特征最相似的个体分在同一小组，促进了学习者更充分地讨论、交流，不会导致个别学习者因对课题缺乏兴趣或者学习能力、理解水平太低而孤立[13]。此外，教育者可视各组学习者的兴趣爱好、学习能力和理解水平的不同，为各组学习者安排不同类型、不同难易程度的协作活动，这更加促进了学习者之间交互的积极性[8]。从教育心理学角度而言，学习者往往更倾向于与兴趣爱好相同的伙伴在一起学习[14]。因此在考虑学习者学习能力和理解水平的同时，结合其兴趣爱好也是令学习者更满意的分组方式。由图2和图3可见，EACO算法相对于传统算法能够获得使各小组F值更小的分组方式Gx，使小组内学习者的特征相似度更高，这有利于学习者之间更好的交流，提高学习效率。

为测试EACO算法的时间性能，对4.1节中的每组数据做10次测试，选取重复率最高的结果作为最终记录，并分别与EM算法、Random算法和ACO算法做比较。结果如表2、表3和表4所示。

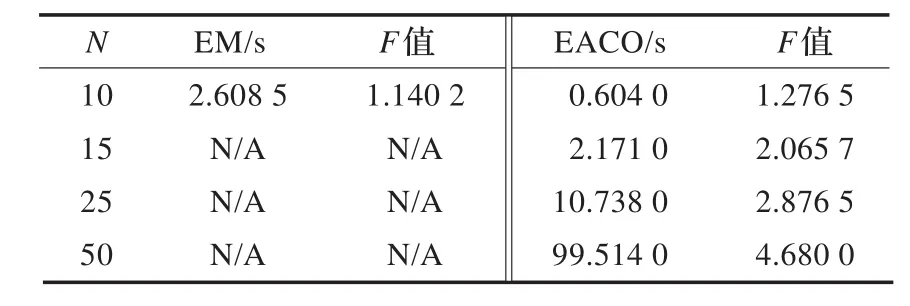
表2 EM算法和EACO算法实验结果

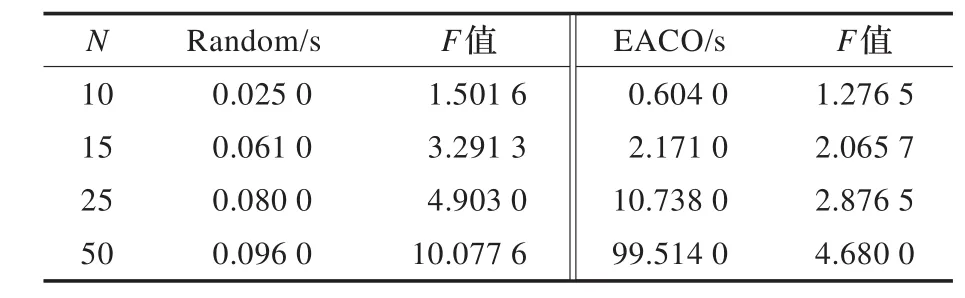
表3 Random算法和EACO算法实验结果

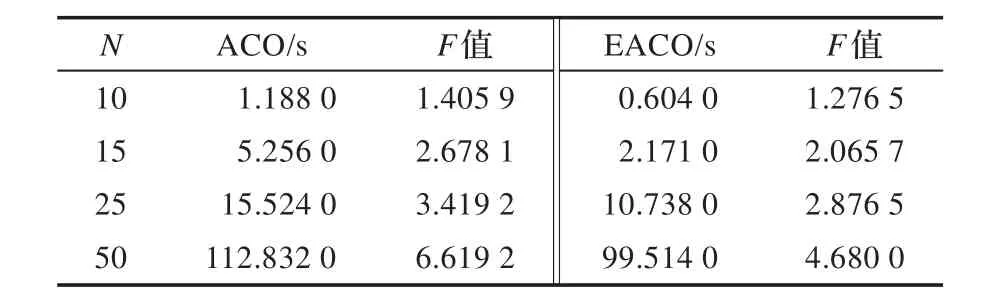
表4 ACO和EACO算法实验结果

基于学习者的学习能力、兴趣爱好和理解水平，使用穷举法和文献[6]中提出的蚁群算法在时间性能上均不如EACO算法，而随机选择法虽分组速度很快，但因缺乏分组的教育学理论依据，导致分组性能太差。

5 结束语

基于学习者的学习能力、兴趣爱好和理解水平，本文采用改进蚁群算法对学习者进行分组，分组性能通过组内均方差来判断，该值越小，则各小组内个体特征相似度越高，即分组越有效。实验中选用了三组模拟数据集进行测试，结果表明本文算法较传统算法分组结果更准确。此外，从教育学角度而言，通过EACO算法将学习能力、兴趣爱好和理解水平接近的学习者分在同组，有助于学习者之间更充分、有效地交互进而提高学习效率。教育者也可根据教学目标的不同，基于EACO算法考虑多个不同的学生特征及其权值分配。但对于大规模学习者分组问题，本文算法需要的求解时间有待进一步缩短。

[1]M cCombs B L，Pope J E.学习动机的激发策略[M].伍新春，秦宪刚，张洁，译.北京：中国轻工业出版社，2002：70-85.

[2]李洁，李克东.CSCL中协作小组分组系统的设计与开发研究[D].广州：华南师范大学，2005.

[3]Huxham M，Land R.Assigning students in Group Work projects：can we do better than random?[J].Innovations in Education and Training International，2000，37（1）：17-22.

[4]Lou Y.within-class grouping：a meta-analysis[J].Review of Educational Research，1996，66（4）：423-458.

[5]M oreno J，Ovalle D A，Vicari R M.A genetic algorithm approach for group formation in collaborative learning considering multiple student characteristics[J].Computers&Education，2012，58（1）：560-569.

[6]Bekele G S.Forming heterogeneous group for intelligent collaborative learning systems with ant colony optimization[C]//Proceedings of the 8th International Conference on Intelligent Tutoring Systems，Taiwan，China，June 26-30，2006，4053（22）：217-226.

[7]Hwang G J.An enhanced genetic approach to composing cooperative learning groups for multiple grouping criteria[J].Educational technology&Society，2008，11（1）：148-169.

[8]Lin Y T.An automatic group composition system for composing collaborative learning groups using enhanced particle swarm optimization[J].Computers&Education，2010，55（4）：1483-1493.

[9]Gall M D.Discussion method[M]//Dunkin M J.The International Encyclopedia of Teaching and Teacher Education.Oxford，England：University of Oxford，1987：232-237.

[10]段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005：108.

[11]Johnson D W.Cooperation in the classroom[M].Edina，MN：Interaction Book Company，1984：101-118.

[12]Slavin R E.Cooperative learning：theory，research，and practice[M].Boston：Allyn and Bacon，1995：180-195.

[13]Yang S JH.Context aware ubiquitous learning environments for peer-to-peer collaborative learning[J].Journal of Educational Technology&Society，2006，9（1）：188-201.

[14]Wang D Y.DIANA：a computer-supported heterogeneous grouping system for teachers to conduct successful small learning groups[J].Computers in Human Behavior，2007，23（4）：2-14.