基于相似关系向量的改进ROUSTIDA算法

丁春荣，李龙澍

1.安徽农业大学信息与计算机学院，合肥230036

2.安徽大学计算机科学与技术学院，合肥230039

1 引言

粗糙集[1]理论是由波兰科学家Paw lak在1982年提出的一种处理模糊、不精确知识和不完备信息的数学工具，在机器学习、数据挖掘等多个领域得到了广泛的应用。由于在现实中存在测量误差、条件受限或不慎遗漏等种种因素，人们往往会得到部分数据缺失的不完备信息系统，如何对缺失数据进行必要的补充，这对信息系统的后续处理如属性约简、规则提取等操作具有非常重要的意义，展开这方面的研究也变行尤为重要。根据粗糙集理论中数据的不可分辨关系对缺失数据进行补齐处理，是目前常用的有效填补方法，这种填补法尽可能地表现出信息系统的基本特征的隐含规律。其中，最具有代表性的补齐算法是ROUSTIDA算法[2]。该算法对于所有的缺失属性同等对待，补齐时按满足条件的先后顺序进行，容易引入决策冲突信息，并且在一些特殊情况下处理到一定的步骤后，会无法继续填补下去。当前，针对ROUSTIDA算法存在的缺陷它进行了广泛研究。文献[3-4]基于决策独立的原则，对ROUSTIDA算法进行改进，使样本X在决策规则缺失时，选择与其相似的无任何缺失值的对象的决策属性值进行填补，消除了填补后潜在的矛盾项；文献[5]提出基于差异关系矩阵的数据补齐算法；文献[6]提出了基于填补顺序的补齐算法。K ryszkiewicz[7-8]于1998年提出粗糙集中对象之间存在着相似关系，指出相似关系也是一种容差关系；在此基础上，文献[9-12]利用量化相似关系的理论，将样本间容差关系引入ROUSTIDA算法中，从而提高了缺失数据的填补效率。本文在保持ROUSTIDA算法良好的填补性能的基础上对其进行了改进，提出一种基于相似关系向量的改进算法，为了尽量避免不一致决策表的产生，算法优先填补决策属性，并在决策属性相同时填补条件属性缺失值，扩展了原算法的使用范围。通过实例说明改进的算法能有效提高补齐数据的准确率，同时尽可能避免了决策规则冲突问题，在一定程度上降低了时间复杂度。

2 粗糙集理论基础

定义1 量化相似关系[2]对于不完备信息系统S=(U，A，V，f)，A=C∪D是属性集合，C∩D=φ，其中C={a1，a2，…，am-1}是条件属性集，D={am}是决策属性集，其中论域U={x1，x2，…，xn}，假设各属性可能取值呈均匀分布，对于∀ak∈A，其值域Ek=，对于任意对象xi∈U，有ak(xi)=的概率为1/|Ek|。因此给定两个对象xj∈U，ak(xj)=，则对于ak(xj)=，xi在属性ak上近似于xj的概率为：

则对象xi和xj在属性ak所有取值上的联合概率为：

通过量化相似关系定义可看出，R(xi，xj)可以度量对象xi和xj在属性ak上的相似程度。对于一个决策信息系统而言，如果两个对象条件属性完全相同，应尽量保持其决策属性一致，以避免不相容决策，即尽量使决策规则相容，这个规则称为决策规则独立原则。由于不相容决策对以后的决策过程有较强的负面影响，因此在对决策属性存在缺失数据的信息系统进行填补时，应尽量遵循这个原则，避免出现不相容的决策规则。如果以定义1中所述的量化相似关系为基础构建可辨识矩阵对ROUSTIDA算法进行改进，填补结果也容易出现决策规则不相容的结果，因此，下面对量化相似关系进行了进一步的修改。

定义2 对于不完备信息系统S，am是决策属性，其值域为Ek=，则对象xi和xj在决策属性am上的决策相容关系定义为：

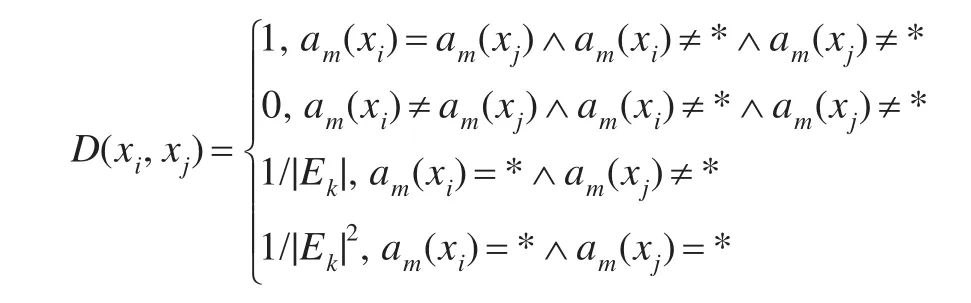
定义3 对于不完备信息系统S=(U，A，V，f)，可定义一个二元组作为量化相似关系向量L=(R，D)，其中R是定义1中的量化相似关系，D是定义2中的决策相容关系。

根据量化相似关系向量构建量化相似关系矩阵如下所示。

定义4 量化相似关系矩阵M定义：

其中i，j=1，2，…，n，L(xi，xj)=(R(xi，xj)，D(xi，xj))。

矩阵中每个元素表示了相应两个样本对象的相似程度。

定义5 对于信息系统S，A={ak|k=1，2，…，m}，是属性集，设xi∈U，对象xi的缺失属性集MASi和信息系统S的缺失对象集MOS定义如下：

对象xi的最大相似对象集NSi定义如下：

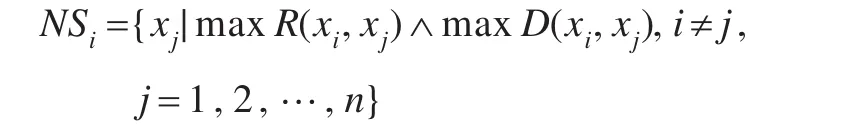
NSi是与对象xi相似度最大的对象集合。

3 基于相似关系向量的改进ROUSTIDA算法

由于不完备信息系统中缺失值的数量及分布不同，因此在许多情况下无法仅仅通过对初始扩充矩阵的一次运算就能补齐所有的缺失数据，往往需要经过多次对扩充可辨识矩阵进行计算和完整化分析才能得到完备的信息系统。因此，可以设初始的信息系统为S0，相应的扩充可辨识矩阵为M0，对象xi的缺失属性集为MA，初始无差别对象集为N，初始缺失对象集为MOS0。第r次完整化分析后的信息系统为Sr，则相应的Mr计算满足以下定理：

定理1 设Mr+1=(Mr+1(i，j))n×n，r=0，1，…，则Mr+1(i，j)计算如下：

由上面定理可看出，数据填补过程中得到的信息系统Sr，其可辨识矩阵不需要重新建立，只要对Sr-1的Mr-1根据缺失数据的填补修改局部元素即可，从而大大降低了计算复杂性。

基于相似关系向量的改进ROUSTIDA算法步骤如下：

步骤1 对初始信息系统S0计算M0、MOS0和MA。

步骤2 （1）对于所有i∈MOSr，计算N。

（2）产生Sr+1：

①对于i∉MOSr，则，k=1,2,…,m；

②对于∀i∈MOSr，对所有ak∈MASri做如下操作：

（i）如果存在j0和j1∈满足(ak(xj0r)≠*)∧

(ak(xj1r)≠*)∧(ak(xj0r)≠ak(xj1r))，则ak(xr+1i)=*；

（ii）否则，如果仅存在一个j0∈NSri，满足ak(xrj0)≠*，

（iii）否则，如果∀j∈NSi，都有

（3）如果Sr+1=Sr，则结束循环转步骤3；否则，对Sr+1计算Mr+1、MOSr+1和，r=r+1，转步骤2。

步骤3 如果信息系统还存在缺失值，可用取属性中平均值（数字型）或最多出现值（符号型）的方法进行填补。

步骤4 结束。

4 仿真实验

仿真实验样本选自文献[13]中水泥窑控制算法表的部分样本，如表1所示。分别采用ROUSTIDA算法和本文改进ROUSTIDA算法对实验样本进行补齐操作，补齐后的信息表结果如表2和表3所示。

4.1 结果分析

由表2可看出，经ROUSTIDA算法补齐后，出现了实例x1与x2，x8与x9相互矛盾的情况，这是因为由原ROUSTIDA算法的可辨识矩阵M0可得出={1，3}，，={6，9}，={7，8}，算法执行到步骤2进行填补时，对于如果存在j0和j1∈满足，则。根据这个条件，算法执行完步骤2后，每个有缺失值的对象都无法对缺失值进行填补，所以得到S1=S0，结束填补循环转向步骤3。假设采用M ean Com pleter算法对所有对象a4属性值进行填补，得到2.5，无论a4的值取2还是取3，都后导致实例x1与x2，x8与x9相互矛盾的结果。从实例可以看出，ROUSTIDA算法存在的不足之处有：

（1）由于无差别对象集NSi定义的局限性，导致算法实际上要经过多次对扩充可辨识矩阵的计算和完整化分析，才能满足终止条件。

（2）决策属性的重要性没有体现出来，这样在填补过程中，容易导致决策规则冲突。

而采用本文提出的基于相似关系向量的改进ROUSTIDA补齐算法完全可以避免在补齐后导致决策冲突的结果。这是因为改进补齐算法每次在对缺失属性值时行填补时，都是在决策属性相同的前提下选择最相似的对象对缺失属性进行填补，有效地避免了决策规则矛盾问题，同时每次循环都能够对更多的缺失值进行充分的填补，因此降低了算法的时间复杂度。

4.2 时间复杂度分析

ROUSTIDA算法的时间复杂度为O(n2×k×p)，p为何能迭代的次数，当存在大量数据时，每轮循环结束后都要重新计算扩充可辨识矩阵M，对算法的时间性能造成很大的影响。而改进的算法对扩充辨识矩阵进行了大幅度的减化，每个矩阵元素都是一个二元值，不仅在很大程序上减少了扩充矩阵的维数，减少了临时存储空间，同时也减轻了后面算法的运算量，改进后的算法的时间复杂度是O(n2×p)。

4.3 算法比较

为了进一步测试新算法性能，从UCI国际机器学习数据库[14]中选择Echocardiogram、Hepatitis和House等3个数据集作为测试集，利用高斯正态分布随机函数，随机抽取50%的样本作为训练集。测试标准为：对于同一个样本，如果根据不同的规则能推出不同的结果，或者根据已有决策规则无法判断其决策属性，均判定为识别错误。对比算法采用ROUSTIDA算法、概率法和特定值法。算法的填补正确率为预测值正确的样本数量/缺失数据样本总数，实验3次，测试结果如表4所示。

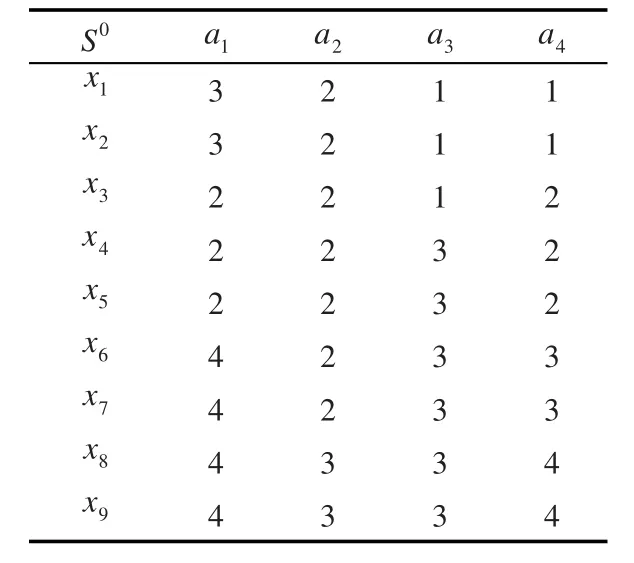
表3 用本文算法补齐的信息表

表1 水泥窑控制算法表部分样本

表2 ROUSTIDA算法补齐后信息表

表4 算法的平均填补正确率（%）

影响填补正确率的主要因素是训练集所能提供的数据关系及内在规律是否足够，比如House数据集由于各数据之间的内在关系较为紧密，因此填补正确率要高于同样缺失率的Hepatitis数据集，而Echocargiogram数据集的数据内在规律相对较少，因此即使含有缺失值的样本所占比例并不多，但填补正确率却不高。

5 结束语

针对ROUSTIDA算法的不足提出一个基于相似关系向量的改进ROUSTIDA算法。首先，本文算法优先填补决策属性，在决策属性相同的前提下再选择相似度最大的对象对缺失属性进行填补，因为对于每个存在缺失值的对象而言，相似对象的近似概率不尽相同，所以填补后有效地减少了数据填补导致的决策规则矛盾问题。其次，相似关系向量矩阵的元素是由向量构成，因此比原ROUSTIDA算法中的扩充可辨识矩阵要简化，从而降低了空间复杂度。最后，在数据补齐过程中，由于每次选取相似度最大的对象对缺失属性进行填补，提高了每次循环的补齐数目，加快了算法的收敛速度，对于数据量大，属性较多，缺失属性值也较多的信息系统而言，该算法在一定程度上降低了时间复杂度。因此，本文算法对于数据量大、属性较多的不完备信息系统而言不失为一种良好的补齐算法。

[1]Paw lak Z.Rough sets[J].International Journal of Computer Information Science，1982，11：341-356.

[2]王国胤.Rough集理论与知识获取[M].西安：西安交通大学出版社，2001：46-97.

[3]张振化，刘文奇.一种基于粗糙集理论不完备数据的改进算法[J].计算机科学与工程，2002，24（2）：41-42.

[4]田树新，吴晓平，王红霞.一个基于改进的ROUSTIDA算法的数据补齐方法[J].海军工程大学学报，2011，23（5）：11-15.

[5]潘巍，王阳生，杨宏戟.粗糙集理论中新的针对不完备信息系统的处理方法研究[J].计算机科学，2007，34（6）：158-161.

[6]刘伟.基于粗集理论不完备数据的改进算法[J].吉林师范大学学报：自然科学版，2007，8（3）：113-114.

[7]K ryszkiewicz M.Rough set approach to incomplete information system[J].Information Sciences，1998，113（3/4）：274-292.

[8]K ryszkiewicz M.Rules in incomplete information system[J].Information Science，1998，113（3/4）：274-292.

[9]朱小飞，卓丽霞.一种基于量化容差关系的不完备数据分析方法[J].重庆工学院学报，2005，19（5）：23-25.

[10]张在美.一种基于粗糙集的不完备信息处理方法研究[D].长沙：湖南大学，2007.

[11]秦华妮.基于量化相似关系的不完备决策信息系统的完备化算法[J].湖南工程学院学报，2007，17（1）：65-67.

[12]李萍，吴祈宗.基于概率相似度的不完备信息系统数据补齐算法[J].计算机应用研究，2009，26（3）：881-883.

[13]曾黄麟.粗集理论其及应用——关于数据推理的新方法[M].重庆：重庆大学出版社，1998：153-154.

[14]Blake C M.UCI machine learning repository[DB/OL].（2005）[2012-06-01].http：//www.ics.uci.edu/～m learn/M LRepository.htm l.