基于M IMO技术的DCSK通信方案的性能分析

何世彪，韩彦净，张青，杨迷

重庆大学通信工程学院，重庆400044

1 引言

本文所研究的内容是关于混沌数字调制方案，将混沌数字调制与分集技术相结合，以提高混沌通信系统的抗噪声性。早期提出的CSK通信系统采用基于混沌序列同步的相干检测方法，具有较好的误码性能。但在实际通信环境中，由于混沌信号对初始条件的极端敏感性，若利用信道传输中引起畸变的信号驱动接收端系统实现混沌同步，进行可靠通信，仍然存在较大困难，阻碍了CSK通信系统的实际应用。而DCSK通信系统不需要混沌同步，且在各种混沌键控数字调制方案中，DCSK是研究最多的一种混沌调制方案，具有很好的抗噪性能，同时又利用了混沌信号的类似噪声特性，达到了隐藏信号的目的，因此成为混沌通信研究的热点方向之一。但是这些系统很少涉及无线通信环境中普遍存在的高斯白噪声干扰现象[1]。文献[2]分析了非相干DCSK通信系统在高斯白噪声信道下的误码性能，结果表明DCSK通信系统的误码性能并不理想，系统本身的抗噪声性能有限。分集接收是一种在无线通信系统中广泛使用的技术，可以增强通信系统的抗噪声性。本文讨论的内容主要是以DCSK为基础的M IMO-DCSK混沌通信方案。前人的研究主要针对的是单输入单输出（SISO）的混沌通信系统。然而，在无线通信系统中，信道噪声是影响SISO-DCSK混沌通信的主要原因之一，而近年来提出的M IMO技术就是一种能够有效改善信道性能的方案之一。同时在M IMO信道中利用多天线传输信息信号是一个热门话题，它可以对抗无线通信系统中普遍存在的信道噪声。

另一方面，文献[3]对M IMO技术进行了较为详尽的分析研究，证明了M IMO技术能够有效地改善信道性能，为M IMO技术在通信中的应用奠定了一定的研究基础。文献[4]也研究了SIMO-DCSK混沌通信方案的可行性，然而针对M IMO-DCSK混沌通信的研究较少。因此，本文结合M IMO技术与DCSK混沌调制技术各自的优点，设计了M IMO-DCSK混沌通信方案，研究了实施M IMO信道下DCSK通信方案的可行性。结合该系统文章研究了信息传输中的误码性能，通过理论分析和仿真研究得到了在不同条件下DCSK通信系统、M IMO-DCSK通信系统的误码率对比图。结果表明，和传统DCSK通信系统相比，使用M IMO技术的DCSK通信系统的误码性能有了较大的提高。

2 DCSK混沌通信系统原理

差分混沌键控（DCSK）是由Kolumban在1996年提出的一种具有稳健特性的非相干接收技术，此后一种优化的频率调制DCSK（FM-DCSK）被提出。由于其原理简单，便于分析和实现，并且在多径信道中也有较好的稳健性，因而引起了混沌通信研究人员的普遍关注。目前该技术已被列入欧盟委员会的长期研究计划。

DCSK方案如图1所示[5]，发送的每一个比特信号由两个混沌抽样函数表示，第一个作为参考信号，第二个用来承载信息。如果发送的符号为“1”，那么第二个抽样函数和参考信号相同；如果发送的是“-1”，那么第二个发送的信号和参考信号相反。在接收端参考信号和信息信号进行互相关后判决解调。

图1 DCSK系统框图

第l个发送的信号可表示为：

其中，xk是第l个信息比特参考信号段的混沌序列，xk-β是延时后的信息承载段的混沌序列。

3 M IMO-DCSK混沌通信方案

3.1 M IMO-DCSK系统设计

文中采用的混沌映射是改进型Logistic序列：

由于该映射产生简单，相关性好，因此文中仿真都采用改进型Logistic序列。此外，该混沌序列的均值为0，方差为1，即E[xk]=0，var[xk]=1。

文献[6]首次提出了M IMO-DCSK混沌通信系统的设计。本文考虑具有2个发送和2个接收天线的天线系统。空时编码采用空时分组码（STBC），STBC码作为一种发射分集技术，能有效抵抗衰落，在独立信道下性能最佳。

3.1.1 发送端设计

在A lamouti的空时编码中，先调制每一组m(m=lb M)个信息比特，然后通过串并转换，编码器在每一次编码中选择两个调制符号s1和s2为一个分组，并根据如下给出的编码矩阵将它们映射到发射天线：

编码器的输出在两个连续的周期t和t+Tb里，从两根发射天线发射出去。在第一个周期中，信号s1和s2同时从天线1和天线2分别发射出去；在第二个周期内信号-从天线1发射，而信号从天线2发射出去。很显然，这种方法是在空间域和时间域进行编码，分别用S1和S2来表示天线1和天线2的发射序列：

图2（a）是DCSK调制技术结合STBC编码方法设计的发送模块框图，表1给出了在时间2Tb=4Tc内的传输信号的结构。

3.1.2 信道设计

2个发送天线Tx1和Tx2分别经过衰落信道的增益h11、h12、h21、h22，并叠加上高斯信道白噪声后，由两个接收天线Rx1、Rx2接收，之后分别送往接收端进行相关接收和判决。

3.1.3 接收端设计

图2（b）设计了接收模块框图，在接收端，经过信道之后，噪声与干扰信号一起被接收。接收信号首先由相关接收器进行相关接收，然后经过STBC解码器进行解码。由于2个接收天线有着相似的形式，在表2中只给出了天线1的接收序列表达式，其中h11、h21为信道增益。

由此结合STBC设计了M IMO-DCSK混沌通信的系统框图，如图2所示。

图2 基于时空编码的2×2M IMO信道的DCSK系统框图

表1 发送端的信息序列

表2 接收端的信息序列

3.2 M IMO-DCSK系统误码性能分析

为了简化数学分析，假设时间Tc=1，则在时间[0，β]后相关器1的输出y11的表达式为：

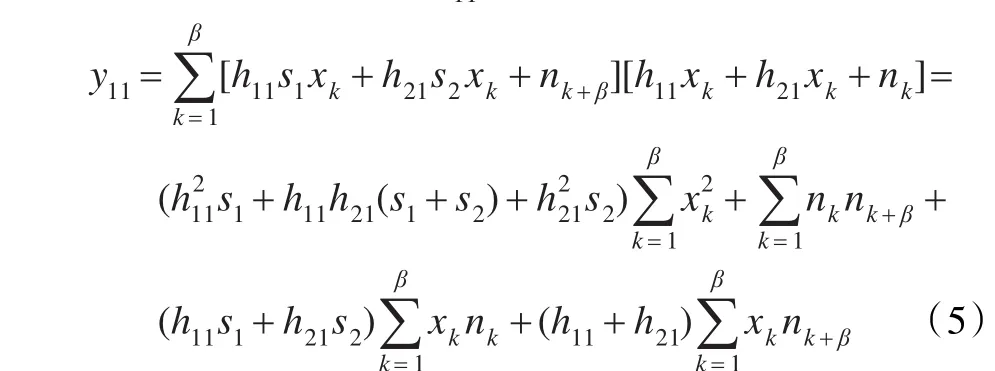
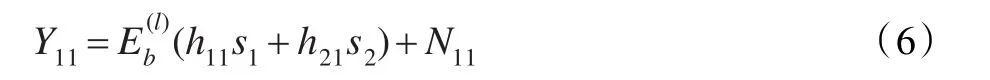
其中N11是均值为零的高斯白噪声。

相应地可以得出Y12，Y21，Y22的表达式，所以接收信号Y可以表示为：

上式也可写为向量形式：

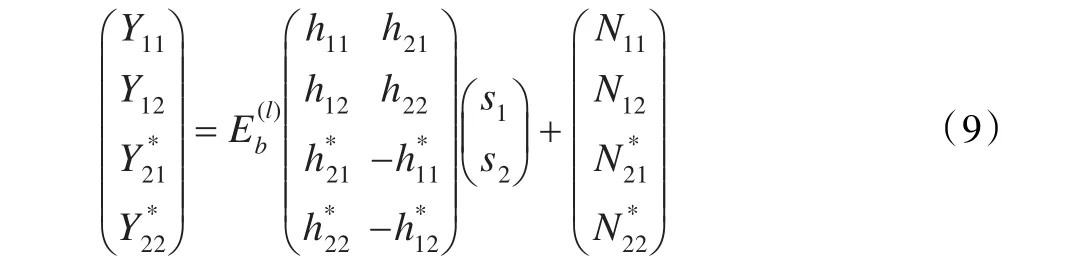
本文主要研究M IMO-DCSK通信系统在AWGN信道下的误码率性能，因此信道增益假设为常数且为1(hij=1)。

采用空时解码公式（10）对接收到信号Y进行解码，从而得出传输的信息比特。

上式第一项与第二项是相等的，其中向量N中的每个元素Nij是互不相关的且与混沌序列相互独立，高斯噪声的每个样本也是独立的，将Nij的表达式代入式（14）可得：

综上推导可得第l个信息比特的方差为：

假设每比特的能量是固定的，可以得出第l个信息比特的误码率为：

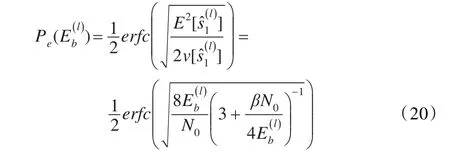
文中采用高斯近似法[7]计算发送端的信息比特的能量，由于混沌信号的非周期特性，传输的信息比特的能量在混沌扩频后不断变化。因此，M IMO-DCSK通信系统的BER表达式为：

为了计算式（21）需要得到每比特信息所对应的混沌序列的能量分布图，图3为β=5时改进型Logistic混沌序列的能量分布的拟合图。

由于能量分布的概率密度函数的解析表达式很难获得，数值积分仍然是误码率计算的一种有效方法。考虑到每比特的能量变化，数值积分表达式如下：

图3 β=5时能量分布的拟合直方图

4 仿真分析

在M atlab/Simulink环境中搭建仿真模型，在高斯白噪声信道下仿真该M IMO-DCSK混沌通信系统。仿真模型中，用改进型Logistic映射作为混沌序列发生器，扩频因子分别取β=5，β=50，系统的基带数据速率为200 Kb/s，采用2个发射天线和2个接收天线的M IMO通信信道。采用M onte Carlo法仿真DCSK、M IMO-DCSK通信系统，在统计误码率时，每一种Eb/N0仿真100 000个符号点数，仿真中信噪比取值范围是[0 dB，10 dB]，以1 dB递增。图4、图5、图6是在高斯近似下的理论与仿真误码率曲线，可以清楚地看到M IMO-DCSK通信系统相比于DCSK系统的误码率性能得到了很大的提高。

图4的仿真结果表明在扩频因子较小的时候，计算BER表达式（22）得出的理论误码率与仿真得出的误码率轨迹有一定的差别。图5表明当扩频因子较大的时候，每比特信息的能量变化很小，计算BER表达式得出的理论误码率与仿真得出的误码率轨迹差异较小。比较图4、图5可以看到，扩频因子(β=50)较大时，M IMODCSK通信系统的噪声性能比扩频因子(β=5)较小时的噪声性能差。而图6则表明，对于给定的Eb/N0，随着扩频系数的增大，DCSK通信系统存在一个最佳的扩频系数使其误码率最小，而M IMO-DCSK通信系统的误码率则呈现增大的趋势。综上可得，M IMO-DCSK通信系统相比于DCSK系统的误码率性能有较大的提升，从而也验证了本文方法的优越性。

图4 β=5时，DCSK、M IMO-DCSK系统误码性能的理论与仿真比较图

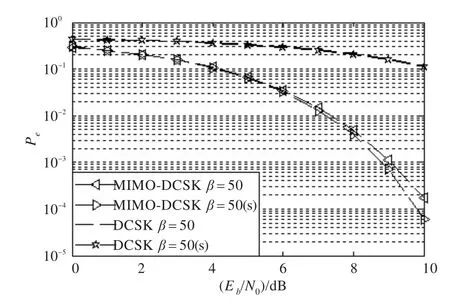
图5 β=50时，DCSK、M IMO-DCSK系统误码性能的理论与仿真比较图

5 结论

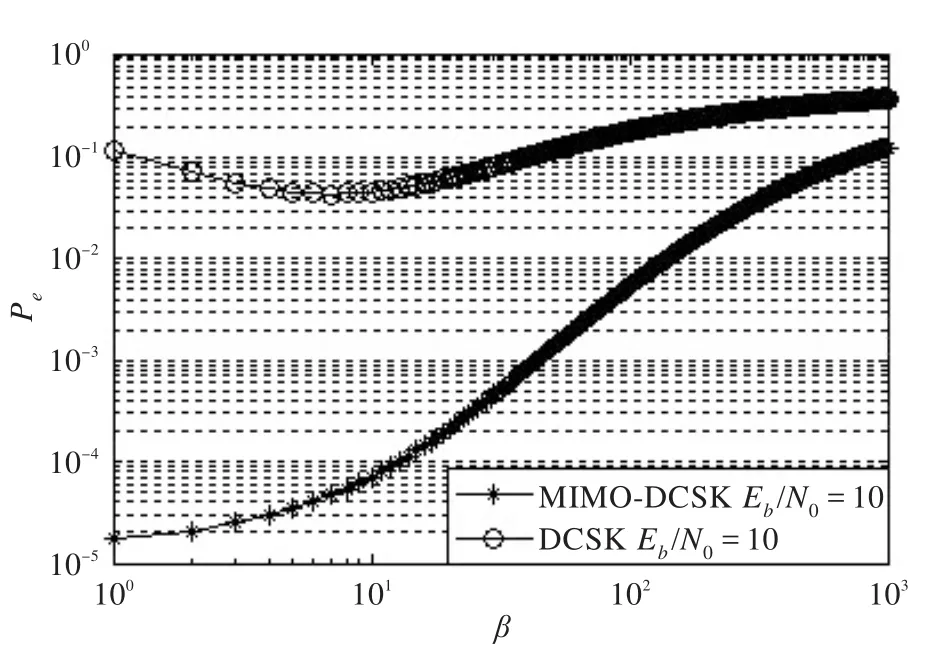
图6 不同β下DCSK、M IMO-DCSK系统的理论误码性能比较图

提出了一种M IMO-DCSK混沌通信方案，并与DCSK系统的性能做了比较。新的混沌通信方案采用了2个发射天线和2个接收天线，在高斯白噪声信道中进行传输，同时利用DCSK不需要混沌同步的优点，通过仿真可以看到，在扩频因子相同的情况下，M IMO-DCSK通信方案相比于DCSK通信方案具有更好的噪声性能，且随着扩频因子的增大，误码率性能随之增大。由此可看出，M IMO-DCSK混沌通信系统有效地改善了信道特性，提高了信息在传输中的安全性，其在瑞利衰落信道下的误码率性能有待进一步的研究。

[1]陈宏滨，冯久超，胡志辉.一种DCSK通信系统的延迟合并接收方案[J].物理学报，2007，56（11）：6270-6275.

[2]Kaddoum G，ChargéP，Roviras D，et al.Performance analysis of differential chaos shift keying over an AWGN channel[C]//Proceedings of IEEE International Conference on Advances in Computational Tools for Engineering Applications，2009：255-258.

[3]胡峰，周德扬.M IMO正交空时分组码技术[J].中国传媒大学学报，2011，18（4）：24-30.

[4]张朝贤.SIMO FM-DCSK无线通信系统研究[D].厦门：厦门大学，2008.

[5]王振朝，张士兵.DCSK的反相叠加相关解调方案[J].计算机工程与应用，2011，47（15）：145-147.

[6]Ma Huanfei，Kan Haibin.Space-time coding and processing with differential chaos shift keying scheme[C]//Proceedings of IEEE International Conference on Communications，2009.

[7]Kaddoum G，ChargéP，Roviras D.A generalized methodology for bit-error-rate prediction in correlation-based communication schemes using chaos[J].IEEE Communication Letters，2009，13（8）：567-569.