基于演化图论的可靠的VANETs路由协议

卢进军，龙英艳，潘宏利

1.陕西理工学院物理与电信工程学院，陕西汉中723000

2.陕西理工学院教育科学学院，陕西汉中723000

1 引言

每天，有许多人死于交通事故，为此，车载网VANETs（Vehicular Ad hoc Networks）的研究得到广泛关注。通过VANETs分发道路安全消息，预防交通事故。因此，VANETs也被认为是应用于道路车辆通信的最有前途的技术之一[1]。VANETs是移动自组网MANETs（M obile Ad hoc Networks）一种特殊形式，能实现车辆间的通信。在网络中的每个车辆，能收、发以及向其他车辆转发消息。通过这种方式车辆能交互实时的交通信息，有利于用户安全驾驶。与MANETs不同，VANETs具有独特的特性，如高的传输功率，高的计算能力，节点的高速移动、移动预测性以及网络拓扑动态变化等[2]。这些特性给部署VANETs提出挑战，尤其是，节点的高速移动和拓扑动态变化[3-4]。

在VANETs中，将车辆看成顶点（vertices），车辆间通信链路看成边（edge），并引用图论（graph theory）以理解VANETs的拓扑特性。文献[5-6]针对可预测的移动模型，提出采用演化图形获取动态网络的移动信息。这一成果在MANETs以及延时容忍网络（delay-tolerant networks）[7]显示了不错的性能，然而，演化图论不能直接应用于VANE Ts。

为此，本文以高速公路的车辆为分析对象，并假定车辆以匀速行驶，对演化图论进行改进，并利用改进后的图论形成VANETs通信图，在此基础上，提出基于演化图论的可靠的VANETs路由协议。

2 相关研究

文献[8-9]分析了VANETs中的路由可靠性。对于VANETs，Taleb等[10]提出了基于车辆行驶方向的路由方案。该方案利用车辆方向信息预测链路寿命，在链路断裂前进行切换新的链路。根据车辆移动方向组群，并从同一个群构建链路。如果车辆改变了行驶方向，就意味着由该车辆建立的链路有可能断裂。

文献[11]提出速度辅助路由协议。该协议利用转发节点与目的节点的相对速度信息决策数据包的转发路径。通过目的节点的位置以及速度预测目的节点下一时刻的位置，并据此明确数据包的转区域。

文献[12]利用了高速公路车辆移动模型的可预测性，提出基于预测路由PBR（Prediction-Based Routing）方案。PBR预测路由寿命，并预先切换即使断裂的路由。通过车辆的通信范围、位置以及速度计算链路的寿命，PBR选用寿命最长的链路组建路由。

文献[13]提出基于移动预测路由协议MOPR（Movement Prediction-based Routing）。MOPR预测车辆下一时刻的位置从而发现稳定的路由，当源节点与目节点间存在多条通路时，MOPR就从中选取最稳定的路由传输数据。

此外，一些研究在MANETs和VANETs引用演化图论分析动态网络的特性。文献[14]利用演化图论模型评估MANETs的最小的路由开销，并利用网络仿真软件NS2实现演化图论；文献[15]着重分析了VANETs通信图形的统计特性，并针对网络动态特性进行了全面的分析。

3 车辆可靠性模型

在高速公路上，车辆常以高速行驶，这为建立可靠路由方案增添了不少困难。路由的性能受多个因素影响，例如，车辆的移动模型以及车辆分布均是影响路由的因素[16]。为了能建立准确的车辆可靠性模型，首先应确定移动模型以及车辆分布特性。车辆分布的确定有利于预测车辆间通信的持续时间。

3.1 车辆分布

有两个主要方法描述车辆流量的时空传播[17]，分别为宏观、微观流量模型。宏观的流量模型利用聚合的宏观量描述车辆流量，如交通密度p(x，t)，交通流量q(x，t)以及平均速度v(x，t)。x表示空间位置，t表示时间。利用以下等式[18]将这些参数关联一起。

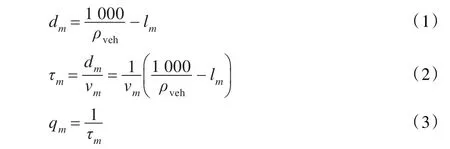
其中，dm表示车辆间平均距离；ρveh表示交通密度；lm表示车辆的平均长度；vm表示车辆平均速度；τm表示车辆间通信的平均用时；qm表示平均交通流量。微观流量模型是将车辆作为独立的个体描述，主要有加速度、减速度以及换道回应周边流量等参数。众所周知，宏观流量模型可描述一般的交通流量状态也可表示个体车辆[19]。因此，本文选用宏观流量模型。接下来，从宏观的角度，利用车辆速度的分布建立链路可靠性模型。

3.2 链路可靠性模型

定义链路可靠性表示车辆间链路在一段时间持续可用的概率。两车辆在时间t，建立了链路l。在时段Tp，链路的可靠性可表示为r(l)：

为了计算链路可靠性，首先应分析车辆速度分布。假定车辆速度服从正态分布[20]，基于这个假设，对于车辆ϑ，其速度的概率密度函数记为g(ϑ)。相应地，G(ϑ)表示概率分布函数。

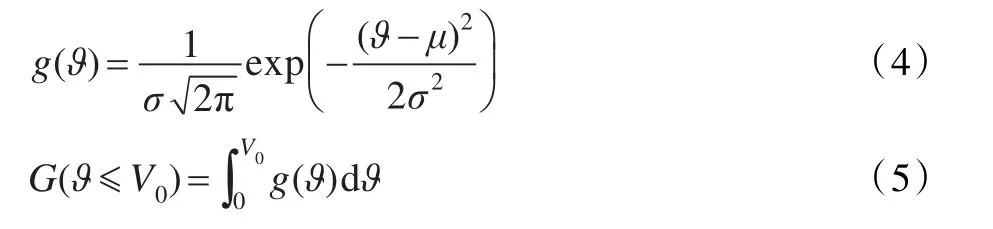
其中，μ、σ2分别表示速度的均值、方差[21]。车辆间距离d可通过车辆的相对速度进行计算。假定车辆的通信范围为R。因此，通信可持续时间T的概率密度函数f(T)可表示为：

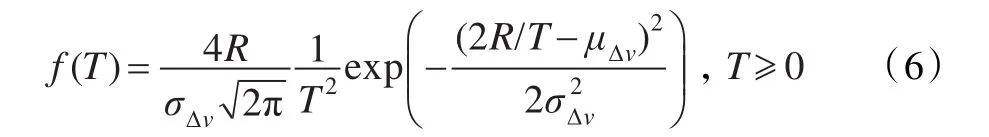
其中，Δv表示车辆相对速度；μΔv、σ2Δv分别是相对速度Δv的均值、方差。

在时间t，车辆i、j形成链路l，链路的寿命Tp可表示为：

其中，Li，j表示车辆i、j间的欧式距离。

3.3 路由可靠性定义

在VANETs中，源节点s与目的节点d可能存在多条路由ω。每条路由由一系列的链路组成。不失一般性，对于某特定的路由P，假定它由k条链路组成：l1=(s，n1)，l2=(n1，n2)，…，lk=(nk，d)。根据式（8），每条链路lm(m=1，2，…，k)的链路可靠值可表示为r(lm)。因此，路由P的路由可靠值Re(P(s，d))：

假定源节点s与目的节点d存在ω条路由。用M(s，d)={P1，P2，…，Pω}为源节点s与目的节点d路由集。在路由决策时，应选取最可靠的路由作为数据转发的通道，即按照式（10）选择路由：

4 面向VANETs演化图论模型

当前的演化图论（Evolving Graph Theory）不能直接应用于VANETs，因为当前演化图论模型并没有考虑通信链路的可靠值。为了满足VANETs的要求，对当前的演化图论进行扩展。扩展后的演化图论模型EEGM（Extended Evolving Graph model）结合了实时交通流量信息，并融入通信链路的可靠性信息。

对于一个特定的图G(V，E)，其子图记为SG=G1(V1，E1)，G2(V2，E2)，…，Gλ(Vλ，Eλ)。因此，。将演化的图论记为G～=(SG，G)，其中，VG～、EG～分别表示G～点、边的集合。

当前的演化图论有三个择选通路的规则[14]：最初的（foremost），最先到达；最短的（shortest），最小跳数；最快的（fastest），最小传输时延。

扩展后的演化图论模型EEGM：

提出的EEGM强调了VANETs的通信图，并考虑通信链路的可靠值。如图1显示了两个时刻的面向高速公路的EEGM的样例。图中的节点表示高速公路上的行驶的车辆。与演化图论不同的时，EEGM对每条边用(t，r(e))标识，其中t表示当前时间，r(e)=r(l)表示链路可靠性，由式（8）计算。

在EEGM中，如果r(e)=0，表示此通信链路无效。设Trav(e)为决策链路e是否能遍历的函数，如式（11）所示：

图1（a）显示了在t=0时每条链路的可靠性值，从图中可知，所有的链路都是有效的，Trav(e)=True。图1（b）显示了在t=5时每条链路的可靠值。从图（a）演化到（b），链路的可靠值发生了变化。注意到{B，E}和{F，G}不再有效，因为在t=5时，r({B，E})=r({F，G})=0。

图1 在t=0，t=5时的EEGM模型

此外，引用新的指标命为通路的可靠值（Journey Reliability）。通过该指标选择转发数据的通路。在数据转发时，选取最可靠的通路（M ost Reliable Journey，MRJ），而不是最初的，最短、最快的通路。

假定有k条边组成一个有效的从节点i到节点j的通路J()i，j。在时间t，边ew的可靠值表示为rt(ew)，w=1，2，…，k。因此，通路的可靠值Re(J(i，j))如式（12）所示：

假定这有n条从节点i到节点j的通路，n条通路的集合表示为MJ(i，j)={J1，J2，…，Jn}。因此，可通过式（13）选取最可靠的通路MRJ：

5 移动模型

本文研究的VANETs场景为高速公路。假设车辆以匀速沿单一方向行驶。根据文献[11]的分析，这个假设是合理的。基于这个假设，每个车辆i设置以下参数：在时间t笛卡儿位置坐标xi(t)和yi(t)；速度vi(t)=v0；移动方向ai(t)=a0。

6 提出的EG-RAODV

为了实现VANETs数据传输的可靠性，结合EEGM的特性，提出新的路由协议。该路由协议利用EEGM的模型，从路由的可靠值的角度选择从源节点到目的节点的最佳路由。提出基于EEGM选择最可靠的MRJ的方案，并将此方案运用到按需式距离矢量路由协议AODV（Ad hoc On-demand Distance Vector）[22]，提出的路由协议记为EG-RAODV。

6.1 EG-Dijkstra算法

在EEGM模型中寻找最可靠的路由，等价于寻找MRJ。常用的Dijkstra算法[23]不能直接应用于本文，为此，将其修改，并提出基于演化图论的Dijkstra算法（EG-Dijkstra）。基于式（11）和（13），利用EG-Dijkstra算法寻找MRJ。

EG-Dijkstra利用可靠图数组RG（Reliable Graph）保存所有车辆以及它们相应的MRJ值。在算法的初始阶段，源节点s为RG(s)=1，其他节点的RG()i=ϕ。图2显示了EG-Dijkstra算法的示例。

假设源节点为图2中标识的节点0，目的节点为节点5，且RG(0)=1。根据式（8）计算每条链路可靠值r(l)。如节点0与节点1间链路可靠值为r(l0)=0.43，l0=(0，1)。根据EG-Dijkstra算法，利用r(l0)与RG(0)相乘，得到下一节点的RG值。如节点0的RG(1)=r(l0)×RG(0)=1×0.43=0.43。节点5的RG(5)=r(l1)×RG(1)=0.43×0.21≈0.09，如图2的（ii）所示。

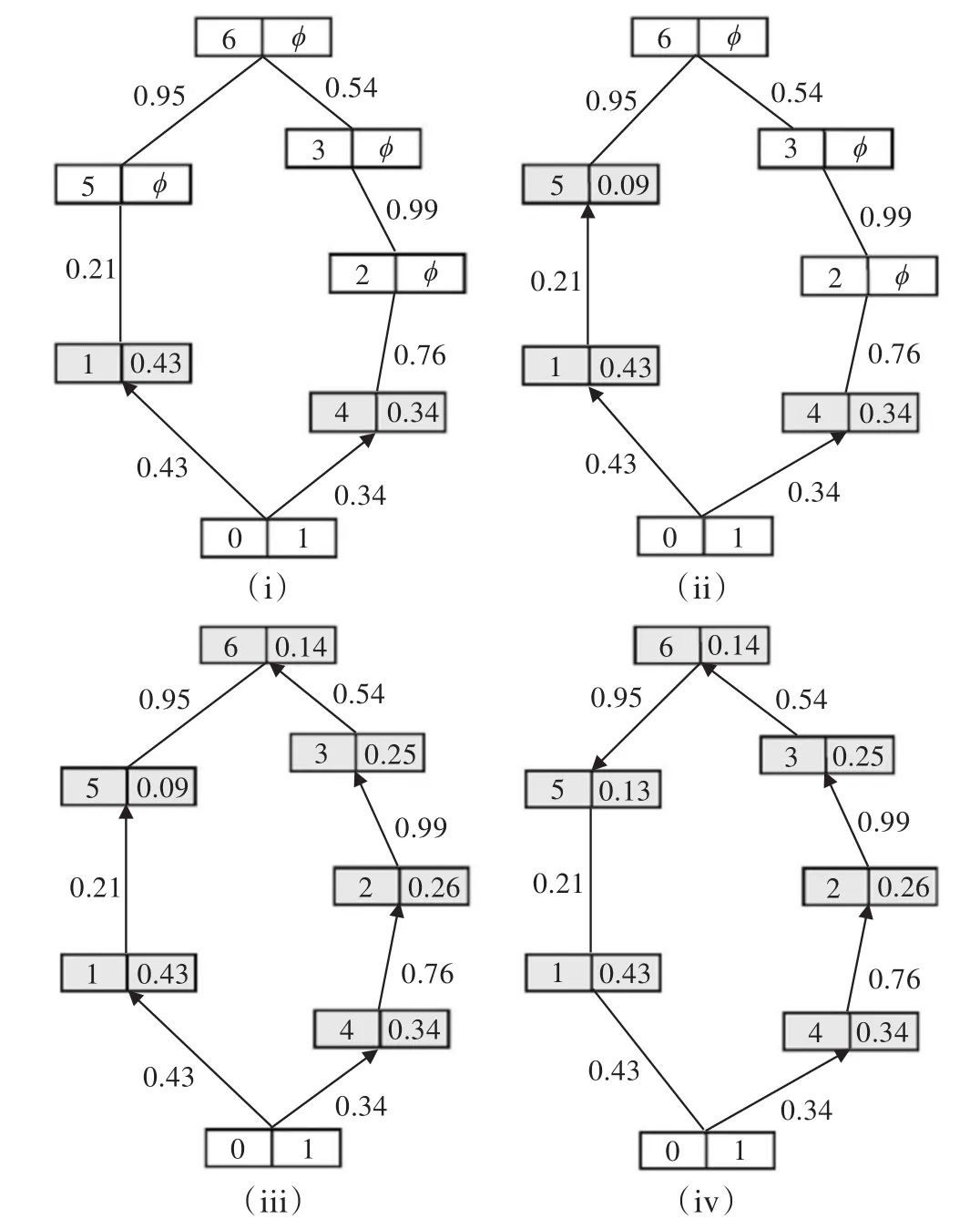
图2 EG-Dijkstra算法的示例

尽管节点5是目的节点，但是EG-Dijkstra算法运行到图2的（ii）并不停止，其需计算所有通路的可靠值，并从中选择最可靠的值，作为数据的路由。从图2可知，有两条通路到达目的节点：第一条0→1→5；第二条0→4→2→3→6→5。第一条通路可靠值为0.09；第二条为0.13，如图2的（iv）所示。这表明第二通路比第一条通路更可靠，为此，选用第二通路作为数据传输的通道。

6.2 EG-RAODV路由特性

假定源节点知晓当前EEGM的状态信息。源节点在时间t需传输数据，源节点先计算EEGM模型中的每条链路的可靠值，并利用EG-Dijkstra算法寻找最可靠的通路MRJ。在获取最可靠的MRJ后，源节点产生路由请求消息RREQ（Routing Request message），并将MRJ的跳数加入RREQ中，即扩展RREQ，存储MRJ的信息。依据MRJ的信息，中间节点转发路由请求，无需广播。

沿途MRJ的车辆收到RREQ，中间节点不需要向目的节点发送路由请求回复消息RREP（Routing Reply message）。只有RREQ到达目的节点，才回复RREP消息。

据上述分析可知，EG-RAODV方案无需广播路由请求，这极大节省了网络资源。此外，EG-RAODV并没有使用hello消息去确认链路的状态，减少了网络负担。在路由维护过程阶段，EG-RAODV使用了与AODV相同的机制。当链路断裂时，发送路由错误消息RERR（Routing Error message），从而实现维护路由并发现新路由的功能。

7 仿真分析

仿真的目的在于评估提出的路由协议的性能。采用OMNet++进行仿真，每一个仿真实验进行50次，取平均值作为仿真的最终数据。将仿真结果与AODV以及PBR进行比较。

7.1 仿真环境

仿真区域为5 000m的三车道高速公路。30辆车（低密度交通流量）分布于仿真区域。车辆仅单方向行驶，到达高速公路末端，就退出仿真区域。三个车道的平均速度分别为40 km/h、60 km/h、80 km/h。针对两个实验场景进行仿真：

（1）实验A数据传输速率从32～512 Kb/s变化；数据包的大小为1 500 Byte。三个车道的车辆平均速度仍为40 km/h、60 km/h、80 km/h。

（2）实验B数据包的大小从500 Byte至3 000 Byte变化；数据传输速率为128 Kb/s。三车道的车辆平均速度仍为40 km/h、60 km/h、80 km/h。

7.2 性能指标

在仿真过程中，利用以下性能指标评估网络性能。

（1）分组传输率PDR（Packet Delivery Ratio）：目的节点成功接受到的数据包数目与在应用层的源节点发送的数据包数目之比；

（2）平均链路断裂数（Average Number of Link Failures）：在路由阶段，链路断裂的平均数目；

（3）路由请求消息率（Routing requests ratio）：路由请求消息占总的路由消息百分比；

（4）平均端到端传输时延E2E（Average End to End delay）：接受到的数据包发送与接收的时间差。

7.3 仿真结果

（1）数据传输速率的变化对路由性能的影响

图3显示分组传输率随数据传输速率的变化曲线。从图3可知，与PBR、AODV相比，提出的EG-RAODV具有最高的分组传输率。此外，EG-RAODV随数据传输率的变化相对较稳定，而PBR和AODV的下降较快。这主要是因为EG-RAODV采用EEGM模型，提高了路由的稳定性；同时EG-RAODV无需广播RREQ，节省了网络资源，为分组传输率提供了更多带宽。

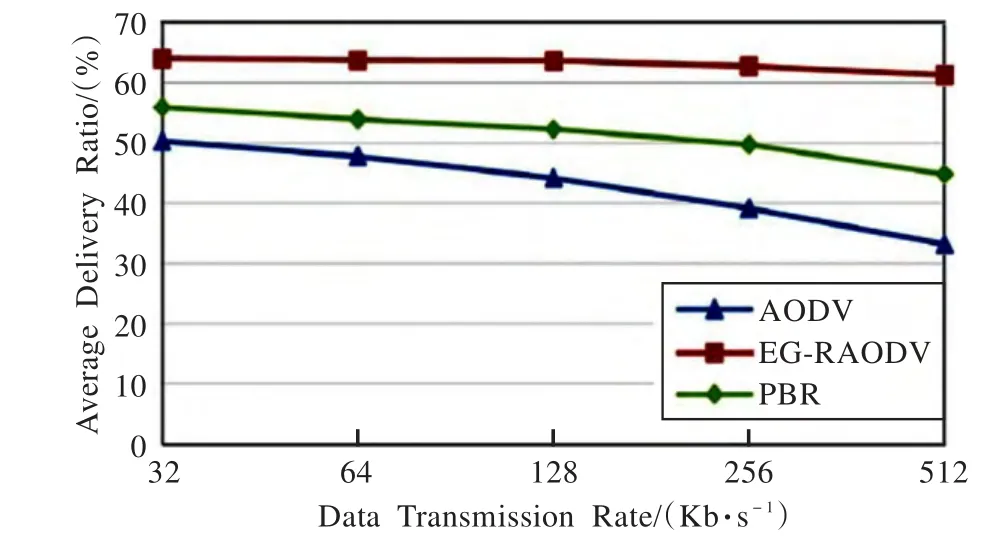
图3 实验A：分组传输率随数据传输速率变化

图4显示了路由请求消息率随数据传输速率的变化情况。与PBR和AODV相比，EG-RAODV的路由请求消息率最小。这主要是因为PBR和AODV需一直广播RREQs直到目的节点，而EG-RAODV只需依据MRJ进行传输，无需广播，大大减少了发送RREQs的数量。

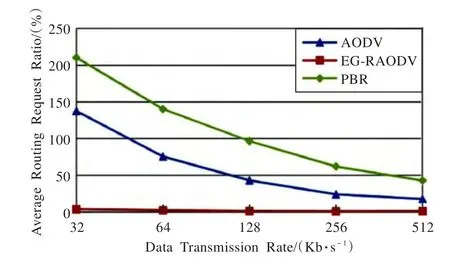
图4 实验A：路由请求消息率随数据传输速率变化

图5显示EG-RAODV、PDR以及AODV的平均链路断裂数随数据传输速率的变化情况。从图可知，EG-RAODV具有最低的平均链路断裂数。AODV最高，这是由于AODV采用最短路径原则选择路由，未考虑链路可靠性。PDR之所以优于AODA是因为PDR采取链路寿命预测机制，在链路断裂前，选用了新的路由。此外，从图5知，数据传输速率越高，EG-RAODV的优势越明显。

图5 实验A：平均链路断裂数随数据传输速率的变化

提出的EG-RAODV的另一个优势体现于平均端到端传输时延，如图6所示。EG-RAODV具有最低的端到端传输时延。这主要是因为EG-RAODV具有整个EEGM的信息，很容易预测其他节点的位置，并能找出最可靠的路由。由于AODV仅采用原始的反应式路由方法建立路由，AODV的端到端传输时延最大。

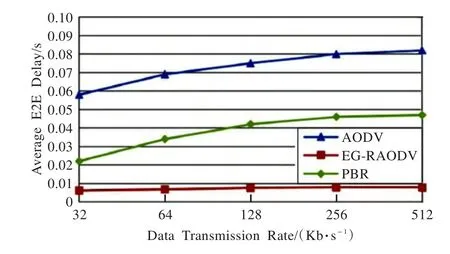
图6 实验A：平均端到端传输时延随数据传输速率的变化

（2）数据包大小的变化对路由性能的影响

如图7所示，EG-RAODV随数据包大小的变化呈现最高的分组传输率，并且稳定。注意大尺寸的数据包可能是分散传输的。在分组传输过程中，任何传输分散数据包链路的断裂都可能导致整个数据包分组传输失败，如果失败，需要重新开始新的路由发现工作。从图可知，EG-RAODV的性能优于AODV，这主要是因为EG-RAODV搜寻了所有到达目的节点的通路，并从中选取最可靠的路径作为数据的传输通路。

图8显示三个协议的平均路由请求消息率的变化情况。PBR路由协议的平均路由请求消息率高于AODV和EG-RAODV。随着数据包尺寸的增大，数据包分散的数量也随之增加。这将引起更多的分组传输失败，从而导致更多的路由请求消息，以建立新的路由。这也正是PBR的平均路由请求消息高于AODV、EG-RAODV的原因。幸运的是，EG-RAODV并不受此影响，原因就在于EG-RAODV利用EEGM模型建立最可靠的路由。

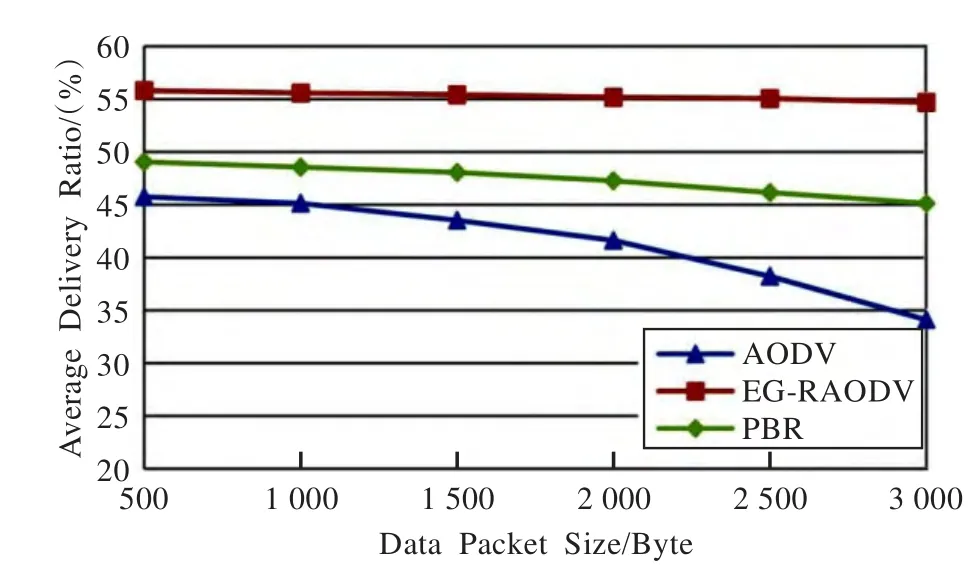
图7 实验B：分组传输率随数据包大小的变化

图8 实验B：分组传输率随路由请求消息率的变化

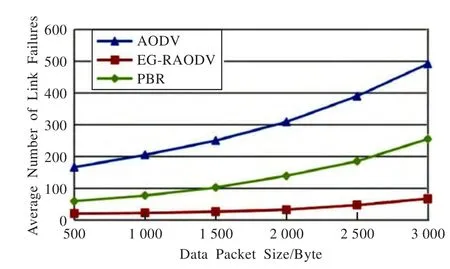
图9 实验B：平均链路断裂数随数据包大小的变化

图10 实验B：平均端到端传输时延随数据包大小的变化

图9显示三个协议的平均链路断裂数的变化情况。从图可知，AODV具有最高的链路断裂数，这也恰好解释了AODV具有最低的分组传输率，如图7所示。由于EG-RAODV选择最可靠的路由，EG-RAODV的路由持续时间长，链路断裂数目少。由于PBR采用链路预测机制，PBR的平均链路断裂数低于AODV。然而，由于PBR只是采取了简单的预测链路寿命机制，无法建立最可靠的路由，PBR的平均链路断裂数高于EG-RAODV。

在实验B中，与PBR和AODV相比，EG-RAODV方案具有最低的平均端到端时延，如图10所示。随着数据包大小的变化，EG-RAODV变化相对稳定，几乎不受影响。PBR以及AODV随着数据包尺寸的增加，端到端时延也随之增长，这是因为数据包尺寸的增大引起分散的数据包增加，任何一个分散数据包传输的失败，就意味数据包的传输失败。

8 结论

针对VANETs的路由问题，本文展开了分析。首先扩展了演化图论，并提出了EEGM的模型。同时，结合Dijkstra算法，提出EG-Dijkstra算法，并将此算法引入EEGM，用以寻找最可靠的通路MRJ。最后，从可靠性出发，提出EG-RAODV路由协议。针对高速公路场景进行仿真，并与PBR、AODV进行比较。结果表明提出的EG-RAODV在路由请求消息率、平均端到端传输时延、链路断裂数以及分组传输率方面均比PBR、AODV高。这主要是因为EG-RAODV通过EEGM模型，计算所有通路的可靠值，并从中选用最可靠的数据通路作为数据的路由；同时，EG-RAODV中转发节点不广播RREQ，只是定向传播，节省了更多网络资源。

[1]Nekovee M.Sensor networks on the road：the promises and challenges of vehicular Ad hoc networks and vehicular grids[C]//Proceedings of Workshop Ubiquitous Comput e-Res，Edinburgh，UK，2005.

[2]Moustafa H，Zhang Y.Vehicular networks techniques，standards and applications[M].New York，NY，USA：Taylor&Francis，2009：7-11.

[3]Abdalla G M T，Abu-Rgheff M A，Senouci S M.Current trends in vehicular Ad hoc networks[C]//Proc of IEEE G lobal Inf Infrastruct Symp，Marrakech，Morocco，2007：1-9.

[4]Blum J J，Eskandarian A，Hoffman L J.Challenges of intervehicle Ad hoc networks[J].IEEE Trans on Intell Transp Syst，2004，5（4）：347-351.

[5]Mao G，Anderson B D O.Graph theoretic models and tools for the analysis of dynamic wireless multihop networks[C]//Proc of IEEE Wireless Commun Netw Conf，2009：1-6.

[6]Monteiro J，Goldman A，Ferreira A.Performance evaluation of dynam ic networks using an evolving graph combina-torial model[C]//Proc of IEEE Int Conf WiMob Comput，Netw Commun，2006：173-180.

[7]Ferreira A.Building a reference combinatorial model for MANETs[J].IEEE Netw Mag，2004，18（5）：24-29.

[8]Jiang S，He D，Rao J.A prediction-based link availability estimation for mobile Ad hoc networks[C]//Proc of IEEE INFOCOM，2001：1745-1752.

[9]Thilagavathe V，Duraiswamy K.Prediction based reliability estimation in MANETs with Weibull nodes[J].Eur J Sci Res，2011，64（2）：325-329.

[10]Taleb T，Ochi M，Jamalipour A，et al.An efficient vehicleheading based routing protocol for VANET networks[C]//Proc of IEEE Wireless Commun Netw Conf，2006：2199-2204.

[11]Feng K T，Hsu C H，Lu T E.Velocity-assisted predictive mobility and location-aware routing protocols for mobile Ad hoc networks[J].IEEE Trans on Veh Technol，2008，57（1）：448-464.

[12]Namboodiri V，Gao L.Prediction-based routing for vehicular ad hoc networks[J].IEEE Trans on Veh Technol，2007，56（4）：2332-2345.

[13]Menouar H，Lenardi M，Filali F.A movement predictionbased routing protocol for vehicle-to-vehicle communications[C]//Proc of 1st Int V 2V Commun Workshop，San Diego，CA，USA，2005：1-7.

[14]M onteiro J.The use of evolving graph combinatorial model in routing protocols for dynamic networks[C]//Proc of XV Concurso Latinoamericano de Tesis de Maestrìa，2008：1-17.

[15]Pallis G，Katsaros D，Dikaiakos M D，et al.On the structure and evolution of vehicular networks[C]//Proc of the 17th IEEE/ACM Annu Meeting Int Symp MASCOTS，2009：1-10.

[16]Ng S C，Zhang W，Zhang Y，et al.Analysis of access and connectivity probabilities in vehicular relay networks[J].IEEE Journal on Selected Areas in Communications（JSAC），2011，29（1）：140-150.

[17]Olariu S，Weigle M C.Vehicular networks from theory to practice[M].New York，NY，USA：Taylor&Francis，2009：344-346.

[18]Rudack M，Meincke M，Jobmann K，et al.On the dynamics of Ad hoc networks for Inter Vehicle Communication（IVC）[C]//Proceedings of the ICWN，Las Vegas，NV，USA，2002.

[19]Kerner B S.Introduction to modern traffic flow theory and control[M].Berlin，Germany：Springer-Verlag，2009.

[20]Niu Z，Yao W，Ni Q，et al.Link reliability model for vehicle Ad hoc networks[C]//Proc of London Commun Symp，London，UK，2006：1-4.

[21]Rudack M，Meincke M，Jobmann K，et al.On traffic dynamical aspects of Inter Vehicle Communications（IVC）[C]//Proc of the IEEE Veh Technol Conf，2003：3368-3372.

[22]Perkins C E，Royer E M.Ad-hoc on-demand distance vector routing[C]//Proc of the 2nd IEEEWMCSA，1999：90-100.

[23]Cormen T H，Leiserson C E，Ronald L R.Introduction to algorithms[M].Cambridge，MA，USA：M IT Press，1990.