一种数据融合B P神经网络的船舶流量预测算法*

刘小东，黄洪琼

（上海海事大学 信息工程学院，上海201306）

近年来，水运总量突飞猛进，造就了我国沿海及长江流域等地的各条“黄金水道”，为我国的经济、社会发展做出了重要贡献。但同时，水运量的增加使水上交通事故频发，造成了巨大的损失，这对水道的设计、规划和船舶通航资源管理的优化配置提出了更高的要求。船舶流量预测的研究为水道的设计、规划和船舶通航管理提供了基础性依据。

[1]提出差分序列特性进行模型的筛选和基于模糊变权重的船舶交通流量组合预测方法实现了船舶流量的预测。参考文献[2]根据组合预测的思想，将三种算法进行智能融合构建一种新的智能预测系统。参考文献[3]利用系统工程的相关原理，提出了基于BP神经网络的数学模型。以上方法各有优缺点，预测精度往往不高，算法稳定性较差。为此，本文提出一种数据融合的BP神经网络预测算法，进一步提高船舶流量的预测精度及算法的稳定性。

1 船舶交通流量预测原理

船舶流量预测指定性预测和定量预测[4]。船舶流量的预测主要受客观环境和算法模型影响，抛开客观因素，算法将是解决预测精度不高的主要因素。船舶流量的预测具有时变、不确定、非线性特征，神经网络模型[5]具有很强的非线性预测能力和泛化能力。本文在选取BP神经网络模型时，引入数据融合机制，其预测原理结构如图1所示。

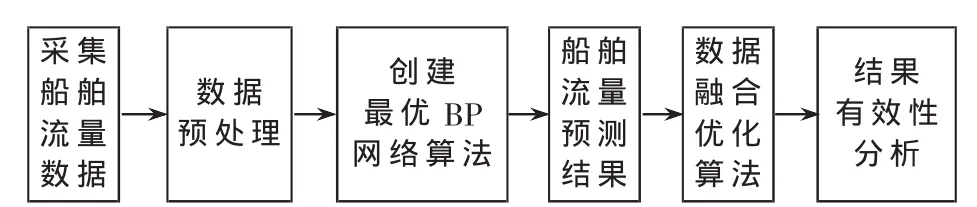
图1 船舶流量预测原理图

2 数据融合BP算法模型

2.1 BP神经网络算法原理

BP神经网络算法[6]的原理是：输入量Xi通过隐含层作用于输出节点，经非线性变换，产生输出量 Yk，网络训练的每个样本包括输入向量和期望输出量，通过调整输入节点与隐层节点的权值Wij和隐层节点与输出节点之间的权值Tjk以及阈值，使网络输出值与期望输出值之间的偏差沿梯度方向下降，经过网络训练，确定最小误差对应的网络参数，训练停止。网络结构如图2所示。

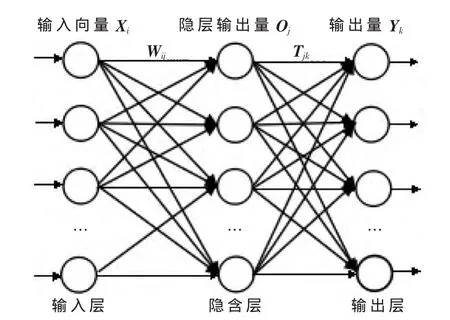
图2 BP神经网络结构模型

2.2 BP算法描述

采集船舶流量VTS数据，预处理成BP神经网络模型训练的样本，然后根据BP神经网络结构建立最佳模型。Xi为输入向量，Oj为隐层输出向量，Yk为输出向量，Wij为第i个输入层到第j个隐含层之间的权值，Tjk为第j个隐含层到第k个输出层之间的权值。

f为非线性神经元函数，θ为神经单元阈值，则：

激励函数是反映下层输入对上层节点刺激脉冲强度的函数，又称刺激函数，一般取(0，1)内连续取值的Sigmoid函数：

误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数,Tpi为节点的期望输出值；Opi为节点计算输出值。

神经网络的学习过程，即连接下层节点和上层节点之间的权重矩阵Wij的设定和误差修正过程。自学习模型中η为学习因子，Фi为输出节点 i的计算误差，Oj为输出节点j的计算输出，a为动量因子，则：

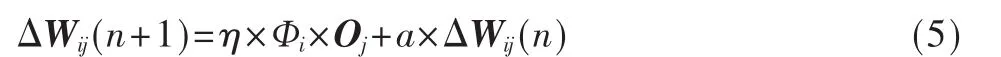
在运用BP神经网络算法时通常方法为归一化处理[7]，将其转换成适合激励函数Sigmoid区间的数据变量，作为神经网络训练的样本。

2.3 数据融合算法

单纯用BP神经网络算法获取的预测值必定存在较大的误差，降低甚至消除这些误差对提高预测精度具有十分重要的意义。通过一种数据融合优化手段，将BP神经网络预测获取的初步预测结果进一步优化，步

(3)构造新的曲线空间。 L(1)，L(2)，L(3)，…，L(n)与平均曲线L(a)作差，记录偏差最大的曲线为L(j1)，L(j2)，…，L(jj)，将其剔除，保留剩下的曲线并重新编号为L(1)，L(2)，…，L(n-j)构成新曲线空间。

(4)新的曲线空间中再次作数据融合加权平均，得到一条较优的预测曲线L：骤如下：

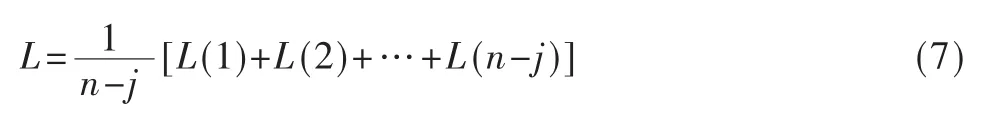
(1)搭建BP神经网络算法模型，进行多次训练获得船舶流量的多条预测曲线 L(1)，L(2)，L(3)，…，L(n)。

(2)将这些曲线进行加权平均得到一条平均曲线L(a)：经过这种多次预测剔除偏差较大曲线的数据融合加权平均处理可以有效地提高预测精度。

(5)获取较优预测曲线 L 中的 k 个值 L1，L2，L3，…，Lk，与期望预测值 T 的 k 个分量 T1，T2，…，Tk作差，取绝对平均值M，如式(8)所示：

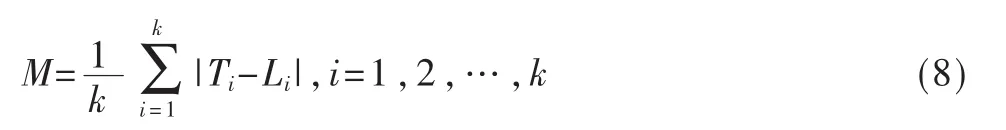
(6)对较优预测曲线L中的k个值依次进行判断，并且剔除偏离门限的点值，利用线性插补法填充剔除的点。

(7)获取平滑系数：其中，Ri表示第i个值的平滑系数，即为平滑的权重；Bi表示Ti与Li的残差Ei所占毛误差E的比例程度：

其中，h为比例程度系数，取10-n，n为正整数，此处n取1。

(8)进行数据的平滑。假设有k个预测值，Li表示第i个预测值，其中，i=1，2，3，…，k。 Hi表示平滑后的最终预测值。

数据融合BP技术[8]预测曲线平滑的过程引入了多次预测并删除误差较大预测曲线及曲线点的数据处理机制，使得算法在预测精度不断提高的同时，有效地提高了系统的容错能力，即使在预测过程中产生了一些误差较大甚至严重偏离船舶交通流量真实曲线的预测值，这些预测值也会在多次预测中剔除异常数据的处理下被删除，较好地降低预测误差的同时提高了船舶交通流量的预测精度，使预测算法具有较好的稳定性。

3 实验结果分析

3.1 预测仿真结果

结合上述算法分析流程，采集宁波港口2012年7月5日～8月 9日船舶流量 VTS数据作为原始数据，预测仿真结果分析如下：

先根据训练好的BP神经网络算法对船舶流量进行预测，预测结果与实际船舶交通流量VTS观测数据对比，如图3所示。

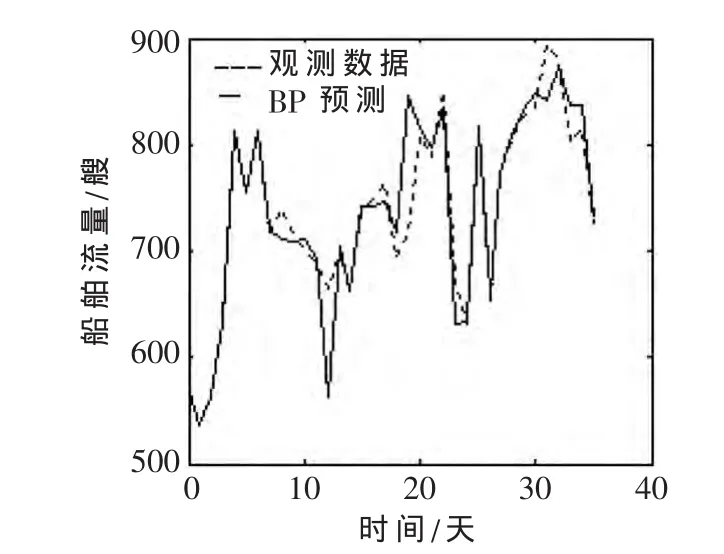
图3 BP算法预测与船舶流量统计

由图3可知，BP神经网络预测算法在整体上虽有一定的预测精度，但部分预测结果偏差较大，预测精度还有待提高，需进一步研究。

数据融合BP神经网络算法在传统BP神经网络算法的基础上引入数据融合思想，用BP神经网络进行100次仿真，将每次预测结果与平均预测结果作差比较，删除一些误差较大的预测结果；然后将剩余的预测结果经过数据加权平均融合获取一条较优的曲线；接着对较优曲线进一步优化，采用数据融合管理机制，以预测结果的残差所占总体误差的大小来设定门限，剔除门限之外的点值，并以线性插补的方法填充剔除点；最后对较优点值进行平滑优化，获得一条高精度的预测曲线。其仿真结果与原始观测数据比较结果如图4所示。

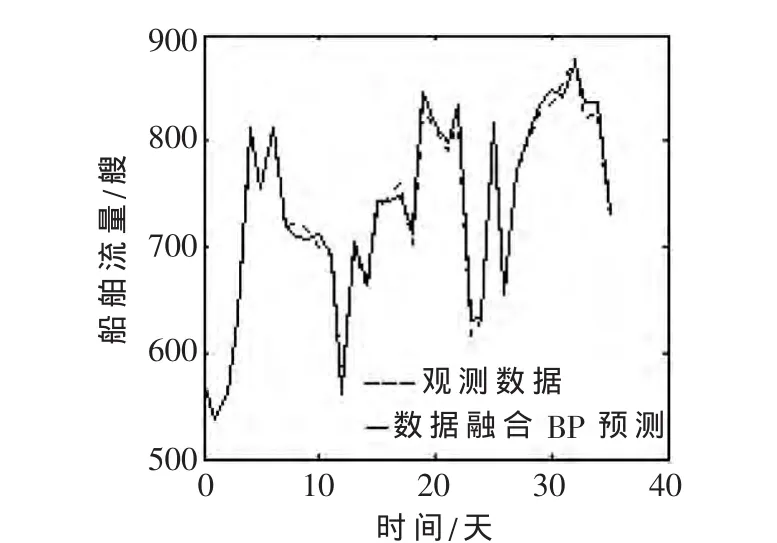
图4 数据融合BP算法预测与船舶流量统计

从图3和图4可以看出，经过数据融合BP神经网络算法的预测结果偏离实际值较小，更接近于船舶交通流量的实际值，预测精度更高，预测效果明显优于传统的BP神经网络预测算法，而且算法稳定性更强。

3.2 算法稳定性及有效性分析

本文在理论分析及实验结果的基础上以算法的方差大小来判断算法的稳定性，以平均绝对误差(MAE)、平均绝对百分误差(MAPE)、均方根误差(RMSE)、均方根误差比(RMSEP)来衡量两种算法的预测精度的有效性。图5为两种算法方差/10的对比图。

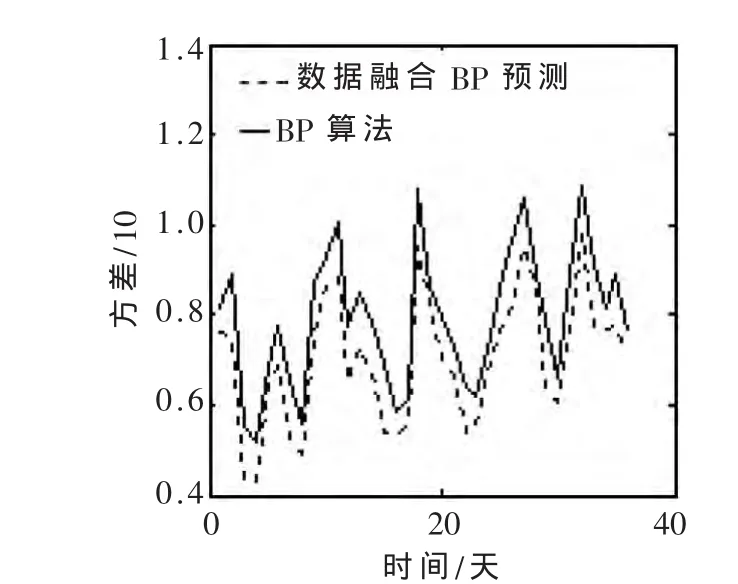
图5 两种算法方差比较图

由图5可知，数据融合BP神经网络算法预测结果的方差明显小于传统的BP神经网络预测算法预测结果的方差，从而说明数据融合BP算法的稳定性更优越。上述数据融合BP预测算法引入了数据融合处理机制，使得算法在预测精度不断提高的同时，有效地提高了算法的抗干扰能力，即使在预测过程中有较大预测误差与测量误差的影响，这些预测值也会在多次估计剔除异常数据的处理下被删除，较好地降低了预测误差对预测精度的影响，使数据融合BP预测算法具有较好的稳定性，从而增强了系统的鲁棒性。

令实际测量值为 Ti，预测值为 Hi，n为观察数据的总数量，预测准确度的指标如下：

平均绝对误差MAE和平均绝对百分误差MAPE分别为：

统计得到宁波港口 2012年7月 5日～8月 9日船舶交通流量VTS总量为26 510艘。传统的BP神经网络预测算法预测的结果为26 415艘，数据融合BP神经网络预测算法预测的结果为26 492艘，两种算法预测精度性能指标比较如表1所示。

表1 两种算法预测性能比较

从表1可以明显看出，数据融合BP预测算法的预测精度各项指标均明显优于传统的BP神经网络预测算法，其预测精度更高，算法稳定性能更强。

经过数据融合的BP神经网络预测算法，在传统BP神经网络预测算法的基础上引入数据融合优化处理机制，有效提高了船舶交通流量的预测精度，合理改善了算法的稳定性，而且智能地调整了数据融合预测权值系数的比例关系。此外，结合门限偏差值的设定剔除偏差较大轨迹点，并进行线性插补剔除的点，最后将曲线值进行平滑处理，获取最优的预测结果。该算法能够较好地实现船舶交通流量的高精度预测，同时有效提高了算法的稳定性，与传统的BP神经网络预测算法相比，其独特的数据融合算法较好地实现了曲线点值偏移量的数据融合优化匹配管理，有效地提高了预测精度，并具有计算复杂度低、稳定性强、适用范围广等优点。

参考文献

[1]杨翔.船舶交通流量预测方法研究[D].大连：大连海事大学，2006.

[2]黄洪琼，汤天浩，金永兴，等.基于智能融合的船舶交通流预测系统[J].中国航海，2008，31(4)：364-367.

[3]王东.基于BP人工神经网络的船舶交通流量预测研究[D].武汉：武汉理工大学，2009.

[4]郎茂祥，傅选义，朱广宇.预测理论与方法[M].北京：北京交通大学出版社，2011.

[5]周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.

[6]蒋良孝，李超群.基于BP神经网络的函数逼近方法及MATLAB 实现[J].微型机与应用，2004，23(1)：52-53.

[7]李晓峰，徐玖平，王荫清，等.BP人工神经网络自适应学习算法的建立及其应用[J].系统工程理论与实践，2004，24(5)：1-8.

[8]吴祖堂.基于神经网络预测器的传感器数据证实技术研究[J].电子技术应用，2001，27(1)：22-25.