畸变进气对两级风扇稳定性影响的数值模拟

王春利，乔渭阳

(1.江西洪都航空工业集团有限责任公司，江西南昌330024；2.西北工业大学动力与能源学院，陕西西安710072)

畸变进气对两级风扇稳定性影响的数值模拟

王春利1，乔渭阳2

(1.江西洪都航空工业集团有限责任公司，江西南昌330024；2.西北工业大学动力与能源学院，陕西西安710072)

基于多级轴流压气机的逐级特性，建立了一种预估多级轴流压气机在均匀进气和周向畸变进气条件下的喘振边界的一维数值模拟方法。根据动态压缩系统模型，对一台两级风扇的喘振边界进行了数值预测，与基于李亚普诺夫理论的线化一维模型和试验结果的比较表明，该模型能较为准确地预估多级轴流压气机的喘振边界。对畸变进气条件下两级风扇稳定性进行的详细数值分析表明：进气总压畸变在流动过程中会生成总温畸变并伴随着总压畸变的衰减，进气总温畸变则会生成总压畸变并伴随着总温畸变的衰减；反向总温总压组合畸变进气时，畸变衰减快稳定裕度损失小，而正向总温总压组合畸变进气时，畸变衰减慢稳定裕度损失大。

航空发动机；轴流压气机；一维模型；畸变；气动稳定性；数值模拟

1 引言

军用航空燃气涡轮发动机在研制和使用过程中，经常遇到失稳引起的发动机压缩系统不稳定工作问题。压缩系统作为航空燃气涡轮发动机的一个重要组成部分，正常工作条件下，为发动机提供合适的质量流量和增压比，最好能保持气动稳定性。然而，实际飞行过程中，特别是进行机动飞行和武器发射操作时，压缩系统通常要受到进口流场波动和其他瞬态变化影响，这些都可能导致风扇/压气机的恶劣工作状态甚至失稳(如旋转失速或喘振)。

由于经济和技术条件的限制，通过试验测试所有气流扰动对压气机的影响不现实，于是人们通过有效的数学模型来获得。鉴于目前三维模型发展得还不够成熟，基于准一维、时间相关模型方程的发动机压缩系统稳定工作理论预测模型，即一维模型，也称stage-by-stage模型，仍具有重要的应用价值。

国外，美国阿诺德工程发展中心的Davis等利用平行压气机理论，采用直接数值求解的时间推进计算方法，对畸变进气条件下的压缩系统稳定性进行了较全面的研究[1～3]。而俄罗斯中央航空研究院，则采用基于李亚普诺夫稳定性理论的计算方法，通过线化控制方程的方法，发展了针对畸变进气条件下的全台发动机稳定性分析程序。本课题组已采用这种方法进行过相关的数值计算[4]。

国内对此也进行了相关研究，但研究得还很不够。有学者基于Davis等发展的stage-by-stage模型，计算了均匀进气和各种畸变进气(包括组合畸变进气)条件下轴流压气机的稳定裕度损失[5，6]，但只比较了不同畸变下的损失大小，并没有分析畸变在压缩系统内部的发展变化和稳定裕度损失机理，且其中文献[6]所用的失稳判据还不太合适。

本文参照Davis等的研究方法，将叶轮机对气流的作用作为源项来考虑，应用时间推进求解初值问题的方法，对航空燃气涡轮发动机的压缩系统进行数值模拟；并利用平行压气机理论，对畸变进气条件下的压缩系统稳定性进行研究。还通过具体算例，深入研究了畸变在压缩系统内部的非定常变化和组合畸变进气下的稳定裕度损失机理。

2 模型方程

如图1(a)所示，发动机空气压缩系统由进气道和多级压气机组成。控制体的建立如图1(b)所示，总控制体由压气机和进出气管道组成，包括气流抽吸影响。其中Fx是轴向力分布，包括叶片和涵道壁面对气流的作用力。外部对控制体提供的能量包括传入的热量Q和轴功SW，从控制体抽吸的气体流量为WB。进气道入口边界条件给定总压和总温，出口边界条件可给定静压、流量或出口马赫数。为更准确地体现压缩系统对气流的作用，总控制体被划分为一系列单元控制体，如图1(c)所示。在压气机区域，一个小控制体包括一级静子和转子。进气道和排气管道同样被分为一些小控制体。图中还示出了单元控制体上的进出口参数。

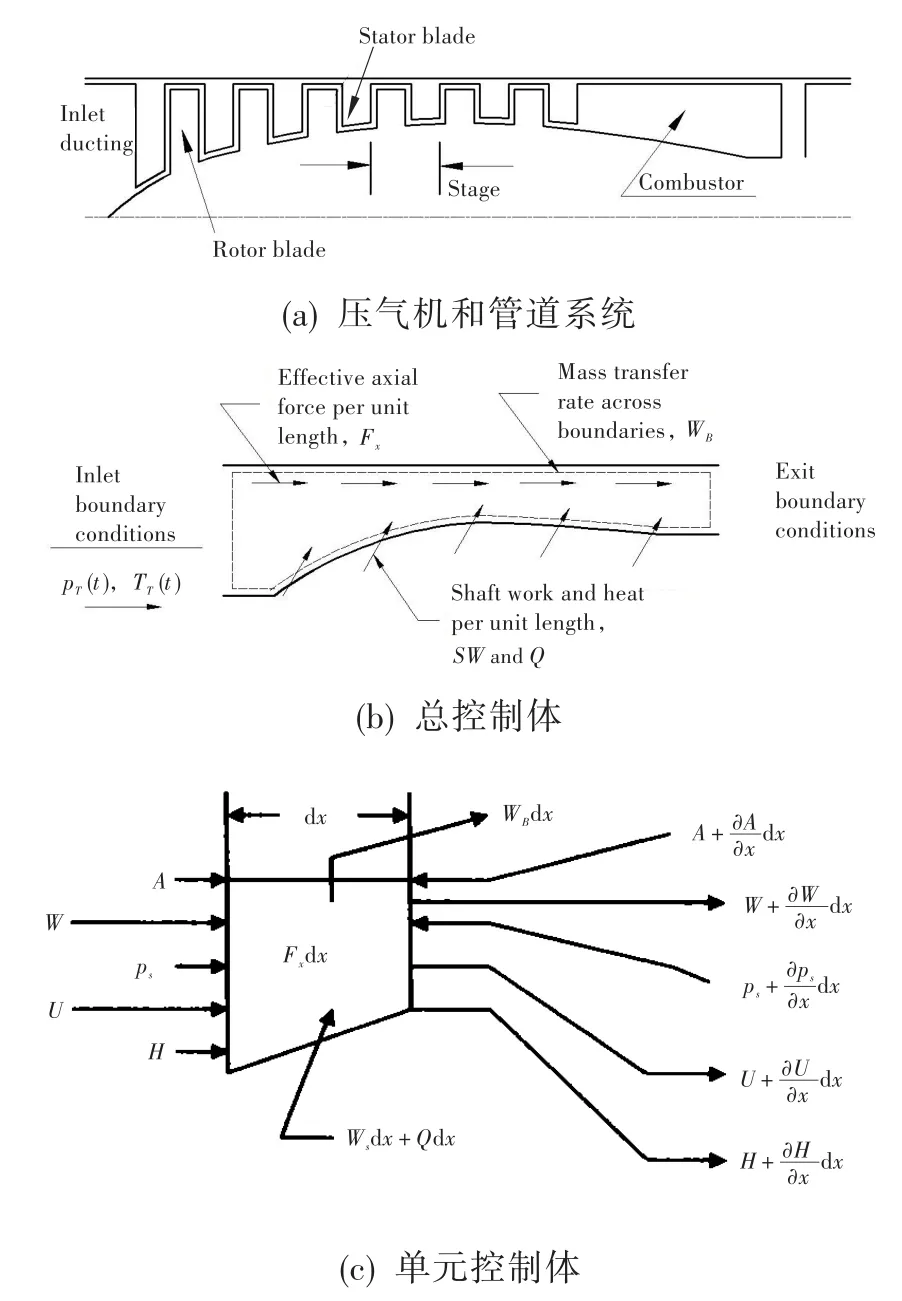
图1 压缩系统物理模型和控制体概念Fig.1 Physical compression system model and control volume concepts

对每个单元控制体应用质量、动量和能量守恒定律，得到控制方程组。连续方程、动量方程和能量方程依次为：

式中：ρ为气体密度，A为控制体截面积，W为质量流率，IMP=Wu+psA为冲量函数，为叶片和机匣环壁面对气流的轴向作用力，E为气体单位体积的内能，H为气体总焓，HB为抽吸部分的热焓。

对于轴向力、轴功等动量和能量方程中的源项，由压气机的准稳态级特性确定。级特性可由试验数据直接取得或采用级叠加法计算获得，本文算例中采用计算获得[7]。对于无叶通道，方程组中的力和功分别表示为：

对于逐级叶片通道，力和功可分别表示为：

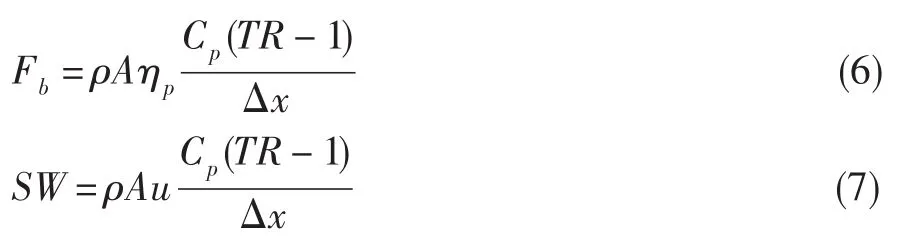
式中：f为摩擦系数，D为水力直径，ηp为绝热效率，TR为总温比。

3 计算方法

守恒型控制方程组的有限差分形式可表示为：

对上述气动方程组，采用二阶精度的MacCor⁃mack预估-校正显式差分格式求解。计算过程中应满足CFL条件，即：

因为本模型既是一个初值问题也是一个边值问题，边界条件处理不当会给数值求解带来麻烦，所以采用特征分析法处理边界条件。在进口应用特征线差分格式，内部控制体用MacCormack格式；出口边界在非堵塞流动情况下用特征线法，在堵塞流动情况下用等熵喷管边界条件。

将进出口段控制体取为等截面管道，若不考虑摩擦和热交换，根据一维非定常欧拉气动方程组和相容性关系，可给出特征方程和相容性方程：

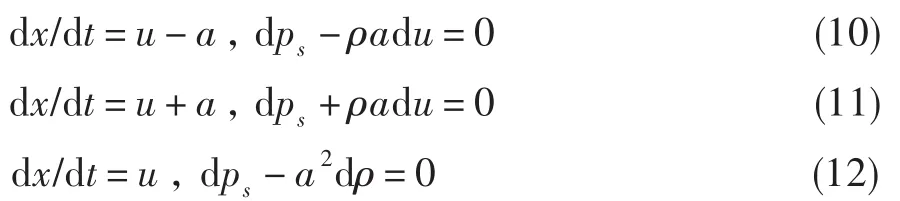
当流动为亚声速时，入口给定总压p*和总温T*，其他参数辅之特征、相容性方程求解；出口截面可给定静压p，再加上特征、相容性方程求解。

本研究发展的计算进气畸变对发动机稳定性影响的程序，使用了经典的平行压气机理论模型[8]。

失稳判断：利用这种动态压缩系统模型的特性，根据文献[1]中方法进行逼喘，给定压气机出口静压升。计算时，为使预测结果足够精确，静压的时间变化率应充分慢。

4 算例分析

为检验所建模型的实际应用效果，对文献[9]中的一台两级风扇进行数值计算。其压缩系统划分为风扇进气管道(划分为三个控制体)、两个风扇级控制体和一个风扇排气管道控制体。

4.1 均匀进气下的程序验证

为考核本文方法、计算程序的可靠性和合理性，首先在均匀进气时，将本模型计算结果与基于李亚普诺夫稳定性理论的线化模型[4]结果和试验数据进行比较，结果如图2所示。可见，在50%～100%换算转速范围内，两个模型所得的特性线和稳定边界与试验结果都相当接近，其中线化模型预测结果偏于保守。故可认为，本研究所用的级特性计算方法和稳定性判别方法可行。

图2 计算模型的试验验证Fig.2 Model validation with experimental results

4.2 进气总压畸变和总温畸变下的分析

算例中研究畸变进气时将风扇分为两个相等的180°扇形子区，总压畸变区为低压区，总温畸变区为高温区。

图3为进口总压畸变度和总温畸变度都为3%时的喘振边界比较。可见，相同畸变度下，总温畸变比总压畸变对压缩系统的影响更大，稳定裕度的减小也更明显，这与文献[1]、[5]的结果一致。

图4示出了100%换算转速下3%进气压力畸变时风扇内总温和总压的非定常变化过程。可见，从0.10 s开始进口给定总压畸变，到0.15 s时流动重新趋于稳定，显然这一过程中叶栅通道内生成了总温畸变，并伴随着总压畸变在下游的大幅衰减。计算数据还表明，总压畸变的高压区是生成总温畸变的低温区，低压区是高温区。图5为不同转速下总温生成和总压衰减的快慢对比分析。可见，进口总压畸变时，风扇转速对畸变的影响不是很大。

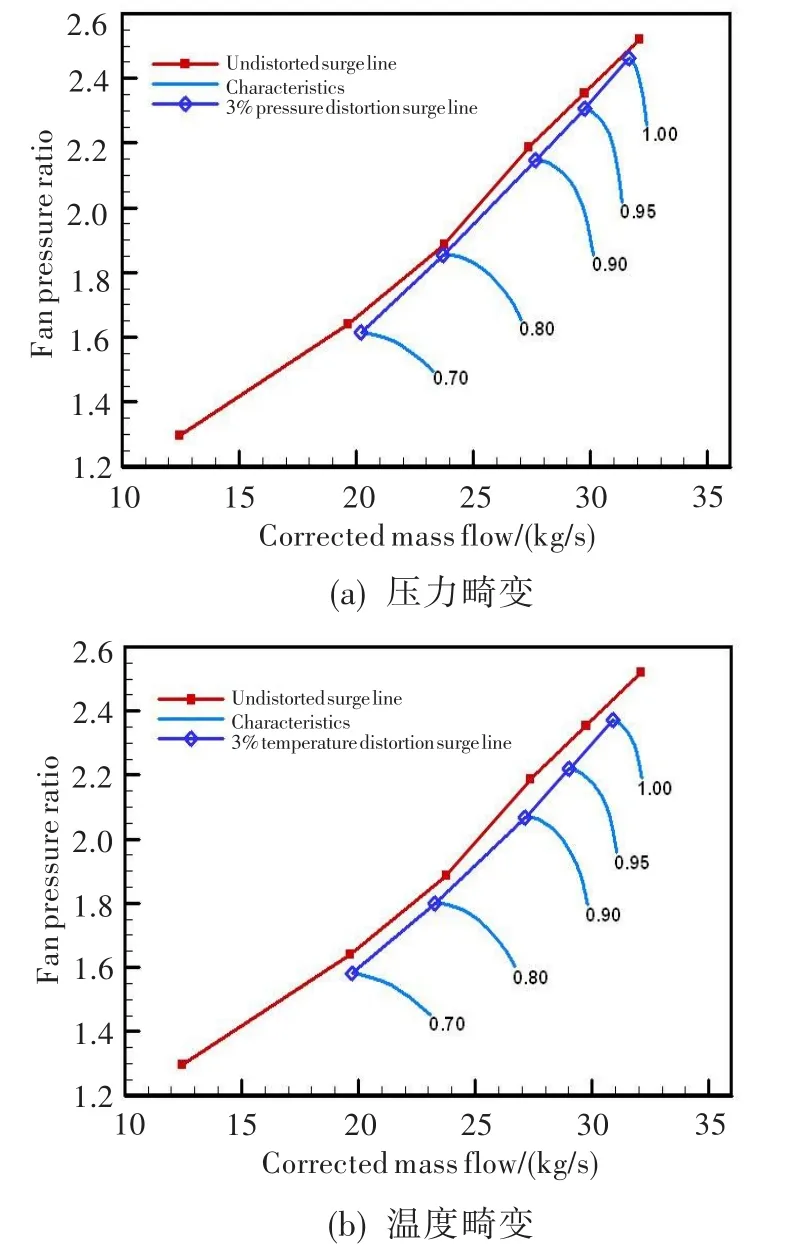
图3 压力畸变和温度畸变下的稳定边界比较Fig.3 Comparison of the stability limit between pressure and temperature distortion

图4 进口总压畸变条件下的温度和压力非稳态图谱Fig.4 The unsteady process after inlet total pressure distortion

图5不同发动机转速条件下进口总压畸变产生的下游压力和温度畸变比较Fig.5 Comparison of the distortion index with inlet pressure distortion under different speeds

图6示出了100%换算转速下3%进气温度畸变时风扇内总温和总压的非定常变化过程。可见，从0.10 s开始进口给定总压畸变，到0.15 s时流动重新趋于稳定，很明显这一过程中叶栅通道内生成了总压畸变，并伴随着总温畸变在下游的衰减。这里也要指出，总温畸变的高温区是生成总压畸变的低压区，低温区是高压区。图7为不同转速下总压生成和总温衰减的快慢对比分析。可见，进口总温畸变时风扇转速越高，总温畸变衰减越快，而总压畸变生成就越慢。

图8示出了三种不同大小进口压力畸变所生成温度畸变的比较。可见，总压畸变越大，生成的总温畸变越大；随着总压畸变的增大，所产生的总温畸变也成比例增大，两者间似乎存在定量关联关系。

4.3 组合畸变下的分析

以对进气单独总压畸变和单独总温畸变的分析为基础，研究进口总压总温组合畸变对两级风扇的影响。图9为反向组合畸变(压力温度畸变处于两个不同的子区间)和正向组合畸变(压力温度畸变处于两个相同的子区间)时稳定裕度下降对比，其中总温畸变和总压畸变的强度都是3%。可见，反向组合畸变对系统稳定性的影响很小，正向组合畸变稳定裕度的损失比反向组合畸变的大得多，这与文献[1]、[5]、[6]的结果相符。若与前文的进口总压和进口总温畸变一起比较，则反向组合畸变引起的损失最小，正向组合畸变引起的损失最大。这可理解为，由总压畸变生成的总温畸变，低压区是高温区，高压区是低温区；与之对应，由总温畸变引起的总压畸变，高温区为低压区，低温区为高压区。如图10所示，反向组合时由于这种生成畸变抵消的影响，压力、温度畸变都衰减得特别快，快于进口单项总压或总温畸变；而正向组合时生成畸变有加强作用，所以两种畸变都衰减得格外慢，慢于进口单项总压或总温畸变。这就解释了为什么反向组合时稳定裕度损失最小、正向组合时损失最大。

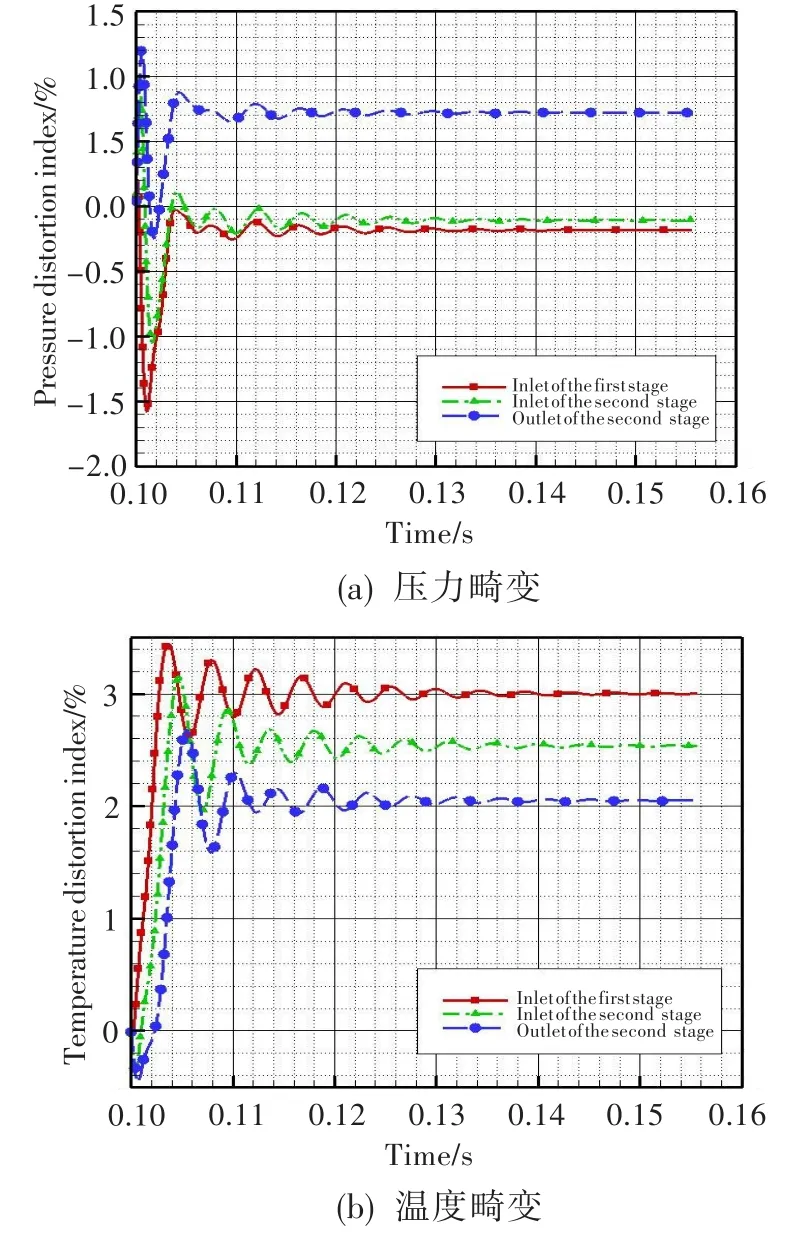
图6 进口总温畸变条件下的温度和压力非稳态图谱Fig.6 The unsteady process after inlet total temperature distortion

图7 不同发动机转速条件下进口总温畸变产生的下游压力和温度畸变比较Fig.7 Comparison of the distortion index with inlet temperature distortion under different speeds

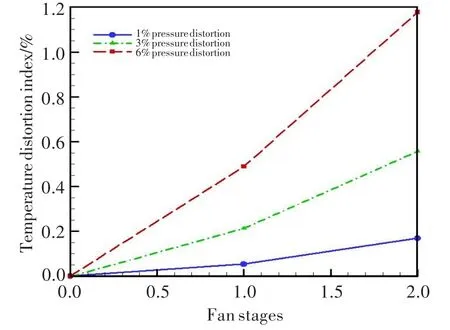
图8 不同进口总压畸变产生的下游温度畸变Fig.8 Temperature distortion produced by different inlet pressure distortion intensity

图9 反向总压总温畸变和正向总压总温畸变下的稳定边界比较Fig.9 Comparison of the stability limit between opposing and overlap combined distortion

图10 反向总压总温畸变和重叠总压总温畸变产生的下游压力和温度畸变Fig.10 Comparison of the distortion index between opposing and overlap combined distortion

5 结论

(1)通过与试验数据和基于李亚普诺夫理论线化模型的比较，验证了所建立的用于分析多级轴流压气机瞬态性能及稳定性的逐级预测模型的可靠性。

(2)进口总压畸变时，在气流流动过程中会生成总温畸变，且生成畸变的高温区在总压畸变的低压区，低温区在总压畸变的高压区；与之对应，进口总温畸变同样会生成总压畸变，且生成畸变的高压区在总温畸变的低温区，低压区在总温畸变的高温区。

(3)进气总压畸变条件下，风扇转速对畸变的生成和衰减影响不是很大，随着总压畸变强度的增大，生成的总温畸变成比例增大；进口总温畸变条件下，转速的影响更明显，转速越高，生成压力畸变越慢，温度畸变衰减就越快。

(4)反向组合畸变时由于生成畸变抵消的影响，压力、温度畸变都衰减得非常快；与之相反，正向组合畸变时生成畸变有加强作用，所以两种畸变都衰减得特别慢。这解释了反向组合时稳定裕度损失最小、正向组合时损失最大的原因。

(5)研究畸变在压缩系统内部的发展变化，有助于理解和预测各种畸变进气条件下稳定裕度的损失。

[1]Hale A A，Davis Jr M W.DYNamic Turbine Engine Com⁃pressor Code:DYNTECC-TheoryandCapabilities[R].AIAA 92-3190，1992.

[2]Gorrell S E，Davis Jr M W.Application of a Dynamic Com⁃pression System Model to a Low-Aspect Ratio Fan:Casing Treatment and Distortion[R].AIAA 93-1871，1993.

[3]Shahrokhi K A，Davis Jr M W.Application of a Modified Dynamic Compression System Model to a Low-Aspect Ra⁃tio Fan:Effects and Inlet Distortion[R].AIAA 95-0301，1995.

[4]乔渭阳，蔡元虎，陈玉春，等.进气畸变对压缩系统稳定性影响的数值模拟[J].推进技术，2001，22(4)：307—310.

[5]吴虎，廉小纯，陈辅群，等.畸变进气下压缩系统稳定性分析的通用方法[J].推进技术，1997，18(5)：62—64.

[6]董金钟，王苗苗.总温总压组合畸变对压气机稳定性影响的数值模拟研究[J].航空动力学报，2003，18(6)：788—793.

[7]Steinke R J.A Computer Code for Predicting Multi-Stage Axial-Flow Compressor Performance by a Meanline Stage Stacking Method[R].NASA TP-2020，1982.

[8]刘大响，叶培梁，胡骏，等.航空燃气涡扇发动机稳定性设计与评定技术[M].北京：航空工业出版社，2004.

[9]Urasek D C，Gorrell E T，Cunnan W S.Performance of Two-Stage Fan Having Low-Aspect Ratio First-Stage Ro⁃tor Blading[R].NASA TP-1493，1979.

Numerical Simulation of Influence by Inlet Distortion on Aerodynamic Stability in a Two Stage Fan

WANG Chun-li1，QIAO Wei-yang2
(1.Jiangxi Hongdu Aviation Industry Group Corporation Limited，Nanchang 330024，China；2.School of Power and Energy，Northwestern Polytechnical University，Xi’an 710072，China)

A quasi one-dimensional,stage-by-stage axial compression system mathematical model for sim⁃ulating surge line with clean or distortion inlet flow has been constructed based on compressor stage charac⁃teristics.The surge margin of a two stage fan was predicted by simulation according to the dynamic compres⁃sion system model.Compared with the experimental data and the linear model based on Liapunov’s theory, it is apparent that this model can predict the axial flow compressor’s stability margin correctly.According to the detailed numerical results for the stability of the two stage fan,inlet total pressure distortion will lead to the generation of total temperature distortion and decrease in the flowage,inlet total temperature distor⁃tion will cause total pressure distortion generation and reduce at the same time.Further more,inlet oppos⁃ing combined distortion of pressure and temperature cause drastic distortion decrease and moderate stabili⁃ty margin loss,while inlet overlaped combined distortion of pressure and temperature cause comparatively moderate distortion decrease and drastic stability margin loss.

aero-engine；axial flow compressor；stage-by-stage model；distortion；aerodynamic stability；numerical simulation

V231.3

：A

：1672-2620(2014)04-0001-06

2013-11-29；

：2014-07-28

王春利(1982-)，男，湖北红安人，工程师，硕士，研究方向为推进系统气动热力学。