电弧触发器稳态温度场计算及其优化设计

蒋心怡，姚高飞，庄劲武



电弧触发器稳态温度场计算及其优化设计

蒋心怡，姚高飞，庄劲武

(海军工程大学电气工程学院，武汉 430033)

为了计算电弧触发器稳态温升，本文建立了电弧触发器二维稳态温度场模型，采用matlab自编程方法计算电弧触发器稳态温度场，并通过温升实验验证模型的正确性。针对圆孔型电弧触发器，本文通过保持狭颈总截面不变，来保证弧前时间一致，并在此条件下研究不同狭颈数对电弧触发器稳态温升的影响规律，以此对电弧触发器进行优化设计。

电弧触发器 稳态温度场 温升 狭颈数

0 引言

电弧触发器是电弧触发式混合型限流熔断器的关键部件，担任着检测短路电流并及时产生触发信号的任务，其性能直接关系到熔断器的分断速度。电弧触发器的设计要求其在额定通流下温升最小，在短路电流下弧前时间最短，以使得熔断器能够对短路电流快速响应，及时分断。目前，国内对大电流电弧触发器的研究有戴超、陈搏等，戴超[1]通过有限元软件Ansys对圆孔型电弧触发器进行了仿真研究，分别分析了熔体结构对弧前时间和温升的影响，但其优化设计时未进行变量的控制，因此优化方案不够具体；陈搏[2]采用差分法和有限元软件Ansys对矩形孔电弧触发器进行仿真研究，得到了弧前时间一致条件下的熔体结构与电阻的关系。

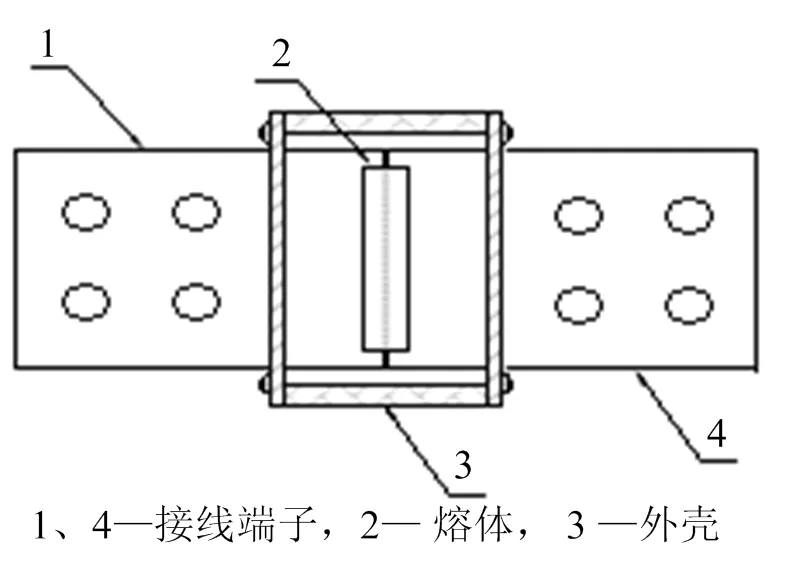
图1 电弧触发器结构

本文建立了圆孔狭颈电弧触发器二维稳态电热耦合场模型，采用matlab自编程方法计算电弧触发器稳态温度场，通过温升实验验证模型的正确性。最后，在弧前时间一致条件下，分析了恒定尺寸熔体狭颈数n与温升的关系，其结果能直接指导工程实践，具有较强的现实意义。

1 电弧触发器建模

1.1物理模型

图2 电弧触发器示意图

1.2 数学模型

稳态情况下，电弧触发器满足电场方程和温度场方程：

1.3边界条件

1）电场边界条件

电流流过的端面满足第一类边界条件，即：

其余边界满足第二类边界条件，即：

2）温度场边界条件

因为触发器银片部分面积很小，且一般被石英砂包裹，石英砂热传导系数很小，因此忽略其对石英砂热传导作用，视为绝热边界，即第二类边界条件：

其余边界皆与空气接触，视为大空间自然对流散热，边界条件为第三类边界条件，即：

式中：，对流换热系数；T，边界面温度；T，远处空气温度。

2 方程离散与计算方法

2.1网格划分

电弧触发器各部分尺寸差别较大，为了减少计算量并保证计算准确性，网格划分采用变网格，银片部分采用小正方形网格（步长0.01 mm），接线端子采用较小正方形网格（步长0.1 mm），大铜排采用大矩形网格（长宽方向步长分别为10 mm、1 mm）。

2.2方程离散

电场方程离散采用中心差分法，温度场方程离散根据单元体热平衡法进行离散。

2.3计算方法

本文采用matlab自编程完成稳态场计算。计算流程为：先求解各节点的电位及温度迭代方程，再更新物性参数，重复以上过程，当满足计算精度时计算停止。

3 实验验证

为验证稳态模型正确性，本文对银片尺寸为：30 mm*6 mm*0.2 mm，含18个圆孔，圆孔直径为1 mm的触发器进行温升试验。实验采用大电流发生装置作为电源，外接3 m长100 mm×10 mm的铜排，通以恒定电流1200 A，经过约4个小时温度基本稳定，记录结果。

表1 稳态场实验与计算结果对比

从表1可以看出实验与计算一致性较好，证明了模型的正确性。

4 电弧触发器优化设计

电弧触发器两个关键性性能为：a) 短路电流下的弧前时间；b) 额定通流下的温升。在设计时，一般要求在其满足温升的前提下缩短弧前时间，以提高触发器对短路电流的响应速度。本文通过控制弧前时间一致，来研究狭颈数对温升的影响，以此完成对触发器优化设计。

以额定通流1600 A触发器为例，研究狭颈数对温升的影响。大短路电流上升率下，电弧触发器的弧前时间只与熔体狭颈截面积有关。因此，为保证弧前时间的一致，在改变狭颈数目的同时，调整狭颈宽度，以保证银片狭颈总截面积相等。

银片长（电流方向）6 mm，宽30 mm，厚0.2 mm。使用稳态温度场模型对不同狭颈数的触发器进行稳态温升计算，表2为计算结果。

表2 不同狭颈数下的狭颈温升

以狭颈数n为横坐标，以狭颈温升为纵坐标，绘制狭颈温升——狭颈数n关系图。

从图3可以看出，狭颈温升随狭颈数目的增加而减小，在孔数15-25之间减小速度较快，25-32之间基本不变，32之后缓慢减小，因为>32之后，狭颈宽度将小于0.16 mm，加工难度增大且狭颈连接强度下降，可靠性降低，因此狭颈数取25为宜。

5 结论

本文对圆孔型电弧触发器建立二维稳态温升模型，并通过温升实验验证了模型正确性。以该模型为工具，通过保证狭颈总面积不变来控制弧前时间一致，改变狭颈数目，得出了狭颈温升随狭颈数目的增加而减小的规律，并提出了最优狭颈数目。

[1] 戴超, 庄劲武. 舰船低压大电流电弧触发式混合型限流熔断器研究[D]. 武汉: 军工程大学, 2010.

[2] 陈搏, 庄劲武. 高压大电流电弧触发式混合型限流熔断器研究[D]. 武汉: 海军工程大学, 2012.

[3] 戴锅生. 传热学[M]. 北京: 高等教育出版社. 2011

[4] 王晨, 张晓锋, 庄劲武, 等．新型混合式限流断路器设计及其可靠性分析[J]．电力系统自动化．2008, 32(12): 61-67．

[5] Kerstin K, Martin K, Lars K．Integration of fast acting electronic fault current limiters (EFCL) in medium- voltage systems[C]. 17th International Conference on Electricity Distribution. Barcelona: CIRED press, 2003: 1-6.

[6] 余跃听, 徐国顺. 舰船电力系统新型限流保护技术的仿真分析[J]. 低压电器, 2011, 24: 1-5.

[7] Hoshino T, Muta I, Tsukiji H, et al. Recovery time of superconducting non-inductive reactor type fault current limiter[J]. IEEE Trans. on Magnetics, 1996, 32（4）: 2403–2406.

[8] 袁志方, 庄劲武, 王晨, 等. 石英砂对于电磁斥力高速开断器介质恢复特性的影响[J]. 高电压技术, 2014, 40(1): 294-299.

[9] 顾雪晨, 王晨. 直流电力系统短路限流装置研究[J]. 船舶, 2012, 23(3): 60-62.

[10] Petranovic R, Miri M．Modeling of the transient behavior of a resistive type high Tc fault current limiter[J]. IEEE Trans. on Applied Superconductivity, 2003, 13（2）: 2036–2039.

[11] 王季梅．高压交流熔断器及其应用[M]. 北京: 机械工业出版社, 2005: 151.

[12] 陈刚, 江道灼, 吴兆麟. 固态短路限流器的研究与发展[J]. 电力系统自动化．2003, 27（10）: 89-94.

[13] Slade P, Wu L, Stacey J, et al. The utility requirements for a distribution fault current limiter. IEEE Trans on Power Delivery, 1992, 7(2): 507-515.

[14] 陈博, 庄劲武, 肖翼洋, 等. 10 kV/2 kA混合型限流熔断器用电弧触发器的分析与设计[J]. 高电压技术, 2012, 38(8): 1948-1955.

Optimization Design and Calculation on Steady-state Temperature Field of Arc Trigger

Jiang Xinyi, Yao Gaofei, Zhuang Jinwu

(Naval University of Engineering College of Electrical Engineering, Wuhan 430033, China)

TM563

A

1003-4862（2014）08-0028-03

2014-06-06

蒋心怡（1960-），女，副教授。研究方向：电力系统安全运行。