SCMDFC算法研究与应用

赵双柱

（兰州文理学院电子信息工程学院 甘肃 730000）

0 引言

DBSCAN算法[1]是聚类分析中最经典的基于密度的聚类分析算法，但算法存在一些问题：聚类质量对参数敏感；不能处理多密度数据集。针对DBSCAN缺点，学者们提出了改进算法，如GDBSCAN算法[2]，KNNCLUST算法，这些算法在执行过程中不能获得任何关于数据项的类属信息，因而通常被看作是一种无监督学习。

1 半监督聚类算法SCMD

1.1 SCMD 算法概述

半监督聚类算法SCMD[3]是Yangqiang Yu等人针对多密度数据集提出的。算法中的先验信息以成对约束（must-link 和cannot-link）形式给出。算法中涉及到两个定义：k最近邻距离和k最近邻列表，分别用P-Kdistance和P-Kneighbor表示。

SCMD算法主要包括三部分内容：首先根据must-link集计算出参考Eps列表；然后根据cannot-link条件从参考Eps列表中选择不同密度分布的代表Eps；最后，以这些代表Eps为参数的多阶段DBSCAN算法运行于数据集，得到最终聚类结果。

1.2 SCMD算法存在的缺点

SCMD算法在一些数据集上确实有着良好的性能，但是仍存在两个问题。

（1）先验约束不充分时不能检测到所有的簇

SCMD 算法在聚类过程中用到的所有Eps都是从must-link约束中计算而来，所以，如果有一个簇不包含must-link约束，则这个簇可能不会出现在最终的聚类结果中。尤其是当这个不包含must-link约束的簇是数据集中最稀疏的簇的时候，它一定会被丢失，而簇中的所有点被分配成噪声。而实际情况是，专家或者用户并不总能提供出数据集中所有簇的must-link约束。

（2）不能处理簇内多密度数据集

SCMD算法不能处理簇内密度不均的情况。而实际存在的数据集合中，簇中间密集而边缘稀疏的情况又是很常见的，这也是一种多密度表现形式。对于簇之间密度不同的数据集，SCMD 算法有良好的性能，因为它能够计算不同密度的不同Eps。而同理，对于一个密度不均的簇，用SCMD 算法可以得到两个或多个Eps，这样这个簇会被分割成几个小的子簇。

2 基于极少约束的多密度半监督聚类算法SCMDFC

2.1 算法主要思想

针对SCMD算法的不足，本文提出了一种改进的半监督聚类算法SCMDFC。该算法的主要思想是：在原算法的基础上添加对这两种问题的处理；问题一的解决方法是：充分利用给定的先验知识，从约束条件集合中挖掘与可能会被丢失的簇的相关信息，从中提取其密度信息，从而查找出所有的簇。问题二的解决方法是：簇内密度不均匀时，该簇会被聚为多个子簇，但在这些子簇中，有一个较大的簇是原来簇的主体部分，通过一定的再分配准则将周围的小的子簇合并到较大的簇中，从而获得自然的簇结构。

2.2 算法详细描述

具体来说，SCMDFC算法主要增添了两种方法来弥补SCMD 算法的不足。

（1）查找可能会丢失的簇，添加Eps

由 SCMD算法可知，如果一个簇中不包含有提供的must-link约束，则这个簇可能不会出现在聚类结果中，因为它的Eps没有被计算出来。所以本文试图添加它的Eps到参考Eps列表中来解决这个问题，关键是如何查找这样的簇。这里，假定这个簇虽然不包含must-link约束，但是包含cannot-link约束中的点。根据约束的传递性，（A，B）属于must-link 集表明数据点A和B属于同一个簇，（B，C）也是一样，我们可以得出数据点A和C属于同一个簇。属于cannot-link集，表明数据点A和B不可能在同一个簇中。如果（A，C）是一个must-link 约束，则数据点B和C也不可能在同一个簇中，我们可以从约束集合中得到传递闭包，则只包含一个数据点P的闭包就属于在聚类结果中可能会被丢失的簇，也就是SCMDFC算法要检测的簇。然后，把P-Kdistance定义为该簇相应的Eps，并将其加入到参考Eps列表中，这样，簇结构将不会丢失。

（2）分配边界簇，解决簇内多密度问题

定义1：（边界簇）一个簇C中的数据点数目小于K时，这个簇是边界簇。即，|C|< K。

为什么簇内数据点数目小于k的簇就是边界簇呢？它不一定就位于某个较大的簇的边界，也许它是远离其他簇的一个独立的簇呢？本算法中是不可能出现这种情况。一个簇必然含有一个或多个核心点，因为簇是由核心点根据直接密度可达的规则扩展来的。核心点的Eps邻域内至少含有M inpts（本算法中是 k）个数据点。如果该簇是一个独立的簇，则它的核心点不可能有k个邻居，因为簇中数据点的总数目小于k。所以该簇中没有核心点。反证证得簇成员数目小于k的簇不是一个独立的簇，而是位于某个较大的簇的边界。

边界簇形成的原因是真实世界中的数据集是多密度的，簇的密度不均匀，且通常是中间密度高边界密度低。SCMD 算法的第三步，Eps值按升序排序，当较小的Eps作为参数用于扩展簇时，某个簇中间绝大多数点被分配为同一个簇标签，而周围的点分配为噪声。当较大的Eps作为参数用于扩展簇时，之前被分配为噪声的一个或多边界点变成核心点开始进行簇扩展，但这些要扩展的点之前已经被标记，所以就形成了成员数目小于k的边界簇。

边界簇就是 SCMDFC算法所要查找的需要再分配的小的子簇。通过定义可以检测边界簇。查找到边界簇后，算法把边界簇分别分配给距离它们相对较近的较大的簇。

2.3 实验结果及分析

下面通过SCMD算法与改进算法SCMDFC的实验对比，来分析SCMDFC算法的优越性。我们选择了两个数据集作为实验数据集，均为多密度数据集，且含有噪声。实验结果中，不同的颜色结合不同的形状代表不同的簇，其中黑色圆点代表噪声。

（1）成对约束（must-link）不充分情况

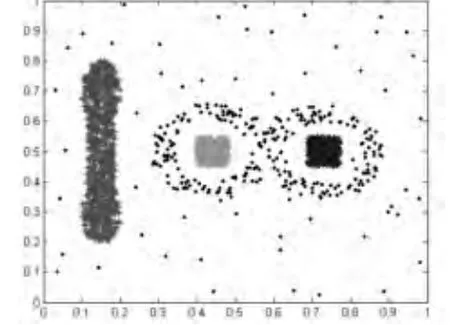
图1 SCMD算法运行于Data1

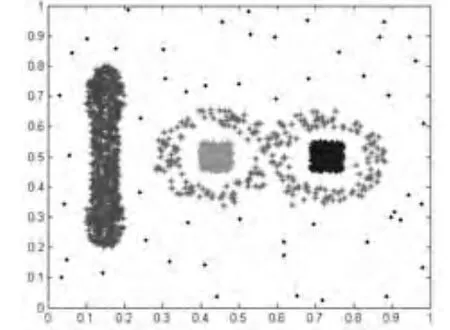
图2 改进的算法运行于Data1

数据集Data1（如图1和图2所示），包含1707 个数据，具有三种密度分布、四个簇结构，且包含噪声。其中两个方形的簇具有相同的密度分布，“∞”形的簇是最稀疏的。设置k=6。如果must-link约束充分，即每种密度分布的簇中都至少包含一个must-link 约束，则SCMD算法和SCMDFC 算法均能有效地发现簇结构。然而，当“∞”形的簇中的must-link约束没有提供时，实验结果显示SCMD算法只能找到三个簇，“∞”形的簇中的数据被分配成了噪声，如图2所示，而算法SCMDFC仍能精确地发现四个簇，如图2所示。

（2）簇内多密度情况

数据集Data2包含1938个数据。该数据集具有三个自然的簇结构且包含噪声，每个簇中的数据都是高斯分布的，也就是说簇中心密度高边缘密度低。设置 K=20，实验结果显示应用SCMD算法聚类三个簇中的大部分点都被正确分配，但簇边界的点被聚成了一些小的簇。改进的算法可以有效地发现三个完整的簇，并正确的识别噪声。

3 结论

本文提出的 SCMDFC算法充分挖掘成对约束集中所包含的信息，在must-link集不充分的条件下，仍能完整查找到所有的簇结构，而且通过一定的再分配准则解决簇内多密度问题，但也存在不足，在must-link和cannot-link约束均不充分的条件下，不能查找到全部的簇结构。在今后的研究工作中，希望能有进一步的改进。

[1]Martin Ester，Hans-Peter Kriegel，JörgSander，et al.A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases w ith Noise[C].In Proceedings of 2nd International Conference on Know ledge Discovery and Data M ining（KDD '96）.1996：226-231.

[2]Jörg Sander， Martin Ester， Hans-Peter Kriegel， et al.Density-Based Clustering in Spatial Databases：The Algorithm GDBSCAN and Its Applications[J].Data M ining and Know ledge Discovery.1998，2（2）：169-194.

[3]Yang-QiangYu，Tian-QiangHuang，Gong-DeGuo，et al.Sem i-supervised clustering algorithm for multi-density and complex shape dataset[C].In Chinese Conference on Pattern Recognition（CCPR '08）.2008：1-6.