故障转子系统轴心轨迹的自动识别研究

刘 刚，李 明，乔宝明，赵利美

（西安科技大学理学院，陕西 西安 710054）

故障转子系统轴心轨迹的自动识别研究

刘 刚，李 明，乔宝明，赵利美

（西安科技大学理学院，陕西 西安 710054）

轴心轨迹是转子系统故障诊断的重要依据，将整周期重采样、归一化的极半径序列引入轴心轨迹自动识别系统。首先对振动信号进行整周期重采样以降低转速和采样频率对小波去噪效果的影响，然后利用小波变换对其去噪并合成提纯的轴心轨迹，最后计算具有平移、伸缩和旋转不变性的极半径序列作为轴心轨迹特征，采用BP神经网络进行识别。实验结果表明该方法具有良好的识别效果。

轴心轨迹；整周期重采样；特征提取；极半径；自动识别

0 引言

轴心轨迹是转子系统状态监测和故障诊断的重要依据，它可以形象、直观地反映设备的运行状态。大量理论和实验研究已经确立了转子系统典型故障模式和其轴心轨迹形状的对应关系，例如不平衡故障的轴心轨迹呈椭圆形，不对中故障的轴心轨迹呈8字形，不对中与不平衡综合故障的轴心轨迹呈香蕉形，油膜涡动故障的轴心轨迹呈内8字形等。传统的方法通过人工来识别轴心轨迹的形状，影响了故障诊断的自动化程度，因此寻求利用计算机自动识别轴心轨迹的方法具有重要意义。

轴心轨迹的自动识别主要有轴心轨迹提纯和特征提取两方面内容。目前轴心轨迹提纯常用方法有形态滤波器[1]和小波变换[2]等，其中小波变换应用较为广泛。特征提取是自动识别过程中的重点，目前主要的方法有：基于图像分块的编码链[3]、不变矩[4-6]和傅里叶描述子[7-9]等，其中后两种方法应用较为广泛。

本文提出一种新的轴心轨迹自动识别方法，将整周期重采样、归一化的轴心轨迹极半径序列引入轴心轨迹自动识别过程，取得了良好的识别效果。

1 轴心轨迹提纯

采用小波变换对两个正交方向上的振动信号进

行去噪，然后将它们合成得到提纯的轴心轨迹。去噪之前先对振动信号进行整周期重采样以降低转速和采样频率对小波去噪效果的影响。实验表明：采用小波变换去噪时对于特定转速和采样频率的振动信号存在一个最佳分解层数，在该层数下小波分解能有效分离有用信号频率成分和噪声频率成分。当转速和采样频率变化时，每个旋转周期上采集的数据长度(数据点数)也发生变化，引起在相同层分解得到的信号频率成分发生变化，采用原分解层数不能有效分离有用信号和噪声信号，需人工重新确定分解层数。经过整周期重采样后，不同转速和采样频率的振动信号在每个旋转周期具有同样的长度，可采用相同的分解层数进行去噪，避免对不同信号人工确定分解层数。下面对基于整周期重采样的小波去噪方法进行描述：

（1）确定每个旋转周期的重采样长度Ne。这里取Ne=64，即重采样频率为旋转频率）。由采样定理，当采样频率大于最高频率的2倍时就可以从采样信号恢复原信号，因此本文重采样后能够恢复的信号的最高频率为达到旋转频率的32倍频。实际故障信号集中在旋转频率的1/2，1，2，3倍频，此频率对于故障分析来说已经足够。

（3）对重采样的信号进行小波阈值去噪。这里采用sym5小波基函数、启发式阈值和软阈值函数进行去噪，经试验确定的最佳分解层数为3层。

下面通过仿真信号来建立几种不同故障的轴心轨迹，并采用前述方法提纯。通过式（1）可获得所需要的轴心轨迹形状，包括椭圆形、外8形、香蕉形、内8形、梅花形5种。

式中：x（t），y（t）——两个正交方向上轴心的位移分量；

s1（t），s2（t）——噪声；

fn——旋转频率；

A1，A2，B1，B2——x（t），y（t）的1、2倍频分量；

α1，α2，β1，β2——相应的初始相位。

通过改变这8个参数，可以获得所需的轴心轨迹图形。图1（a）所示的是5种常见轴心轨迹图形，在两个振动方向上均加入了均值为零、方差0.2的白噪声。图1（b）是提纯后的轴心轨迹，可以看出此方法具有良好提纯的效果。

2 轴心轨迹的特征提取

类似于图形编码链方法中通过一系列编码来体现轨迹特征、傅里叶描述子方法中采用前面若干个傅里叶系数作为轨迹特征，本文首次提出用极半径变化规律（极半径序列）来表示轴心轨迹的特征。

极半径把两个方向的坐标偏移合并起来考虑，体现了轴心轨迹上各点到基点O的距离，见图2中的r。极半径随时间变化，在具体应用时需要对其进行离散化、标准化。本文对极半径进行等时间间隔采样，并作如下规定：

式中：Ne——每个旋转周期的采样长度（这里取整周

期重采样后的长度）；

图1 常见故障的轴心轨迹

r（i）——在第i个采样点的极半径值，是以Ne为周期的函数，即假定极半径在轴心轨迹上旋转一周后回到原位置。

图2 轴心轨迹的极半径

由于监测位置不同、设备参数设置等原因，同一故障实测的轴心轨迹的位置、大小和方向可能不同。为了获得具有平移、尺寸和旋转不变性的极半径序列，进行如下处理：

（1）确定极半径的基点。在不同的基点下极半径会有差别，为消除这种影响，此处选择轨迹的形心作为基点。若在一个旋转周期内的两个方向上的振动信号分别为x（i），y（i），1≤i≤Ne，则形心的坐标分别为

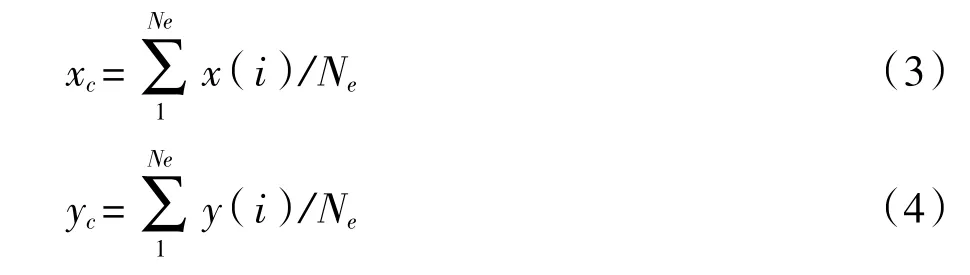
轨迹上的点相对于形心的极半径为

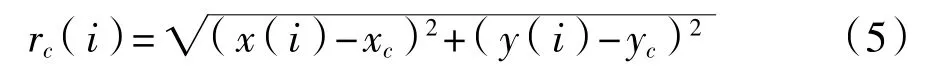
（2）对轴心轨迹大小归一化。对轴心轨迹进行放缩，使其相对于形心的极惯性矩为一常数(这里令这个常数为1）。首先计算出原轨迹相对于形心的极惯性矩：

整个界面布局极接地气，一经推出，深受新生读者的喜爱，“小布”卡通形象深入人心，武汉大学图书馆也借此创立了自己的阅读推广品牌，他们的《基于卡通形象“小布”的高校图书馆阅读推广》获得了2014年度中国图书馆学会“高校阅读推广活动优秀案例”一等奖。

（3）对轴心轨迹旋转归一化。从极半径序列中找出最大极半径（如图2），求出其相对于x轴的夹角θ，然后将轴心轨迹旋转θ角，使最大极半径与x轴重合，以x轴为起点建立新的极半径序列r（i），这样即达到轴心轨迹旋转归一化的目的。

可以证明，经过处理得到的归一化极半径序列具有平移、伸缩和旋转不变性。对前一节所述的几种提纯后的轴心轨迹进行计算，得到归一化的极半径序列变化规律如图3所示。可以看出对于不同的故障，其轴心轨迹极半径序列的变化规律有较大的区别。因此轴心轨迹极半径序列可以反映轴心轨迹的形状特征。归一化的极半径序列长度均为整周期重采样后在每个旋转周期的采样长度Ne=64，便于下一步利用人工智能算法进行分类。

图3 不同轴心轨迹的极半径变化规律

3 轴心轨迹特征识别

采用BP神经网络对轴心轨迹进行特征识别。以每个旋转周期的64个极半径为输入层参数，5种分类作为输出层参数，因此该网络具有64个输入节点，5个输出节点，通过多次试验确定的隐含层节点数为18个。通过改变式（1）中的8个参数，对于图1中的5种轴心轨迹图形各得到20个样本。每种轴心轨迹图形各取18个作为训练样本，将其按照本文提出的方法分别进行整周期重采样、小波去噪、计算归一化的极半径序列，然后输入BP神经网络进行训练。5种轨迹对应的输出向量分别定义为10000（椭圆）、01000（香蕉形）、00100（内8）、00010（外8）、00001（梅花形），训练完成后对网络进行保存。

每种轴心轨迹图形各取两个作为待识别样本（见图4），输入训练好的BP神经网络进行识别，结果如表1所示，其中的数据为识别过程中神经网络的

5个输出端的值。在一次识别中，哪个输出端的数值最接近于1，则这次的识别结果就为该端口所代表的图形。表1最终的识别结果显示用该BP神经网络对图4的仿真图形进行识别时全部正确，体现了良好的识别能力。

表1 轴心轨迹自动识别结果

表2 实测轴心轨迹自动识别结果

4 应用实例

在YE6254转子动力学实验系统上采集转子不平衡、不对中及不平衡与不对中综合故障3类信号各10个样本，部分故障信号的轴心轨迹如图5所示。每类故障信号取8个作为训练样本，对应的输出向量分别定义为100(椭圆)、010（外8）、001（香蕉形），剩下2个作为待识别样本（如图5），识别结果如表2所示。

图4 待识别的轴心轨迹

图5 实测的轴心轨迹

从识别结果来看，6个图形全部正确，说明该方法可以应用于工程实践。表2和表1相比，部分输出向量的最大值并不大，而其他值并不小，有可能发生误识别的情况，这是由于实测的轨迹形状不规则且变化多样引起的。为提高识别准确率，需要采集大量的样本对神经网络进行训练。

5 结束语

噪的自动化水平；归一化的极半径序列具有平移、伸缩和旋转不变性，对于不同的故障其变化规律不同，可以有效地体现轴心轨迹特征；极半径序列的长度固定（为整周期重采样时每个旋转周期的采样长度），便于通过神经网络进行识别，可见该系统各部分是紧密联系的。实验结果表明该系统可有效地识别轴心轨迹，具有工程应用价值。

[1]张文斌，周晓军，李俊生，等.广义形态滤波器在轴心轨迹提纯中的应用[J].浙江大学学报：工学版，2010，44（5）：893-896.

[2]伍卫平，倪国胜，范钦红，等.小波分析法实现水轮发电机轴心轨迹的提纯[J].长江科学院院报，2012，29（1）：53-57.

[3]赵林度，盛昭瀚.离散余弦变换在轴心轨迹自动识别中的应用[J].振动、测试与诊断，1999，19（1）：35-39.

[4]王慧燕，诸静，孙希航.一种改进的基于不变矩的图像匹配算法[J].信息与控制，2003，32（3）：282-284.

[5]陈喜阳，张克危.一种新矩在水电机组轴心轨迹识别中的应用[J].华中科技大学学报：自然科学版，2006，34（3）：79-81.

[6]Boldys J，Flusse J.Extension of moment features’invariance to blur[J].Journal of Mathematical Imaging and Vision，2008，32（3）：227-238.

[7]付波，周建中，陈文清，等.一种基于傅立叶描述子的轴心轨迹自动识别方法[J].电力系统自动化，2004，28（12）：40-44.

[8]王俨剀，廖明夫，吴斌.基于傅立叶描述子自动识别轴心轨迹[J].机械科学与技术，2008，27（6）：799-803.

[9]Avinash B，Tobias H，Wolfram L，et al.Fourier descriptors for defect indication in amultiscaleand multisensor measurement system [J]. Optical Engineering，2011，50（4）：1-10.

式中：V1——列车的控制速度；

Tb——空走时间，约为1～2s；

V2——目标速度；

G——常用制动减速度；

SZ——制动距离，即目标距离。

将表1的参数代入常用制动距离计算公式算出列车的控制速度V1：

经过计算得出：V1=133km/h。

现场实际应用中，在表1的测试数据条件下，厂商的列车控制速度理论设计值为133.5km/h，系统测试结果和理论设计数据基本一致。

表1 系统的测试数据

4 结束语

在高铁列控系统中，应用物联网技术，可能会存在标准和接口不统一、ZigBee无线网络传输速率不够高、RFID的可靠性有待加强[12]、系统扩展不方便等问题，但是随着物联网技术的不断发展，物联网技术会广泛地应用到我国铁路运输领域。本文分析物联网的RFID和ZigBee技术结合其应用现状，设计高铁列车运行控制系统，可满足高铁列控信号技术的教学实验和实训的需求，大大提高高速铁路技术相关专业的教学质量。

参考文献

[1]刘虎兴，范明.中国铁路列控系统现状及发展[J].铁道通信信号，2003，39（2）：1-4.

[2]王晓静，张晋.物联网研究综述[J].辽宁大学学报：自然科学版，2010，37（1）：15-19.

[3]姚仲敏，林大伟.基于物联网低成本智能家居远程测控系统设计[J].电视技术，2012（19）：11-13.

[4]唐涛，郜春海，李开成，等.基于通信的列车运行控制技术发展战略探讨[J].系统仿真学报，2005，18（6）：25-29.

[5]徐丽，张勇.CTCS3级列控系统车载设备仿真子系统的设计与实现[J].铁路计算机应用，2007，17（5）：8-11.

[6]魏学凯.GSM-R在中国列车控制系统CTCS中的应用[J].科技创业月刊，2005（9）：150-151.

[7]Guo Y M，Wang Z W，Wu F，et al.Train operation and movement simulation system[J].Journal of Lanzhou Railway University，2002，21（6）：125-127.

[8]熊向杰，王鲁豫.CTCS地面点式应答器的设计[J].科技信息：学术研究，2007（13）：29-31.

[9]韩胤，张勇.CTCS3级仿真系统中无线闭塞中心的仿真[J].铁路计算机应用，2007（3）：43-45.

[10]张敏，陈春俊，黄海莲.基于物联网的电梯实时监测系统设计[J].中国测试，2012，38（1）：101-105.

[11]郜春海，唐涛，张建明.高速铁路列车运行控制系统车载设备的软件设计[J].北方交通大学学报，1999，23（5）：77-82.

[12]Horste M M，Sehnieder E.Modeling train control system with petri nets-a functional reference architecture[C]∥Proceedings of the IEEE International Conference on Systems Man and Cyberneties，2000：3081-3086.

Automatic identification of orbits of rotor system with faults

LIU Gang，LI Ming，QIAO Bao-ming，ZHAO Li-mei
（School of Science，Xi’an University of Science and Technology，Xi’an 710054，China）

Rotor orbit is an important basis for rotor system fault diagnosis.Full period resampling and normalized polar radius sequence are introduced into the automatic recognition system.Firstly，vibration signalsare processed with full period re-sampling to reduce the influence on the wavelet de-noising effect by rotation speed and sampling frequency.Then，they are de-noised with wavelet transform to synthetic purified orbit.Lastly，normalized polar radius sequence which is invariant to translation，scaling and rotation of the rotor orbit is calculated and used as the orbit feature.Rotor orbits are identified using the BP neural network.Experimental results show that the method has good recognition effect.

rotor orbit；full period re-sampling；feature extraction；polar radius；automatic identification

TM303.3；TP277；TN911.7；TP391.413

：A

：1674-5124（2014）01-0110-05

10.11857/j.issn.1674-5124.2014.01.028

2013-07-14；

：2013-09-01

国家自然科学基金项目（11072190）

刘 刚（1986-），男，四川南充市人，助理工程师，硕士，主要从事工程结构动力学故障分析与控制研究。