社交网络中的社团结构挖掘

范 超，王厚峰

(1. 北京大学 软件与微电子学院，北京 100871； 2. 北京大学 计算语言学教育部重点实验室，北京 100871)

1 引言

随着互联网的蓬勃发展，社交网络在人际交往中发挥着越来越重要的作用。发现其中的社团关系，分析社团的属性，是一项非常有意义的工作。

不少学者从不同角度对社团网络及其属性做了研究，出现了小世界特征[1]、幂律分布[2]和社团结构[3-6]等相关的成果。尤其是社团结构，它在反映同一个团体内成员的行为特征方面，起着非常重要的作用。近年来，不少研究人员都在研究如何发掘社团结构[3]。

“人人网”是国内影响最广泛的虚拟社交网络之一。其前身是“校内网”，用户的主体来自高校在读或已毕业的学生。从中发掘社团结构，有助于分析高校不同群体的一些特点。

除此之外，研究社团结构的挖掘工作还具有其他的一些应用价值和现实意义。一方面，它有助于我们了解社交网络的内在特征与结构；另一方面，它还可以扩展到微博等社会媒体上来，应用于商业领域，例如，针对发掘出的社会团体，投放符合其特征和兴趣的新闻和广告，提供个性化服务。另外，研究社团发掘工作，还能够为其他诸如突发事件的应急处理提供支持。通过研究社交网络中关键社团的发掘，有助于了解重大突发事件在社团内部、以及多个社团之间的传播与扩散机制，甚至能够为相关部门制定预警和防范措施提供一定的帮助。

本文从网络的结构信息和节点的内容信息入手，研究了人人网的社团结构挖掘，并以北京大学的部分用户数据作了实验。主要内容包括： 第一，使用社会网络分析的方法来标注北大用户的院系属性，以此构建评测答案；第二，提出了一个改进的CNM算法，在网络结构信息基础上发掘社团结构；第三，引入节点属性的内容信息，辅助改进社团发掘的效果；第四，对实验结果作了分析，发现社团反映了不同院系和学科的特点。

2 相关工作

社团是这样的一些子群体，内部连接稠密，外部连接稀疏。有两种典型的社团： 团块社团(Clique Communities)和传递社团(Transitive Communities)[6]。社团发掘的典型方法有： 图划分方法、随机块模型方法和基于模块的方法。

图划分方法(Graph Partitioning)是一种传统方法，它通过不断地删除边来分离网络并得到社团。但是，寻找精确的解是一个NP-hard问题[6]。现在，有许多近似算法可以使用，例如，METIS、网络流方法、Kernighan-Lin算法、谱划分方法。METIS采用多级迭代二分和多约束的划分策略[7]；网络流方法则是借助网络流理论中的最大流/最小割的框架来划分社团[8]；Kernighan-Lin算法使用贪心策略，同时最优化社团内与社团间的边数[9]。谱划分多采用迭代二分法，例如，使用最小的两个特征值所对应的特征向量进行社团划分[10]。尽管如此，对于大规模网络来说，图划分的方法仍然未被广泛采用。

随机块模型方法(Stochastic Blockmodeling)是社团发掘的另一种方法。该方法以一定的概率对社团进行划分，划分过程具有不确定性。Nowicki和Snijders提出了一般的随机块模型的方法，使用Gibbs采样来推导位置的后验分布[11]。Wang等人提出了泛化的随机块模型，支持使用属性信息和主题特定的知识[12]。Zhang等人则提出了适用于大规模社会网络的随机社团发现模型[13]。但是，随机块模型的方法引入了概率模型，可能会导致求解过于复杂。

模块性方法(modularity-based method)是广泛使用的一种社团划分法，其核心是模块性Q[4]。该方法最早由Newman在2004年提出，它是一个评价社团结构的利益函数，其值反映整个网络结构的优劣。Q值越高，表明社团内的连接越紧密，并且社团间的连接越稀疏。假设G=(V,E)是一个无向图，|V|=n，|E|=m。G由邻接矩阵表示，Axy是邻接矩阵第x行和第y列上的元素：

节点x的度定义为：kx=ΣyAxy，因此，模块性Q由式(2)计算：

其中，kx为x的度数，Cx代表节点x属于社团Cx。如果x和y在同一个社团内，函数φ(Cx,Cy)为1，否则为0。Pxy是随机情况下x和y之间可能的节点度，已有实验表明，对于网络中较好的社团结构，这个值通常高于0.3[5]。

目前已有多种基于模块性的方法用于发掘社团。Newman最初采用了一种贪心最优化Q的策略[4]；后来，出现了更有效的CNM算法[5]；近来，受到谱聚类理论的启发，Newman采用模块性矩阵的特征向量，来辅助最大化模块性指标[14]。

Danon等人[15]的研究表明，基于模块性的方法优于其他方法。CNM算法作为优秀的模块最大化方法，在准确性和处理效率上都达到了不错的效果。另外，它能够同时利用网络的结构信息和节点的内容信息，本文以CNM算法作为社团结构发掘的基本算法。

3 CNM算法和改进

首先简要地介绍一下CNM算法的原理，然后提出两种改进方案： 引入网络结构信息和引入节点内容信息。

3.1 CNM算法

CNM算法是一个基于模块性Q的层次聚合式聚类算法，通过贪心法最优化Q得到一个社团结构。为了提升算法的效率，Clauset引入了一些高级数据结构[5]，使算法更为有效。算法的要点是采用平衡二叉树和最大堆来减少计算代价，通过自底向上归并。具体步骤如下： (1)所有网络中的节点作为一个单一的社团；(2)对于任意两个社团，计算它们合并后ΔQ的增量，贪心地选择使ΔQ最大的两个社团合并。因为合并会导致每个团体内部的ΔQ发生变化，因此，更新所有与新社团有连接的社团的数据结构信息，再重复上一步的过程；(3)当ΔQ<0时，终止算法。算法的运行复杂度为O(m*d*logn)，其中，d为层次聚类树的深度。Clauset认为在真实的社交网络中，通常有m～n、d～logn[5]，因此，算法复杂度为O(n*log2n)。

3.2 引入网络结构信息改进CNM算法

虽然CNM算法能够非常有效地发掘社团结构，但结果并不十分完美。对于人人网而言，存在很多节点用户是网络的人气节点，连接着许多互不关联的社团(例如，学校的不同院系)，在社团间的交流中起到重要的作用。也就是说，这些节点有着较高的betweenness。所谓betweenness，就是经过某一点Y，连接其他两个点X和Z的最短路径数占二者最短路径总数的比例[16]。这些节点具有控制其他用户交流的能力。Betweenness的概念可以扩展到边上，Givan和Newman提出了一个“边betweenness”的概念[3]，这些边通常是连接着两个社团的关键边，删除这些边可以使不同社团之间的连接边更少。而社团发现的目标就是尽量使社团内的边更多，社团间的边尽量少。引入betweenness的网络结构信息，可以进一步提升传统CNM算法的发现精度。

以下的算法依次删除betweeenness最高的一些边，并把这一过程作为CNM算法的预处理步骤，其过程可简单地表示为：

1) 计算网络中所有边的betweenness；

2) 删除betweenness最高的α条边；

3) 使用CNM算法来发现社团的结构，每次选择使得模块性Q值增大最多的一条边来合并，直到它的增加值小于或等于0，停止合并。

算法描述如下：

输入：删除的边数α，网络图graph

输出：划分的社团clusterSet

ImprovedCNMClusterer clust = initImprovedCNMClusterer(graph);

clust.removeEdges(α);

clusterSet = clust.CNMcluster();

removeEdges(α)函数伪代码：

BetweennessCentrality bc = computeAllBetweennessCentrality(graph);

If α > 0 and α < graph.getEdgeCount()

FOR k=0 to α

toRemove; score = 0;

//find the edge whose betweenness is maximum

FOR e in g.getEdges()

IF bc.getEdgeScore(e) > score

toRemove = e;

score = bc.getEdgeScore(e);

//remove the edge

g.removeEdge(to_remove);

第一步betweenness的计算复杂度为O(mn)；每次删除betweenness最高的边的时间复杂度为O(m)，总的复杂度为O(αm)；第三步CNM算法的计算复杂度为O(m*d*logn)。真实的网络中，有m～n、d～logn，因此，改进算法的复杂度为O(n2)。

3.3 引入节点内容信息改进CNM算法

除了网络本身的结构信息，节点的一些属性反映了它的某些特征。一般而言，具有相同或相似特征的节点应该属于同一社团。具体到人人网的北大用户上，可以通过引入节点的属性信息发现共同院系的两个没有连接的用户。最近，已有学者融合结构和内容信息发掘社团[17-19]，本文使用人人网用户的日志信息，在改进CNM算法方面做了初步尝试。

引入节点内容的基本方法是： 通过用户日志内容，计算任意两个用户之间的相似度，若相似值高于某个阈值β，则将两个用户连在一起，无论原有网络中用户节点是否相连。

为了计算节点间的相似度，首先利用用户节点的属性构造用户模型。这里仅采用日志信息，把每个用户的所有日志合并，再抽取特征，用一个向量来表示用户模型。具体方法是：先分词并标词性，去掉停用词，再抽取其中的名词作为特征，使得每个用户对应一个特征向量di= (wi1,wi2, …,win)；之后，用cosine法计算两个特征向量的相似度。

这里，特征词的权重wij采用标准的tf.idf的计算方法，如式(3)所示。

wij=tfij*idfj=fij* (log2(n/nj)+1)

(3)

其中nj> 0

cosine相似度的计算公式如式(4)所示。

预处理中，计算所有节点对之间的相似度为O(n2)，CNM算法的复杂度为O(m*d*logn)，因此，引入节点内容信息的算法复杂度为O(n2)。

4 实验

4.1 数据采集

本文选择人人网数据进行实验。由于人人网的数据庞大，本文主要采集了北京大学的在校学生用户数据作为实验数据。利用人人网的开放API，可以采集到用户的部分属性信息和所有关系信息，包括： 用户id、用户名、学校、朋友id的集合、用户日志。

采用广度优先策略爬取用户数据。首先，选取北京大学的某个用户作为种子节点，抓取用户信息和好友信息；然后，把好友关系中属于北京大学的用户保留下来，放到待爬取列表中；再通过这些好友，不断地向外抓取，直至所有待爬取列表为空。最终，从人人网获取到的数据量为77 677个，其中有76%的用户来自北京大学。所有用户的好友人数为12 630 015，平均好友为162.6个。其中，好友数量随用户人数的分布关系如图1所示。由于人人网限制了最大好友数量为1 000，所以，除了在1 000的点上有一个暴增之外，基本上是随着好友数量的增加，用户的人数不断减少。

图1 用户人数与好友数量分布统计

同样，再计算所有用户中任意两个用户之间的最短路径(图2)。人人网中的用户距离在6以内，绝大多数是3和2(42.42%用户的距离为3，35.08%用户的距离为2)。当然，在真实的网络中，也可能出现一个北京大学同学认识的某个同学在人人网上并没有加为好友的情况，但从实验结果来看，基本上符合六度分离的原则。

4.2 标准答案的构建和评价方法

在社团挖掘领域，主流的评测方法是采用真实的数据作为评价的标准答案[3-6]。在以大学生为主的人人网上，院系内部的学生之间的关系相对于其他院系，通常会更加紧密。因此，本文采用用户所在的院系这一属性作为划分不同团体的答案。

由于人人网的API限制，用户所在的院系属性无法被获取到。为了解决这一问题，我们从网上找到了北京大学官方发布的09届毕业生名单，名单包含了所有09届本科毕业生的姓名以及所在院系。本文通过如下方法来构建一个09届北京大学本科毕业生的用户网络：

1. 把人人网的用户名预处理成规整的形式。例如，用户“刘少龙 Aspen”处理成“刘少龙”(人人网允许在真实姓名后添加一个后缀)；

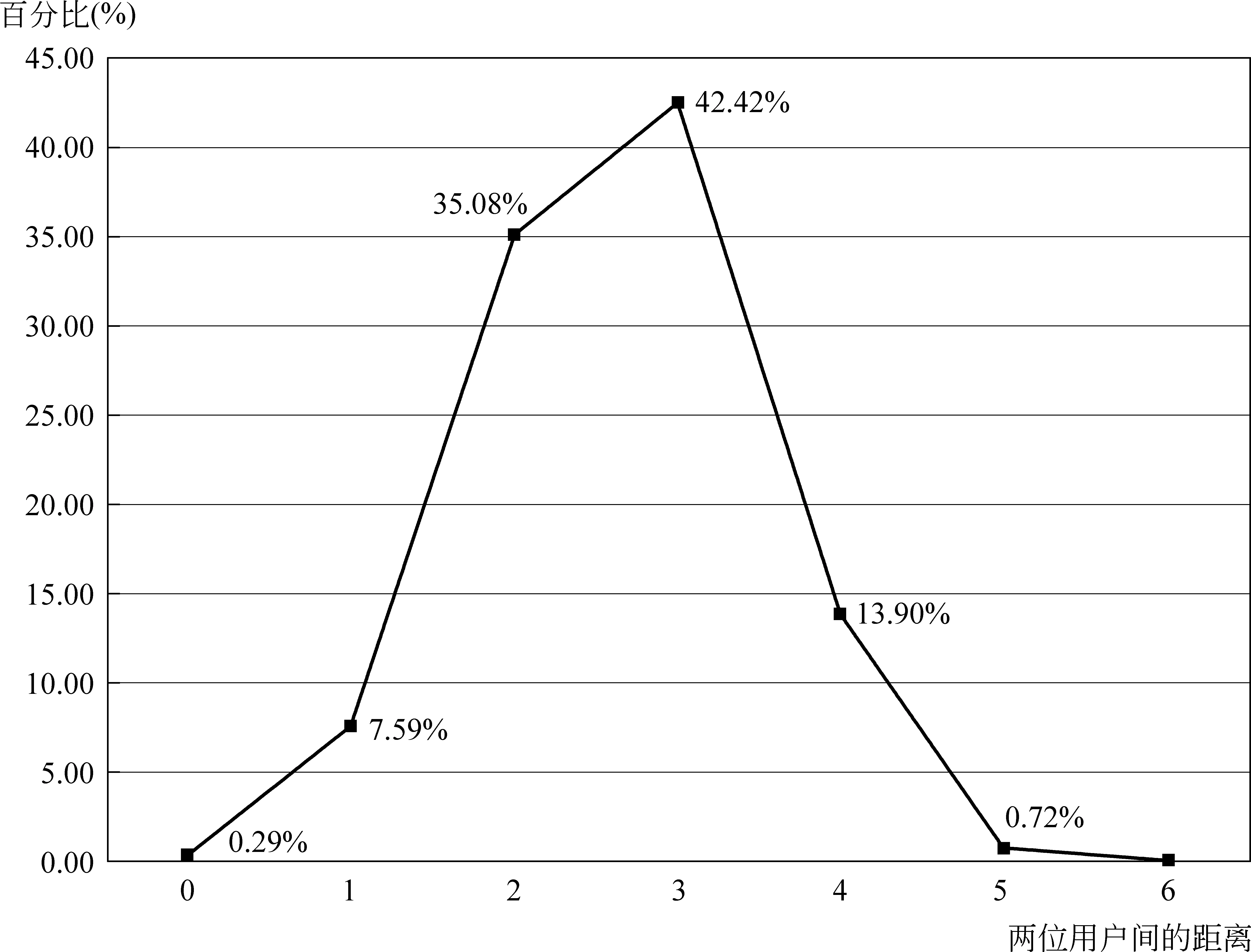
图2 两个用户节点间最短路径的分布

2. 把用户中没有歧义的用户名与毕业生名单进行对比，若名单中含有该名字，则挑选出来并附上其所在的学院放到队列Q中。例如，“鲍重铮”在人人网数据中只有一个，对应到名单中的“数学科学学院”，加入Q；而数据中有多个“王硕”，则推迟处理；

3. 统计重名用户的好友所在的学院，若好友中属于某一学院的人数大于一定个数(初始阶段这个值设定的较高)，我们认定该用户属于相应的学院，并把这些用户加入Q中；

4. 重复步骤3，通过迭代，发现更多的用户及所在学院；

5. 通过人工的方法标记剩余的一些用户。

通过上述过程，从人人网数据中找到了所有3 645名09届本科生中的2 375名，作为本文评测的数据和答案。在这些数据中，只有重名情况存在不确定性，但最后通过人工验证得到的答案也是基本可靠的。值得一提的是，使用社会网络中的好友关系为解决重名问题提供了一种思路。

本文采用聚类度量指标P-IP score[20]来进行评价。P-IP score包括纯度(Purity)、逆纯度(InversePurity)和F值(Fscore)这三个指标。其中，F值为前两个的调和平均数。

5 实验结果和分析

本文进行了多组对比实验，原始的CNM算法作为评价的baseline。同时，我们对社团发现的结果进行一个分析，简单地对北京大学不同院系和学科的特点做了分析解释。

5.1 实验结果

实验结果分三部分： 第一部分在baseline的基础上，引入了网络结构的信息betweenness进行改进；第二部分在baseline的基础上，仅增加了节点的一些内容信息进行改进；第三部分，融合前两部分的结果。

5.1.1 使用网络结构信息改进的结果

表1是在相同数据集上，CNM算法和利用betweenness预处理的改进算法的一个实验结果，括号中是预处理删除betweenness最高的边数的阈值α。Baseline的F值达到了83.96%，取得了一个较好的效果。这一结果也验证了使用院系属性来划分社团是基本有效的，人人网中存在着这么一种社团结构。从结果中还能看到，当删除的边数为21时，F值达到最大88.28%，取得最高的社团发现精度。当不断增加预处理删除的边数时，F值有一个波动。删除过多的边，F值低于CNM算法的水平，这是因为删除过多的边破坏了网络的社团结构，导致了纯度和逆纯度两者都下降。

5.1.2 使用节点内容信息改进的结果

表2是在原CNM算法基础上，仅增加内容信息的结果。括号中的数字表示相似度阈值β，当两个节点之间的内容相似度高于这个值时，会保证在这两个节点间有一条边。结果显示，仅引入内容信息，能有2个多的百分点提升。但如果阈值设置过低，会导致过多的边被引入，甚至增加不同社团之间的连边，反而会降低性能。

表1使用betweenness改进的CNM算法和原始CNM算法的对比

Methods/%PurityInversePurityFscoreBaseline(CNM)89．1879．3283．96ImproCNM(20)89．3081．1785．05ImproCNM(21)90．6186．0688．28ImproCNM(22)87．3782．5684．90ImproCNM(23)89．3580．8884．90ImproCNM(24)88．1780．3784．09ImproCNM(25)90．8283．6287．07ImproCNM(26)90．8679．7884．96ImproCNM(27)89．6875．5782．03ImproCNM(28)89．2282．5685．76ImproCNM(29)90．8677．1783．46ImproCNM(30)91．2475．6682．72ImproCNM(35)87．1672．2178．98

表2使用内容信息改进的CNM算法和原始CNM算法的对比

Methods/%PurityInversePurityFscoreBaseline(CNM)89．1879．3283．96ImproCNM(0．95)90．1979．4184．46ImproCNM(0．9)90．5381．4385．74ImproCNM(0．85)90．3681．3985．64ImproCNM(0．8)89．6082．2785．78ImproCNM(0．75)89．7382．0285．70ImproCNM(0．7)92．0080．7686．01ImproCNM(0．65)85．9885．4385．71ImproCNM(0．6)84．5581．6883．09ImproCNM(0．55)85．7777．8581．62ImproCNM(0．5)86．5777．7381．91ImproCNM(0．45)87．6370．5778．18

5.1.3 使用结构和内容信息改进的结果

原始的CNM算法本质上仅采用了网络的结构信息，因为网络中任意两点之间是否连边来自真实的网络，是确定的。通过融合betweenness的结构信息改进和节点内容的改进，得到如表3的结果，这里取效果最好的一组数据β=0.7。

表3融合两种信息改进的CNM算法和原始CNM算法的对比(β=0.7)

Methods/%PurityInversePurityFscoreBaseline(CNM)89．1879．3283．96ImproCNM(20)90．5780．2985．12ImproCNM(21)88．8976．3782．16ImproCNM(22)92．3077．9884．54ImproCNM(23)89．9486．9188．40ImproCNM(24)90．2881．5285．67ImproCNM(25)91．2985．8988．51ImproCNM(26)90．9176．7683．24ImproCNM(27)91．0481．5686．04ImproCNM(28)90．5379．0384．39ImproCNM(29)90．9581．2285．81ImproCNM(30)92．7679．2485．47ImproCNM(35)89．5274．8281．51

结果表明，融合两种信息的结果会比仅使用结构信息的结果略微好一些。其中，最高F值88.51%仅比表1中的最高值88.28%提高0.23个百分点。这一结果符合Hsu对一般社会网络进行分析的结论： 基于图的关系特征已经足够有效，利用属性特征的效果一般[21]。

最后，三组改进算法与CNM算法的运行时间如表4所示。根据之前的分析，三组改进算法的计算复杂度均为O(n2)，但融合两种信息的算法显然在时间上要大于前两者，而真实社交网络下CNM算法的复杂度大致为O(n*log2n)，实验也论证了其速度明显要快很多。

表4 CNM与三组实验运行时间对比

5.2 结果分析

CNM算法能够发现北京大学的大部分院系的社团结构，但人数少且内部联系弱的院系社团结构要弱一些(例如，考古文博学院)。使用3.2中的改进算法，通过删除betweenness最高的若干条边，能够发现这些院系。当预处理中删除25条边时，一个18人的社团被算法找到，其中的17人都来自考古文博学院(参见表5和表6)。

表5 CNM算法的社团发现结果

表6改进的CNM算法的社团发现结果removednum=25(粗体表示新发现的院系)

社团编号社团节点个数节点正确的个数判定的学院151305298医学部88265249信息科学技术学院152147143外国语学院…………1510431历史学系2571817考古文博学院1711515信息管理系…………

不管如何删除边，一些院系仍然无法通过这一方法发现，如表7所示。其中，人数小于50的10个院系中，社会学系、哲学系、心理学系和艺术学院四个没有被发现，这四个院系属于人文社科院系。一般而言，人文社科学生相对活跃，社交圈更为大，容易和不同背景的学生成为好友；而理工科背景的学生相对单一，大多数好友是同院系的同学。

另一方面，人数大于50的17个院系中，仅有国际关系学院的学生(人数为93)难以被聚成一个团体。说明国际关系学院的内聚程度不够高，国关的学生视野广阔，同其他学院的学生有大量的往来，喜好联系。

表7北大本科27个学院的社团识别情况(按学院人数降序排列)

学院编号学院名称学院人数不能被发现的学院27医学部34025信息科学技术学院25921外国语学院14915经济学院13817法学院1231数学科学学院1183物理学院11416光华管理学院1126化学与分子工程学院10825元培学院957生命科学学院9314国际关系学院93√10中国语言文学系888城市与环境学院8424新闻与传播学院674地球与空间科学学院5722马克思主义学院5420政府管理学院442工学院4219社会学系42√11历史学系3418信息管理系3413哲学系24√9心理学系20√12考古文博学院1826软件与微电子学院1823艺术学院11√

6 总结与展望

本文主要研究社交网络的社团结构发掘。一方面，使用了CNM算法发掘社团结构，引入边的betweenness概念，通过删除最高值的边进行预处理来改进CNM算法。另一方面，除了社交网络的结构信息之外，用户的日志内容也被用来辅助改进算法的精度。值得一提的是，本文以人人网上的北京大学学生数据进行实验，挖掘出的社团结构在很大程度上解释了北京大学院系学科的特点。在其他高校是否具有同样的特点，还需要更多的实验来验证。当然，本文的社交对象仅仅关注了在校学生的社区交往情况，没有展示其他层面的社交关系，比如，高校学生毕业后的工作关系。这些问题都将在后续的工作中加以考虑。

未来的工作包括： 如何确定该删除多少条betweenness高的边；引入更多的人人网用户属性(状态、爱好等等)数据进行分析；引入其他的交互数据(比如评论和@等用户交互信息)来进一步精化社团发现的精度；分析除高校外其他层面的社交网络关系。

[1] WattsD J， Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442.

[2] Barabasi A L， Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999, 286(5439): 509-512.

[3] Girvan M， Newman M E J. Community Structure in Social and Biological Networks[J]. PNAS, 2001, 99(12): 7821-7826.

[4] Newman M E J， Girvan M. Finding and Evaluating Community Structure in Networks[J]. Physical Review E, 2004, 69 (2): 026113.

[5] Clauset A, Newman M E J, Moore C. Finding Community Structure in Very Large Networks[J]. Physical Review E, 2004, 70(6): 066111.

[6] Chen J, Community Mining: Discovering Communities in Social Networks[D]. Edmonton, Alberta: University of Alberta, 2010.

[7] Karypis G, Kumar V. Multilevel k-way partitioning scheme for irregular graphs[J]. Journal of Parallel and Distriuted Computing, 1998, 1(48): 96-129.

[8] Satuluri V, Parthasarathy S. Scalable graph clustering using stochastic flows: applications to community discovery[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD). Paris, France: 2009: 737-746.

[9] Kernighan B W, Lin S. An efficient heuristic procedure for partitioning graphs[J]. Bell System Technical Journal, 1970, 1970(49): 291-307.

[10] Ng A, Jordan M, Weiss Y. On spectral clustering: analysis and an algorithm[C]//Proceedings of the 15th Annual Conference on Neural Information Processing Systems (NIPS 2001). Vancouver, British Columbia, Canada: 2001: 849-856.

[11] Nowicki K, Snijders T A B. Estimation and prediction for stochastic blockstructures[J]. Journal of the American Statistical Association, 2001, 96(455): 1077-1087.

[12] Wang X, Mohanty N, McCallum A. Group and Topic Discovery from Relations and Their Attributes[C]//Proceedings of the 19th Annual Conference on Neural Information Processing Systems (NIPS 2006). Whistler, B.C., Canada: 2006: 1449-1456.

[13] Zhang H, et al. An LDA-based Community Structure Discovery Approach for Large-Scale Social Networks[C]//Proceedings of the IEEE Conference on Intelligence and Security Informatics. New Brunswick, New Jersey: 2007: 200-207.

[14] Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E, 2006, 74(3): 036104.

[15] Danon L, et al., Comparing community structure identification[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005(9), 09008.

[16] Scott J, Social Network Analysis: a handbook. 2nd ed[M]. London: SAGE Publications, 2000: 208.

[17] Zhou Y, Cheng H, Yu J X. Clustering large attributed graphs: an efficient incremental approach[C]//Proceedings of the 10th IEEE International Conference on Data Mining (ICDM 2010). Sydney, Australia: 2010: 689-698.

[18] Zhou Y, Cheng H, Yu J X. Clustering large attributed information networks: an efficient incremental computing approach[J]. Data Mining and Knowledge Discovery Journal, 2012, 25(3): 450-477.

[19] Zhou Y, Liu L. Clustering Analysis in Large Graphs with Rich Attributes[J]. Data Mining: Foundations and Intelligent Paradigms, 2012, 23: 7-27.

[20] Hotho A, Staab S, Stumme G. WordNet improves Text Document Clustering[C]//Proceedings of the SIGIR 2003 Semantic Web Workshop. Toronto, Canada: Citeseer, 2003: 541-544.

[21] Hsu W, Lancaster J. Structural link analysis from user profiles and friends networks: A feature construction approach[C]//Proceedings of the 1th International AAAI Conference on Weblogs and Social Media (ICWSM 2007). Boulder, Colorado, USA: 2007: 75-80.