动态几何对学生选择性注意力影响的认知分析

高 媛 江建国

(辽宁师范大学 数学学院，辽宁 大连116000)

0 引言

动态几何软件（Dynamic Geometry Software,简称DGS）是教育价值非常高的软件，在小学、中学、大学等教育领域得到广泛应用。 DGS 主要功能是在计算机上绘制动态几何图形，作图原理与欧式几何理论一致。 目前,世界各国已成功开发了多款DGS，如几何画板（美国）、超级画板（中国）、GeoGebra（澳大利亚）等。

动态几何图形是由DGS 绘制， 其在变化的过程中保持几何关系和性质不变。动态几何图形有两个主要特征：（1）图中的某些对象可以用鼠标拖动或用参数的变化来直接驱动；（2）其它没有被拖动或直接驱动的对象会自动调整其位置，以保持图形原来设定的几何性质[1]。

国内的研究肯定了DGS 对学生学习的积极作用，利用DGS 进行数学实验，不但有利于培养学生的探索能力，而且对思维的深刻性有一定的促进作用[2]。 国外对DGS 在教育中的应用的研究非常宽泛，例如，DGS 对“反证法”论证结构的分析[3]。 Susan K 提出在动态几何环境中，拖动策略和动态几何推理的Van Hiele 层次有直接的联系[4]。

在动态几何学习的过程中， 经常会见到由曲线和线段构成的图片,见图1。当学生看到这样的图片时，首先注意到的是曲线，其次才能分辨直线图形的特点，这个现象称为“直曲现象”，它是学生运用选择性注意力的自然表现。选择性注意则是对外界丰富的信息进行筛选以确保有限的认知资源得以高效运行的认知系统[5]。 注意的选择性维量和信息加工者活动的主动性是选择性注意的先决条件。

图1 直曲现象

学生数学学习效率低与选择性注意习惯有直接关系，目前，国内外对DGS 的研究大多数是从教学实践的角度进行的，而DGS 对选择性注意力影响的探析仍然很少。 本文借助GeoGebra 动态几何软件对选择性注意力在学习过程中的作用进行认知分析，从而达到优化课堂效果，提高学习效率的目的。

1 选择性注意的理论

维特罗克提出的学习生成模型指出：学习过程不是从感觉经验本身开始，而是从感觉经验的选择性注意开始的[6]。在注意的基础上忽略不相关刺激而对相关刺激进行选择就是选择性注意。Terisman 信号衰减理论、特征整合理论以及斯特鲁普效应是目前比较流行的三种选择性注意理论模式[7]。

注意且知觉外来信息的刺激是学生学习活动的开始。选择性注意对学习产生影响至少通过两个控制层面来表现， 其一是通道内选择，针对较低级、单一任务中的情况；其二是任务选择，关于较高级的、双重任务与执行功能有关的选择。主动的、有目的、有选择的信息加工过程是学习过程。 它是依据现有的学习内容、兴趣、先前的知识、经验来实现的。因此，学习者学习的必要条件是对相关信息保持觉醒，同时进行选择性注意。

选择性注意学习策略是指学习者在学习情境中激活与维持学习心理状态，将注意集中在有关学习信息或重要信息上[8]。 该策略的使用，要求学习者从三个方面进行信息的选择：一是选择性编码,目的是从大量无关信息中筛选出相关信息；二是选择性组合,有选择地将已编码的信息以某种合理的方式组合起来，形成一个有机的整体；三是选择性比较,将新获得的信息与过去经验相比较，建立起联系。

通过这种学习策略，学习者严格筛选进入大脑的信息，保证大脑编码、贮存、加工信息，同时有效地抑制了干扰刺激，保证对相关信息的高效加工，见图2。 因此，选择性注意学习策略对提升学习效果具有重要的促进作用[9]。

图2 信息加工过程

2 动态几何图形的认知特性

2.1 视觉敏感性

刺激的特征，如：性质、数量、空间分布、与主体的关系等是影响选择性注意的主要因素。就刺激物理特征而言，有差异的刺激，如：形状、大小、强度、颜色、位置等能够唤醒学生选择性注意力。 根据Terisman信号衰减理论，学生事先注意并分析了刺激的物理特性，对于具有目标特性的刺激，把信号传到下一个阶段，而对于没有目标特性的刺激，我们把它仅仅当作弱化刺激。

颜色是引起视觉的重要属性，颜色的不同将引起学生的选择性注意力。由Geogebra 可以作出具有色彩特征的图片，见图3，“红色”刺激将会吸引学生注意，同时弱化其他颜色的刺激。 所以，教师应该将“颜色标注法”贯穿于教学活动吸引学生选择性注意力，增强视觉敏感程度，提升课堂效果。

图3 颜色标注

2.2 视觉范围性

研究显示，落在中央凹（视网膜中心2 球面度范围内的区域）和中央视野（视野中心水平8 度，垂直6 度范围的椭圆区域）的物体可以获得最清晰的视像[10]。因此，使用Geogebra 中“滑杆”功能描绘图形对称、全等、旋转图形时，见图4，要考虑人眼的注视幅度和左右的不同分配，从而限定“滑杆”的范围。两个对称图形的距离不宜过大、旋转的速度不宜过快，否则会影响学生注意力的选择，加大了注意和认知负荷，给学习带来干扰。

图4 三角形的旋转

2.3 直观感知性

学生对几何的认知水平是不同的，皮亚杰认为空间知觉能力经历拓扑性、投影性和欧几里得性[11]。 几何学习涉及三种认知过程：(1)视觉过程：几何结论的复述、探析复杂几何问题，主观证明的空间表示；(2)推理过程: 知识拓宽、证明和解释的过程；(3)构造过程：图形的构造是呈现的数学对象的表达和观察结果的模型。 杜福尔的研究[12]认为：三种认知过程必须独立地发展；不同的人的视觉过程和推理过程是不同的，应该予以恰当的区分；而只有经过恰当的区分，这三种过程才能协调地发展，见图5。

图5 认知过程

由于演示实验能够得到灵感，变化的刺激物比静止的刺激物更能引起注意，Geogebra 动态几何软件可实际地变动图形， 增强学生的选择性注意力。变更图形的方式大致可分为下列几种：分解组合图形、放大缩小图形、平移旋转图形等、以不同的方式更改图形之后，能够得到操作性的理解。 这些操作可使图形具有启发性的功能，故可以在操作过程中突显出图形的变化，从而得到某个证明步骤或解题的灵感。

例如，运用Geogebra 展示圆与直线的位置关系，使原本静止的直线运动起来， 学生能够亲自动手实验， 总结出圆与直线具有相切、相交、相离的关系，见图6。 演示实验是施展教学艺术的独特方法。 借助它足以刺激学生的选择性注意，唤起学生的新奇感，激起学生的求知欲，最终提高学生的听课效率。

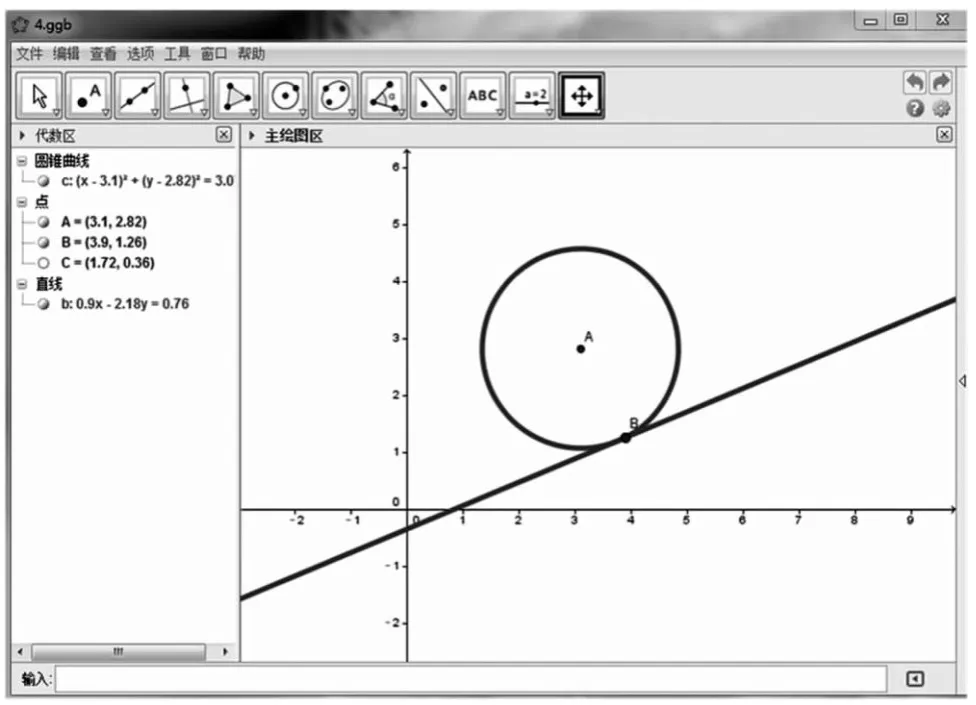
图6 圆与直线位置关系

2.4 目标明确性

学习活动的出发点和落脚点是学习目标，其是学生对学习结果的期望。学习目标在学习中发挥重要作用，学生有选择地加工信息，确定目标并加以注意是学生运用选择性注意力的主要体现。 在课堂教学中，设定学习目标是引导学习者期望的重要手段，它对学习起着定向和标准作用。

学习者的期望(心向)能对注意指向产生强烈的影响，是否有明确的目标影响着学习方向的确定和学习标准的选择，目标不同，注意倾向也不同，学生的学习策略和心理努力也不一样。因此，学习活动的主要任务是树立目标意识并且学会确定学习目标。发挥学习目标的指导作用，有选择地注意与目标有关的信息，使学生带着学习目标进行心理活动，发挥选择性注意力的作用。

学习目标的确定与问题的提出方式有重要关系，提出问题的方法是保持高度警觉、吸引学生选择性注意的策略。 因此，在数学教学中，教师可针对新知识通过创设问题情境或直接提出与新知识有关的问题来达到。 动态几何教学中，教师提出问题，三条高线是否交于一点？学生运用Geogebra 动态几何软件作出三角形的三条高线， 便可以发现问题的结论，并且利用Geogebra 动态几何软件中“拖拽”功能改变三角形的形状（直角三角形，钝角三角形、锐角三角形），学生主动探索结论，见图7。 确定目标的方法利于忽略不重要的信息，加强注意重要的信息，使学生有意识地进行选择性注意。Geogebra 创设的情境，有利于调动学生多种知觉系统的功能，增强学生的学习兴趣，促进学生积极的反思，引发学生对这个结论的进一步思考，进一步探究。

2.5 知识创新性

注意过程中包含朝向反应。 朝向反应有两个特征：知识材料的新颖性和习惯化。教师必须认识到，只有知识材料新颖有趣，才能充分唤醒学生，引发学生的学习兴趣，吸引他们有选择地进行注意。而知识的重复呈现会形成习惯化，只会削弱知识的新颖性，难以诱发朝向反应。在新时期的教学过程，尤其是动态几何问题的教学，需要运用新颖有趣的教学材料。 在抛物线的讲解中，运用一张“愤怒的小鸟”游戏图片作为背景，见图8，还可以利用这样的游戏问题引入教学重点问题，轻松而快乐的学习活动使教学朝着正向发展，完成教学任务。

3 结束语

DGS 有助于在解决几何问题的过程中，帮助学生通过猜想与实验去发现解题思路，也有助于教师制作典型例题，变换表征形式，检验学生的解释等。 在适当的数学教学问题中，将DGS 和选择性注意策略的认知方法相结合，合理地使用DGS 可以增强学生的选择性注意力，提高学生的记忆力，让学生从对几何的感性认识上升到理性认识，培养学生对几何的兴趣。学生寻找新的学习技巧，突破传统教学，能够在教学活动中巧妙使用选择性注意力，从而快速理解教学活动，达到深入挖掘知识精髓的程度，达到提高教学水平的目的。

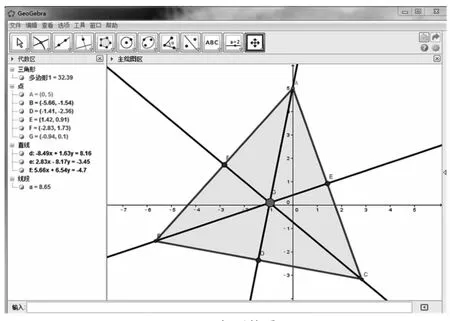
图7 三角形的重心

图8 愤怒的小鸟

有研究者提出，DGS 在数学教学中是否有意义， 取决于学习者自身的知识基础，如果学生不具备一定的几何知识的前提下，大量地使用DGS 会不会损害学生的几何思维？ 教学是否应从学生已有的认知结构出发，用概念的形成方式教学效果会如何？ 这些都是今后研究的重点。

［1］张景中，江春莲，彭翕成.《动态几何》课程的开设在数学教与学中的价值[J].数学教育学报，2007，16（3）：1-5.

［2］陶维林.在 CAI 中用《几何画板》进行素质教育[J].数学通报，2001，40(2)：14-16.

［3］Baccaglini -Frank,A.Antonini,S.Leung, A., Mariotti,M.A.Reasoning by contradiction in dynamic geometry[J].2013，7(2)：63-73.

［4］Susan K.Forsythe.Linking dragging strategies to levels of geometrical reasoning in a dynamic geometry environment[J]//Smith, C.(Ed.) Proceedings of the British Society for Research into Learning Mathematics 33(2),2013.

［5］Downing P E.Interactions between visual working memory and selective attention[J].Psycholgical Science,2000，11（6）：467-473.

［6］张建伟，陈琦.从认知主义到建构主义[J].北京师范大学学报，1996，41(4)：75-108.

［7］Robert J.Sternberg.认知心理学[M].北京：中国轻工业出版社，2006.

［8］肖谷清,肖小明,谢祥林.选择性注意策略在化学教学中的运用[J].化学教育，2005.

［9］周详，沈德立.高效率学习的选择性注意研究[J].心理科学，2006，29(5)：1159-1163.

［10］黄艳群，黎旭，力荣丽.人机界面[M].北京：北京理工大学出版社，2007.

［11］鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

［12］Duval,R.Geometry from a cognitive point of view[M]//C.Mammana&V.Villani(Eds), Perspectives on the Teaching of Geometry for the 21st Century,An ICMI Study[Chapter2.2].The Netherlands:Kluwer Academic Publishers,1998.