装备备件供应保障研究

罗 卫 宋翰林

（中国人民解放军91663 部队，山东 青岛 266071）

0 前言

备件供应保障是确定装备使用与维修所需备件的品种和数量，并解决它们的筹措、分配、供应、储运、调拨以及装备停产后的备件供应等问题的管理与技术活动。其目标是使装备使用与维修中所需备件能得到及时和充分的供应，并使备件的库存费用降至最低。为此，备件供应保障主要解决两个方面的问题：一是，确定装备备件的需求量，主要是确定保障时效期内备件的品种和需求量，备件的需求量与装备上工作部件的可靠性和使用时间有密切的关系；二是，确定装备备件的库存量，库存量的大小取决于对库存量的合理控制[1]。上述两个方面的问题由于受诸多不确定因素的影响，因此要准确、合理地确定备件的需求量和库存量实际上是极其复杂的工作。

1 备件的分类

（1）按供应的时间可分为：

安装备件：保障设备/系统安装所需的备件，包括在安装、试验和评价维修设备/系统所需的常用和散装件（如连接件、电缆）以及零部件。

初始备件：在装备部署初期（1～2 年），用于保持和恢复装备设计性能所必需的不可修复件和部分可修复件。不可修复件包括消耗性备件和部分易损坏备件。 可修复件主要提供修理周转的更换件。 初始备件是从承制方那里采购 （或者是承制方制造或者是承制方从转承制方、供应方得到）的。

后续备件：在装备稳定使用阶段，为保持和恢复装备的设计性能所必需的可修复件和不可修复件。 该类备件是承制方向使用方推荐的订货备件，作为已消耗掉的初始备件的补充件，由使用方选择订货。

（2）按寿命分布分为：

指数寿命件：其故障率为常数；

正态寿命件：其故障率依赖时间；

威布尔寿命件。

（3）按结构属性分为：

电子件备件：其寿命分布一般按指数分布处理；

机械件备件：其寿命分布一般可按正态分布处理，属限寿件，按寿命长短又可进一步划分为全寿件 （整个服役期内除执行规定的保养外，不需翻修）、单寿件（对应一个浴盆盆底长度即翻修时限）、短寿件（基层级预防维修件，也叫易损件备件）；

其它件备件：如橡塑件、木材等，一般不假定寿命分布，其寿命按经验数据给出，也归入限寿件。

（4）按可恢复性分为：

可修复件备件：可以通过修复性维修恢复其全部规定功能的件的备件；

不修复件备件：不能通过修复性维修恢复其全部规定功能或不值得修复的件的备件，又称为一次性备件。

（5）按备件存放时的状态分为：

待修备件：不能使用的可修复备件；

准备发放备件： 具有使用功能和满足操作规范的可以发放的备件，该备件可以是新的、修复的或大修好的。

（6）按维修级别分为基层级备件、中继级备件和基地级备件。

（7）从购置费用角度分为昂贵件和一般件。

（8）从对系统功能影响角度分为关键件和一般件。

（9）从标准化角度分为标准件和非标准件。

（10）按供货源分为通用件（市售件）、专用件（制造厂产品）。

2 备件消耗因素分析

备件消耗率反映了装备的可更换单元对备件需要的程度。引起备件消耗的因素是多方面的，它不仅与可更换单元的故障率有关，而且与维修策略、使用管理、零部件对损坏的敏感性等多种因素相关。在预计备件消耗率时，应考虑下述因素的影响[2]。

（1）可更换单元的基本故障率（λ）

基本故障率是指当可更换单元的环境因素、质量等级、工作状态等都符合规定的基准条件时，该可更换单元的故障率，它仅与可更换单元的种类、结构、工艺有关。可更换单元的故障率对备件消耗率有着最直接的影响。故障率从可更换单元本身的固有可靠性反映出使用过程中需要备件的趋势。提高可更换单元的固有可靠性是降低备件消耗率的根本措施。 但可更换单元的故障率并不等于备件消耗率。 装备发生故障后不一定都需要备件，而装备未出现故障时，由于人为损坏或丢失备件，或进行预防性维修等却有可能需要备件[3]。

（2）环境影响因素

装备所处的环境不同，其可更换单元的备件消耗率可能会大不相同。 参考可靠性预计方法和外军的研究， 将装备的使用环境分为好、中、差三类。不同结构属性的部件受环境的影响程度也不同：对于电子器件，由于温度、湿度、风沙、振动等环境因素影响，其备件消耗率会较大，所以其环境影响系数较大；非电子产品中的非金属件次之；而金属件受环境因素影响最小。各类器件对应不同环境的环境影响因子见表1。

表1 环境影响系数

（3）零部件对损坏的敏感性

在装备搬运、装配与维修中，可能因人为差错、不按操作规程和严酷使用等而使备件遭受损坏。在装配时，可能因安装工具而损坏备件，在维修时，也可能由于调整不当等损坏备件，这是由于人为差错造成的，与该件本身的故障率并无关系，它与零部件对损坏的敏感性有关。敏感性系数取值见表2。

表2 敏感性系数

（4）修复性影响因素

故障单元修复后，仍可作为备件继续使用，修复性影响考虑的就是单元故障后， 可修复比例对备件消耗的影响。 决策时， 可以根据FMEA 和相似产品的数据直接给出修复比例。 另外，也可以对修复性进行分类，分为可修、部分可修和不可修三类，对应的修复性影响系数见表3。

表3 修复性影响系数

（5）使用频率

预计备件消耗率时，必须考虑可更换单元的使用频率。 正常使用与非正常使用对备件消耗率也有着较大的影响。 非正常使用一方面表现为使用时间过长或应力应变状况超出原设计规定的使用条件；另一方面，则表现为由于使用过少或没有使用（如未定期通电、开机、运转等），造成某些零部件变质或性能下降。 使用频率系数取值见表4。

表4 使用频率系数

（6）备件管理

零部件因松动而脱落，在维护、修理和保管中丢失以及因保管不善而造成的备件失效等，都会引起备件消耗量的增加。

（7）预防性维修消耗

在预防性维修中，特别是定时更换策略下，所导致的备件消耗。备件的预防性维修消耗数等于年度预防性更换次数，该值依装备的预防性维修方案、计划而确定。

3 备件的供应模型

备件数量是备件供应保障过程的核心问题。确定某项备件数量所涉及的重要因素有很多，包括：该备件的可靠性；装备上使用该备件的数量；备件可用概率；该备件对任务成败的关键性；该备件的费用等。就装备维修来讲，在确定备件要求时应当考虑到：

（1）修复性维修和预防性维修实际所需备件。

（2）补偿因在实施维修过程中可修复件的维修周转所需备件的额外储备。 用备件换下可修复件送修至修复返回作为备件，需要维修周转时间，特别是中继级或基地级维修工作繁忙，需等待时间愈长，补偿所需的备件数就愈多。

（3）补偿因采购备件从订货到交货的时间所需备件的额外储备。

（4）补偿可修复件无法修复而报废所需备件的额外储备。

3.1 初始备件的供应模型

备件数量主要取决于装备中该部件的数量及它的寿命分布规律。据统计，寿命服从指数分布的部件约占全部部件的90%左右，电子件的寿命分布一般均可按指数分布处理。下面我们寻求指数寿命件备件需求量的计算模型[4]。

设装备中第种部件的寿命服从指数分布，故障率为λ，装备在两两不重迭的各个时间间隔]中，该类部件出现的故障相互独立，且在[t,t+Δ t ]内最多出现一个故障(Δt→0)，即：

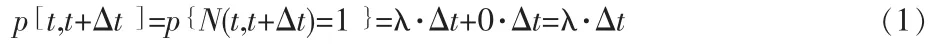
Δt→0 时，0·Δt 为高阶无穷小，那么在 [0,t ]内，当备件量kpi为零，即kpi=0 时，装备的可靠工作概率为：

当备件量kpi=1 时，装备的可靠工作概率为：

当备件量kpi=k 时，装备的可靠工作概率为：

这样根据系统可靠工作的概率要求和第种部件的平均故障率，就可以计算出该种备件的需求数量。 于是我们可以得到：

若装备中某部件的寿命服从指数分布，该部件的备件需求量可按下式确定：

其中：P——装备中某部件要求的备件保障度；

j——递增变量，从0 开始逐一递增至某s 值，使上式右边值≥P；

s——所需备件数量；

n——装备中该部件的件数；

λ——该部件的故障率；

t——保障时效内装备累积工作时数， 对不同情况t 应分别处理：

（1）对不可修复件，t 取保障时效期内装备累积工作时数（h）或备件更新周期内装备累积工作时数（h）；

（2）对可修复件又分两种情况：①基层级更换，后送中继级或基地级修复，此时取修理周转期内装备累积工作时数（h）；②在基层级对该件进行修复，此时当满足该件的平均故障间隔时间（MTBF）远大于该件的平均修复时间（MTTR）时，在至少准备一个供换件修理的情况下，t 取该件的 MTTR（h）。

3.2 后续备件供应模型

随装备一起交付部队的初始备件，是研制单位根据装备的各种战技术性能和相似装备的备件消耗情况而配备的，只能体现装备备件消耗的一般规律。 后续备件是装备进入稳定使用阶段需求的备件，体现的是该装备备件消耗的具体规律，由使用部队根据装备初始保障期的实际使用情况，统计备件消耗规律，修订初始备件供应而确定的。一般由使用部队向军械处申报下一年需请领的备件计划，所以后续备件供应一般以年为单位来计算，也可称为年度备件需求量。

如果装备使用信息收集的及时完整，并且能够准确地确定零部件的预防性和修复性维修更换间隔时间，则可按下述模型计算：

（1）对不可修复件，确定备件数量的计算模型为：

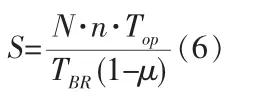
式中：S——所需备件数；

N——装备总数；

n——每台装备上该部件的件数；

Top——供应保障计划时效期；

TBR——部件的平均维修更换间隔时间

TBRpt——预防性维修更换间隔时间；

TBRct——修复性维修更换间隔时间；

μ——备件废品率。

（2）对可修复件，其修复后将归入周转备件继续使用，所以确定的是周转期内的备件数量，计算模型为：

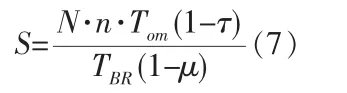
式中：Tom——备件修复周转时间；

τ——修复后可继续使用的百分数。

4 结束语

本文通过对各种影响备件消耗因素的分析，针对耗损类型的备件和可修复类型的备件，建立了数学模型。 通过该模型可以预计装备工作在标准条件下的备件需求量，以准确地反映装备备件供应保障的实际情况，为装备综合保障决策提供科学的依据。

［1］陈学楚.装备系统工程[M].北京：国防工业出版社，2005.

［2］李建平，石全，甘茂治.装备战场抢修理论与应用[M].北京：兵器工业出版社，2000.

［3］周正伐.可靠性工程基础[M].北京：宇航出版社，1999.

［4］方龙耀.弹药仓库保障力量需求数学计算模型探讨[J].仓储管理与技术，2005.