线性回归的分布式压缩采样算法

张 波，刘郁林，常博文，张建新

(重庆通信学院DSP研究室，重庆 400035)

0 引言

无线传感器网络(wireless sensor networks，WSNs)［1］凭借其部署灵活、抗毁性强、高容错等独特优势，被广泛应用于数据采集与监测应用［2］。在这些应用中，传感器节点通常按照固定的时间间隔对周围环境信息进行采样，并将采样获得的大量数据经多跳路由方式传输到sink节点。传感器节点的能量有限，大量的数据传输任务会造成节点能量的过快消耗。因此，在保证数据精度满足用户需求的前提下，采用能量有效的数据收集策略，尽量减少整个网络的数据传输量是节约节点能耗、延长网络生命周期的有效方式。

WSNs具有时空相关性。利用节点间的空间相关性，某个特定节点的数据可以从周围节点的数据预测得到;利用节点的时间相关性，节点当前时刻的数据值可以从该节点的历史数据预测得到。可预测的数据不发送到sink节点是节约节点能量的一种有效方式［3］，基于这种思想，近年来国内外研究者将预测理论应用到WSNs中以减少数据收集的通信开销［3－11］。宋欣等［4］应用线性回归分析方法构建感知数据模型，保持感知数据的特征，使节点仅传输回归模型的参数信息，代替传输实际监测的感知数据信息，显著地减少了数据传输量，但是该方法需要在能量有限的传感器节点处计算模型参数，需要大量的计算开销。Chatterjea等［5］将时间序列预测理论应用到WSNs，提出了一种基于时间序列预测的自适应采样算法，该方法可根据预测误差来调节节点的采样速率，但是低速率采样可能导致错失重要事件。为尽可能避免错失重要事件，在其后续的研究中，提出了一种利用节点间相关性增加时间覆盖的随机调度方法［6］，但该方法无法从根本上避免错失重要事件。文献［7－10］提出了一种双预测算法，该方法仅将预测误差大于误差容限的采样值传输到sink节点，显著减少了整个网络的数据传输量。但是该方法存在以下缺点:①模型参数的反向传输需要带来额外的通信开销，降低了该算法的有效性;②预测算法需要消耗节点有限的计算资源;③节点采样得到的大量数据被直接丢弃，浪费了宝贵的采样资源。

本文将线性回归和压缩感知(compressed sensing，CS)［11－12］理论相结合，提出了一种基于线性回归的分布式压缩采样算法。该方法只需少量节点(称为参考节点)以等间隔采样模式工作，其他节点以低速率的压缩采样模式工作。sink节点接收到各个节点的数据后，首先，利用参考节点的信号序列预测出其他节点的信号序列，然后，利用其他节点对应的压缩采样序列纠正预测误差，实现节点数据的高精确重构。

1 基于线性回归的分布式压缩采样算法

1.1 分布式压缩采样原理

部署在监控区域的传感器节点可依据节点数据的相关性划分成若干簇，设位于同一簇中任意两节点的数据均显著线性相关，(为保证阐述的流畅性，将在2.1节中详细探讨确保同一簇中任意两节点的数据均显著线性相关的分簇算法。)考虑到提出的采样方法中，各簇工作原理相同，为叙述简单而不失一般性，现以一个簇的工作方式为例进行阐述。

设WSNs一个簇中有J个节点，各节点同步采样，经过一段时间采样后各节点均采样得到一个长度为 N 的信号向量，记为 xi∈RN，i=1，2，…，J，节点相应的一阶差分信号序列Δxi∈RN－1可按如下方式定义

(1)式中:xi(t)(t=1，2，…，N)是节点 i第 t时刻的信号值;Δxi(t)(t=1，2，…，N －1)是节点 i第 t时刻的一阶差分信号值。

设节点 i和 j(j=1，2，…，J，且 j≠i)是位于同一簇中的两相异节点，由于同一簇中任意两节点的数据均显著线性相关，因此，节点j的一阶差分信号序列可用节点i的一阶差分信号序列表示为

(2)式中:β0和 β1为回归系数;u∈RN－1的各元素服从均值为零、方差为σ2的高斯分布。

(6)式右边的前两项称为抽样误差，最后一项称为总体误差的方差。如果预测精度满足一定要求，那么预测误差的大多数项均接近于0，即预测误差e是可压缩信号，设其稀疏度为K。考虑到预测误差向量的稀疏性，因此，可利用CS理论纠正预测误差，从而实现节点数据的高精度重构。下面以节点i和节点j信号的采样和重建为例，阐述分布式压缩采样算法的实现过程。

节点i依然按等间隔方式采样，将采样后的信号向量xi经多跳路由传输至sink节点。

(7)式中，yj∈RM为测量值构成的向量。节点j的编码过程如图1所示。

由于e的稀疏度为K，根据CS理论可知，当节点j的测量值个数满足M≥cK log(N/K)时(c为常数)，采用基追踪(basis pursuit，BP)［13］或正交匹配追踪(orthogonalmatching pursuit，OMP)［14］算法可精确重建出误差向量。

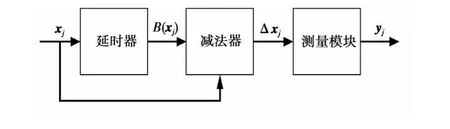
图1 编码框图Fig.1 Block diagram of encoding

设节点j的初始采样值为xj(1)，那么通过(11)式可计算出节点j各个采样时刻的信号值，从而实现节点j信号的精确估计。

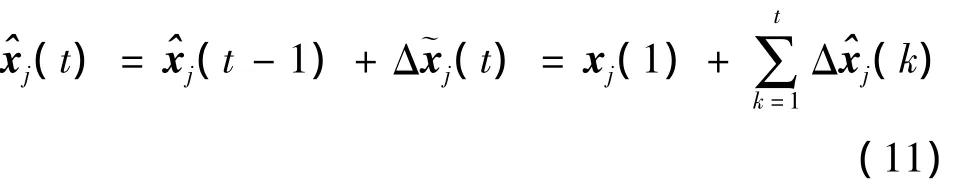
由以上分析可知，综合运用线性回归和CS理论，可按照图2所示方式精确估计出节点j的信号序列。

图2 解码框图Fig.2 Block diagram of decoding

首先，利用线性回归理论，从节点i的差分信号序列预测(近似估计)出节点j的差分信号序列;然后，利用节点j的测量值校正预测误差，从而得到节点j差分信号序列的精确估计;最后，通过累加运算由节点j的差分信号序列计算得到节点j的信号序列。

1.2 分布式压缩采样实现步骤

根据上述的分布式压缩采样原理，可将提出的采样方法分为3个工作阶段:成簇阶段、原始数据采样阶段和分布式压缩采样阶段。

成簇阶段。各节点按固定周期同步采样，将节点的原始数据传输到sink节点。sink节点根据各节点采样数据的相关性对传感器网络进行分簇。

原始数据采样阶段。各节点按固定周期同步采样，将节点的原始信息传输到sink节点。sink节点在每个簇中随机选择一个节点作为参考节点，然后根据各节点的信号序列计算出各非参考节点相对于参考节点的回归系数和真实信号与预测信号差值信号的稀疏度。该阶段又可称为训练阶段。

分布式压缩采样阶段。在该阶段，参考节点按固定周期采样，其他节点按照(7)式进行压缩采样。sink节点收到各节点的数据后，首先，根据参考节点的数据近似估计其他节点的数据，然后，利用其他节点的测量值向量纠正预测误差，从而实现节点数据的高精度重构。

按照数据的处理流程，具体实现过程如下。

1 )各节点按固定周期同步采样，并将采样数据以时分复用方式传输到sink节点。sink节点接收到各节点的数据后，对各节点的数据进行相关性分析，将显著线性相关的传感器节点划分到同一个簇中。

2 )依据节点的剩余能量，在每个簇中选择一个能量充裕的节点作为参考节点，根据历史数据计算其他节点相对参考节点的回归系数。

3 )根据阈值ε和预测误差估算预测误差向量的稀疏率。

4 )参考节点按固定周期采样，收集节点的原始数据;其他节点根据估算得到的稀疏率和设定的采样窗口长度，确定压缩采样速率下限，将节点原始数据投影到低维空间。

5 )sink节点收集到各节点数据后，首先，采用参考节点的信号序列预测各非参考节点的信号序列，然后，采用CS理论纠正预测误差，从而精确估计各非参考节点的信号序列。

2 分布式压缩采样算法实现细节

2.1 相关性分簇算法

由前面分析可知，确保划分到同一簇中的任意两节点采样数据均显著线性相关是提出算法能够成功实现的基础。然而现有的成簇算法一般根据节点地理位置的邻近关系分簇，这有益于节约簇内节点相互通信的开销，但却无法保证位于簇内的任意两节点之间均具有良好的相关性。为此，本节将给出一种相关性分簇算法，该算法依据节点数据相关性对WSNs进行分簇，可确保划分到同一簇中的任意两节点采样数据均显著线性相关。

设位于监控区域的传感器节点对感知区域的信息同步采样，并将采样得到的数据经多跳路由方式传输到sink节点。sink节点将各节点的数据存储下来，设N为经过一段时间的数据采集后各个节点采集得到的信号向量的长度，L为位于监控区域的传感器节点个数，那么sink节点接收到的数据可用一个N×L的矩阵表示为

矩阵X的每一列 xi，i=1，2，…，L表示单个传感器节点采样得到的信号向量，矩阵X的每一行xj，j=1，2，…，N 表示所有传感器节点同一时刻采样值构成的信号向量。

sink节点接收到数据之后，可计算出任意2个节点之间的相关系数

(13)式中:xi(k)，xj(k)分别是节点i和j第k时刻的采样值;¯xi，¯xj分别是节点i和j采样值的算术平均值。

依次计算得到任意两节点间的相关系数后，可将相关系数写成相关系数矩阵形式为

显然，矩阵R是关于主对角线的对称矩阵。

要检验节点i和j之间线性相关程度是否显著，

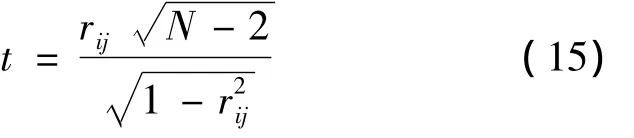
对于给定的α(α为置信概率)和自由度(N－2)，查t分布表可得到 tα/2(N －2)的值，如果|t|＞tα/2(N－2)，那么就称xi与xj的线性关系显著。

为衡量某个特定节点i与多个节点集合Ω={j1，j2，…，jk}的相关性，定义平均相关度为可用样本的相关系数rij构造一个检验统计量为

为确保划分到同一簇中的任意两节点采样数据均显著线性相关，考虑如下分簇算法，该算法的思想是:先将2个最不相关的传感器节点分别划分到2个簇中，然后，其他节点以平均相关度为依据依次划分到这2个簇中。算法的输入为相关系数矩阵，输出为各簇节点的索引集合，具体步骤如下。

1 )初始化簇内节点编号集合:

该算法可将监控区域的节点划分为2个簇，空间相关性强的传感器节点被划分到同一簇中。按照上述算法可进一步将一个大的簇划分为更小的簇，直到每个簇内节点之间的相关性均满足应用需求。

2.2 误差向量稀疏率估计

而Var(u(k))=σ2，σ可由历史数据的u估计得到

因此，当N取值足够大时，预测误差的方差可由(21)式确定。

一般情况下，可根据应用要求设定阈值ε，若预测误差的绝对值小于ε，则视为精确重构。设预测误差位于区间［－ε，ε］的概率为1－S，则有

即，预测误差超过设定阈值的概率为S，该值即为预测误差信号向量的稀疏率。

3 实验仿真

本节将通过仿真实验来验证提出算法的有效性。实验数据采用Intel Berkeley实验室提供的实测数据［15］。该传感器网络由54个Mica2传感器节点组成，节点的位置分布如图3所示。在该传感器网络中，每个传感器节点周期地探测温度、湿度、光照等信息，采样周期为31 s。不失一般性，选择节点1作为参考节点，节点2作为非参考节点，各非参考节点的工作方式相同，现以节点1和节点2的采样数据进行仿真实验。实验仿真包括2个部分:①验证节点1和节点2的一阶差分信号序列之间的线性相关性;②以节点2采样数据的预测和校正为例验证提出分布式压缩采样算法的有效性。

图3 Intel Berkeley实验室传感器节点分布Fig.3 Layout of the WSN of the Intel Berkeley research lab

3.1 节点数据的相关性

首先通过仿真验证节点1和节点2采样数据的相关性。

图4是节点1和节点2第1天(2004年3月1日)温度序列的对比图，由图4可以看出，两节点的温度信号序列具有相同的变化趋势，具有很强的相关性。

图5是节点1和节点2第1天一阶差分信号序列的散点图，由图5可看出，节点1和节点2的一阶差分信号呈线性相关关系，利用线性回归理论可求得相应的回归系数，图中直线是回归直线。

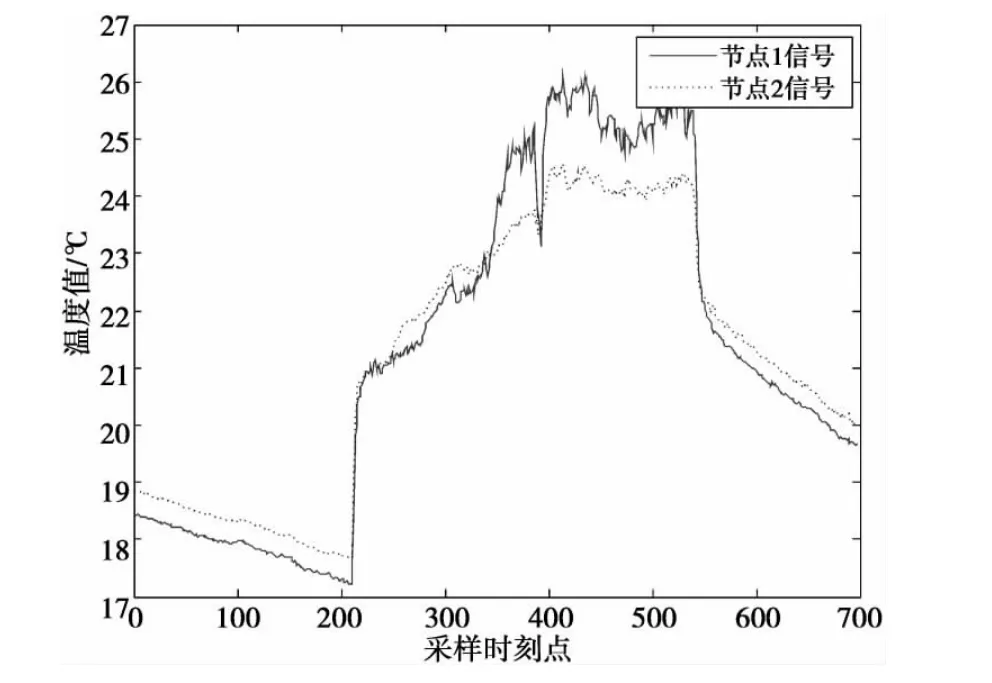
图4 两节点原始信号对比Fig.4 Comparison between the original signals of two nodes

图5 两节点差分信号序列的散点图Fig.5 Differential signal sequence scatter diagram of two nodes

图4和图5的仿真结果表明:节点1和节点2的一阶差分信号序列是显著线性相关的。

3.2 分布式压缩采样算法的有效性

下面通过实验仿真验证提出的分布式压缩采样算法的有效性。设定误差容限ε=0.1℃，利用节点第一天的数据可估计得到预测误差向量的稀疏度K=75。根据CS理论可知，要确保预测误差向量精确重构，测量值个数应满足M≥170。

节点2第2天(2004年3月2日)的温度信号序列可由节点1第2天的温度信号序列预测得到，相应的预测误差为0.031℃。图6是节点2第2天原始信号和预测信号在采样时刻［500，550］的对比图。由图6可以看出，除少数时刻存在较大的偏差外，预测信号的曲线几乎和实测信号曲线重合。

利用节点2第2天的测量值向量可纠正预测误差，纠正后的相对误差为0.001 5℃。图7是在节点2的测量值个数M=200的情况下，节点2第2天实测信号和经CS纠正后预测信号在采样时刻［500，550］的对比图。由图7可以看出，预测过程产生的预测偏差得到了纠正，纠正后的信号几乎和原始信号完全重合。

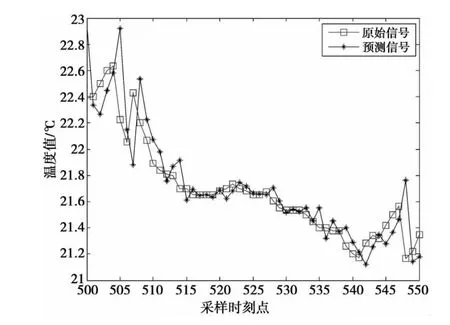
图6 原始信号与预测信号对比Fig.6 Comparison between the actual sequence and the estimated sequence

图7 原始信号与纠正后预测信号Fig.7 Comparison between the actual sequence and the corrected sequence

根据图6和图7的仿真结果，可从重构精度和采样值个数2个方面分析提出算法的有效性。

1 )重构精度。节点2温度信号的预测误差为0.031℃，而经过CS纠正后相对误差仅为0.001 5℃，即，经过误差纠正后，数据的估计精度提高了一个数量级。

2 )采样值个数。采用提出的算法节点2每天仅需采样和传输200个数据值即可在sink节点高精度重构出节点2的原始数据，而采用传递原始数据的办法需要采样和传输697个信号值。因此，与传递原始数据相比，提出的方法可减少节点71%的采样值个数。

上述仿真结果表明，提出的算法可以在保证数据精确重构的前提下，大大减少节点的采样值个数，进而减少整个网络的数据传输量。考虑到节点能耗和网络数据传输量成正比，因此，提出的算法可显著降低数据收集的通信能耗。

4 结语

本文将经典的线性回归和压缩感知相结合，提出了一种基于线性回归的分布式压缩采样算法，该算法先采用线性回归近似估计节点的信号序列，然后采用压缩感知纠正预测误差，实现了低速率采样条件下节点数据的高精确重构。由于预测的精度依赖于节点间的相关性，为保证提出采样算法的有效性，还提出了一种相关性分簇算法，该算法可以将感知数据显著线性相关的传感器节点划分到同一个簇中。仿真结果表明，与等间隔采样相比，在重构误差为10－3数量级时，该算法减少了71%的采样值个数。

［1］AKYIDIZ L F，SU W，SANKARASUBRAMANIAM Y，et al.A survey on sensor networks［J］.IEEE Communications Magazine，2002，40(8):102－114.

［2］孙书诚，郎朗，苏长杰.带有时间/地理标签无线传感器网络的农业环境远程实时监测系统［J］.重庆理工大学学报:自然科学，2013，27(3):104－108.

SUN Shucheng，LANG Lang，SUChangji.The agricultural environment remote real－timemonitor system of The wireless sensor network with label of time and geography［J］.Journal of Chongqing University of Technology:Natural Science，2013，27(3):104－108.

［3］LIU C，WU K，PEIJ.An energy－efficient data collection framework for wireless sensor networks by exploiting spatiotemporal correlation［J］.IEEE Trans on Parallel and Distributed Systems，2007，18(7):1011－1023.

［4］宋欣，王翠荣.基于线性回归的无线传感器网络分布式数据采集优化策略［J］.计算机学报，2012，35(3):568－580.

SONG Xin，WANG Cuirong.Linear regression based dis－tributed data gathering optimization strategy for wireless sensor networks［J］.Chinese Journal of Computers，2012，35(3):568－580.

［5］CHATTERJEA S，HAVINGA P.An adaptive and autonomous sensor sampling frequency control scheme for energy－efficient data acquisition in wireless sensor networks［C］//4th IEEE International Conference on Distributed Computing in Sensor Systems(DCOSS).Santorini，Greece:Conference Publications，2008:60－78.

［6］CHATTERJEA S，HAVINGA P.Improving temporal coverage of an energy－efficient data extraction algorithm for environmentalmonitoring using wireless sensor networks［J］.Sensors，2009，9(6):4941－4954.

［7］LIU C，WU K，MIN T.Energy efficient information collection with the ARIMA model in wireless sensors networks［C］//Proceedings of IEEE Global Telecommunications Conference.st.Louis，USA:Conference Publications，2005:2470－2474.

［8］MATOS T B，BRAYNER，MAIA A，et al.Toward innetwork data prediction in wireless sensor networks［C］//Proceedings of ACM Symposium on Applied Computing.New York，NY，USA:ACM，2010:592－596.

［9］CARVALHO C，GOMES D G，AGOULMINE N，et al.Improving prediction accuracy forWSN data reduction by applying multivariate spatio－temporal correlation ［J］.Sensors，2011，11(11):10010－10037.

［10］CARVALHO C，GOMES D G，AGOULMINE N，et al.Multiple linear regression to improve prediction accuracy in WSN dazta reduction［C］//Proceedings of 7th Latin A－merican Network Operations and Management Symposium.Quito，Ecuadov:Conterence Publications，2011:1－6.

［11］BARANIUK R G.Compressive sensing［J］.IEEE Trans on Signal Processing Magazine，2007，24(4):118－121.

［12］许志强.压缩感知［J］.中国科学:数学，2012，42(9):865－877.

XU Zhiqiang.Compressed sensing:a survey［J］.Scientia Sinica Mathematica，2012，42(9):865－877.

［13］CHEN S，DONOHO D，SAUNDERSM.Atomic decomposition by basis pursuit［J］.SIAM Journal Scientific Computing，1999，20(1):33－61.

［14］TROPP J，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Trans on Information Theory，2007，53(12):4655－4666.

［15］BODIK P，WEIH，GUESTRIN C，et al.Intel Berkeley Lab WSN［EB/OL］.(2004－06－02)［2013－06－21］.http://db.csail.mit.edu/labdata/labdata.htm l.

(编辑:魏琴芳)