无人作战飞行器编队协同攻击轨迹规划研究

唐传林，黄长强，杜海文，黄汉桥，丁达理，罗畅

(空军工程大学 航空航天工程学院，陕西 西安710038)

0 引言

在未来军事应用领域，单无人作战飞行器(UCAV)作战将难以满足精确打击和时敏目标攻击的要求，UCAV 编队可对多个目标进行同时或依次攻击，提高对敌杀伤效果，与单UCAV 作战相比，具有协同感应、协同干扰、定时攻击、协同攻击、任务重新分配、提高生存概率等突出优点。因此，UCAV 编队协同作战成为世界各国研究的热点。攻击轨迹规划是UCAV 编队协同攻击的重要组成部分，直接影响任务的成败。

目前，关于UCAV 轨迹规划的研究文献很多，但大多都是将轨迹规划问题当作带约束的最优化问题［1-5］，没有考虑飞机的平台约束和运动特性，所得到的轨迹不具有可执行性。一些文献［6-9］对单机地形跟随、地面威胁因素以及多目标攻击进行了研究，但没有涉及多机协同。UCAV 编队作战相对于单机优势显著，同时为应对未来作战需求，研究编队协同攻击轨迹规划问题是很有必要的。

本文针对UCAV 编队协同攻击轨迹规划问题进行了研究，建立了编队的运动学/动力学模型，根据编队和单机约束条件，建立了编队轨迹规划模型，模型中目标函数的设计不仅考虑单机的威胁，还增加了编队等效碰撞次数和指令时间误差2 个目标子函数共同构成编队整体的目标函数。为使规划效果最优，将编队任务轨迹分段，采用hp 自适应伪谱法求解，并对结果进行了分析。

1 任务描述

编队协同攻击轨迹决策是指UCAV 在侦察到目标后，编队中的攻击机迅速机动到机载火控系统解算出的最佳武器投放位置，完成机动占位过程;编队中的其他飞机进入任务巡航轨迹，并在长机投放武器后，为武器提供目标信息直至武器命中目标，并进行毁伤评估的过程。假设由一架长机和一架僚机组成编队。长机负责攻击，僚机负责目标指示。如图1所示给出了编队协同作战的任务想定示意图。

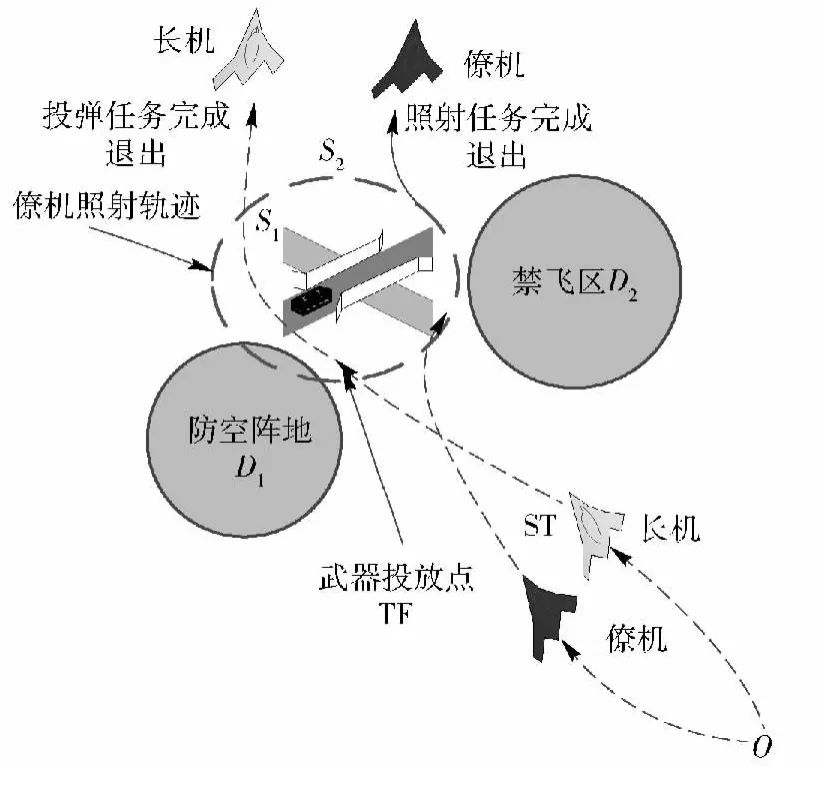
图1 编队协同作战任务描述Fig.1 Description of UCAV formation cooperative task operation

携带某型激光制导空地导弹的UCAV 编队从初始点O 开始按事先规划航迹在任务空域上侦察飞行。当机载探测系统发现目标及目标周围两处禁飞区D1、D2后(此时编队位于ST 位置)，编队控制中心根据当前作战需求发出打击指令。编队接收到作战指令后，轨迹规划模块依据火控系统解算的武器发射条件、平台状态和机动性能以及编队约束等各个约束条件，综合考虑攻击时间和威胁代价两方面因素，自动规划出编队成员的任务轨迹S1、S2. 具体地，当长机的攻击轨迹规划好以后，通过机间通信，将本机攻击轨迹数据、武器投放点位置、投放时间、投放角度、武器命中目标时间等信息通知僚机，僚机获取信息后，通过轨迹规划模块考虑攻击机轨迹、武器姿态信息、照射时间及地面威胁等因素，规划出照射任务轨迹。通过编队成员的协同，达到武器打击效能最优化的目的。任务完成后，编队退出战区。

2 UCAV 编队信息协同机制

编队的任务协同不仅包含了时间协同，还包含了载机姿态、速度、位置、目标照射角度等要素的协同。对UCAV 编队信息协同机制进行设计，如图2所示。

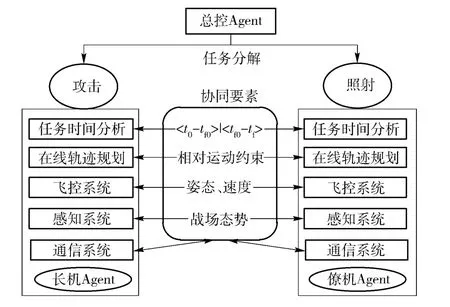
图2 编队协同要素Fig.2 Essentials for UCAV formation cooperation

在确定攻击目标后，控制中心根据目标信息和编队任务结构，将任务分解为攻击和照射2 个子任务，通过局域通信，发送给编队。长机根据接收到的攻击任务信息，结合本机特性进行任务分析，得出攻击任务所需时间T1= ＜t0～tf0＞，t0为长机攻击开始时刻，tf0为长机投放武器同时僚机照射目标，引导激光制导武器攻击目标的时刻。而后轨迹规划模块根据输入量T1，来自飞控系统的速度、姿态等参数及来自感知系统的两机相对位置、相对速度、相对角度等信息，快速规划输出最优攻击轨迹，最后通过通信系统将长机攻击时间T1、轨迹数据、武器参数、目标照射角度和照射时间等信息以数据包的形式发送给控制中心和僚机。

僚机在接收到控制中心和长机发送的信息后，根据照射时间T2= ＜tf0～tf＞，tf为武器命中目标的时刻。综合飞控系统、感知系统的数据作为轨迹规划模块的输入，进行快速规划，输出最优照射轨迹，然后通过通信系统将结果及相关数据信息发送给控制中心和长机。控制中心收到来自编队的反馈信息主要用来检测编队的空间运动约束及任务协同情况。

在执行任务过程中，编队将按固定时间间隔通过局域通信网与各个子系统进行信息交互以更新战场态势。

3 编队攻击轨迹规划数学模型

3.1 单机运动学/动力学模型

UCAV 模型采用质点模型

式中:(x，y，z)为UCAV 在地球坐标系中的位置;vUCAV为UCAV 的真空速;γ 为爬升角;ψa为航向角;α 为攻角;β 为侧滑角;μ 为速度滚转角;m 为UCAV的质量;g 为重力加速度;T =δTmax(vUCAV，h)为发动机推力，δ 为油门位置，Tmax为最大可用推力;分别为风速和风力加速度沿坐标轴的分量;和L =分别为阻力和升力;ρ 为空气密度;S 为参考面积;CL和CD分别为升力系数和阻力系数;c 为燃料消耗系数;P 为旋转角速度在气流坐标系的x 轴投影;Y 为侧力。

根据UCAV 飞行包线的约束，建立约束条件［7］

式中:mmin为安全返航所需最小燃油时的飞行器质量;Qmax为俯仰方向的最大角度变化率;Pmax(·)为当前迎角、马赫数和高度下滚转方向角度变化率;Ma(h(t)，v(t))为当前高度和速度下的马赫数;CL，max(α(t)，Ma(h(t)，v(t)))为当前迎角和马赫数下最大升力系数;nmax为UCAV 承受的最大法向过载;qmax为最大动压头;Hmin为最小安全高度。

UCAV 编队的轨迹还应该满足初始条件和满足武器投放的终端约束及目标照射角度的初始约束和终端约束。(4)式和(5)式为长机的初始条件和终端约束，(6)式～(8)式为僚机的轨迹初始、照射段和终端约束:

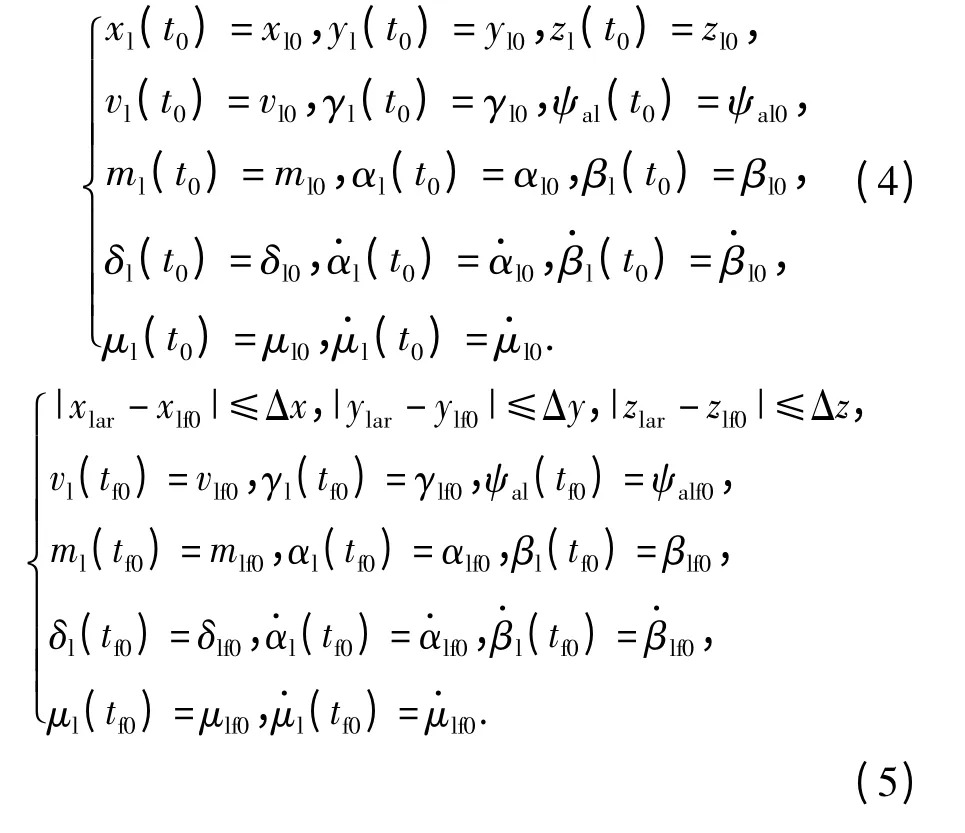
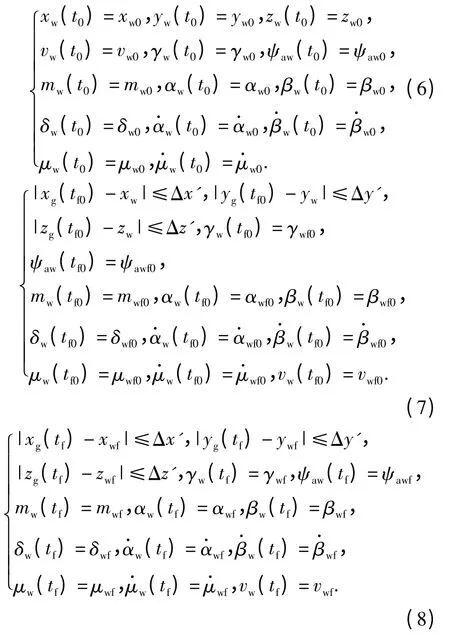
式中:下标l 表示长机;下标w 表示僚机;下标lar 表示投射区的指令位置;下标g 表示僚机任务开始的指令位置。

3.2 编队相对运动关系

如图3 所示给出了编队相对位置示意图。图中R 为相对距离。假设僚机处于编队最佳位置，忽略涡流等干扰因素对编队飞行控制的影响。文献［10］对飞机编队飞行控制进行了研究，建立了编队相对运动模型。本文所提出的模型

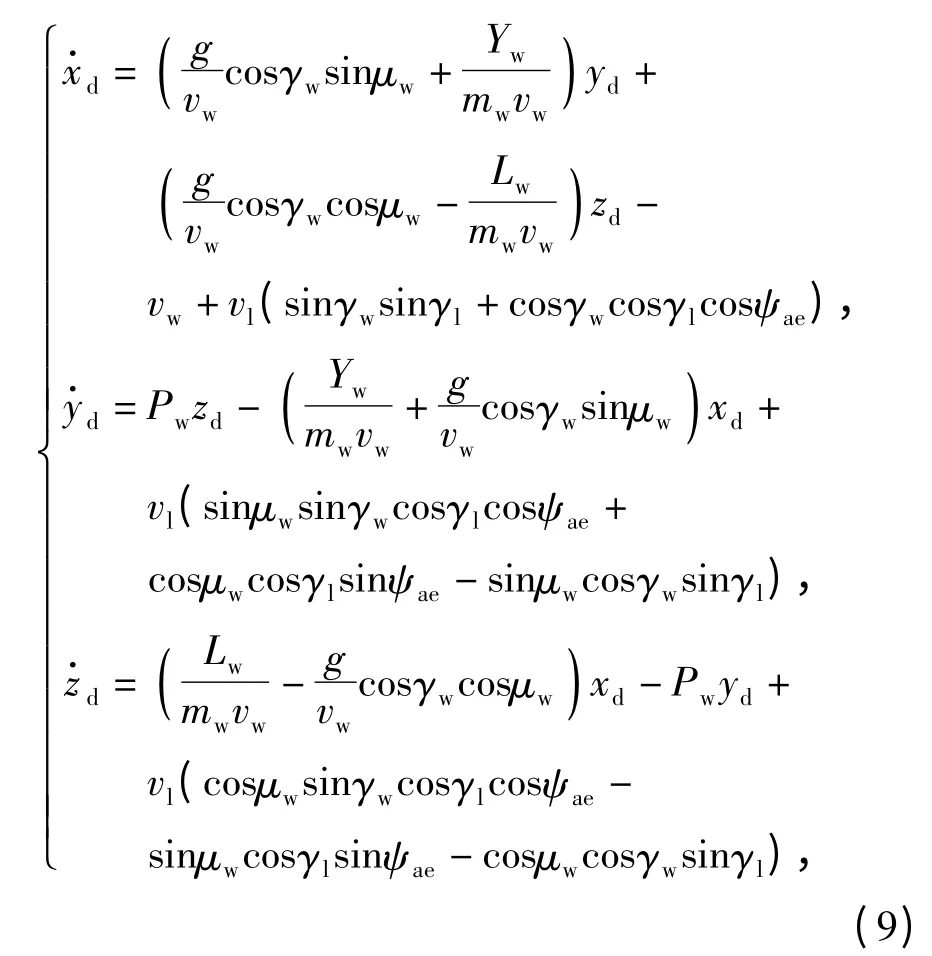
式中:xd，yd，zd和分别为长机与僚机相对距离及其变化率在僚机气流坐标系中的分量;ψae=ψal- ψaw为长机与僚机的航迹偏角差值;Yw=为侧力，CYβ为侧力系数，β 为侧滑角为僚机旋转角速度在速度坐标系x 轴的投影。

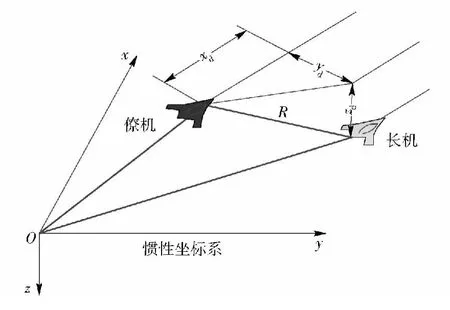
图3 编队成员相对位置Fig.3 Relative location among memberships

通过(1)式和(2)式分别列出长机和僚机的运动学/动力学模型并与(9)式联列，就建立了UCAV编队的数学模型。

3.3 威胁代价模型

3.3.1 地面威胁模型

现有的雷达和防空火力威胁模型都比较成熟，为方便计算提出威胁矢量的概念。

定义 相对于UCAV，不同位置处威胁的矢量表示形式即为威胁矢量。

对于雷达威胁，UCAV 在某一位置的被探测概率与飞机当前相对雷达的姿态及距离有关;对于防空火力，UCAV 在某一位置被毁伤的概率与飞机当前对防空火力的距离和飞行速度有关。如图4 所示，威胁矢量形式为

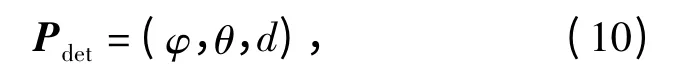
式中:φ 为威胁源与飞机连线在惯性坐标系平面中的投影相对于y 轴的夹角，逆时针方向为正;θ 为威胁源与飞机连线相对于惯性坐标系平面的夹角，向上为正;d 为威胁源与飞机之间的距离。

UCAV 在特定位置处的总威胁，可用矢量和形式表示

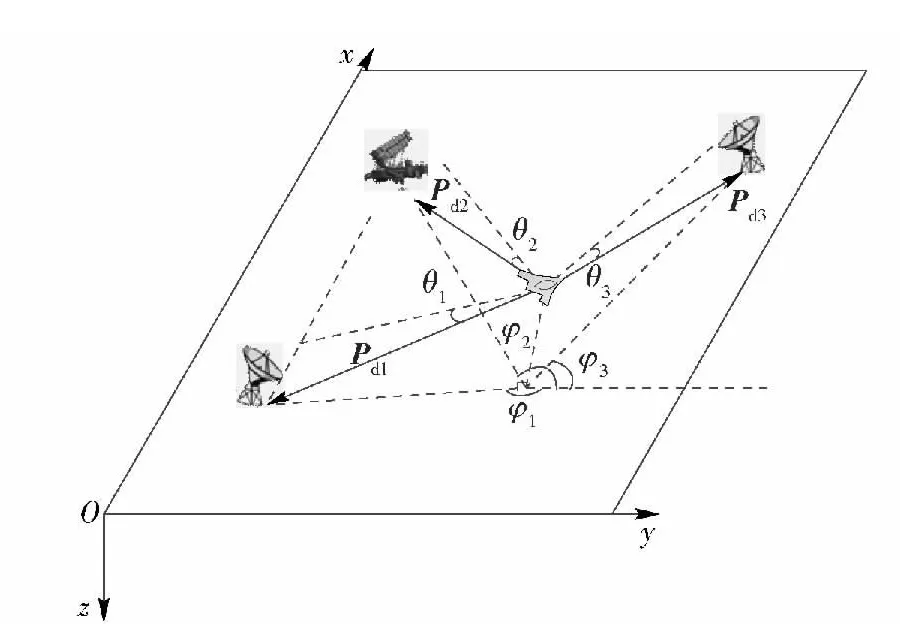
图4 威胁矢量示意图Fig.4 Schematic diagram of threat vector

威胁值大小要根据具体威胁类型计算，由于现代防空火力都是由地空导弹和防空雷达组成的联合防空系统，故本文将雷达和防空火力的威胁统称为地面防空威胁，对于具有n 个子系统的联合防空系统的探测威胁，Pdet为探测概率矢量，于是联合防空系统探测概率大小为

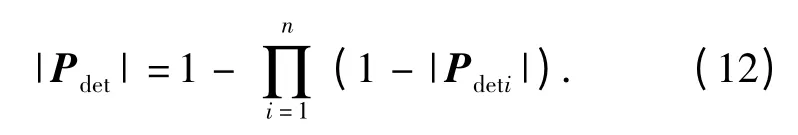
式中:|Pdeti|为第i 部联合防空子系统探测概率大小，其计算方法参考文献［8］.

3.3.2 空中威胁模型

由于是编队协同作战，空中威胁主要来自编队内部，因此考虑编队成员的飞行安全是有必要的。文献［11］对UAV 编队成员间的碰撞及规避问题进行了详细研究。文中考虑2 种情形:1)同向飞行时，为了保持编队的构型，故在飞行相对距离、速度、角度等方面加以限制;2)其他方向飞行时，不考虑编队构型，只要求相对高度大于安全相对高度。根据所建立的编队相对运动数学模型，将防撞模型转化为对成员间相对距离、速度、角度的约束条件如下:

3.4 目标函数

编队轨迹的目标函数不仅包括单机的威胁代价，还包括编队成员间的碰撞代价以及协同时间代价。因此，对于单机的目标函数，本文采用文献［8］提出的目标函数;对于编队成员间的代价，建立目标函数

对于时间协同代价，建立目标函数

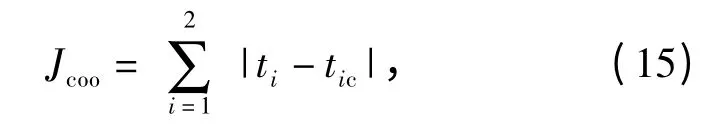
式中:ti为UCAV 达到指定位置的实际时间;tic为UCAV 到达指定位置的指令时间。

综合以上对编队目标函数的分析，采用加权性能指标作为编队目标函数，在实际应用中依据战场需要，确定权重系数。综合目标函数表示为

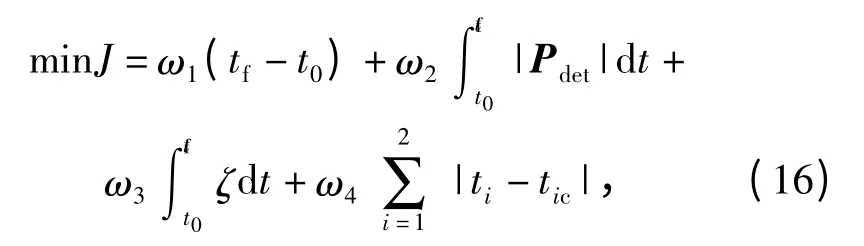
式中:ω1、ω2、ω3、ω4四项分指标分别为时间最短、威胁最小、等效碰撞次数最少、指令时间误差最小，且ω1+ω2+ω3+ω4=1.

4 最优轨迹求解策略

4.1 求解框架

目前常用的路径规划算法包括整数规划方法、动态规划方法、群智能算法、进化算法、最优控制等多种方法，这些方法各有优劣，由于本文所规划的飞行航迹包含了飞行运动学和动力学约束，因此最优控制方法是求解此类问题的最为合适的框架。

根据最优控制理论，UCAV 状态变量和控制变量分别为

迈耶尔型性能指标为(对应(16)式)

动力学微分方程约束(对应(1)式、(2)式、(9)式)

边界条件(对应(4)式～(8)式)

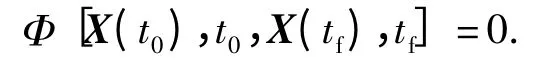
不等式约束(对应(3)式、(13)式)

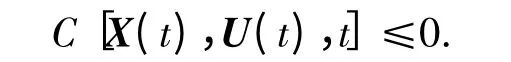
4.2 基于hp 自适应伪谱法的轨迹优化算法

最优控制问题求解方法分为直接法和间接法2 种类型。全局伪谱法作为直接法中发展较为迅速的一个分支，可运用较少的节点获得较高精度的解，但在求解大规模复杂问题时效果不理想。考虑到文中编队轨迹规划问题约束条件多，变量之间存在耦合，因此采用hp 自适应伪谱法［12-14］，该方法汲取了全局伪谱法与有限元的优点，采用双层策略对最优控制问题进行求解，与全局伪谱法相比，计算占用时间少，精度高。算法的描述及具体解算过程参考文献［13］.

4.3 轨迹分段优化

由于本文任务设定为长机执行投弹攻击任务，僚机执行照射目标为激光制导导弹提供目标指示任务。因此在tf0时刻长机攻击任务执行完毕，攻击轨迹对应的时间段为t0～tf0，在此时间段内僚机没有任务;从tf0时刻起僚机开始执行照射任务，起止时间为tf0～tf，而在此时间段内，长机没有任务。如果任务要求编队在完成任务后，自行离开战区，则长机先于僚机退出;如果任务要求编队在完成任务后，仍以编队共同离开，则长机应等待僚机完成任务。为优化编队攻击轨迹，文中提出以任务执行节点为界限，将任务轨迹分段进行优化，分为巡航段、任务段和撤出段。对于自行离开的情形，编队只需要求僚机在武器投放时刻tf0到达指定位置即可;对于同时离开的情形，需考虑等待编队成员完成任务并确保自身安全，情况更复杂，分段示意图如图5 所示。

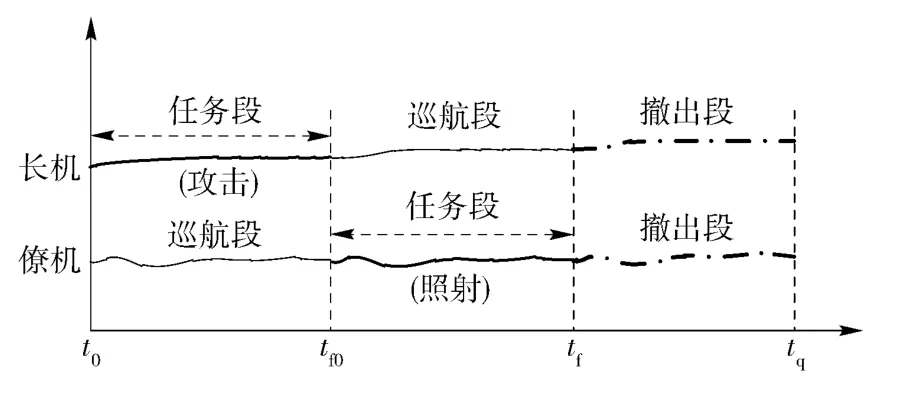
图5 轨迹分段Fig.5 Trajectory subsection

将任务轨迹分为3 段，用hp 自适应伪谱法对每段求解，并注意使各段相连的端点的状态一致，保证轨迹平滑连接，所得到的任务轨迹比不分段的情形结果更好。

5 仿真结果及分析

假设UCAV 编队在位置(20 km，20 km，0 km)处发现一个恐怖份子活动场所，类型为地面固定目标;在位置(10 km，20 km，0 km)和(23 km，15 km，0 km)发现雷达和防空导弹阵地，目标类型为地面固定威胁。UCAV 部分参数如表1 所示。侧滑角范围假设为［-20°，20°］，侧滑角角速率范围为［-10°/s，10°/s］. 威胁参数参考文献［8］，其余仿真参数如表2 所示。假设武器为某型半主动激光制导导弹，其质量为300 kg，飞行速度为360 m/s，投放时的姿态与载机脱离瞬间的姿态相同。目标函数的加权系数设置为ω1=ω2=ω3=ω4=0.25.

表1 UCAV 仿真模型参数Tab.1 Parameter values for UCAV simulation model

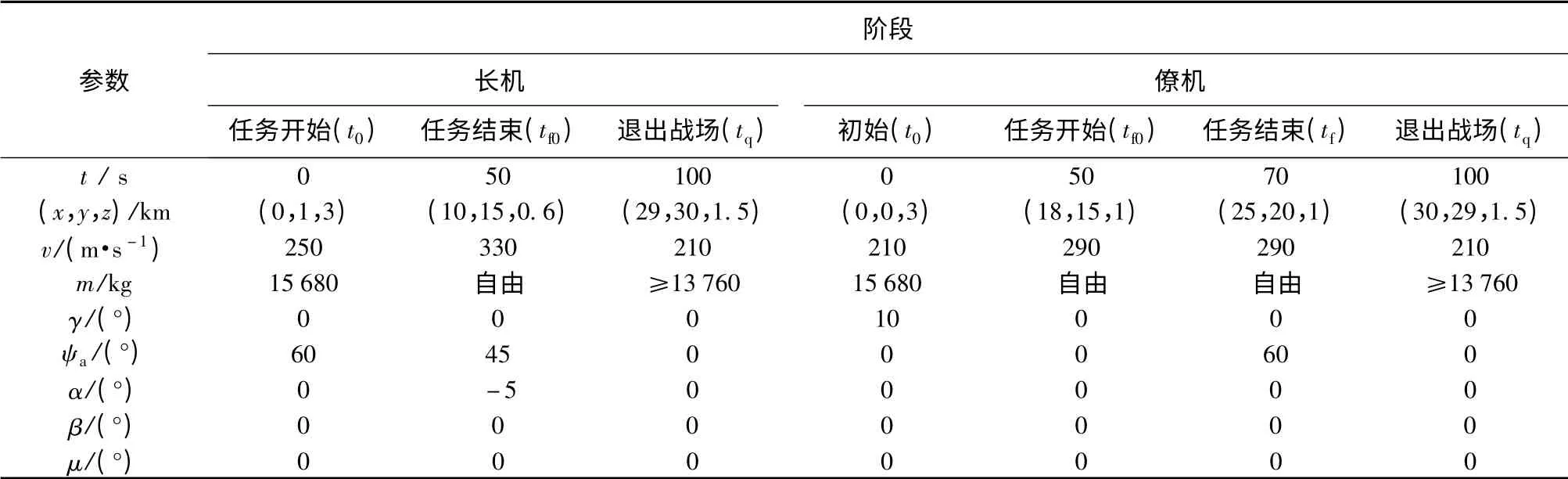
表2 仿真参数Tab.2 Parameter values for simulation

如图6 所示为编队成员间相对距离。

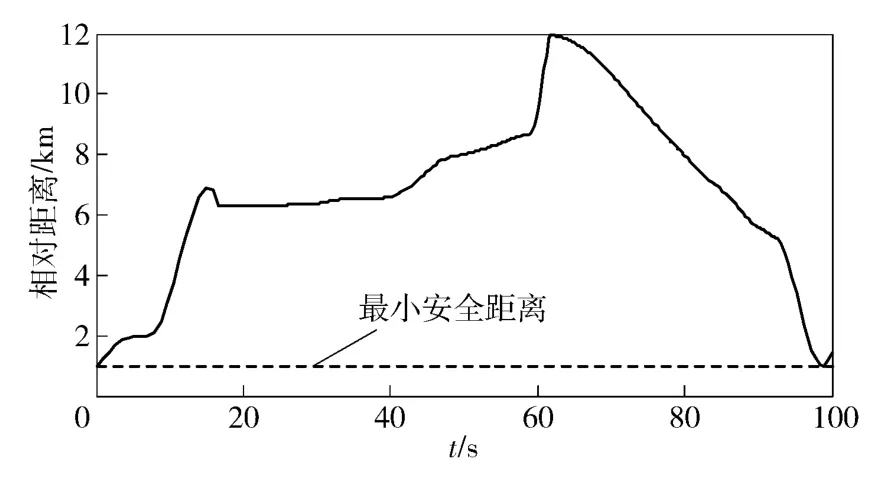
图6 相对距离随时间变化曲线Fig.6 Relative distance vs. time

由图6 可看出，所规划的轨迹满足不碰撞的约束条件，即等效碰撞次数为0;值得注意的是在59 ～62 s 时间段内相对距离变化剧烈，这是由于长机在第50 s 发射导弹后，此后快速脱离攻击区，以寻求自身安全。仿真结果图中各个状态量用不同时间段表示:0 ～50 s 为第1 段，对应50 s ～70 s 为第2 段，对应70 s ～100 s 为第3 段。

如图7 所示为编队二维平面轨迹和三维空间轨迹。

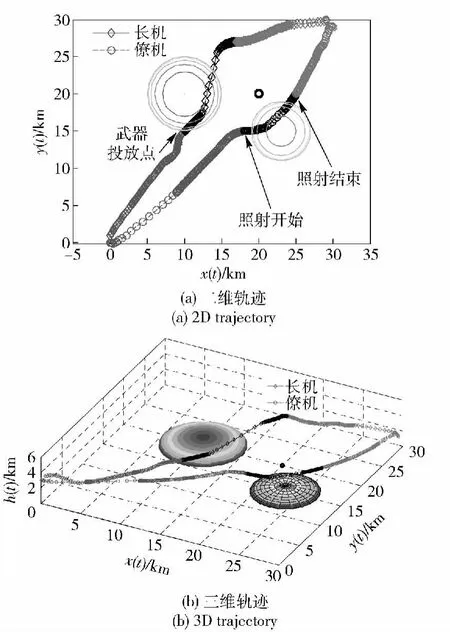
图7 编队轨迹Fig.7 UCAV formation trajectory

由图7 可看出:长机在(10 km，15 km，0.6 km)处发射武器后快速脱离，以避免进入威胁区;根据仿真设置的协同要素约束，僚机此时进入任务位置(18 km，15 km，1 km)，开始对目标进行照射并保持恒定高度直至任务结束僚机此刻位于(25 km，20 km，1 km);可看出所规划的轨迹比较光滑，能够自然地衔接各个任务段。

如图8 所示为编队状态变量随时间的变化曲线。

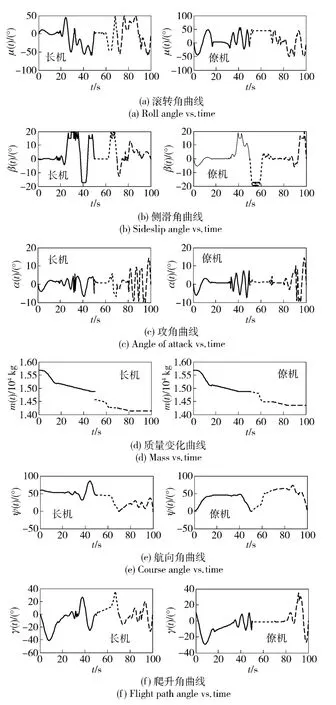
图8 编队状态参数变化曲线Fig.8 UCAV formation state parameters vs. time

由图8 可知，在规划的整个飞行轨迹中，编队的状态量都保持在设定的范围内，飞行姿态能够满足所有设定的机动性能约束，任务所要求的姿态协同的约束条件也能够满足。注意图8(d)中长机质量变化曲线在50 s 时出现落差，质量突然减少，是由于长机此刻投放武器。经解算求得目标函数值为61.438 4. 整个规划时间为249.57 s，规划时间较长，原因在于:1)编队规划问题约束条件多，所建立的数学模型维数大;2)采用的算法计算效率不足导致的。

6 结论

本文研究了UCAV 编队协同对地攻击轨迹规划问题，从仿真结果看:建立的双机编队轨迹规划数学模型是合理的，通过仿真验证了有效性;对整个轨迹按照任务进行分段，并采用hp 自适应伪谱法进行解算，能够得到编队的最优攻击轨迹，且满足给定的约束条件;建立的数学模型维数大，规划时间长，不适合在线规划。进一步的研究重点将放在对模型和算法的改进上，寻求满足在线要求的规划方法。

References)

［1］苏菲，彭辉，沈林成. 基于协进化多子群蚁群算法的多无人作战飞机协同航迹规划研究［J］. 兵工学报，2009，30(11):1562 -1568.SU Fei，PENG Hui，SHEN Lin-cheng. Research on multi-UCAV cooperative route planning based on coevolutionary multi-antcolony algorithm［J］. Acta Armamentarii，2009，30(11):1562-1568. (in Chinese)

［2］孙阳光，丁明跃，周成平，等. 基于量子遗传算法的无人飞行器航迹规划［J］.宇航学报，2010，31(3):648 -654.SUN Yang-guang，DING Ming-yue，ZHOU Cheng-ping，et al.Route planning based on quantum genetic algorithm for UAVs［J］. Journal of Astronautics，2010，31 (3):648 - 654. (in Chinese)

［3］陈海，王新民，焦裕松，等. 一种凸多边形区域的无人机覆盖航迹规划算法［J］.航空学报，2010，31(9):1802 -1808.CHEN Hai，WANG Xin-min，JIAO Yu-song，et al. An algorithm of coverage flight path planning for UAVs in convex polygon areas［J］. Acta Aeronautica et Astronautica Sinica，2010，31(9):1802-1808.(in Chinese)

［4］何平川，戴树岭. 一种改进的UAV 三维航迹实时规划算法［J］.北京航空航天大学学报，2010，36(10):1248 -1251.HE Ping-chuan，DAI Shu-ling. Improved 3D real-time trajectory planning algorithm for UAV［J］. Journal of Beijing University of Aeronautics and Astronautics，2010，36(10):1248 -1251. (in Chinese)

［5］姚远，周兴社，张凯龙，等. 基于稀疏A*搜索和改进人工势场的无人机动态航迹规划［J］. 控制理论与应用，2010，27(7):953 -959.YAO Yuan，ZHOU Xing-she，ZHANG Kai-long，et al. Dynamic trajectory planning for unmanned aerial vehicle based on sparse A*search and improved artificial potential field ［J］. Control Theory ＆ Applications，2010，27(7):953 -959. (in Chinese)

［6］Williams P. Aircraft Trajectory planning for terrain following incorporating actuator constraints［J］. Journal of Aircraft，2005，42(5):1358 -1361.

［7］刘鹤鸣，黄长强，黄汉桥，等.快速避障三维最优轨迹规划研究［J］.电光与控制，2013，20(3):1 -5.LIU He-ming，HUANG Chang-qiang，HUANG Han-qiao，et al.Fast and optimal three dimensional trajectory planning with obstacle avoidance performance ［J］. Electronics Optics ＆Control，2013，20(3):1 -5. (in Chinese)

［8］刘鹤鸣，丁达理，黄长强，等.基于自适应伪谱法的UCAV 低可探测攻击轨迹规划研究［J］. 系统工程与电子技术，2013，35(1):79 -81.LIU He-ming，DING Da-li，HUANG Chang-qiang，et al. UCAV low observable attacking trajectory planning based on adaptive pseudospectral method［J］. Systems Engineering and Electronics，2013，35(1):79 -81. (in Chinese)

［9］张煜，陈璟，沈林成. UCAV 空面多目标攻击三维轨迹规划技术［J］.国防科技大学学报，2012，34(5):107 -114.ZHANG Yu，CHEN Jing，SHEN Lin-cheng. 3-dimensional trajectory planning for single UCAV attacking multiple targets［J］.Journal of National University of Defense Technology，2012，34(5):107 -114. (in Chinese)

［10］Osteroos R K，Pachter M，Jacques D R. Full capability formation flight control［C］∥AIAA Guidance，Navigation，and Control Conference. Rhode Island:AIAA，2004:1 -15.

［11］Désilles A，Zidani H. Collision analysis for an UAV［C］∥AIAA Guidance，Navigation，and Control Conference. Minneapolis:AIAA，2012:1 -23.

［12］Rao A V. A survey of numerical methods for optimal control［J］.Advances in the Astronautical Sciences，2009，135(1):497 -528.

［13］Darby C L， Hager W W， Rao A V. An hp-adaptive pseudospectral method for solving optimal control problems［J］.Optimal Control Applications and Methods，2011，32(4):476-502.

［14］HONG Bei，XIN Wan-qing. Rapid gliding trajectory optimization via hp-adaptive pseudospectral method［C］∥Proceedings of the 30th Chinese Control Conference. Yantai:IEEE，2011:1956 -1961.