TNT 装药渗出过程的数值模拟

孟祥尧，邱志明，，张鹏，韩守鹏，宋保维

(1. 西北工业大学 航海学院，陕西 西安710072;2. 海军装备研究院，北京100073)

0 引言

隐藏爆炸物的探测和清除是当前的国际性难题，一直倍受各国关注。在各种爆炸物探测方法中，化学痕量探测是近年来发展的新型探测方法，比较常用的有离子迁移谱法、荧光分析法、电化学法、表面声波法等［1-2］。由于其灵敏度高、识别性强等优点，而越来越受到人们的青睐。可供探测方法检测的炸药成分主要来源于表面残留、泄漏和渗出，其中渗出是影响化学痕量探测的关键过程，渗出的量和速率越大，越容易被探测到;且炸药成分的渗出与其在周围环境中的传播、变化或反应［1］都有很大关系，直接影响最后可检测到的化学物质的种类及数量。因此，深入了解和研究爆炸物装药渗出过程非常必要，对爆炸物化学痕量探测系统的设计研究具有指导意义。

目前，只有部分国外文献［2-5］对一些陆上爆炸物的装药渗出过程进行了实验测量和分析，但因爆炸物种类繁多及实验条件的限制，进行实验研究比较困难，所以为进一步了解装药渗出过程及在无法进行实验时获得所需数据，就必须进行理论分析以弥补实验的不足。目前尚未有针对此方面的理论研究，本文目的在于建立合理的数学模型来描述并进一步分析炸药渗出过程。爆炸物装药的包覆材料一般为金属或聚合物，但金属材料中炸药分子很难渗出，因此渗出多发生在聚合物材料的壳体和密封件处，本文针对炸药在聚合物材料中的渗透进行理论分析研究和数值模拟计算，可以在无法得到实测数据的情况下，为研究爆炸物化学痕量探测提供炸药渗出的相关数据，以促进发展更有效的隐蔽爆炸物探测系统。

1 爆炸物装药渗出模型

1.1 爆炸物装药的渗出机理

装药渗出的微观过程为溶解—扩散—解吸。炸药产生的气体首先吸附并溶解于材料中，然后在浓度差的推动下通过孔穴或分子间的空隙向低浓度的地方扩散，最后通过解吸从材料的外表面脱离到环境中。如图1 所示整个渗出过程的简化示意图。炸药通过一定面积的平板渗透出来，外部环境为水、空气或土壤等，图中阴影部分为爆炸物壳体结构。外部环境中的水或空气都有一定的流动速度而非静止的。

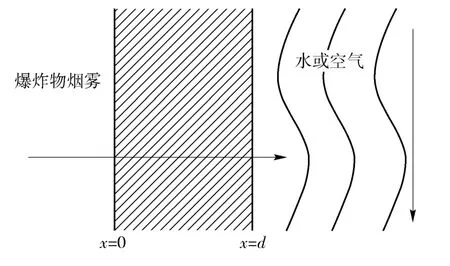
图1 渗透过程简化模型Fig.1 Simplified model of the leakage process

化学物质在聚合物中的扩散速率由扩散系数决定，扩散系数越大，物质在材料中的扩散速率越快。溶解在聚合物中的化学物质的量叫做溶解度，溶解度越大，相应的渗出就会越明显。

1.2 扩散方程

渗出过程中炸药分子的扩散过程是非稳态的，一维平板情形下，扩散服从Fick 第二定律:

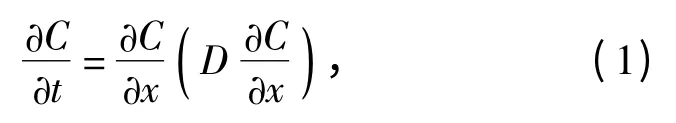
式中:D 为扩散系数;C 为扩散分子的浓度。

若在圆柱中沿径向扩散，则扩散方程变为

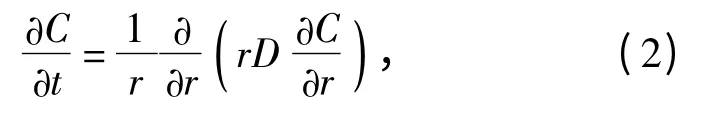
式中:r 为圆柱半径。球体中的扩散等其他情形都可根据(1)式在不同坐标系下的展开得到。

1.3 初始条件

初始条件C=C0(0 ＜x ＜d，t=0)为初始时刻聚合物材料中炸药分子的分布情况。一般认为C0=0，但也可能是非零常数或其他函数形式f(x)，具体问题需根据实际情况来确定。

1.4 边界条件

渗出过程中，溶解和解吸2 个过程通过边界条件进行描述。由图1 知，在x =0 的一侧，一般认为炸药分子在聚合物表面的浓度为其在聚合物中的溶解度，也即C =C1(x =0，t ＞0)，其中C1为溶解度。若已知炸药分子在聚合物中的溶解系数S，则可根据亨利定律得到聚合物表面浓度C1，表达式为

式中:p1为炸药在一定温度下产生的含炸药成分的气体分压。

在x=d 处，炸药分子通过两相界面解吸而释放到周围环境中。两相间的传质可使用双膜传质理论、溶质渗透理论和表面更新理论等进行描述。其中，双膜传质理论简洁直观，较其他2 种理论更容易得到相关参数，因此本文采用双膜传质理论来描述相际传质。双膜模型的示意图如图2 所示。

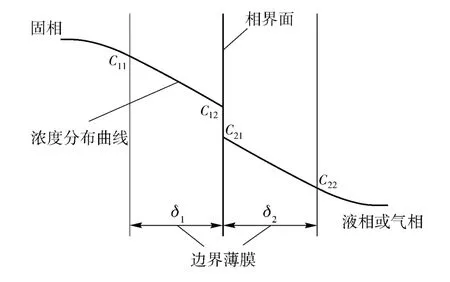
图2 双膜传质模型Fig.2 Model of the two-film mass transfer

由图2 可看出，双膜理论假设在相界面两侧存在2 个边界薄膜，物质从一相进入另一相的传质过程中的阻力集中在界面两侧的膜内;在相界面上，物质的交换处于动态平衡;边界膜内的相是静止不动的，不受外部流动相的影响;膜内通过分子扩散实现质量传递，并且认为质量传递过程是定态的。

炸药分子由固相主体传递到固相边界膜内并扩散至相界面时，在相界面上立刻达到平衡，然后通过液相或气相的边界膜扩散，到达液相或气相主体。在两层膜内，根据双膜理论，每一相的传质分系数与传递组分在该相中的分子扩散系数成正比，与膜的厚度成反比。相际传质的总阻力等于两相传质的分阻力之和。

下面给出x=d 处边界条件的推导过程。

在描述相界面两侧的边界膜厚度时，因为在整个材料中炸药分子的扩散都满足Fick 定律，故本文选择材料的厚度作为固相边界膜的厚度;而在液相或气相一侧，存在液体的流动，假设其在一定范围内为层流，则膜厚度可以根据有效边界层厚度公式获得［7］:

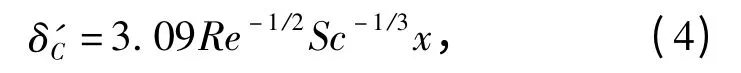
式中:Re 为雷诺数;Sc 为施密特数;x 为与板端的距离，假设其为特征长度(平板长度)的1/2，以此处的有效边界层厚度作为整个平板的平均边界层厚度。

在液固相界面的动态平衡中有平衡常数

式中:Sl和Ss分别为炸药在液体和固体中的溶解度，当相为气体时同理。

根据双膜理论的假设及图2，在相界面两侧的边界膜内满足Fick 定律，并且相界面两侧的通量是相同的，因此有

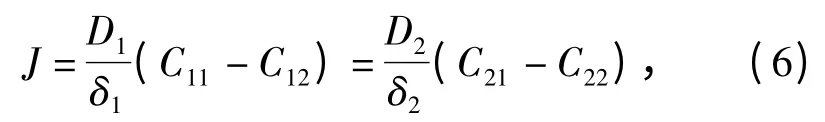
式中:D1和D2分别为炸药分子在固体和液体(或气体)中的扩散系数;δ1和δ2分别为固相膜和液相膜(或气相膜)的厚度;Cij(i=1，2;j=1，2)为图中相应位置的炸药分子浓度。

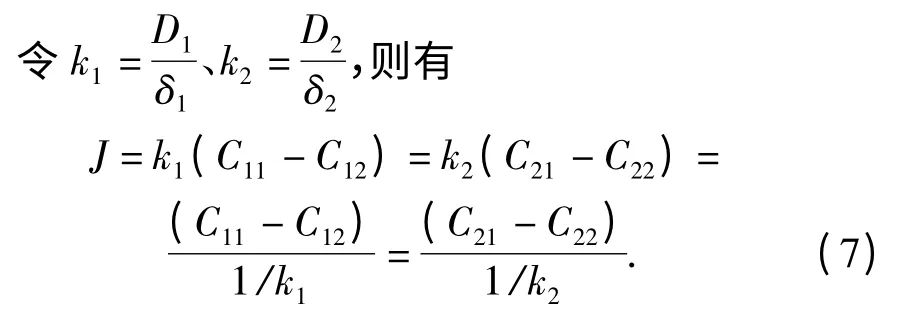
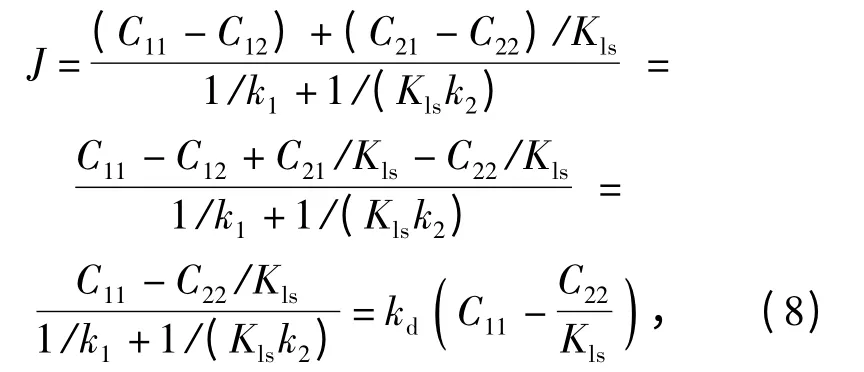
根据以上分析，在解吸的一侧有以下边界条件:

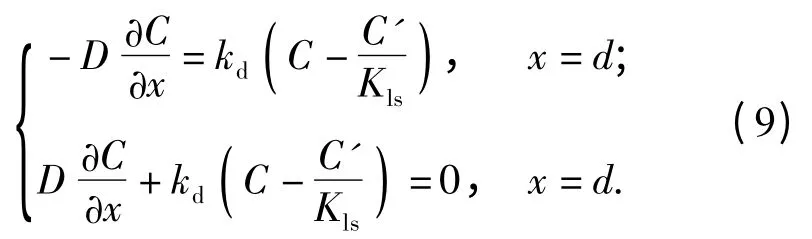
式中:C'为外部环境中炸药分子的浓度。

通过上述分析，最终得到渗出的数学模型为

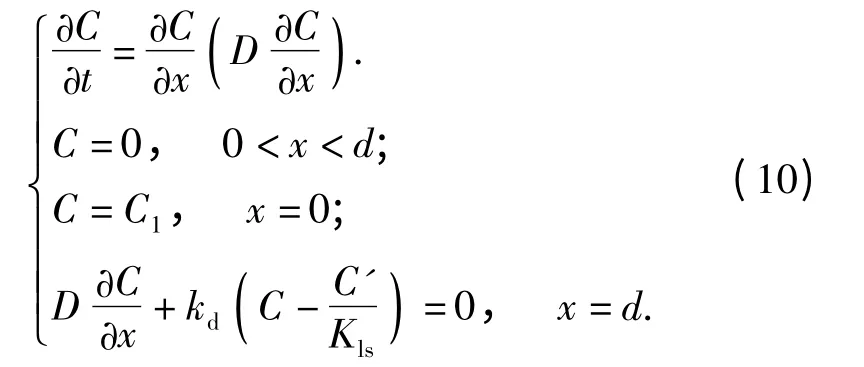
2 算例及分析

对于外壳为金属的爆炸物，炸药分子只能从橡胶材料的密封件处渗出，针对TNT 透过厚度d =0.32 cm 橡胶平板渗出到水中的情况进行计算，如图1 所示。假设初始浓度分布为0，而由于水的流动，认为外部环境中的炸药分子浓度也为0. 其他参数［2-4］:橡胶中TNT 的扩散系数Ds=10-7g/cm3，橡胶中TNT 的溶解度Ss=1.3 ×10-3g/cm3，传质系数kd 由计算得到，水中TNT 的扩散系数Dl=1.18 ×10-5cm2/s，水中TNT 的溶解度Sl=1.3×10-4g/cm3，水的流速vl=1 cm/s.

根据(10)式，使用Matlab 中的PDE 相关函数进行求解，得到了不同时刻下平板内浓度随位置的变化曲线，如图3 所示。

由图3 可以看出浓度分布随时间(单位:s)和位置的变化，x 为平板中的位置如图1 所示。随着时间的增加，浓度分布逐渐趋于稳定的线性分布，并最终达到稳定状态。在x 值较小的位置，浓度较高;随着x 的增大浓度减小。随着时间的不断发展，橡胶平板x=d 界面处浓度不为0，并逐渐趋向于一个稳定常值。这是因为相际间存在传质阻力，使得橡胶内炸药分子在x =d 处不能直接扩散到周围环境中，而产生积累，直到到达稳定状态。

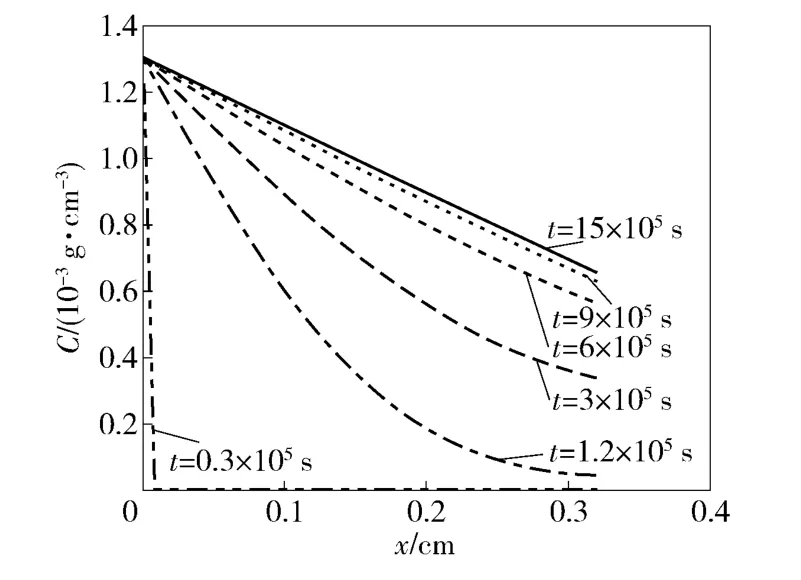
图3 不同时刻下TNT 浓度随距离x 的变化关系Fig.3 Change of TNT concentration with distance x at different time

如图4 所示，给出了x =d 处，也即与水接触处的扩散通量。随着时间的增加，扩散通量从0 开始逐渐增大，最后趋于稳定，所需时间大约2 个星期左右。具体计算结果如表1 所示。

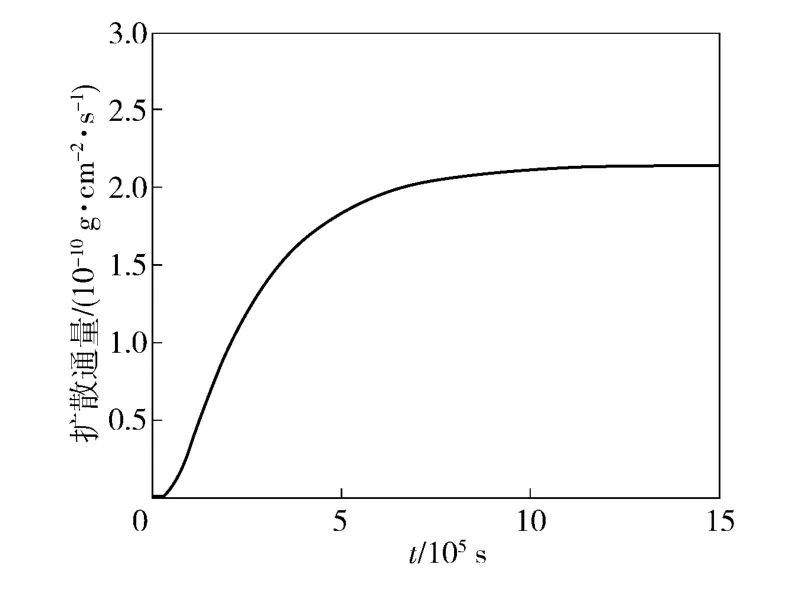
图4 x=d 处不同时刻的扩散通量Fig.4 Diffusion flux at different times for x=d

表1 计算结果与实验结果的对比Tab.1 Comparison of calculated and experimental results

由表1 可看出，利用本文模型计算出的扩散通量与实验结果在数量级上是一致的，这很好地验证模型的合理性。另外，由于对某些影响因素的省略、应用理论模型的简化及实际环境因素的影响等等原因，模型与实验结果是必然存在差异的，但由于扩散通量量级很小，所存在的误差在可接受的范围内。

影响扩散通量的因素比较多，如材料种类、扩散系数、材料厚度等，在同种材料中由于扩散系数相同，材料厚度对扩散通量的影响最大。如图5 所示，通过文中建立的模型计算不同材料厚度的扩散通量，可清晰地看出厚度对扩散通量的影响，厚度越大，稳定后扩散通量越小，并且达到稳定所需的时间越长。换而言之，随着厚度的增加，渗透扩散变得困难。

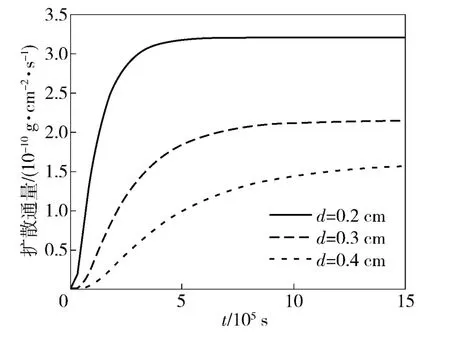
图5 不同厚度d 下扩散通量随时间的变化曲线Fig.5 Change of diffusion flux with time at different thickness d

当外部环境为空气时，同样可以利用文中所建立的模型进行计算。此时，其他条件不变，相关参数:空气中TNT 的扩散系数Dg=6.44 ×10-2cm2/s，空气的流速vg=1 cm/s，20 ℃TNT 的饱和气体密度Sg=4.35 ×10-11g/cm3.

通过计算所得结果如表2 所示。

表2 计算结果与实验结果的对比Tab.2 Comparison of the calculated and experimental results

由表1 和表2 可得:外部环境为水或空气时，爆炸物的扩散通量分别为2.1 × 10-10g/(cm2·s)、1.4 ×10-12g/(cm2·s). 2 种情况下炸药分子在橡胶内的溶解系数和扩散系数是相同的，故导致扩散通量不相等的原因为爆炸物与空气和与水接触时的解吸速率不相等。与水接触时的扩散通量比与空气接触时大，说明在水中的解吸速率更快，炸药分子在水中比在空气中更容易渗透出来。利用文中模型所得的计算结果与文献［8］实验结果是一致的。另外相对于爆炸物炸药分子在水中的渗出，在空气中的渗出在稳定后的扩散通量较小，达到稳定所需的时间更长。这说明在相际界面并不是直接进行炸药分子的传递，而是受到了一定的阻碍，并且外部环境不同时，阻力不同，爆炸物在空气中时，炸药分子渗出的阻力较大，这与文献［6］中炸药分子在水中更易渗透出来的实验结果也保持一致，进一步说明了本文模型的合理性和有效性。

3 结论

本文通过建立爆炸物装药渗出过程的数学模型，对TNT 通过橡胶材料的渗透过程进行了数值模拟。分析了TNT 在渗出过程中的浓度分布，得到了在水和空气中TNT 通过橡胶的扩散通量，得出了厚度的增加会使渗透扩散变得困难以及炸药分子在水中比在空气中更容易渗透出来的结论。仿真结果与文献中的实验结果保持一致，验证了模型的合理性。利用本文模型可以快速而有效地获得TNT 渗出过程的理论数据，但还需在具备条件时通过各种算例及实验数据对理论模型进行进一步的检验和优化。

References)

［1］丁文，窦玉玲，王国保，等. 爆炸物的探测技术综述［J］. 爆破器材，2011，4(5):33 -37.DING Wen，DOU Yu-ling，WANG Guo-bao，et al. Review on detection technology for explosives［J］. Explosive Materials，2011，4(5):33 -37. (in Chinese)

［2］Woodfin R L. Trace chemical sensing of explosives［M］. New Jersey:John Wiley ＆ Sons，2007.

［3］Phelan J M，Barnet J L，McConnell P E. Explosive signature flux from field recovered landmines， SAND2004-3913 ［R］.Albuquerque:Sandia National Laboratories，2004.

［4］Leggett D C，Cragin J H，Jenkins T F，et al. Release of explosive-related vapors from landmines，ERDC/CRREL TR-01-6［R］. US:Engineer Research and Development Center Hanover NH Cold Regions Research and Engineering Lab，2001.

［5］Cragin J H，Leggett D C. Diffusion and flux of explosive-related compounds in plastic mine surrogates，ERDC/CRREL TR-03-12［R］. US:Engineer Research and Development Center Hanover NH Cold Regions Research and Engineering Lab，2003.

［6］Phelan J M，Barnett J L，Romero J V，et al. Explosive chemical emissions from landmines［C］∥Proceedings of SPIE. Orlando :SPIE，2003:746 -754.

［7］沈巧珍，杜建明. 冶金传输原理［M］. 北京:冶金工业出版社，2006.SHEN Qiao-zhen，DU Jian-ming. Metallurgy transport principle［M］. Beijing:Metallurgical Industry Press，2006. (in Chinese)

［8］Tung Y S，Henderson D O，Curby W A，et al. Diffusion kinetics of TNT in acrylonitrile-butadiene rubber via FT-IR/ATR spectroscopy［J］. Applied Spectroscopy，1997，51(2):174 -177.

［9］McLean I G. Mine detection dogs:training，operations and odour detection［M］. Geneva:GICHD，2003.

［10］Phelan J M，Barnett J L. Solubility of 2，4-dinitrotoluene and 2，4，6-trinitrotoluene in water［J］. Journal of Chemical ＆Engineering Data，2001，46(2):375 -376.