基于模糊需求的复杂物流库存系统模型分析

吴维德,白 泰,罗银康,向景睿,金 鑫

（四川省电力公司计量中心,四川成都,610072）

基于模糊需求的复杂物流库存系统模型分析

吴维德,白 泰,罗银康,向景睿,金 鑫

（四川省电力公司计量中心,四川成都,610072）

物流系统中供需方关系的动态变化性符合复杂系统范畴，对于复杂物流系统中不确定性需求求解本文采用模糊集合方法，构建基于模糊需求的库存模型，对分散控制与部分调控策略下零售商、批发商与供应商最佳订货点量进行分析，并通过实例对构建的模型有效性进行验证。

模糊需求；复杂物流系统；库存模型

0 引言

国内物流系统研究起步较晚，在研究理念与研究方法、手段上与国外有一定的差距，目前国内物流领域的研究聚集在物流设备、技术及产业三方面，计算机仿真方面的研究也逐渐增多。可以看出物流研究的技术手段在加强，研究的范围在拓宽，但是，对于物流系统中具体的业务关系研究还是比较欠缺，大量的研究都集中在库存-路径、线路规划上，对供需关系中不确定性需求影响库存方面涉猎不足，因此，本文以此为切入点，引入模糊方法，基于模糊需求对物流系统中库存问题进行研究。

1 复杂物流系统

1.1 不确定性

不确定性是指事物的无序的、模糊的一种属性，物流系统的不确定性是指物流供应链中动态变化的供需关系造成了各方不便，增加了管理难度。物流系统的不确定性可以分为三方面：供应不确定性、制造与需求不确定性。

1.2 模糊方法的应用

模糊理论要解决的问题即不确定的，无法准确描述的，需要用一个集合来表示，将该问题所有的解囊括在集合中，并建立一个与该集合对应的区间（0到1）与之对应，前者称为模糊集合即解的集合，后者称为隶属度，两者间的映射即为隶属函数，模糊理论便是运用隶属度函数变化过程来定量化地刻画问题解的趋势，给出一个近似准确的解。

对于物流系统而言，从其不确定的描述可以获知客户需求变化不定，零售商、供应商、生产商均不能准确制定需求计划，运用传统的概率统计法需要大量历史数据，不是最佳方法，企业一般会主观估算需求，给出一个区间，比如需求大约为d，d∈[d1,d2]，在这个区间中任意一个值均可能成为实际需求值，每个值成为实际值的可能性构成了各自的隶属度，隶属度函数就是来描述决策者对集合中各个数的信任程度的估计。

模糊方法可以用来对物流系统中不确定性需求进行描述，进而对不确定性需求下库存问题进行求解，构造模型以总成本最小原则求解相应的最佳订货点，指导库存策略的制定。

2 复杂物流库存模糊分析模型

库存系统考虑存量的变化情况，在有安全库存的情况下，存量若达到安全库存则报警，要求进行采购，复杂物流系统下，库存模型考虑一个订货周期内的订货量，即在库存报警至采购完成为一个周期最佳的订货量，对订货量考察多种控制策略与多个参与实体间的供需关系。以下首先明确一些要素的定义。

2.1 相关定义

供货比率：指供应方供应给需求方的货物量占该需求方需求总量的百分比。

缴纳周期：指需求方订货至收到货物的时间。

顾客需求：指零售商收到的终端顾客的订单需求。

实体特征：复杂物流系统的每一参与方的一些特征，包括单位保管成本与缺货成本。

保管成本：资金占用、仓库运营、设备折旧及其他费用，成本大小与库存量及保管产品的保管强度有关。

缺货成本：缺货是对于需求方而言的，但是一般供需双方会事先签订好协议，对供方不能及时供应需方产品而导致的损失将由供方赔偿，这就是缺货成本。

分散控制策略：所谓分散即物流系统中参与方的订货策略均从自身利益最大化角度出发。

部分调控策略：即存在核心企业，整个物流系统以核心企业的订货点为出发点来制定自身的订货点量。

物流链集成控制策略：该策略是供应链一体化的形式，整个系统内各参与方都视为同一家企业，订货策略从整体成本最优角度出发。

2.2 分散控制策略下最佳订货点模糊分析模型

其中

，，。

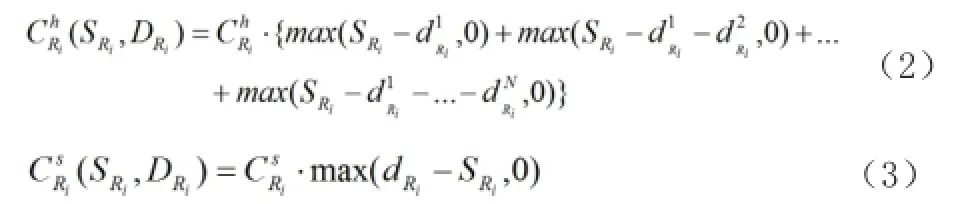
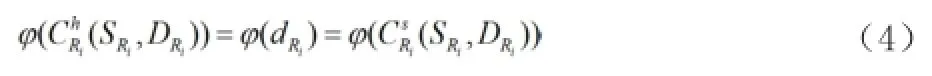
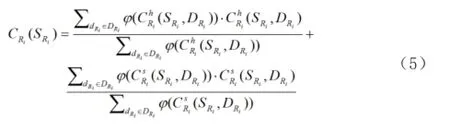
批发商的订货取决于零售商的需求，有上述零售商最佳订货点求解可知零售商一个周期内的模糊总需求为，隶属度为，对于批发商，若零售商单位时间段内订货需求为，，因为零售商作为批发商的客户不像消费者购买随机分布在时间段内，而是有规律的，在每个供货周期的第一个时间段内，需求量即为零售商的最佳订货点量，因此，假设批发商的保管成本与缺货成本分布为相对零售商的最佳订货点量为，则

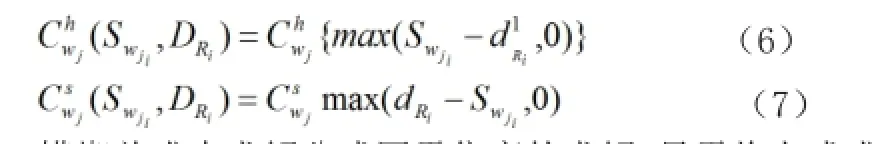
模糊总成本求解公式同零售商的求解，只需将上式成本计算代入即可，将不同的订货点量代入比较总成本大小则可以获得批发商相对零售商的最佳订货点量，对所有零售商，按照供货比率代入求解方程式求得相应的订货点量并加总，得到批发商的最佳订货点如下

对于制造商最佳订货点的求解可以运用批发商求解过程，将零售商视为制造商的间接顾客，只要将供货比率进行折算，令制造商对零售商的供货比率为，则

假设制造商的单位货物保管成本与单位客户需求缺货成本已知，则同理按照批发商的最佳订货点求解方法求得制造商的订货点量

（3）以零售商为核心控制策略下最佳订货点模糊分析模型

3 算例

假设复杂物流系统由零售商3个，批发商与制造商分别有2个构成，令单位时间与缴纳周期均为1周，盘点周期为3周，各商户的参数如表1所示，3个零售商的客户需求分别为9、14与20左右，模糊需求集表示如表2：

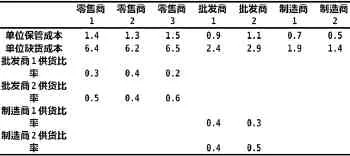
表1 各商户的参数表

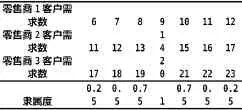
表2 需求模糊集表

运用构建的分散控制策略下模型对零售商的最佳订货点量进行求解，可以得到表3。

表3 两种方案最佳订货点

在分散控制策略下，以零售商1为例，依据公式（2）至公式（5）构建计算模型求解，对数据进行处理后可以求得当零售商订货点量为34件时，其总成本最小。当订货点量小于34时货物存量较少，保管成本低，但是缺货成本高昂，总成本随着订货点量的减少而增加；而订货点量超过34时，库存量的增长令货物保管成本直线增长，总成本居高不下，这符合实际库存规律。其中订货点量34是零售商采购的一个均衡点，可以作为零售商库存采购量的一个参考。同理根据式（8）与式（10）可以获得批发商1与制造商1的最佳订货点分别为64与72。可以看出订货点从下游至上游逐级递减，上游企业为应对采购需要更早地备货。分散控制策略下存在一定的问题，考虑的是销售终端的一个最为有利的情形，此种情形没有考虑批发商与制造商的利益，而是从单方面考虑，并且没有做好有效的供应链协调，没有考虑由此引起批发商与制造商库存成本上升而导致上游企业逆向选择，降低生产，进而影响零售商销售。

在以零售商为核心的控制策略下，上述的利益冲突的情形得到了统一，虽然还是考虑销售终端，但是终端销售与上游生产共享库存，供应链建立协调机制，批发商与制造商制定的库存策略更加准确，可以降低成本，零售商最佳订货点保持不变，以零售商1、批发商1与制造商1为例，根据式（11）及式（12）计算获得批发商1与制造商1的订货点为61与69，采购次数可以减少，库存可以保持在高位而无需承担过大的风险。

4 结语

本文通过算例证明了基于模糊需求物流库存建模求解问题的有效性，但是也存在不足之处，本文只对分散控制策略及以部分控制策略（以零售商为核心）下各实体最佳订货点进行了建模求解，而对于物流链集成控制策略下建模没有涉及，供应链集成将成为物流业发展的趋势，对于物流集成下库存系统模型分析有待进一步深入研究。

[1] 尹军琪.中国物流系统集成发展概述[J].物流技术, 2011,(18): 88-91.

[2] 郑圆圆,陈再良.模糊理论的应用与研究[J].苏州大学学报, 2011, 31(1): 52-58.

[3] 李永先,胡祥培,熊英.物流系统仿真研究综述[J].系统仿真学报,2017,19(7):1411-1416.

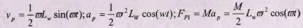
式中:Lw:表示活塞最大的行程

w：表示活塞运动的角频率

6 结语

综上所述，我们可见，SolidWorks的多功能自平衡护理的的设计，主要是从装配设计、运动仿真以及工作空间这几个方面进行了阐述，其研究后的自平衡护理床的功能主要是能够自动调平衡、床与轮椅之间能够互相转换以及床身起立，在医院、家用以及救护车方面得到了广泛应用，同时，促进了我国医疗事业的发展。

参考文献

[1] 李一民;;一种多功能气动抱夹装置的参数化设计及运动仿真研究[J];包装工程;2009年10期

[2] 张晓玲;张京伟;;医用护理床的设计[J];医疗卫生装备;2011年06期

[3] 辛绍杰;张欢欢;;护士机器人的系统设计及机构参数仿真优化[J];上海电机学院学报;2011年06期

[4] 张玉峰;张耀娟;;基于CAE技术的高度可调式医用转运车的设计[J];吉林化工学院学报;2011年11期

[5] 汪烨;;多功能电动护理床控制系统研制[J];制造业自动化;2009年06期

Inventory System Model Analysis of Complex Logistics based on Fuzzy Requirements

Wu Weide,Bai Tai,Luo Yinkang,Xiang Jingrui,Jin Xin
(Sichuan Province Electric Power Company measurement center,Sichuan Chengdu,610072)

Dynamics of the relationship of supply and demand in logistics system is similar to complex systems,for complex uncertain demand problem fuzzy set method is for solving in this paper.An inventory model is built based on fuzzy demand,upon decentralized control and distributed control strategy demand of retailers,wholesalers and suppliers are analyzed,and the model validity is verified by an example.

fuzzy requirements;complex logistics system;inventory system model