改进电路模拟法的应用——同构混合开关拓扑辨识
商慧亮, 刘 洋, 柳志栋, 董文杰, 李 锋
1.复旦大学电子工程系,上海200433
2.东方电子有限公司,山东烟台264000
长期以来,新型电力电子电路拓扑的建立主要依赖于灵感和经验,并没有一个严密的逻辑可以遵循.随着电路拓扑的日益复杂,有必要建立一种严密而有逻辑可循的电路拓扑建立方法.文献[1]对于在电路拓扑建立过程中如何确定有效的研究范围作了详细的介绍,其中一个重要的判定条件为结构条件,即根据图论等数学知识来剔除同构的电路拓扑,以生成一个最大不同构的电路拓扑基底.由此看来,在混合开关拓扑的建立过程中,需要解决一个很重要的问题——同构混合开关拓扑的辨识问题.
对混合开关拓扑进行数学建模,可以将同构混合开关拓扑的辨识问题转换为与其对应的含权无向图的同构判定问题.图的同构判定问题是图论研究中的一个基本问题,在电路拓扑[1]、机构学[2-3]、化学结构[4]、数据处理[5]等研究领域均有较为广泛的应用.对于图的同构判定问题,目前从理论上还无法证明它究竟属于NP完全问题还是P问题,于是众多学者予以关注和研究,并提出了各种图同构判定算法[6-15],主要包括改进的顶点顺序交换法、顶点度数序列法、基于神经网络的算法、基于搜索的算法等几类.其中基于搜索的算法在实际过程中表现最好,如SD算法、Ullmann算法、VF算法、Nauty算法等[12].文献[6-7]提出了一种新的图同构判定方法——电路模拟法,通过建模将图同构判定问题转换为判定其对应的伴随电路是否相同的问题,继而通过电路仿真来加以判定.理论分析和实际测试均表明,电路模拟法能够实现多项式时间复杂度内的随机图同构判定[7].
本文在原始电路模拟法的基础上进行改进,通过引入参考节点,进一步提高了电路模拟法的判定效率.在此基础上,结合对混合开关拓扑的数学建模,将改进的电路模拟法应用到同构混合开关拓扑的辨识中.经实例测试表明改进的电路模拟法在解决混合开关拓扑同构辨识问题上是有效的,且在判定速度以及节点匹配能力上有较大优势.
1 混合开关拓扑的定义和数学描述
1.1 混合开关拓扑的基本概念
开关拓扑是对含有电感、电容和开关元件的电力电子电路的抽象.考虑到效率因素,电阻元件在电力电子电路中通常作为负载出现在保护、采样电路中,因此在开关拓扑中一般不包含电阻元件.由电感、电容、开关元件、电压源、电流源组成的开关拓扑被称为混合开关拓扑[1].
1.2 混合开关拓扑的数学描述
文献[1]针对混合开关拓扑提出了一种较为直观的数学描述方法,该方法筛选出混合开关拓扑中所有有效的混合支路,并对其进行编号.参照这种方法,可以将混合开关拓扑中所有17种符合电路原理的有效的混合支路用图1所示的编号来表示.
1.2.1 混合开关拓扑的邻接矩阵表示
对于一个节点数为n的混合开关拓扑,设其任意两节点间最多存在1条图1所示的有效混合支路,那么其邻接矩阵D可定义为一个n×n的矩阵,其中第i行第j列元素

式中,e为混合开关拓扑中节点i和j之间所连接的混合支路在图1中所对应的编号.
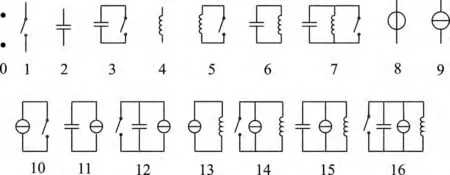
图1 有效的混合支路及其编号Figure 1 Valid hybrid branches and corresponding indices
例1给出了一个混合开关拓扑及其相应的邻接矩阵表示示例.
例1图2是一个典型的零电压转换PWM软开关升压斩波电路拓扑图,图中已对相关节点进行编号[1].

图2 混合开关拓扑示意图Figure 2 Example of hybrid switching topology
例如在图2中,节点2和5之间并联开关和电容,该混合支路在图1中对应的编号为3,所以在对应邻接矩阵中的第2行、第5列和第5行、第2列的元素值都是3.以此类推,可以列写出完整的邻接矩阵.
图2所示的混合开关拓扑所对应的邻接矩阵为

1.2.2 混合开关拓扑对应的含权无向图表示
对于一个给定的混合开关拓扑,以原先拓扑图中的节点为对应的含权无向图中的相应节点,以原先拓扑图中节点间连接的混合支路在图1中所对应的编号为含权无向图中相应节点间相连的边的权值,由此可以构建出混合开关拓扑所对应的含权无向图.若原先拓扑图中两节点间没有电路连接,则其对应的含权无向图中的相应节点间也没有边相连.
图3为图2所示的混合开关拓扑所对应的含权无向图.
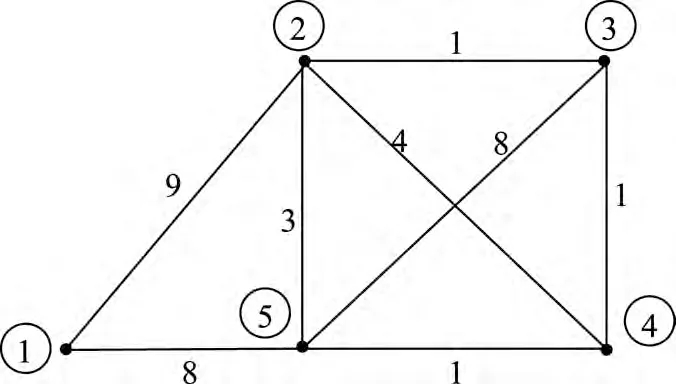
图3 混合开关拓扑对应的含权无向图的示意图Figure 3 Example of the corresponding undirectedweighted graph of hybrid switching topology
根据这种方法得到的含权无向图中的节点以及节点间的连接关系与原先混合开关拓扑中的节点以及节点间的电路连接是一一对应的.显然,若待判定的两个混合开关拓扑是同构的,则其分别对应的含权无向图也是同构的;反之亦然.于是,可以将同构混合开关拓扑的辨识问题转换为与其对应的含权无向图的同构判定问题.对此,本文在电路模拟法[6-7]的基础上进行改进,并提出了一种更高效的图同构判定算法——改进的电路模拟法.
2 改进的电路模拟法
2.1 电路模拟法的基本原理
基于文献[6-7],本节将针对含权无向图的同构判定简要地介绍电路模拟法的基本原理.
对于待判定图G和G′,若要满足同构,则图G和G′必须满足两个必要条件:1)顶点数相等;2)边数相等.如果不满足这两个条件,则可判定图G和G′不同构.
下面的叙述均假设图G和G′已经满足上述两个必要条件.本节将针对含权无向图引入度、相同电路、图的伴随电路、全激励、节点电压序列以及节点电压序列集等概念,并以此为基础推演出相关定理,从而奠定电路模拟法的理论基础.
定义1度图G中与一个点vi关联的边的数目被称为点vi的度[16].
定义2度数序列和度数分布序列对应统计G各顶点的度数,记下各顶点度数的数量统计,按照相同度数顶点的多少对度数进行排序.将相同度数少的顶点的度数排在前面,相同度数多的顶点的度数排在后面,度数相同的顶点的度数排在一起,从而得到度数序列.具有相同度数的各顶点的数量统计序列被称为度数分布序列.
例2图4为一对同构图G和G′.

图4同构图示例Figur e 4 Example of isomorphic graphs
图4 中(a)和(b)的各顶点度数分布统计如表1所示:
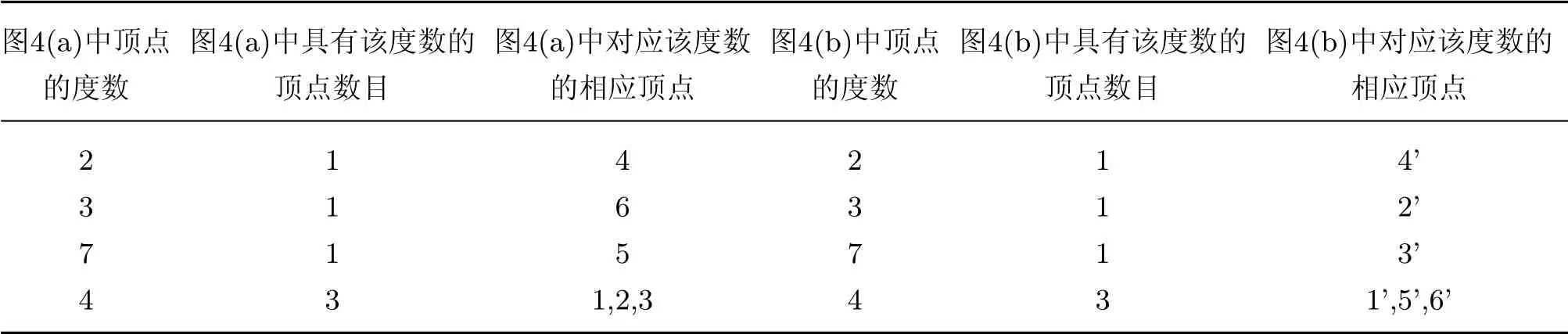
表1 图度数分布统计表Table 1 Degree distribution of vertices
那么图G和G′的度数序列和度数分布序列如下:
对于图G,度数序列为[2,3,7,4,4,4],度数分布序列为[1,1,1,3];
对于图G′,度数序列为[2,3,7,4,4,4],度数分布序列为[1,1,1,3].
定理1如果图G和G′是同构的,那么图G和G′对应的度数序列和度数分布序列是相同的.
定义3相同电路如果电路N和N′对应的拓扑图G和G′是同构的,并且对应支路上具有相同的元件,那么电路N和N′称为相同电路,记为N=N′.
定义4图的伴随电路对于含权无向图G,将图中每条边均用电阻替代,让电阻的导纳值等于图G中相应边的权值,由此得到的电路N被称为图G的伴随电路.
例3如图5所示,将图(a)所示的含权无向图G中的每条边均用电阻替代,使电阻的导纳值等于图G中相应边的权值,由此可以得到图(b)所示的伴随电路N.

图5 图的伴随电路示意图Figure 5 Example of a graph and its corresponding associate circuit
定理2同构图所对应的伴随电路是相同电路;反之,互为相同电路的伴随电路所对应的图是同构的.
定义5全激励在含有n个节点的伴随电路N中,若以节点i为参考点,在节点i与其余(n-1)个节点间分别施加相同的电流源Is(为便于计算,相同的电流源Is选用1A),电流方向都是从节点i指向其余节点,这样一种激励方式称为节点i的全激励.图5(b)所示的伴随电路N中以节点1为参考点施加全激励的情况如图6所示.
定义6节点电压序列和节点电压序列集在包含n个节点的伴随电路N中,以节点i为参考点施加全激励,将得到的节点电压序列按照升序排列(相等的电压排列在一起),得到的电压序列Si(i=1,2,3,···,n)称为节点i的节点电压序列.对伴随电路N中所有节点依次施加全激励,得到的所有节点电压序列的集合称为节点电压序列集,记为SN={Si},i=1,2,···,n.
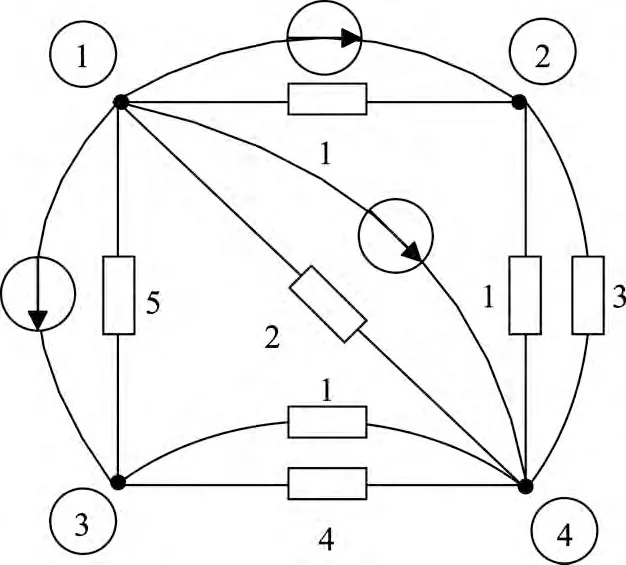
图6 节点1的全激励示意图Figur e 6 Complete excitation of node 1
定理3对图G和G′所对应的伴随电路N和N′中所有节点施加相同全激励,若图G和G′同构,那么所得到的节点电压序列集是相同的,并且N和N′中对应节点的节点电压序列相等.
定理4设图G和G′对应的邻接矩阵分别为D和D′,对应的伴随电路分别为N和N′,对伴随电路N和N′中所有节点施加相同全激励.如果得到的节点电压序列集SN=SN′,并且SN和SN′中的节点电压序列各不相等,根据SN和SN′中节点电压序列间的对应关系调整图G′对应的邻接矩阵D′,调整规则如下:
对于有n个节点的图G和G′,若图G中节点i所对应的节点电压序列Si与图G′中节点j′所对应的节点电压序列Sj′相等,那么图G中的节点i与图G′中的节点j′互为对应节点,记j′为π(i).而定理4中已假设节点电压序列集SN=SN′,并且SN和SN′中的节点电压序列各不相等,因而可以得出所有节点间的对应关系:i↔π(i)(i=1,2,3,···,n),其中i为图G中的节点,π(i)为图G′中与节点i成对应关系的节点的编号.
在此基础上,根据节点间的对应关系调整图G′对应的邻接矩阵D′.首先依次将D′中的第π(i)行存放于一个中间矩阵Dn的第i行(i=1,2,3,···,n),然后将Dn中的第π(i)列依次存放于最终调整后得到的矩阵的第i列(i=1,2,3,···,n).
在此基础上可以得到如下结论:
定理5图G和G′对应的伴随电路分别为N和N′,对伴随电路N和N′中所有节点施加相同全激励,假设得到的节点电压序列集SN=SN′,如果图G和G′同构,那么仅节点电压序列相等的节点所对应的图的顶点间可能存在对应关系.
定理1~5的详细证明见文献[6-7],这里不再赘述.
2.2 电路模拟法的改进
在同构判定过程中若采用原始的电路模拟法,则待判定图所对应的伴随电路中的所有节点应轮流作为施加全激励的参考点,从而得到作为同构判定依据的节点电压序列.因此,对于顶点数为n的两个图,一次完整的同构判定过程需要遍历所有2n个顶点,并依次施加全激励以求解节点电压序列.理论分析和实验结果均表明,原始的电路模拟法能够实现多项式时间复杂度内的随机图同构判定[6].为进一步提高电路模拟法的判定效率,本文提出了一种增加参考顶点的改进措施,通过对待判定图进行预处理,使得在判定顶点数为n的两个图时,只需计算对新增的参考顶点施加全激励得到的节点电压序列,于是大大降低了算法的计算复杂度.
2.2.1 待判定图的预处理
本节将针对含权无向图介绍改进的电路模拟法对待判定图的预处理过程.
预处理规则如下:对于有n个顶点的待判定图G,增加一个参考顶点,记为顶点m,将顶点m与其余n个顶点分别用含权无向边ki(i=1,2,···,n)相连,其中ki表示顶点m与顶点i之间相连的含权无向边,边的权值等于顶点i的度数.
例4 对于图5(a)所示的含权无向图G,根据待判定图预处理规则进行预处理,得到的图Gm如图7所示.
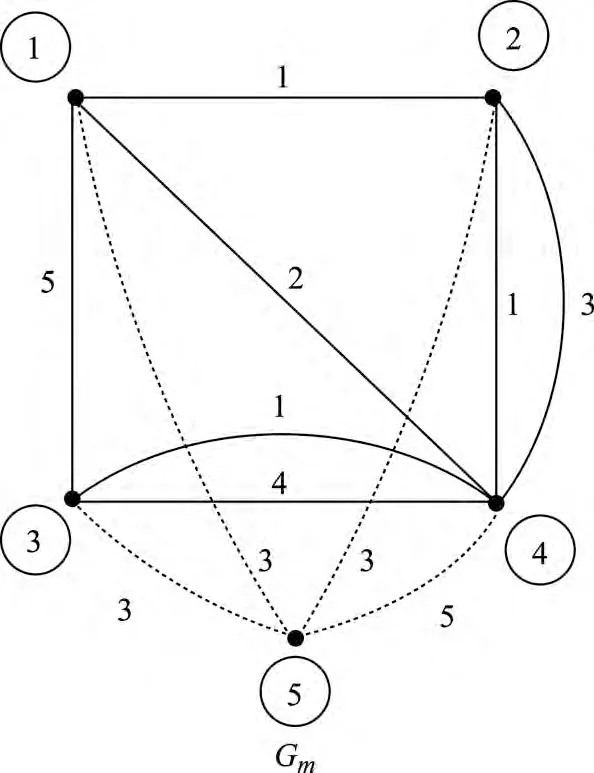
图7 待判定图预处理示例Figure 7 Example of the pre-processing of the graph to be determined
定理6如果待判定图G和G′是同构的,那么图G和G′分别根据预处理规则处理后得到的图Gm和也是同构的,且新增的参考顶点互为对应顶点.
由预处理规则可知:对于有n个顶点的图G和G′,如果它们是同构的,那么经过预处理后得到的图Gm和中增加的参考顶点m和m′与原图中对应顶点间的连接均是相同的,不影响原图中顶点间的对应关系,因此预处理后的图Gm和也是同构的,且顶点m和顶点m′互为对应顶点.
在定理6的基础上,根据定理3可以得出:对图Gm和对应的伴随电路Nm和中的节点m和m′分别施加相同全激励,得到的节点电压序列Sm和相等.
类似于定理4,可以推导出定理7.
定理7 设顶点数为n的图G和G′对应的邻接矩阵分别为D和D′,根据预处理规则分别对图G和G′进行预处理得到图Gm和,构建相应的伴随电路Nm和,分别以新增的顶点m和m′作为参考节点施加相同全激励,如果得到的节点电压序列Sm=,且Sm和中各个节点电压各不相等,那么根据Sm和中节点电压间的对应关系调整图G′对应的邻接矩阵D′(具体的操作参照定理4中的调整规则),调整后的矩阵为,在此基础上可得到如下结论:
1)若D′n=D,则可判定图G和G′同构.
2)若D′n/=D,则可判定图G和G′不同构.
类似于定理5,可以推导出定理8.
定理8 根据待判定图预处理规则对待判定图G和G′进行预处理,分别增加参考顶点m和m′,得到图Gm和,构造相应的伴随电路Nm与,并以节点m和m′为参考点施加相同全激励.假设得到的节点电压序列Sm=,那么图G和G′同构,仅节点电压相等的节点所对应的图的顶点间可能存在对应关系.
对于预处理后得到的图Gm和所对应的伴随电路Nm和来说,新增的参考顶点m和m′是唯一的度数最大的点,因此可以唯一确定,这样只需对新增的参考节点施加全激励,然后比较得到的节点电压序列即可判定两图是否同构.由于原始的电路模拟法需遍历待判定图所对应的伴随电路中所有的节点并施加全激励,改进的电路模拟法的判定效率大大提高了.
2.2.2 改进的电路模拟法的判定流程
本节将给出改进的电路模拟法的判定过程.
假设待判定图G和G′满足图同构的两个必要条件:1)顶点数相同;2)边数相等.如果不满足上述任何一个条件,则可直接判定图G和G′不同构;如果满足,则继续下面的步骤1~7:
步骤1写出图G和G′对应的邻接矩阵D和D′.
步骤2对图G和G′中顶点的度数分布进行统计,如果统计得出的度数序列和度数分布序列均相等,则继续步骤3~7,否则可判定图G和G′不同构,判定过程终止.
步骤3根据预处理规则对图G和G′进行预处理,得到图Gm和.
步骤4构建图Gm和对应的伴随电路Nm和,并以新增的节点m和m′作为参考节点施加相同全激励,构建节点电压方程,求出相应的节点电压序列Sm和S′m.
步骤5比较节点电压序列Sm和,若不相等则可判定图G和G′不同构,判定过程终止;若Sm=则两图可能同构,检测Sm和中有没有相同的节点电压,如果有,跳至步骤7,否则继续.
步骤6根据节点电压序列Sm和中得出的顶点间的对应关系调整G′的邻接矩阵D′,若调整后得到的矩阵=D,则可判定图G和G′同构,否则两图不同构,判定过程终止.
步骤7Sm和中含有相同的节点电压,表明待判定图中存在对称顶点.对具有相同节点电压的顶点列出其所有可能的对应关系,根据每一种对应关系相应调整G′的邻接矩阵D′.若调整后得到的矩阵=D,则可判定图G和G′同构;若经过所有可能的调整后/=D,则可判定图G和G′不同构.
3 同构混合开关拓扑辨识实例
本文第1节介绍了如何通过建模将同构混合开关拓扑的辨识问题转换为其相应的含权无向图的同构判定问题,在此基础上,本节将改进的电路模拟法和特征值判定法应用到同构混合开关拓扑辨识上,并分别给出判定实例.
以图2所示的电路拓扑为基础,图8给出了该电路的一对同构混合开关拓扑,且已对电路中的节点进行编号.
本节将分别应用文献[1]提出的特征值判定法以及本文提出的改进的电路模拟法分别对图8所示的一对混合开关拓扑进行同构判定.
3.1 特征值判定法
对于混合开关拓扑的同构判定,文献[1]提出了一种有效的判定方法——特征值判定法,其基本流程如下:先根据混合开关拓扑的数学表示方法列出其邻接矩阵,再判断计算出的邻接矩阵的特征值是否相等.若不相等,则不同构;若相等,则两个开关拓扑所对应的邻接矩阵相似.计算这两个相似矩阵之间的相似变换矩阵,如果其相似变换矩阵为置换矩阵,则两个开关拓扑是同构的,否则不同构.
根据本文第1节提出的混合开关拓扑的数学描述方法可以将图8所示的两个混合矩阵拓扑的邻接矩阵D和D′分别表示为

图8 同构混合开关拓扑示意图Figure 8 Example of isomorphic hybrid switching topology

根据特征值判定法,使用Visual C++进行编程,编程环境为:Windows7,Pentium Dual-core CPU T4200 2.0GHz×2,2GB RAM.输入待判定的混合开关拓扑的邻接矩阵D和D′,其计算结果如下:
首先算出邻接矩阵D的特征值

邻接矩阵D′的特征值为

比较可得两组特征值相等,表明输入的两个邻接矩阵相似.接着计算邻接矩阵间的相似变换矩阵,其相似变换矩阵T为
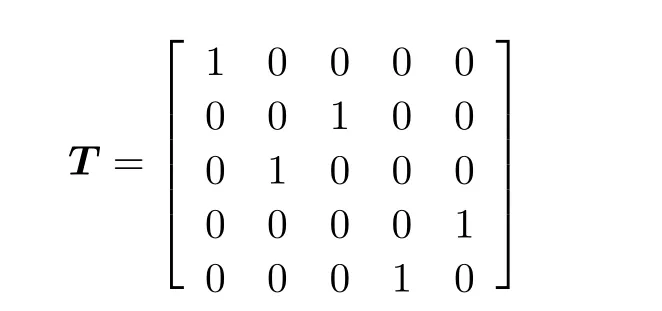
满足D′=T-1D T
显然相似变换矩阵T为置换矩阵,于是可以判定两开关拓扑同构,但在这种情况下并不能直接得到同构的混合开关拓扑中节点的对应关系.
3.2 改进的电路模拟法
首先构建图8所示的一对混合开关拓扑所对应的含权无向图G和G′,如图9所示:
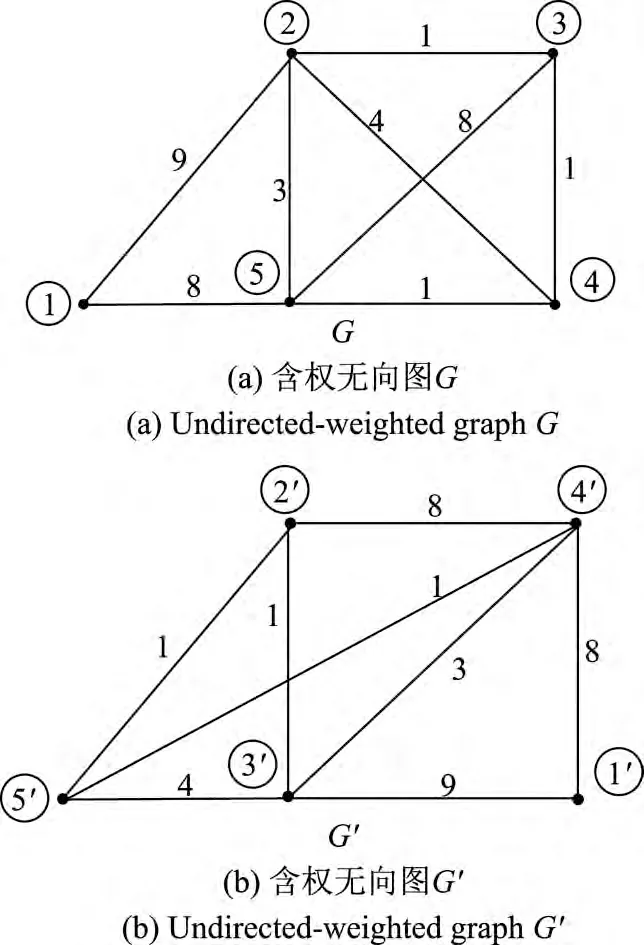
图9 混合开关拓扑对应的含权无向图Figure 9 Hybrid switching topology and corresponding undirected-weighted graph
对图9所示的含权无向图G和G′中的顶点度数分布进行统计,得到的统计结果见表2.
那么图G和G′的度数序列和度数分布序列分别如下:
对于图G,度数序列为[2,3,3,4,4],度数分布序列为[1,2,2];对于图G′,度数序列为[2,3,3,4,4],度数分布序列为[1,2,2].
根据改进的电路模拟法中提出的待判定图的预处理规则,可以得到图9所示的含权无向图G和G′经过预处理后得到的图Gm和G′m,如图10所示.

图10 预处理后的含权无向图Figure 10 Pre-processed undirected-weighted graph
相比于图9所示的原始的含权无向图G和G′,图10所示的Gm和分别增加了顶点6和6′作为参考顶点,并将参考顶点和原图所有的顶点都用含权无向边连接起来(其权值为原图对应顶点的度数).

表2 度数分布统计表Table 2 Degree distribution of vertices
构造图Gm和对应的伴随电路Nm与,如图11所示.

图11 预处理后的含权无向图对应的伴随电路Figure 11 Corresponding associated circuits of thepreprocessed undirected-weighted graphs
分别以节点6和6′作为参考点施加全激励,将所有的电流Is设为1A,列写节点电压方程.
对于无向含权图Gm对应的伴随电路Nm,节点电压方程为


解得的节点电压分别为

节点6和6′对应的节点电压序列S6和S6′分别为
S6=[0.3069,0.3069,0.3137,0.3165,0.3272],
可以发现节点电压序列S6和中的节点电压一一对应相等,且每个序列中的电压值各不相等.由此可以判定原先的混合开关拓扑可能是同构的,根据节点电压间的对应关系,可以得出其顶点间可能的对应关系为1-1′,2-3′,3-2′,4-5′,5-4′.
根据对应关系交换G′对应的邻接矩阵D′,得到矩阵

在此基础上,本文针对更大规模的混合开关拓扑分别采用改进的电路模拟法和特征值判定法进行同构判定测试,在Windows7,Pentium Dual-core CPU T4200 2.0GHz×2,2 GB RAM的配置环境下,比较两种判定方法同构判定所消耗的时间,判定0~150个点的拓扑的平均耗时如图12所示.
由图12可以发现,改进的电路模拟法的判定耗时远小于特征值法,在处理150个点以内的混合开关拓扑的同构判定时,改进的电路模拟法的耗时变化不大,最大耗时在0.016s.而特征值判定法的耗时则随着电路节点数的增加而急剧增加,判定150个节点的电路拓扑的耗时为6.2240s,远大于改进的电路模拟法.由此可见,改进的电路模拟法在判定速度上有较大的优势.
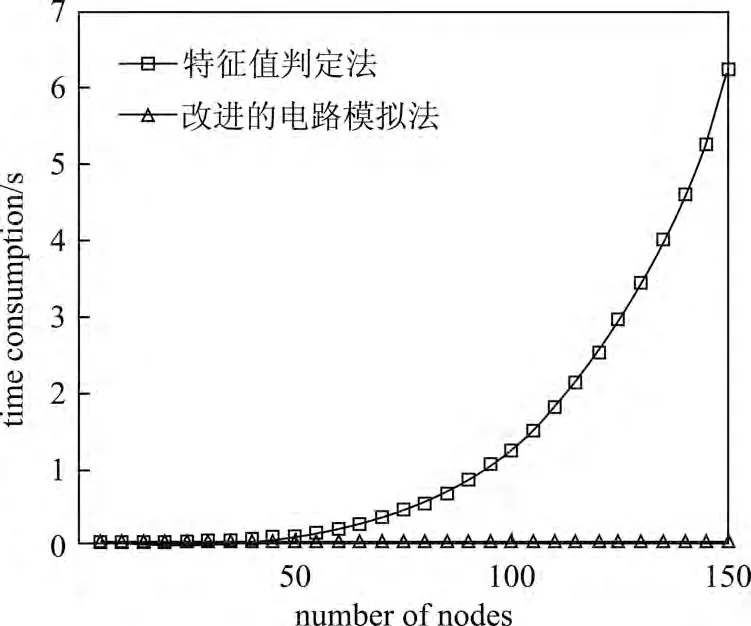
图12 改进的电路模拟法和特征值判定法的耗时比较Figure 12 Comparison of time consumtions between optimized circuit simulation method and eigenvalue algorithm
3.3 改进的电路模拟法与特征值判定法的比较分析
3.3.1 节点匹配能力
特征值判定法先通过计算来比较两个电路邻接矩阵的特征值,并判定两个拓扑所对应的邻接矩阵是否相似,接着判定邻接矩阵间的相似变换矩阵是否为置换矩阵,进而判定混合开关拓扑是否同构.假设判定得出两个拓扑同构,则该方法只能得到两个电路拓扑的邻接矩阵之间的相似变换矩阵,而不能直接得到原先电路拓扑中节点间的对应关系.
改进的电路模拟法首先将混合开关拓扑的同构判定问题转换为对应的含权无向图的同构判定问题,接着构建含权无向图的伴随电路进行电路仿真,解得节点所对应的节点电压,最后判断解得的节点电压值是否完全对应相等来判定混合开关拓扑是否同构.由于解得的节点电压值和电路拓扑中的节点是一一对应的,节点电压对应相等的两个节点分别对应的电路拓扑中的节点也互为对应关系,于是可以直接得出同构的电路拓扑中节点间的对应关系.
3.3.2 算法复杂度分析
假设待判定的混合开关拓扑有n个节点,那么采用改进的电路模拟法进行同构判定时在最优情况下的计算复杂度主要依赖于以下几个步骤:
步骤1列写节点电压方程的通用导纳矩阵,运算次数为2次,单次运算的时间复杂度为O((n+1)2).
步骤2求解节点电压方程,方程维数为n,运算次数为2次,由于图的伴随电路节点电压方程一般为稀疏矩阵线性方程组,因而本算法采用广义最小残差法[17]来解,单次运算的时间复杂度为O(n2).
步骤3根据计算得到的一对节点电压序列获得节点间的对应关系,其运算次数为1次,单次运算的时间复杂度为O(n2).
步骤4根据节点间的对应关系调整其中一个邻接矩阵,其运算次数为1次,单次运算的时间复杂度为O(n2).
步骤5将调整后的邻接矩阵与未调整的邻接矩阵作比较运算,运算次数为1次,单次运算的时间复杂度为O(n2).
由此可见,对于改进的电路模拟法,在最优情况下的算法时间复杂度在O(n2)量级上.对于一些对称性较强的图,节点电压序列中可能出现节点电压相同的情况,此时需要遍历这些节点间所有可能的对应关系,相应地调整邻接矩阵,得出最终的判定结果.在这种情况下,改进的电路模拟法的判定效率会有所降低,但不影响算法的正确性,且这种情况在实际电路拓扑中并不多见.
对于特征值判定法,应先求解邻接矩阵的特征值,再计算相似变换矩阵,因此算法的计算大多集中在电路拓扑邻接矩阵的特征值和特征向量上.随着电路节点数目的增加,混合开关拓扑的邻接矩阵一般为稀疏矩阵,因而特征值判定法在实现过程中采用Jacobi迭代法来求解邻接矩阵的特征值和特征向量.对于一个n阶的混合开关拓扑,该方法的时间复杂度为O(n3),而其余计算步骤的复杂度均在O(n2)量级上,因而特征值判定法总体的算法时间复杂度在O(n3)量级上.随着待判定开关拓扑节点数的增加,改进的电路模拟法与特征值判定法的算法耗时差距急剧加大,这也与图12所示的测试结果相符合.
由此可见,改进的电路模拟法在节点匹配能力以及算法时间复杂度上较特征值判定法有较大的优势.
4 结语
本文基于图同构判定算法——电路模拟法[6-7],通过对待判定图增加一个参考顶点的改进,大大提升了原先算法的判定效率.在此基础上,参照文献[1]中对混合开关拓扑的数学描述,将改进后的电路模拟法巧妙地运用到混合开关拓扑的同构判定中,并由理论分析和实例证明了该方法的有效性,同时将改进的电路模拟法与特征值判定法进行比较,证明了改进的电路模拟法在判定速度和节点匹配能力方面的优势.
[1]石勇,杨旭,何群,王兆安.同构混合开关拓扑的辨识[J].中国电机工程学报,2003,23(11):116-121.SHIYong,YANGXu,HEQun,WANGZhao'an.Identif ication of hybrid switching topology[J].Proceedings of the Chinese Society for Electrical Engineering,2003,23(11):116-121.(in Chinese)
[2]丁华锋,黄真.平面机构统一拓扑描述模型的建立及同构判别[J].机械工程学报,2009,45(3):99-103.
DING Huafeng,HUANG Zhen.Uniform topological representation model of planar mechanisms and isomorphism identif ication[J].Journal of Mechanical Engineering,2009,45(3):99-103.(in Chinese)
[3]丁玲,路懿.运动链拓扑图的特征数组表示及同构判断[J].机械工程学报,2010,46(7):63-67.
DING Ling,LU Yi.Character arrays representation and isomorphism identif ication of kinematic chain topology graphs[J].Journal of Mechanical Engineering,2010,46(7):63-67.(in Chinese)
[4]GOLOVAN A,HENRICK K.Chemical substructure search in SQL[J].Journal of Chemical Information and Modeling,2009,49(1):22-27.
[5]CHEN Kai,GUO Chuanxiong,WU Haitao,YUAN Jing,FENG Zhenqian,CHEN Yan,LU Songwu,WU Wenfei.Generic and automatic address conf iguration for data center networks[C]//Proceedings of the ACM SIGCOMM 2010 Conference.New Delhi,India,2010:39-50.
[6]SHANGH,LIF,TANGX,WOOP Y.A new algorithm for isomorphism determination of undirected graphscircuit simulation method[J].Circuits,Systems,and Signal Processing,2011,30(5):1115-1130.
[7]LIF,SHANGH,WOOP Y.Determination of isomorphism and its applications for arbitrary graphs based on circuit simulation[J].Circuits,Systems,and Signal Processing,2008,27(5):749-761.
[8]SHANG Huiliang,LI Jichuan,CAI Qi,DONG Wenjie.An optimized algorithm for the identif ication of isomorphic undirected graphs[C]//Proceedings of 2011 International Conference on Modelling,Identif ication and Control,ICMIC 2011,Shanghai,2011:351-356.
[9]李锋,李晓艳.图的同构判定算法:关联度序列法及其应用[J].复旦学报:自然科学版,2001,40(3):318-325.
LIFeng,LI Xiaoyan.Isomorphism testing algorithm for graphs:incidence degree sequence method and applications[J].Journal of Fudan University:Science Edition,2001,40(3):318-325.(in Chinese)
[10]李锋,商慧亮.有向图的同构判定算法:出入度序列法[J].应用科学学报,2002,20(3):258-262.
LI Feng,SHANG Huiliang.An isomorphism testing algorithm for directed graphs:the in-degree and outdegree sequence method[J].Journal of Applied Science,2002,20(3):258-262.(in Chinese)
[11]南晋华,齐欢.图同构问题的决策神经网络模型[J].计算机学报,2010,33(2):300-304.
NAN Jinhua,QI Huan.The decision-making neural networks model for solving the graph isomorphism problem[J].Chinese Journal of Computers,2010,33(2):300-304.(in Chinese)
[12]PORUMBEL D C. Isomorphism testing via polynomial-time graph extensions[J].Journal of Mathematical Modeling and Algorithms, 2010,10(2):119-143.
[13]ZAHIDI U A.Spectral solution for detecting isomorphic graphs with nondegenerate eigenvalues[C]//11th IEEE International Multitopic Conference,INMIC2007.Lahore,Pakistan,2007:1-4.
[14]QIU Ming,HU Haibin,JIANG Qingshan,HU Hailong.A new approach of graph isomorphism detection based on decision tree[C]//2nd International Workshop on Education Technology and Computer Science,ETCS 2010,Wuhan,Hubei,2010:32-35.
[15]ZHANG Baida,TANG Yuhua,WU Junjie,HUANG Linqi.A unique vertex deleting algorithm for graph isomorphism[C]//2011 International Symposium on Image and Data Fusion,2011,Tengchong,Yunnan,2011:1-4.
[16]徐俊明.图论及其应用[M].安徽:中国科学技术大学出版社,1998:16.
[17]MEISTER A. Numerik linearer gleichungssysteme[M].2nd ed.Germany:Vieweg,2005.

