无人机俯仰角增益调参控制律设计

（张家界航空工业职业技术学院航空维修工程系，湖南张家界，427000）

无人机俯仰角增益调参控制律设计

王 波

（张家界航空工业职业技术学院航空维修工程系，湖南张家界，427000）

针对传统增益调参控制系统设计过程中离线工作量大的问题，研究设计了无人机俯仰角增益调参控制系统。首先对无人机模型进行线性化和简化处理，得到俯仰角系统模型；其次针对不同特征点处的子模型，利用根轨迹法设计得到阻尼器，利用Ziegler-Nichols以及Signal Constraint方法整定得到PID参数，得到增益调度表；然后利用sftool工具箱生成全局控制器；最后对得到的无人机俯仰角控制系统进行仿真。仿真结果表明，所设计的无人机俯仰角控制系统在全局范围内具有良好的动态响应性能。

增益调参；无人机；根轨迹;Ziegler-Nichols；Signal Constraint.

0 引言

随无人机飞行包线的扩大，无人机运动的数学模型也随飞行状态产生摄动，这时一套参数就难以兼顾较大包线范围内的飞行品质。针对此问题国内外现代控制理论方法基本处于仿真层面，应用于工程实际任需克服重重障碍。PID增益调参法作为无人机飞控系统的主要手段，也存在离线计算量大、控制系统性能有限等问题。本文利用根轨迹法设计阻尼器，利用Ziegler-Nichols及Signal Constrant方法整定PID参数，利用sftool生成全局控制器，方法简单，计算量小，且使无人机俯仰角控制系统达到了一级飞行品质标准。

1 增益调参

增益调参(gain-schedule)的思想是：根据不同的平衡工作点分别设计局部控制器，形成覆盖控制对象整个动态特性范围的增益调度表，并利用某种类型的插值或拟合得到控制器增益与调度变量在各个平衡工作点以及平衡工作点之间的调参规律曲线(曲面)，实现控制对象的控制。

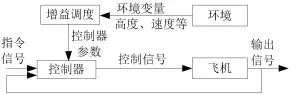
图1 程序调参控制律原理图

增益调参飞行控制律实质上是增益调度控制。根据动压、静压等，按预定程序实时调节控制器参数，以适应数学模型的变化，原理如图1。

2 无人机纵向短周期运动

无人机是一个多输入多输出的非线性系统，假设飞机水平无侧滑飞行，经线性化处理，可得小扰动线性化状态方程。在小扰动条件下，无人机的纵向和横侧向运动耦合不严重，因此把运动方程分解为相互独立的纵向和横侧向运动分别研究。飞机的纵向运动又可分为两个阶段：初始阶段是以迎角和俯仰角速率变化为代表的短周期运动,飞行速度基本不变；之后的阶段是以飞行速度和航迹倾斜角的变化为代表的长周期运动,飞机迎角基本不变。

利用短周期运动的固有频率和阻尼比关系，可以得到俯仰角速率的传递函数为：

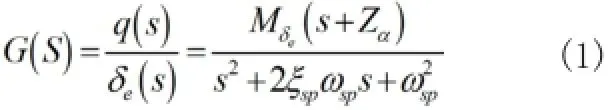
3 俯仰角控制系统设计

俯仰角速率反馈的俯仰角控制系统原理如图2，虚线框内为阻尼回路，故称K为阻尼器。按经典设计分别设计阻尼器K和PID控制器。

图2 具有俯仰角速率反馈的俯仰角控制系统

3.1选取平衡点

在全局飞行包线内选取21个典型特征点，建立其线性时不变模型，根据Mach number图选取特征点。高度和马赫数的范围为：

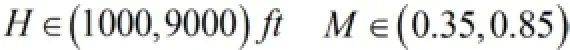
3.2阻尼器设计

俯仰阻尼器主要是用来改善飞机的纵向短周期运动的阻尼特性。某些标准上，无人机可参照有人机的指标要求。GJB185-86规定，一级飞行品质标准要求在0.35～1.30之间。选择合适K，系统的短周期阻尼就可得到改善。

取任意特征点，例(M,H)=(0.6,1000)，可算出升降舵到俯仰角速率q(t)的传递函数为：

图2中舵机模型采用一阶惯性环节，可得，内回路系统的开环传递函数为

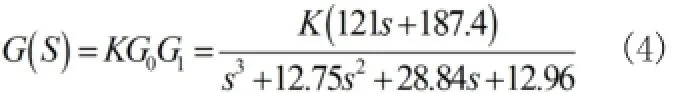
由此可画出阻尼回路随增益K变化的根轨迹，由图可知，当阻尼器K=0.425时，短周期阻尼比ξsp=0.707，满足一级飞行品质标准要求。

3.3PID控制器设计

外回路控制设计目的是使俯仰角能快速跟踪参考输入，并尽量消除静态误差。本节利用连续ZN方法及基于SC优化的PID参数整定设计PID控制器，达到系统满意的要求。

ZN整定公式如下：

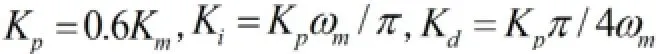
Km为系统开始震荡的增益值，为震荡频率。

在PID控制器未整定时，可在外回路控制系统的开环根轨迹图上得到穿越轴时的增益值为Km=5.91，频率为=7.97rad/ s。利用ZN整定公式可以求的PID控制器参数为：

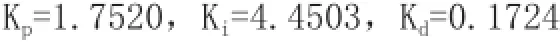
PID整定后的闭环根轨迹如图3，由图可见，极点均位于负半平面，达到完全稳定状态。

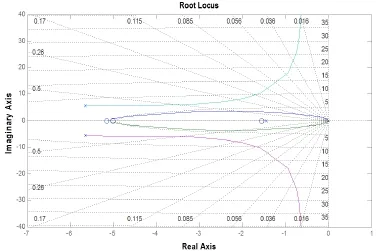
图3 外回路控制系统的开环根轨迹

俯仰角的阶跃响应曲线如图4。

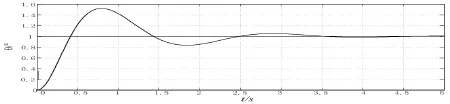
图4 俯仰角阶跃响应

分析图4可知，俯仰角响应能较快速跟踪俯仰角指令信号，调节时间为3.2s，没有稳态误差，但是超调量为50%，所以ZN整定的PID控制器并不完全满足控制要求，PID参数需进一步整定。

利用simulink design optimization工具箱中的特定模块对系统进行自动优化实现。

优化的关键在于PID控制器参数初值的设定，初值设定不当很可能造成SC无法运行。所以，这里采用ZN方法整定得到的PID参数作为初值，最后优化得到PID参数为：

Kp=1.7530，Ki=0，Kd=0.1747

4 全局增益调参控制器

4.1增益调度表

按上节描述的俯仰角控制系统设计方法，可求得全局飞行包线内其他所有特征点处的阻尼器K和外回路PID控制器的参数，从而得到增益调参的增益调度表，如表1（部分）。

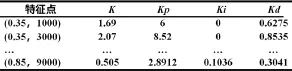
表1 增益调度表

4.2生成增益调参控制器

利用sftool工具箱，将获得的特征点处的控制器参数进行直接拟合，得到控制器参数关于高度(H)和马赫数(M)的函数，如此，得到全局内控制器参数随参变量连续变化的规律。

用拟合而成的控制器去控制飞行包线内的任意点，若仿真结果无法达到或不能完全达到性能指标要求，第一种可能是拟合精度低，需要增加特征点个数；第二种可能是拟合产生的控制器，本身无法保证全局的稳定性，需要采用其他方法进行分析。若仿真结果能达到性能指标要求，则说明拟合获得的控制器是有效的。

5 仿真验证

为验证所设计控制系统性能，在飞行包线内取特征点外的任意点仿真。

假设无人机运动到飞行包线内的某一点，如点(M,H)=(0.55,5000)。此时，由式(5)可以求得阻尼器和PID控制器参数为：

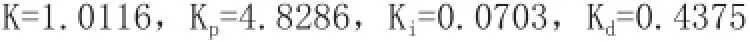
由图5可以看出，俯仰角的响应值能够快速跟踪参考信号，调节时间仅为1.59s，超调为5%，无稳态误差。俯仰角速率的最大增量为2.83/s，舵偏角最大偏量为4.83。由此可以看出，拟合得到的控制器能够很好的保证工作点处的系统性能。

为进一步验证全局控制器能，下面对除特征点外的16个点进行验证。所得16个点处的控制器参数和系统性能指标(部分)如表2所示。

从表2各点的时域性能指标可见，拟合全局控制器能使各工作点的控制系统达到满意的性能，故拟合得到的全局控制器是有效的。

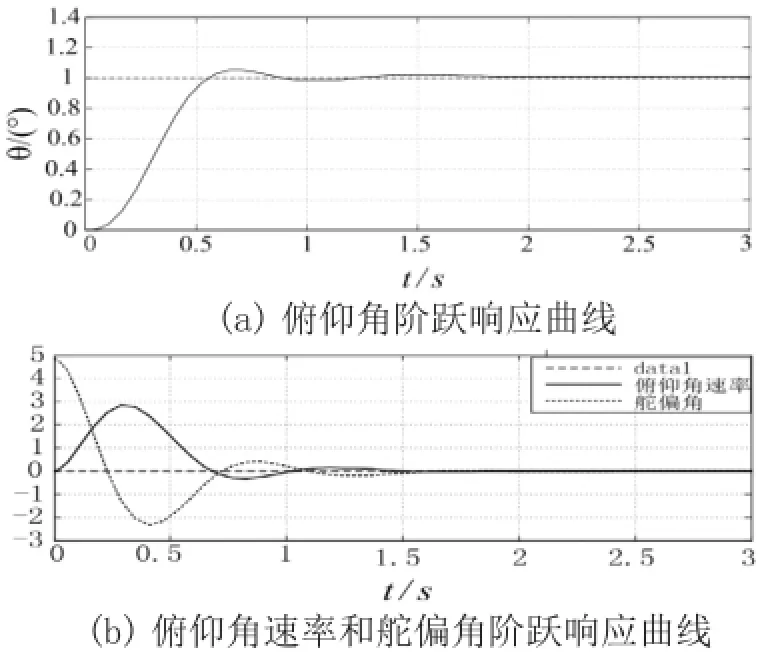
图5 俯仰姿态保持的阶跃响应仿真曲线

表2 工作点的控制器参数和性能指标

6 总结

本文立足工程应用，以减少传统增益调参控制系统设计工作量为目的，对某型无人机俯仰角增益调参控制系统进行了设计和仿真验证。设计的主要特点在于局部PID控制器参数的整定以及全局控制器的生成，方法简单有效，降低了离线设计工作量，具有工程应用价值。

[1] 李中健,安锦文.全包线飞行控制系统设计方法研究[J].飞行力学, 2001,19(1):529.

[2] 郭锁凤,申功璋等.先进飞行控制系统[M].北京:国防工业出版社,2003

[3] 武晓光,刘林.基于线性参变模型的大包线飞行控制系统设计[J].弹箭与制导学报,2006,26(1):353.

[4] 刘金琨.先进PID控制MATLAB仿真[M].电子工业出版社,2011.3.

The Gain Schedule Control Law’s Design of a UAV’s Pitching Angle

Wang Bo
(College of Aviation Maintenance and Engineering,ZhangJiajie Aviation Industry Vocational College, ZhangJiajie，427000,China)

Aiming to the problem that the design process of traditional gain-scheduling control system is a big workload,the pitching angle control system was designed based on the thought of gain-scheduling. Firstly,the UAV’s model was linearized and simplified;secondly,the UAV’s pitching angle dampers in each equilibrium point were designed using root locus method,meanwhile,the PID controllers were designed by using Ziegler-Nichols and Signal Constraint,then the gain-scheduling table was got;third,the global controller was realized by sftool;at the last,simulation results show the gain-scheduling control system was effect,and the fight control system has good dynamic performance in the whole envelope.

gain-schedule;UAV;root locus;Ziegler-Nichols;Signal Constraint.

TP273；V294.1

A

王波（1987-），女（土家族），湖南张家界人，硕士，助教，主要研究领域为先进控制理论及其应用。