基于BP神经网络和iSIGHT平台的风电机组设计年发电量预测
文 | 周书锋 方郁锋
基于BP神经网络和iSIGHT平台的风电机组设计年发电量预测
文 | 周书锋 方郁锋
随着中国风电产业多年的快速发展,风电技术人员已经积累了大量的设计、测试和运行数据。在大数据时代背景下,如何对这些数据进行分析和挖掘,总结内在规律,开发外延应用,对今后的风电技术发展有着重要意义。
人工神经网络简称神经网络,是一种非线性统计性数据建模工具,常用来对输入和输出间复杂的关系进行建模。神经网络可以通过有监督的学习,观察有限数量的包含输入和预期输出的训练样本,不断调整网络内部节点之间的阈值和权重,最终形成对未知样本的预测能力。
本文选取与风电机组年发电量密切相关的机组参数,包括额定功率、风轮直径、叶尖线速度、设计叶尖速比、最大风能利用系数、切出风速、空气密度、年平均风速共8个变量作为网络的输入,结合相应的Bladed模型计算的年发电量作为网络的输出,形成网络的训练样本,并使用iSIGHT平台的优化算法,完成了风电机组设计年发电量预测模型。只要给出任意输入参数,即使没有任何相关的机组模型,也能够预测该机型的设计年发电量,或者通过期望的设计年发电量来反推机组参数。
BP神经网络建模
一、BP神经网络和Matalab实现
BP神经网络是一种按误差逆传播算法训练的多层前馈神经网络,是目前发展最成熟、应用最广泛的神经网络类型之一。该网络的特点是能够学习和存贮大量的输入输出模式映射关系,而无需事先描述这种映射关系的数学模型。通过反向传播来不断调整网络的权值和阈值,使得网络的误差平方和最小,从而实现输入和输出的非线性映射。BP神经网络模型拓扑结构一般包括输入层、隐层和输出层。如图1所示。
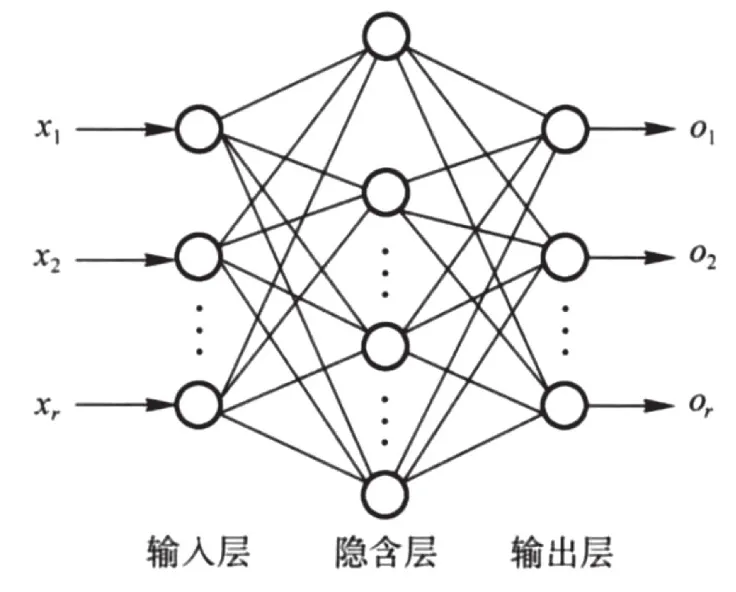
图1 BP神经网络基本结构
随着神经网络技术的发展,出现大量相关的建模仿真软件和仿真语言。本文所述的预测方法,使用MATLAB内置的神经网络工具箱实现。主要工作内容为网络输入输出参数的选择、网络结构特别是隐层数和隐层节点数的确定、网络性能的评价等方面。
二、输入和输出参数
风电机组的发电量与诸多因素有关,除了风电机组本身的设计规格之外,还与实际安装的风电场风能资源情况、机组故障率、控制策略等因素相关。由于本文的预测目标为设计年发电量,并考虑到训练和预测数据生成的效率,仅使用了静态功率曲线、标准瑞利分布计算的年发电量,应用到实际项目时,再附加上相应的折减系数。选择的网络输入参数,更多地反映了风电机组关键指标和风电叶片气动特性。
网络的输入参数,以及这些参数与发电量的关系简述如下:
(一)额定功率Pr
额定功率是风电机组最基本的参数之一。额定功率的增大,可以提升单台风电机组的年发电量。
(二)风轮直径RotorD
风轮直径同样是风电机组最基本的参数之一。风轮直径的增大,可以提升风电机组捕获风能的能力,特别是在低风速地区,效果更加明显。
(三)叶尖线速度Vtip
叶尖线速度在这里特指风电机组在额定转速下的叶尖线速度。适当地提高叶尖线速度,也就是提高额定转速,可以提升发电量。但由于叶尖噪音和叶片前缘风沙磨损的问题,叶尖线速度往往设定在75m/s-85m/s之间。
(四)叶尖速比TSR
叶尖速比在这里特指变速变桨风电机组在额定风速下,追踪最优Cp时的设计叶尖速比。在一定范围内,减小设计叶尖速比,会增大发电量,但同时会增大载荷和叶片成本。设计叶尖速比的确定,是综合考虑后的结果。
(五)最大风能利用系数Cpmax
风能利用系数是指风电机组将风能转化为电能的转换效率,最大风能利用系数是考虑不同叶尖速比和桨距角之后的最大值。最大风能利用系数的增大,风电机组的发电量也会相应增大。
(六)切出风速Vout
一般来说,风电机组的切出风速一般在20m/s-25m/ s之间。大风轮直径的风电机组,出于载荷的考虑,会将切出风速限制在较小的数值,这会造成一部分发电量的损失。但这些机组一般安装在低风速地区,切出风速区间所占的比例并不是很大,反映到发电量的损失一般可以接受。
(七)空气密度AirD
由于风能是空气流动产生的动能,动能与运动物体的质量有关,故空气密度也影响着发电量大小。较高的空气密度,会带来较大的发电量。
(八)年平均风速Vave
风速的变化,跟季节因素相关较大,所以年是较好的平均风速统计周期。年平均风速也可以用来反映风电机组整个寿命周期的平均风速。年平均风速较高时,会带来较大的发电量。
这里描述的8个与设计年发电量相关的参数,前6个是风电机组的本身属性,而后2个即空气密度、年平均风速是外部环境条件。
三、样本生成和归一化处理
本文利用现有的37个风电机组Bladed模型,额定功率涵盖1.5 MW-5.0MW,风轮直径涵盖88m-130m,计算了空气密度0.85 kg/m3-1.225kg/m3,年平均风速5m/ s-10m/s的机组年发电量,共形成了15873个训练样本。
为了测试网络的预测性能,特别是内插和外推性能,额外给出了7个机型的77个样本数据作为预测样本。这些样本的额定功率和风轮直径与训练样本有较大差异。
为了避免数据间数量级的差别影响结果,对训练数据进行了归一化处理,进行预测年发电量时,进行反归一化。
四、网络结构
网络结构分为三层,上文提到的8个风电机组参数作为输入层,年发电量作为唯一的输出层,输入层和输出层之间包含一个隐层,隐层节点数在3至14之间为宜。本文采用凑试法来确定隐层节点数,主要研究了5个至12个隐层节点数的预测情况,分别从预测精度、单调性、过拟合三个方面来确定网络结构。
五、预测精度
表1罗列了各个隐层节点数网络的预测精度,预测结果已经转化为与期望结果的百分比。
“预测平均值”是对77个预测结果的平均值,代表着预测的平均水平,越接近100%,代表预测越准确。“预测标准差”是对77个预测结果的标准差,代表着预测的稳定性。若标准差较大,则意味着有些样本预测得很准确,另外有些样本预测的偏差很大。由于Matlab随机给出网络的初始值,会造成最终网络性能差异,表中数值为5000个网络的平均值。
由表2可知,随着隐层节点数的增加,预测平均值有着接近100%的趋势,在隐层节点数7时-12时就逐渐稳定,预测标准差则逐渐下降,在隐层节点数11时处于较低点。从预测精度来看,隐层节点数11是较好的平衡点。
六、单调性
单调性是指最终网络应能表现出输入参数与输出参数的单调关系。以额定功率为例,在其他输入参数都保持恒定时,额定功率单调上升时,输出的年发电量应呈现单调上升趋势。表2列出了各个输入参数与输出参数应该呈现的单调关系。

表1 不同隐层节点数的预测精度
表2中的“↗”代表递增,“↘”代表递减。表中除了叶尖速比TSR应满足“递增-递减”关系之外,其他参数都符合“递增-递增”的单调关系。最好的情况是,网络能符合表2中所有的单调关系。但实际上训练后的大多数网络,是不能完全符合这些单调关系的。
图2绘制了编号为“net_Hid8_num74_00001111_ sum4”网络的单调性情况。编号名称中 “Hid8”表示这个网络有8个隐层节点,“num74”表生成的先后序列是第74个,“00001111_sum4”表示只有最大风能利用系数 Cpmax、切出风速 Vout、空气密度 AirD、年平均风速Vave这后面共4个参数才满足单调性关系。
由于Matlab随机给出了网络的初值,造成最终网络的不同单调表现,故可通过大量生成网络,加以分析和挑选。表3使用Matlab随机生成网络,每个隐层节点数的网络分别生成5000个,统计每个网络符合单调关系个数的总和,再按照隐层节点数分配到表中相应位置。
由表3可知,随着隐层节点数的增加,符合8、7、6、5个等较多单调关系的网络呈现递减趋势,符合单调预期的网络数量越来越少。在隐层节点数为5个时,5000个随机生成的网络中,还有36个网络全部满足单调关系,但到了隐层节点数10时-12时,只剩0个-2个了。
需要注意的是,在表3中隐层节点数11时,满足全部单调关系的网络个数为0,并不说明这样的网络结构就无法生成全部满足单调关系的网络,而只是因为比例所占极小,5000个网络的基数还远远不够。
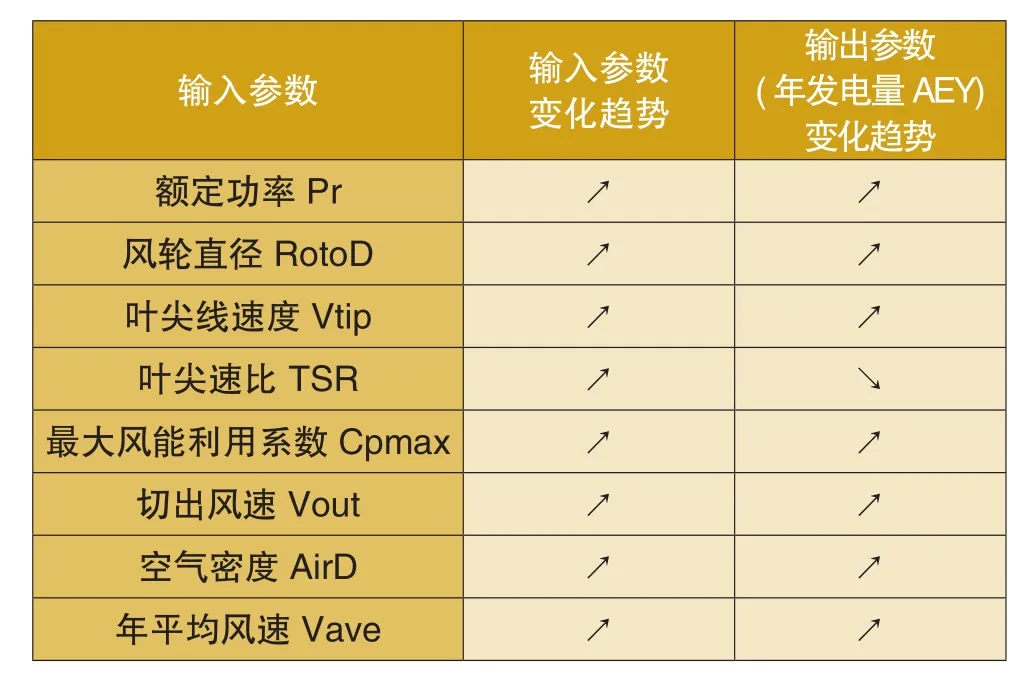
表2 输入和输出参数应符合的单调关系
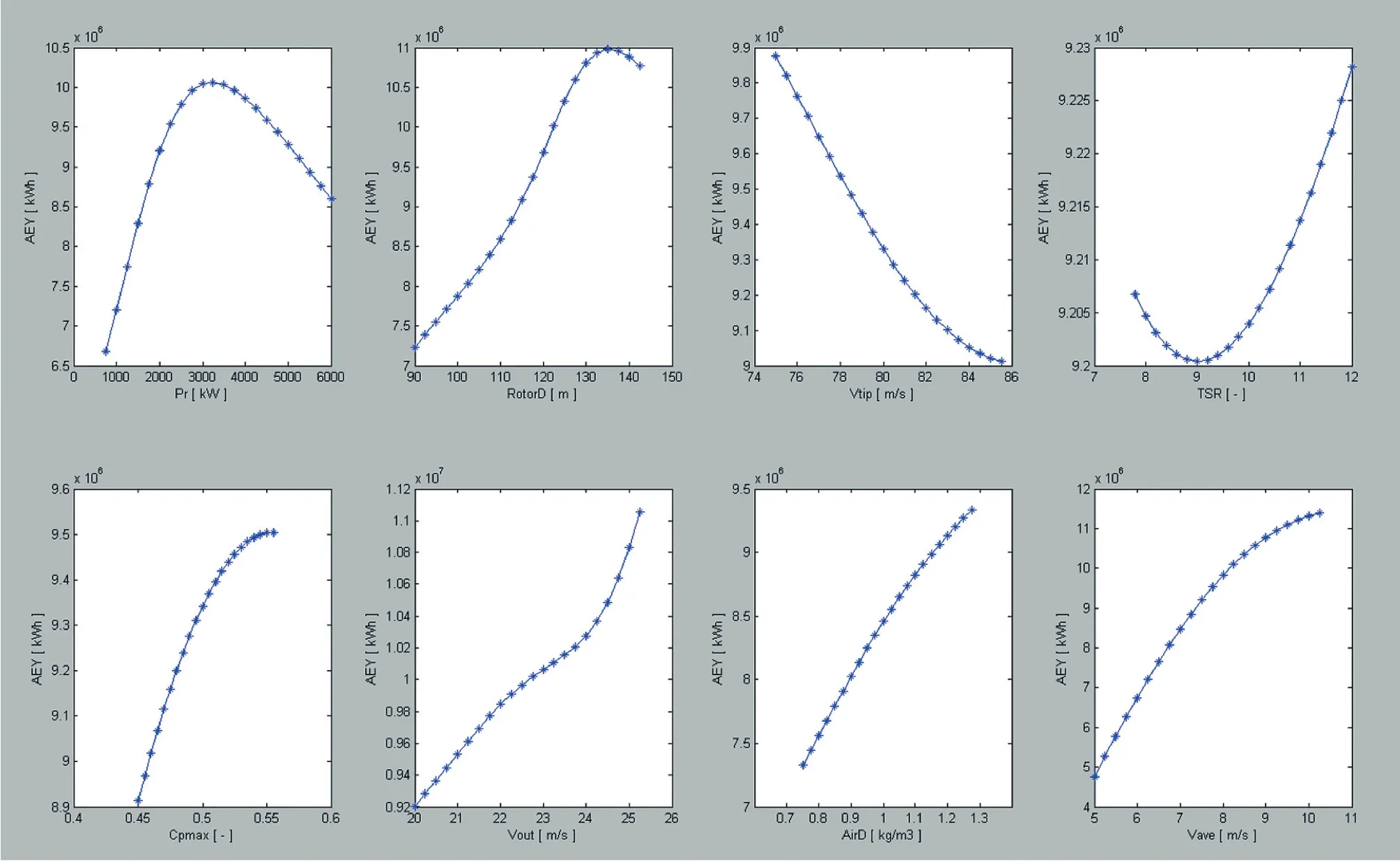
图2 网络net_Hid8_num74_00001111_sum4单调性情况
七、过拟合
进一步研究发现,除了网络的单调关系与隐层节点数有关,单调曲线的光滑程度与隐层节点数也有关系。
图3给出了编号为“net_Hid5_num672_11111111_ sum8”网络的单调表现,该网络为5个隐层节点数,所有的参数均满足表2的单调性关系,且曲线光滑均匀。
图4给出了编号为“net_Hid12_num1491_11111111_ sum8”的单调表现,该网络为12个隐层节点数,所有的参数也均满足表2的单调性关系,但曲线不太光滑,有较多的拐点变化。这很可能是网络在训练中,过分追求与样本的逼近程度,造成网络的过拟合。过拟合也会影响网络的泛化能力。
值得注意的是,本文并没有从理论上推导,这些输入参数与发电量的单调关系是否存在拐点。只是从过拟合的角度,期望最后的曲线应该是均匀变化的。
现将隐层节点数与网络性能的基本关系总结如下:隐层节点数较少时,满足单调关系的网络较多,曲线较为光滑,但预测精度总体较差;隐层节点数较多时,满足单调关系的网络较少,曲线也不太光滑,容易过拟合,但预测精度总体较好。
要想从预测精度、单调性、过拟合三者达到最佳平衡,隐层节点数11是较好的选择。但实际上在隐层节点数11时,5000个随机生成的网络,还找不到一个全部满足单调关系的网络,可见比例之小。即使找到了满足单调关系的网络,在较大的隐层节点数的前提下,期望单调曲线光滑,不出现凹凸变化,也是一件小概率事件。只使用大量随机生成,并加以筛选的方法,很难得到理想性能的网络。

表3 不同隐层节点数网络的单调关系统计
图3 网络net_Hid5_num672_11111111_sum8单调性情况
八、iSIGHT平台优化网络初始权值和阈值
实践证明,使用优化算法和BP神经网络结合的方法,可以较好地获得预期性能的网络。iSIGHT平台内置多种成熟的优化算法,提供多种满足约束条件和目标函数的设计方案,并支持多种CAD和CAE商用软件的接口,可以直接调用Matlab程序,是优化网络性能的较好途径。具体方法如下:
(一)确定iSIGHT输入变量。该网络结构为8个输入参数、11个隐层节点数、1个输出参数,包含99个权值、12个阈值共111个初始变量,作为iSIGHT的输入变量。
(二)确定iSIGHT输出变量。该网络的评价指标分三个方面,预测精度方面有预测平均值、预测标准差、预测极差,单调性方面为单调关系个数,过拟合方面将统计单调曲线无拐点的个数。综上iSIGHT共包含了5个输出变量。
(三)确定iSIGHT的约束和目标。单调关系个数要求必须全部满足,即单调关系个数限制为8。预测平均值目标为1,即希望预测平均值尽可能接近1。预测标准差和预测极差最小化,即希望预测的稳定性要非常好。无拐点数最大化,即希望单调曲线尽可能均匀变化。
(四)确定iSIGHT的优化算法。综合考虑优化问题的多目标性、不连续性、非线性的特征,加上单次计算时间不是很长,故采用了AMGA优化算法,进行了5000次的迭代。图5是优化完成后的网络单调性情况。
由图5可见,优化后的网络曲线全部满足了单调关系,且变化光滑均匀,基本无明显的拐点变化。由表4可知该优化网络的预测平均值为100.8%,预测标准差为0.0143,预测极差在9.7% 以内,可见最终的优化网络,较好满足了单调性、过拟合、预测精度三方面的要求。
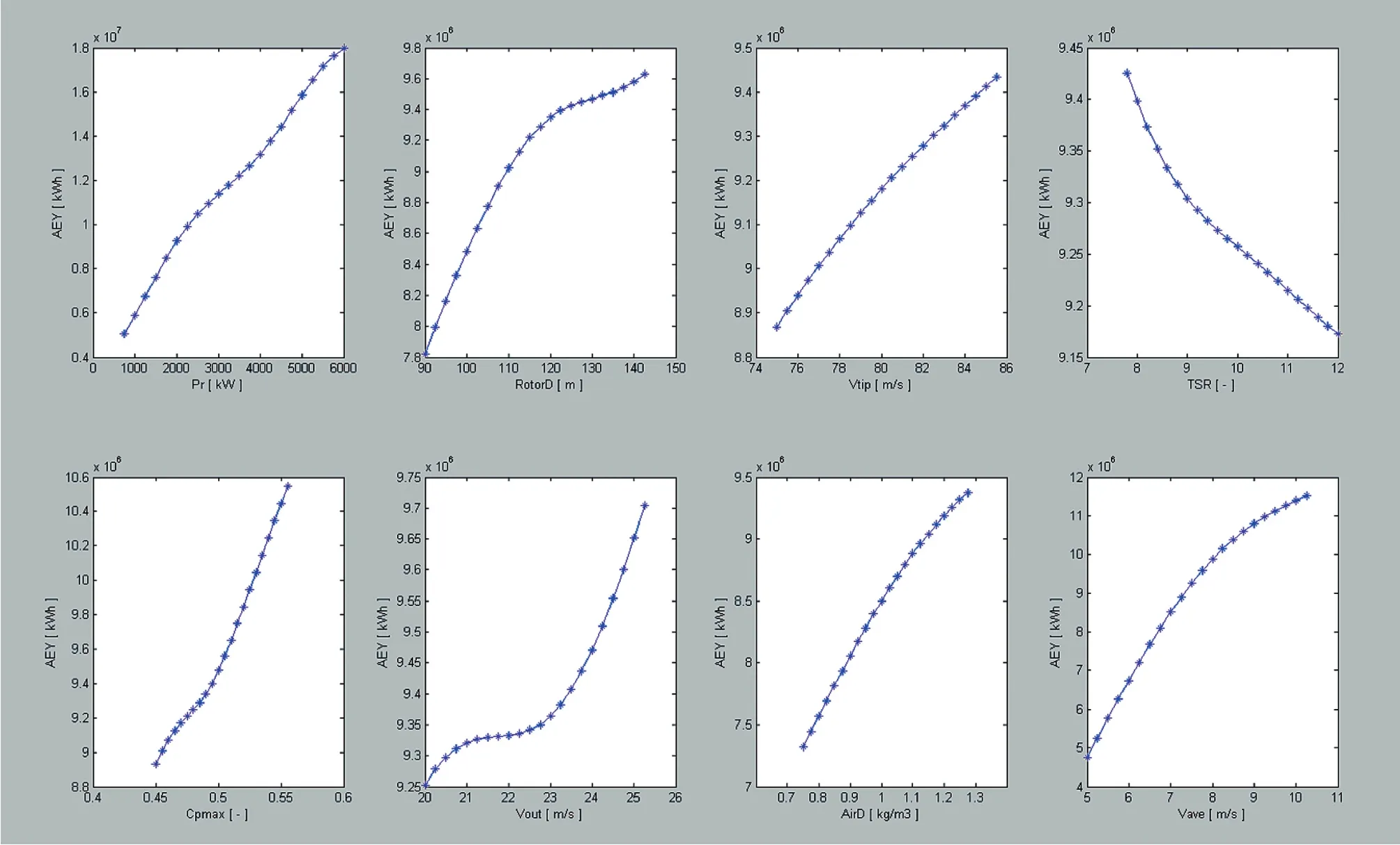
图4 网络net_Hid12_num1491_11111111_sum8单调性情况
实例应用
如上所述,最终网络已经较好地完成了风电机组发电量的预测功能。但实际工作中,有时并不需要发电量的预测,而是去寻求什么样的机型、什么样的风能资源条件,能够满足某种发电量的心理预期。这便是现有预测的逆问题。为了解决这个问题,当然可以把样本数据的输入输出做一下置换,再进行训练、筛选、评价和优化。这无疑需要巨大和重复的工作量,而且在实际问题提出前,哪些参数为输入,哪些参数为输出,还非常不确定。为了解决这个问题,同样可以用iSIGHT进行反推和优化。
以开发一款3.0MW机型为例,目标风电场空气密度1.0kg/m3,年平均风速6.5m/s,在发电折减系数75%时,期望达到的全年可利用小时数为2200h,求最小的风轮直径。假定最大风能利用系数0.48、叶尖速比10.5、切出风速20m/s、设计叶尖线速度80m/s,iSIGHT给出的风轮直径为128.4m。
这其实是一个已知输入输出参数之间映射关系,以风轮直径为目标解的问题,相当于解方程。实际上iSIGHT可以利用这个映射模型,设置更多的变量、约束和目标,得到更多更有价值的应用。
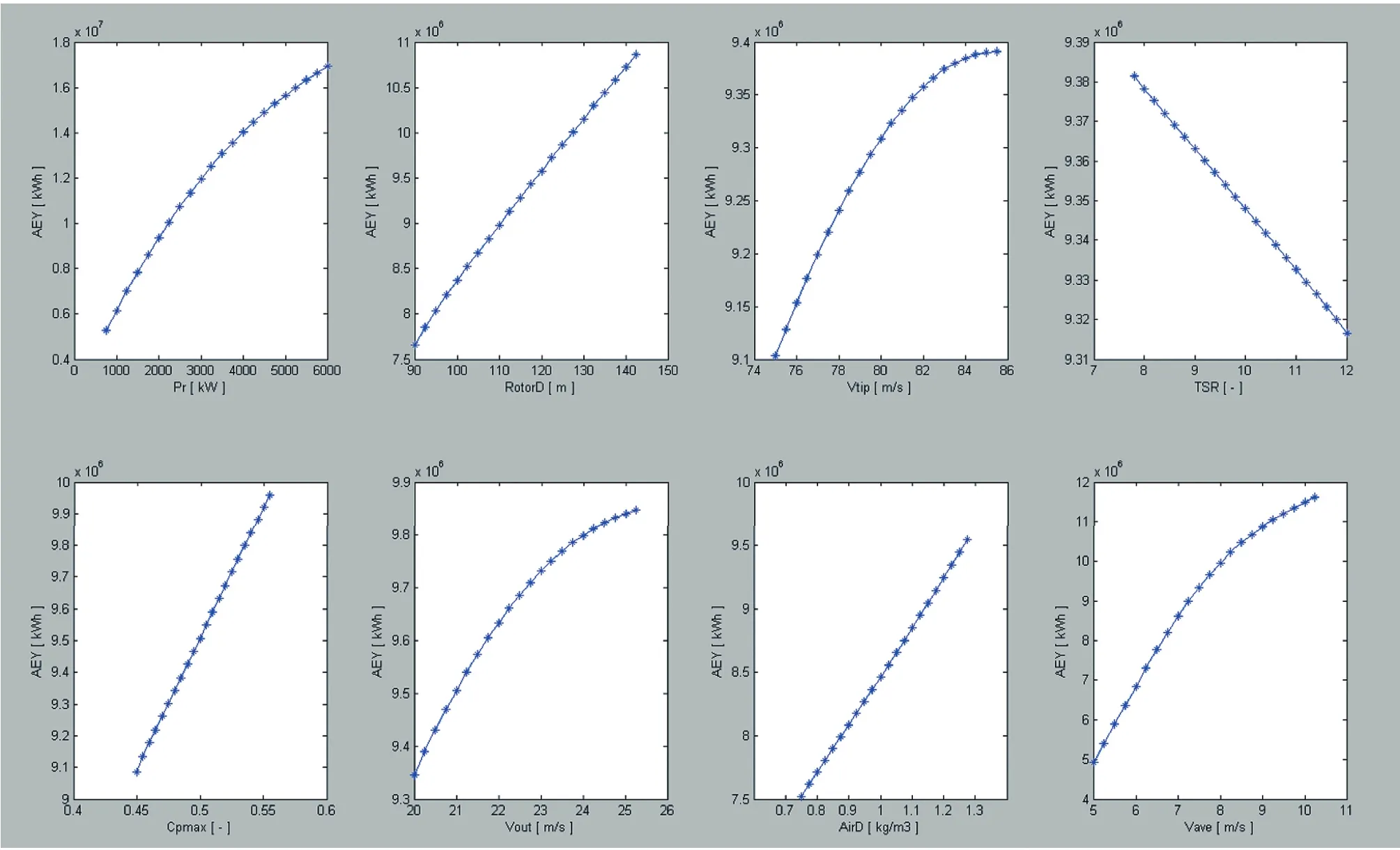
图5 进行iSIGHT优化后的网络单调性情况

表4 单一网络与优化网络预测精度对比
结论
本文依照神经网络的基本原理,以风电机组与发电量相关参数为输入,建立BP神经网络模型,并考虑了单调性、过拟合、预测精度三方面,使用iSIGHT平台对现有的网络进行了优化。结果表明,该方法对风电机组设计年发电量有较好的预测性能。为了进一步提高预测模型的实用性,使用iSIGHT平台完成了各参数的反推和优化。
本文提供的方法在风电叶片开发、目标风电场的风电机组选型、风电机组新品预研等方面有着重要的参考和指导价值。
(作者单位:浙江运达风电股份有限公司)

