金沙江白鹤滩水电站岩体变形特性动静对比研究

黄火林 李广场 徐福斌

金沙江白鹤滩水电站岩体变形特性动静对比研究

黄火林 李广场 徐福斌

（浙江华东工程安全技术有限公司 浙江杭州 310014）

大型水电工程研究岩体变形特性的动静对比关系具有重要的意义，其成果可为了解工程岩体特性、岩体质量分级、稳定性评价、变模分区、建基面施工验收提供技术支撑。本文基于白鹤滩水电站可研阶段的岩体动静参数测试成果，分析测试成果的规律性，结合白鹤滩岩体的岩性多样性、各向异性、非均质性等特征，选择具有地质代表性的试验点进行动静对比关系式拟合，建立了地震波速度、声波速度与岩体变形模量之间的关系，并通过分析论证，推荐使用声波速度与岩体变形模量的动静对比关系式。

白鹤滩水电站 动静对比 变形特性 变形模量 波速

前言

金沙江白鹤滩水电站位于金沙江下游河段，坝址左岸属四川省宁南县跑马乡，右岸属云南省巧家县交界大寨镇。白鹤滩水电站是我国继三峡、溪洛渡之后又一座千万千瓦级的水电站。

岩体变形特性的动静对比关系式研究对大型水电工程具有重要的意义，其成果可为了解工程岩体特性、岩体质量分级、稳定性评价、变模分区、建基面施工验收等提供技术支撑。国内各大中型水电站都开展了动静对比研究工作，如三峡、溪洛渡、二滩、锦屏等。白鹤滩作为国内又一座大型水电站，开展动静对比研究具有重要性和必要性。

国外在20世纪30年代开始了岩体动静关系的研究工作，国内从20世纪80年代开始研究工作。李泽、钱世龙从弹性理论出发，提出动、静弹模在本质上是一致的，两者所存在的差异是由于动力法和静力法本身技术条件（或手段）造成的，对比是有条件的，动静弹模测试方法各有优势。沙椿通过静动对比，分别建立变形模量与声波和地震波速度的相关规律，并将大量的弹性波测试成果转换为变形模量，为坝基岩体质量分级、稳定性评价及变模分区、应力分析提供了实用指标。李维树对三峡坝区岩体及乌江构皮滩水电站分别进行了动力法和静力法的试验数据研究，建立坝区变形特性的动静对比相关式。全海通过对岩体变形模量与原位纵波波速的研究，结合工程实例，建立了该工程岩体变形模量与声速的相关关系。胡国忠、王宏图以川东北飞仙关组的储层和致密层岩石为研究对象，建立不同岩性的岩石的动弹性模量和静弹性模量的相关关系。李伟、田连义分别对小湾水电站坝址区岩体的动静弹模进行对比分析研究，通过动静对比关系将岩体弹性波测试的速度空间分布规律转换为变形模量分区，也为工程设计及坝基岩体质量提供科学依据。

从国内动静对比研究成果来看，各水电工程所采用的动静对比关系式各异，这也体现了各水电站地质条件的差异性以及动静对比研究的复杂性。本文基于白鹤滩水电站可研阶段的岩体动静参数测试成果，分析测试成果的规律性，结合白鹤滩岩体的岩性多样性、各向异性、非均质性等特征，选择具有地质代表性的试验点进行动静对比关系式拟合，建立了地震波速度、声波速度与岩体变形模量之间的关系，并通过分析论证，推荐使用声波速度与岩体变形模量的动静对比关系式。

1 测试方法

1.1岩体变形试验

岩体变形试验采用刚性承压板法，同时在试点周边钻取4～8个声波孔，进行声波测试。

岩体变形模量或者弹性模量按公式（1）计算，当以全变形W0代入式中计算时为变形模量E0；当以弹性变形We代入式中计算时为弹性模量Ee。

式中：W为岩体表面变形；P为按承压面单位面积计算的压力；D为承压板直径；μ泊松比。

1.2弹性波测试

针对变形试验点岩体开展了声波和地震波测试，测试方法和资料整理如下。

1.2.1 声波测试

变形试验点岩体声波速度测试采用RS-ST01C智能型声波仪。本次采用单孔声波测试法，声波速度的计算公式如下：

式中：t1，t2分别为同一激发信号的相同相位在两个接收换能器的接收时间；Δt为二者时间差；L为两个接收换能器的间距；Vp为声波速度。

1.2.2 地震波测试

平洞洞壁岩体和变形试验点岩体地震波测试使用美国公司制造的SE12型智能地震仪及其配套设备。

变形试验点岩体地震波测试时，检波器以变形试验点为中心两边展开布置，对于平洞洞壁岩体检波器沿洞壁呈直线布置。采用相遇观测系统，以锤击作震源，道间距为0.5～1m，地震波测试使用同一仪器和检波器，每次测试时使用同一采集参数。

从地震波原始记录上读取纵、横波旅行时，然后求取θ（x）曲线，利用下式计算波速：

式中：v为地震波速度；△s为θ(x)曲线的距离差。

2 测试成果

预可至可研阶段白鹤滩坝区共完成162点玄武岩刚性承压板试验，其中134个变形试验点进行了波速测试，并取得有效数据；试验压力为水平向试验点计73点，压力为铅直向试验点计61点。根据变形试验成果对各岩性变模进行统计，结果见表1。

从统计成果可知：

（1）同岩性岩体，随着岩体类别的提高，其变模和波速增高。

（2）对比同类别岩体的变模，隐晶质玄武岩、杏仁状玄武岩和角砾熔岩间差异较小，将它们归并为同一类岩体，统称为非柱状节理玄武岩。除Ⅲ2岩体外，大部分同类别柱状节理玄武岩的变模与非柱状节理玄武岩相当，但波速高于非柱状节理玄武岩。

（3）对具有统计意义的岩体类别（至少有3点）而言，大部分同类岩体压力水平向变模高于铅直向，说明岩体具有各向异性特征。

3 动静对比分析

从第2节的分析可知，柱状节理玄武岩与非柱状节理玄武岩动静参数之间存在差异，因此在分析中将二者分别进行动静参数关系拟合。考虑试验点的地质代表性、匹配性、规律性等因素，剔除了部分试验点数据。

3.1地震波速度与变模相关性

地震波只进行水平向测试，分别对柱状节理玄武岩与非柱状节理玄武岩体的地震波速度与变模之间进行动静对比关系曲线拟合，关系式分别为E0=7.9366·Vp0.4709和E0=1.4399Vp1.6968，其相关系数分别为0.24和0.53。可见地震波速度与变形模量之间相关度低。

3.2声波速度与变模相关性

对134个刚性承压板变形试验点的岩体测得了声波速度，其中试验压力水平向试验点为73点，压力铅直向试验点为61点，根据上文所述，将其分为柱状节理玄武岩岩体与非柱状节理玄武岩岩体，并考虑水平向与铅直向变形模量的差异，再分压力方向进行声波速度与变形模量的关系拟合。

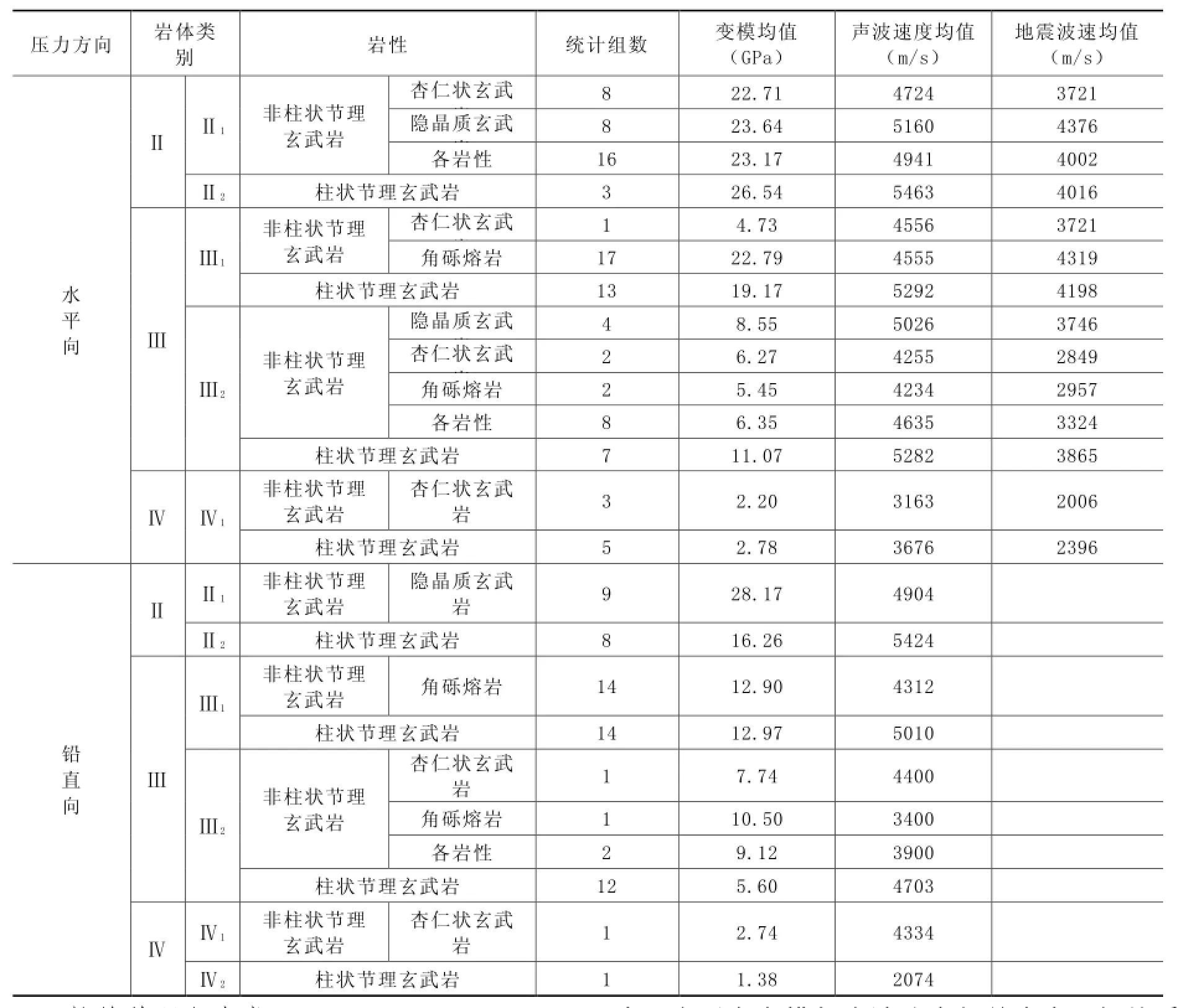
表1 刚性承压板变形试验成果统计一览表

3.2.1 柱状节理玄武岩

柱状节理玄武岩体声波速度和变形模量关系拟合中，水平向采用了23组数据，铅直向采用了14组数据，其拟合关系式分别为E0=0.0264e1.2232Vp和E0=0.1075e0.9337Vp，其相关系数分别为0.96和0.84。由此可知，柱状节理玄武岩体的水平向变模和铅直向变模与声波速度相关度高。因此，考虑将其二者进行归并拟合，拟合曲线关系式为E0=0.0344e1.1667Vp，柱状节理玄武岩体水平向和铅直向动静参数进行归并拟合后，相关度高，相关系数达到0.94。

3.2.2 非柱状节理玄武岩

非柱状节理玄武岩体声波速度和变形模量关系拟合中，水平向采用了31组数据，铅直向采用了23组数据，其拟合关系式分别为E0=0.0474e1.2191Vp和E0=0.6214e0.6928Vp，相关系数分别为0.90和0.54。

由以上分析可知，对非柱状节理玄武岩体而言，水平向变模与声波速度相关度高，相关系数为0.90，而铅直向变模与声波速度相关程度则要低，相关系数仅有0.54。

4 动静对比关系式论证与推荐

前述章节建立了各岩性岩体地震波、声波与模量的相关关系，各动静对比关系式是否符合实际需要进一步分析和论证。动静对比关系式拟从以下两个方面进行评价：

（1）相关系数。相关系数表征两个变量的相关程度，相关系数越大，表明两变量的相关性越好，通常相关系数大于0.8时认为两变量的相关性较好。由于白鹤滩坝区地质条件的复杂性，相关系数按表2的标准评价动静对比关系式的相关程度。

（2）相关资料论证。以波速标准值验算模量，将其与变模标准值进行对比，分析动静对比关系式的合理性和适用性。

表2 动静对比关系式相关程度评价表

4.1地震波速度与变形模量

各岩性岩体刚性承压板模量和地震波速度的动静对比关系式汇总见表3。

表3 动静对比相关性一览表

从表3中可知，岩体地震波速度与变形模量拟合关系式的相关系数均小于0.6，相关性差，不予采用该动静对比关系式。

4.2声波速度与变形模量

各岩性岩体刚性承压板模量和声波速度的动静对比关系式汇总见表4。以下分别对柱状节理玄武岩和非柱状节理玄武岩的动静对比关系式进行分析与评价。

4.2.1 柱状节理玄武岩

从表4可知，柱状节理玄武岩压力水平向、铅直向和综合水平铅直方向的动静对比关系式均为指数函数，相关系数均大于0.8，相关性较好至好。

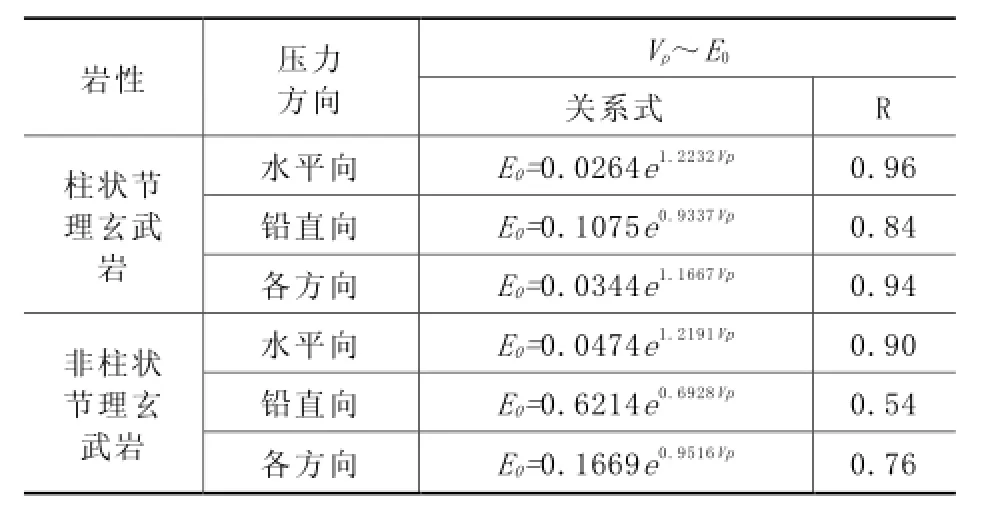
表4 动静对比相关性一览表

根据Vp～E0关系计算出各类柱状节理玄武岩波速标准值所对应的变模，计算值与变模标准值对比见表5。

由表5可知：（1）根据水平向、铅直向和综合Vp～E0关系式计算的各类岩体变模相近；（2）依据Vp～E0关系式计算的各类岩体变模与水平向变模标准值相近，大于铅直向标准值。

表5 柱状节理玄武岩各类变模对比一览表

变形模量标准值的水平向和铅直向存在差异，这是由于层间、层内错动带影响以及岩体松弛程度不同所造成的，而从声波速度测试成果来看，声波并不具有各向异性特征，因此通过Vp～E0关系式所得的水平向与铅直向变模相近，这也论证了成果的合理性。

4.2.2 非柱状节理玄武岩

非柱状节理玄武岩Vp～E0关系均为指数函数，压力水平向的Vp～E0相关系数为0.9，相关性好。铅直向和综合向的Vp～E0相关系数范围为0.54～0.76，相关性差到一般。

根据Vp～E0关系计算各类非柱状节理玄武岩波速标准值所对应的变模，计算结果与变模标准值对比见表6。

表6 非柱状节理玄武岩各类变模对比一览表

从表6中可知：

（1）除Ⅳ类岩体外，根据水平向、铅直向和综合Vp～E0关系式计算的各类岩体变模相近；

（2）依据Vp～E0关系式计算的各类岩体变模与水平向变模标准值相近，铅直向计算成果则大部分大于变模标准值。

4.3动静对比关系式推荐

基于本文提出的两个标准，上述分别对柱状节理玄武岩与非柱状节理玄武岩进行动静对比关系式论证分析。从论证成果可知，柱状节理玄武岩体水平向与铅直向动静对比关系式皆合理，且二者较为相近，因此推荐综合Vp～E0关系式；对非柱状节理玄武岩体而言，水平向Vp～E0关系式相关性好，且成果合理，而铅直向Vp～E0关系式则相关性差，且与相应的变模标准值之间存在差异，因此推荐水平向Vp～E0关系式，考虑到波速无各向异性特征，水平向与铅直向推荐同一个关系式。推荐的Vp～E0关系式见表7。

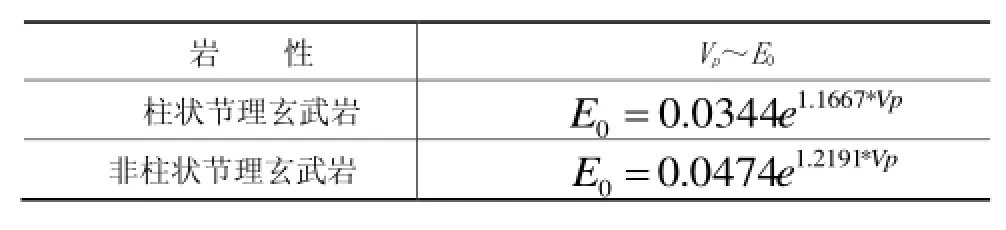
表7 推荐的动静对比关系式汇总表

5 结论

（1）基于白鹤滩岩体弹性波和变形特性，将隐晶质玄武岩、杏仁状玄武岩和角砾熔岩归并为非柱状节理玄武岩，动静对比关系按柱状节理玄武岩和非柱状节理玄武岩分别建立。

（2）各岩性岩体地震波速度与变模、静弹模的相关性差，无法建立相关性较高的动静对比关系式，主要原因为变形试验和地震波测试反映的岩体不一致。

（3）柱状节理玄武岩刚性承压板水平向、铅直向、综合水平铅直向动静对比关系式相近，均呈指数函数，相关程度较高，且与相应的变模标准值接近。推荐刚性承压板综合Vp～E0关系式作为动静对比关系式。

（4）非柱状节理玄武岩各模量和声波速度呈指数相关，水平向的Vp～E0关系相关度高，铅直向Vp～E0关系相关度低，故推荐刚性承压板水平向Vp～E0关系式作为非柱状节理玄武岩的动静对比关系式。

（5）推荐的各动静对比关系式依据可行性研究阶段的测试资料，随着工作的深入和资料的补充，动静对比关系式需进一步验证与完善。

1 林英松, 葛洪魁. 岩石动静力学参数的试验研究[J]. 岩石力学与工程学报，1998，17（2）：216-222.

2 李泽, 钱世龙.岩体动弹性模量测试动静弹性模量对比探讨[J]. 工程物探，

3 沙椿. 工程岩体力学试验中的静动对比[J]. 工程物探，2003（1）：3-6.

4 李维树. 三峡工程坝区岩体变形特性的动静对比分析[J].长江科学院院报，1995，12（4）：44-50.

5 李维树，鲁先元. 三峡工程坝区工程岩体变形参数的动静特性研究[J]. 地下空间，1999，19（4）：332-337.

6 李维树, 周火明. 确定工程岩体宏观变形参数的方法探讨[J].岩石力学与工程学报, 2001, 20（增）：1758-1761.

7 李维树, 彭朝全. 地下洞室群岩体变形参数取值研究[J].岩石力学与工程学报, 2004, 23(增2):4916-4920.

8 全海. 岩体变形模量与声速关系探讨[J]. 第八次全国岩石力学与工程学术大会论文集, 2004：970-973.

9 胡国忠, 王宏图. 岩石的动静弹性模量的关系[J]. 重庆大学学报(自然科学版), 2005, 28（3）：102-105.

10 李伟, 沈蓉. 小湾水电站坝址区岩体变形特性研究[J].第一届中国水利水电岩土力学与工程学术讨论会论文集, 2006：87-89.

11 田连义, 李维耿. 工程岩体力学试验中的动静对比在小湾水电工程中的应用[J]. 工程地球物理学报, 2009，6（S1）：145-148.

10.3969/j.issn.1672-2469.2014.02.027

TV221.2

B

1672-2469（2014）02-0098-05

黄火林（1982年- ），男，工程师。