Hilbert-Huang 变换应用于高压输电线路故障测距
尔晨希,付周兴
(西安科技大学 电气与控制工程学院,陕西 西安710054)
0 引言
高压输电线路对电力系统的运行有着重大的意义。很多连锁故障的发生是由于未能及时排除线路故障而引发的,从而对电力系统产生了巨大危害。采取有效的措施对输电线路进行故障定位显得十分重要。准确快速地进行故障定位,有助于工作人员迅速查找故障点,减少工作强度,提高电力系统的稳定性,促进电网的安全运行。
目前,小波法[1~3]和数学形态学方法[4~5]等被国内外广泛应用于行波故障测距中。小波分析结果受到了小波基的种类、采样率及分解尺度等因素的影响。在实际工程中,如何选择合适的小波基和分解尺度并不容易;而且,一旦选择了小波基和分解尺度,所得到的结果是某一固定频率段的信号,这一频率段只与信号的采样频率有关,而与信号本身无关。从这一点上来说,小波分析不具有自适应性,并不能真实反映信号的特征[6~7]。数学形态学用在测距上,结构元素理论上还没有选取原则,不同的结构元素测距结果相差往往较大;而且,一个结构元素在此处变换最优,在彼处不一定最优[8]。
据此,针对上述传统行波法的弊端,提出了将Hilbert-Huang 变换应用于故障测距。Hilbert-Huang 变换法可以高效处理非线性非平稳信号,其首先采用EMD 方法将信号分解为若干个固有模态函数(简称IMF)之和,然后对每个IMF 分量进行Hilbert 变换得到瞬时频率和瞬时幅值。这是一种直接从信号本身获得基函数的方法,避免了小波基选取困难的问题,具有自适应性;其可以实现从低频信号中分辨出奇异信号。另外,基于Hilbert-Huang 变换的故障测距区别于小波变换法,不受测不准原理的制约,可以达到更高的故障测距精度。
1 Hilbert-Huang 变换
Hilbert-Huang 变 换[9](Hilbert-Huang transform,HHT)信号分析法可分为经验模态分解(empirical mode decomposition,EMD)和Hilbert 变换两个步骤。
1.1 经验模态分解(EMD)
HHT 的核心部分为经验模态分解EMD。EMD本质上就是将一个非平稳信号分解为若干个具有合理的瞬时频率定义特点的本征模态函数IMF(intrinsic mode function,IMF),各阶IMF 需要满足一定的条件。然后对IMF 进行Hilbert 变换,得到每一个IMF 的随时间变换的瞬时频率和瞬时幅值,由此可以构建信号的时间—频率—能量分布。
EMD 的分解是一个逐步筛选的过程,其具体分解步骤是:对任意一个实信号s(t),首先用s(t)的所有极大值点和极小值点确定出s(t)的上下包络线。计算出它们的平均值曲线m1(t),用s(t)减去m1(t)得

理想情况下,h1(t)应该是一个IMF;但是为了不遗漏新的极值点,把h1(t)作为原信号,重复上面所介绍的步骤,反复筛选得到:

反复筛选k 次后,h1,k(t)成为一个IMF,即

c1(t)应包含信号中周期最短的分量。从原信号中减去c1(t)得第一阶剩余信号:
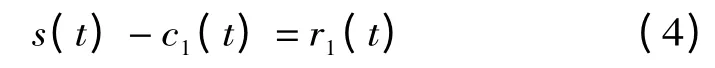
同理,把后面的r1(t),r2(t),…,ri(t)作为新的信号重复以上过程依次得到各IMF 和剩余信号:
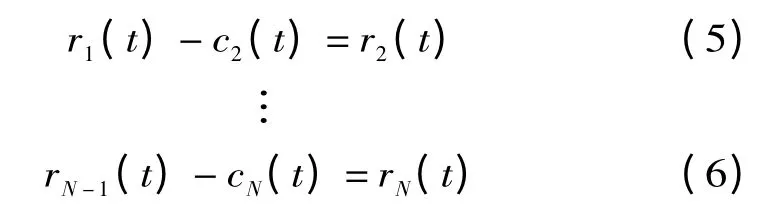
综合上述公式得:
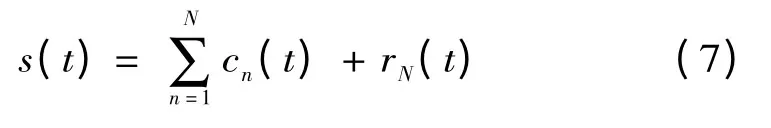
即可得到各阶c1,c2,…各阶IMF。
由于大多数信号或数据不是IMF,因此不能直接进行Hilbert 变换。一个IMF 函数应满足以下两个条件:
(1)在整个数据序列中,极值点的数量与过零点的数量必须相等,或最多相差不能多于一个。
(2)在任一时间点上,信号的局部极大值和局部极小值定义的包络平均值为零。
1.2 Hilbert 变换
给定一个连续的时间信号X (t),则其Hilbert 变换定义为:

定义Z(t)=X(t)+jY(t)=a(t)ejθ(t)为信号X(t)的解析信号;其中a(t)为瞬时幅值,a(t)=(t)+Y2(t);θ (t)为瞬时相位,θ (t)=arctan。
信号的瞬时频率可通过以下式求得:

信号通过HHT 一旦分解完毕,可根据工程问题的要求灵活实现重构。Hilbert 谱能够更好地反映出信号内在本质特征。
2 行波测距的原理
行波法进行故障测距,采用输电线路故障后的行波,利用行波折反射的特点可以精确地计算出故障距离;分为单端法和双端法 (详见文献[10,12])。
高压输电线路发生故障时,故障点产生的电流、电压行波将向线路两端传输。检测系统采集到的三相电压、电流信号并不独立,不能直接对其进行分析。首先需要去掉电磁耦合,对行波信号进行相模变换。经过相模变换可以将不独立的相分量变成各相独立的模分量。常用的一个方法就是凯伦贝尔(Karrenbauer)变换[11],其变换矩阵结构简单,相电流和模电流之间的关系为:
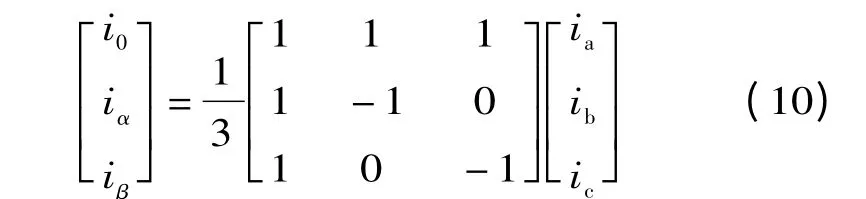
α,β 模电流分量分别为:

经过凯伦贝尔变换,可以得到线路的0 模分量、α 模分量、β 模分量。0 模分量为相与大地之间运动的波,其波速并不稳定,并且在运动过程中损耗较大。α 模分量、β 模分量为在相间运动行波,波速具有确定性。因此,选择α 模分量、β模分量实现故障测距。
3 Hilbert-Huang 变换故障测距方案
用Hilbert-Huang 方法判断故障测距时,行波到达时间以及步骤如下:
(1)输电线路发生故障时,由故障点发出的电流、电压信号向输电线路两端传播,其行波传播波头包含高频暂态分量。当线路两端的行波采集处理系统感应到高频信号时,标志着行波到达线路一端。
(2)对行波进行去除噪声的处理。进行凯伦贝尔相模变换以去除各相电流、电压之间的耦合,得到行波的线模分量。
(3)对行波线模分量进行EMD 分解,对信号逐级筛选得到各阶IMF。由于第一阶IMF 的能量最大,频率变化较为明显,对IMF1 进行Hilbert变换,得到瞬时时频图。故障行波在瞬时时频图中表现为高频率的突变,可以清晰地在图中看到行波波头到达线路一端的时间。
(4)查找计算行波波速,采用单端或者双端法计算故障点的具体位置。单端法和双端法(参见文献[9,11])的计算公式分别为:

式中:l1为所测得的故障距离;l 为线路全长;v为行波波速;式(13)中t1,t2分别代表行波第一次到达测量端的时间、故障点反射波到达测量端的时间;式(14)中t1,t2之差代表故障行波波头到达线路两端的时间差。采用Hilbert-Huang变换的故障测距流程图如图1 所示。

图1 HHT 故障测距方案流程图
4 小波分析法与Hilbert-Huang 变换法的对比
从具有自适应性的方面讲,小波变换需要预先选定一个满足“可容性”条件的小波基。在实际工程中,选择不同的小波基会产生不同的测距结果,选择出一个最合适的小波基并非易事。HHT 通过逐次筛选,得到的各阶IMF 即为自适应产生的“基”,不同的行波信号的基是相异的,具有自适应性。另外,小波变换对行波信号分析的结果是通过基函数的卷积产生的。HHT 产生的频率是对信号的相位函数瞬时求导产生,具有局部性的特征。
从行波信号源方面讲,理论上小波变换可以分析非线性非平稳信号,但在实际工程中,其只能分析线性非平稳信号。且由于其时间窗口和频率窗口的乘积为一个常数,受到Heisenberg 测不准原理的制约,使基于小波变换的测距精度受到了限制。HHT 不同于小波变换,是严格意义上的可以分析非线性非平稳信号的方法,使可以用HHT 处理的信号范围变得更广;且由于其通过瞬时求导产生频率的方法,更适合处理突变信号。表1 从几个方面对比了小波变换和HHT。
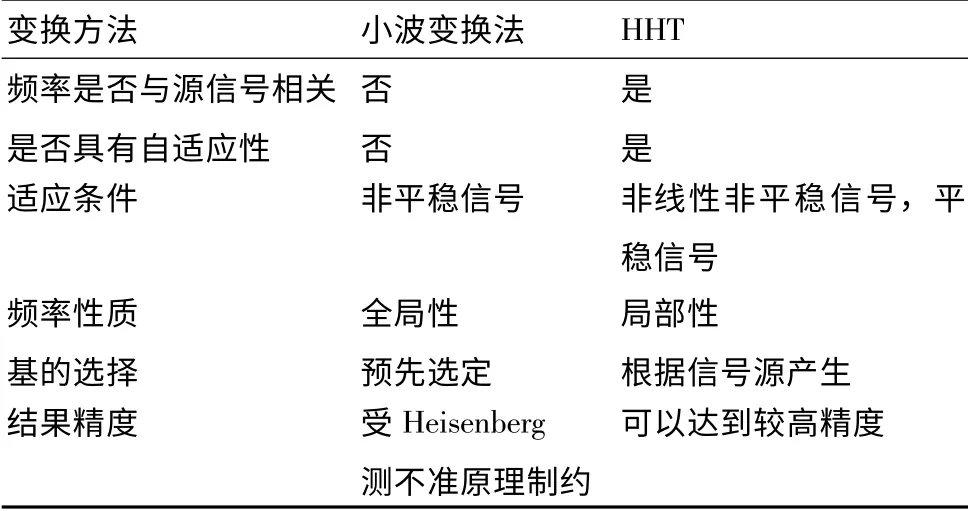
表1 小波变换和HHT 的对比
5 仿真算例分析
本文采用电磁暂态程序(EMTP)对500 kV双端电源输电系统进行仿真,仿真模型如图2 所示。线路全长为250 km,电源频率为50 Hz,A 相在30 ms 时经电阻接地。仿真时间为50 ms。左端电源电势=612.3 kV,右端电源电势=612.3∠15 kV。单位长度线路正序、零序电阻分别为R1=0.027 Ω/km,R0=0.194 8 Ω/km;单位长度线路正序、零序电感分别为L1=0.886 3 mH/km,L0=2.068 mH/km;单位长度线路正序、零序电容分别为C1= 0.012 7 μF/km,C0= 0.009 μF/km。通过仿真得到故障前后电压电流波形。采用Matlab 软件对波形进行相模变换,EMD 分解,Hilbert 变换,对故障初始行波和故障点反射波到达时间进行识别。仿真结果如图3,4 所示。
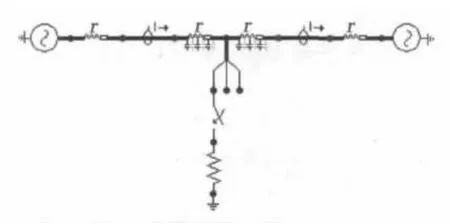
图2 双端电源输电系统模型
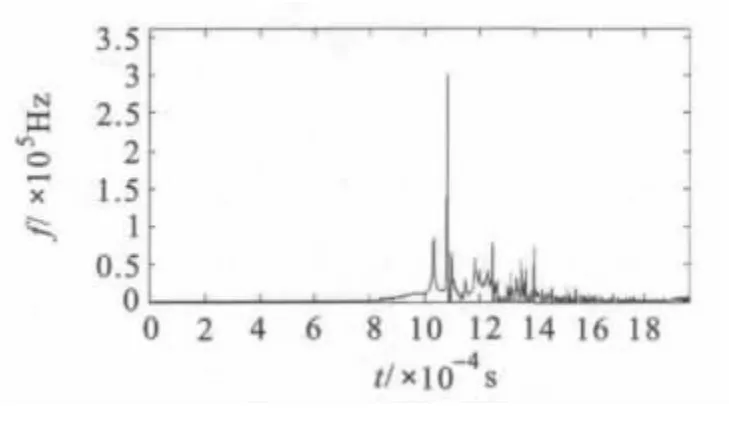
图3 IMF1 分量瞬时频率
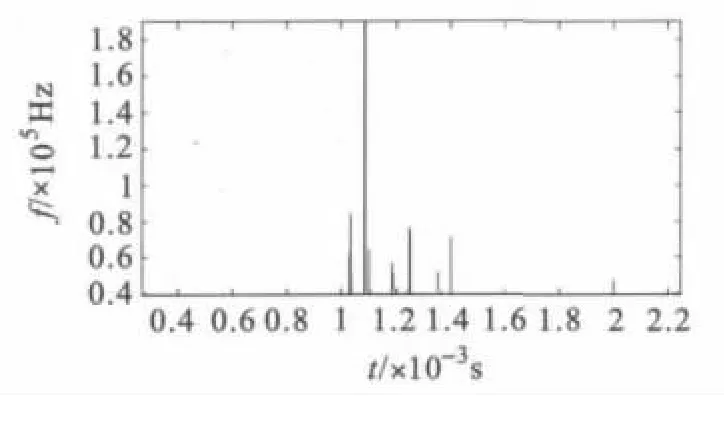
图4 IMF1 分量瞬时频率图局部放大图
同时本文选取db4 小波基进行5 层离散小波变换,使用第一层细节分量计算故障点距离,如图5,6 所示,并将所测结果与HHT 计算的结果进行对比。
图4 中,故障点行波频率突变明显,可以清晰地找出行波到达以及反射时间。可以证明HHT方法有效。模型以故障定位装置放在左侧进行仿真,0.03 s 时距离左侧75 km 处发生A 相接地故障,取IMF1 来确定行波波头。从图中可以看出,第一个脉冲为初始行波,所对应的时间为1.032 ms,第二个脉冲为故障点反射波,所对应的时间为1.082 3 ms,行波波速为2.98 ×108m/s,代入单端法故障测距公式后得故障距离左端74.947 km,误差为-53 m,所测结果较为精确。
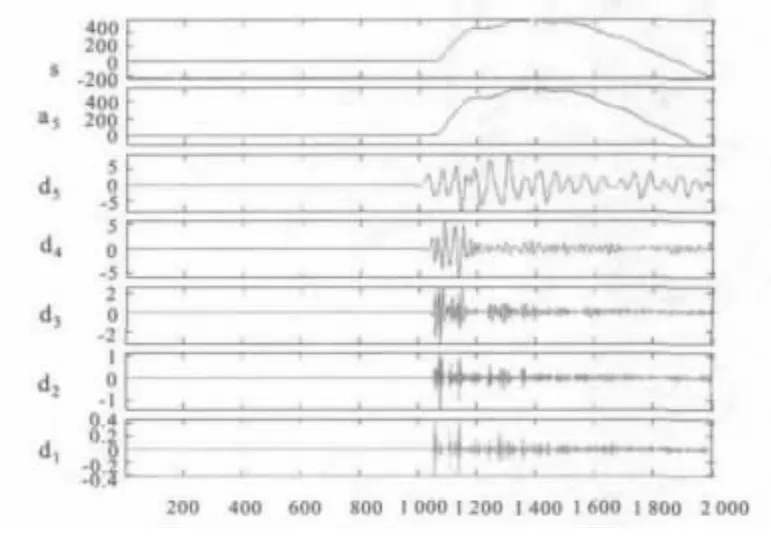
图5 电流行波的小波分量
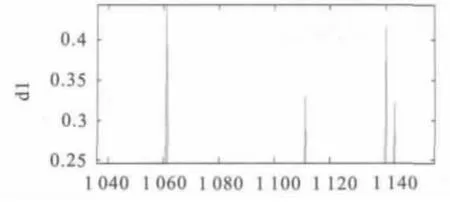
图6 电流行波的小波分量局部放大图
图5 中,采用db4 小波分析法进行行波波头的识别。初始行波到达故障点时间为1.061 ms,故障点反射波到达的时间差为1.111 ms。查找历史数据库,波速为2.98×108m/s。计算的故障测距的结果为74.5 km,误差为-500 m。显然,HHT 所计算结果的精度更高,对于故障定位而言更加可靠。当采样频率更高时,HHT 的精度可以进一步得到提升。表2 为在不同地点发生短路时,HHT 的定位结果以及与小波分析法的结果的比较。

表2 小波分析法和HHT 故障定位结果的对比 km
结果表明,HHT 方法应用于故障测距有效,并且可以达到高于小波分析法的精度,据此更好地验证了HHT 方法具有简单、高效、直观合理的优点。总而言之,Hilbert-Huang 变换完全根据信号本身在时域中自适应地分解,基函数在分解过程中自适应地随信号产生,不存在分解尺度和基函数的选取问题,可以得到精确的结果。而小波变换的基函数和分解尺度是预先确定的,不具有自适应性,对于信号的准确分析造成了影响。此外,HHT 方法具有良好的时频聚集性,它能根据不同的信号源精确地给出频率与时间的关系,不再如小波变换法受Heisenberg 测不准原理的制约,因此必然会提高故障测距的精度。HHT 正是从信号本身出发来进行分析,非常适合于非线性和非平稳性的信号。
6 结论
本文提出用Hilbert-Huang 方法进行故障测距:在对故障线路的行波进行EMD 分解后,进行了Hilbert 变换;采用第一阶IMF 分量计算故障距离。该方法不受行波波速误差和线路实际长度变化的影响,原理简单且方法容易实现,对高压输电线路故障位置的准确定位具有重要的价值。
[1]徐汝俊,张伟,熊高林,等.配电网故障测距方法的仿真分析[J].电力科学与工程,2010,26 (4):21-23.
[2]束洪春,王平才,司大军,等.小波变换应用于输电线路行波故障测距(I) [J].云南水利发电,2002,18(2):10-38.
[3]覃剑,陈祥训.基于小波变换技术的新型输电线路故障测距系统[J].电网技术,2001,5 (4):31-34.
[4]刘万超,陈平,孙佳佳,等.基于数学形态学的输电线路单端行波故障测距研究[J].电网与清洁能源,2009,25 (4):29-33.
[5]蔡秀雯,谭伟璞,杨以涵.基于数学形态学的配电网单端行波故障测距[J].现代电力,2006,23 (6):25-29.
[6]覃剑,黄振,邱宇峰,等.基于小波变换的同杆并架双回线双端行波故障测距[J].电力系统自动化,2004,28 (5):51-55.
[7]张正团,文锋,徐丙垠.基于小波分析的电缆故障测距[J].电力系统自动化,2003,27 (1):49-52.
[8]顾艳,王玉忠.基于小波变换和数学形态学的双回线故障测距[J].电力自动化设备,2011,31 (12):34-38.
[9]束洪春.电力工程信号处理应用[M].北京:科学出版社,2009.
[10]徐汝俊,严凤,裴玉龙.10 kV 配电网单相接地故障定位方法的研究[J].电力科学与工程,2010,26(11):14-17.
[11]施围,郭洁.电力系统过电压计算[M].北京:高等教育出版社,2006.
[12]胡婷,游大海,金明亮.输电线路故障测距研究现状及其发展[J].电网技术,2006,30 (8):146-150.

