基于EMD 聚类算法的配电网单相接地故障选线方法

廖桂源，李彩林，施 伟，孙新望

(桂林电子科技大学 机电工程学院，广西 桂林541004)

0 引言

随着配电网结构日趋复杂，谐振接地系统发生单相接地故障时故障信号不易检测和处理，致使现有的故障选线方法并不理想，需要对故障选线做进一步的研究［1～2］。

现有的谐振接地系统单相接地故障选线方法以故障暂态分量方法为主。文献［3］提出了在一定数据窗下将故障后各馈线零序暂态电流进行两两相关分析，由得到的综合相关系数序列确定选线的方法。但当配电网存在缆线混合线路时，各健全馈线和故障馈线的零序电流的相关性强弱有待商榷，单纯地以各馈线零序电流综合相关系数的大小确定故障线路可能造成误判［4］。文献［5］提出了通过对零序暂态信号进行小波变换并由变换系数确定故障馈线的选线方法;文献［6］提出了基于数学形态学的选线方法，通过数学形态滤波器对暂态信号进行滤波处理，利用形态学算子对滤波后的数据进行图变量检测确定故障馈线。但是小波变换和数学形态滤波存在抗干扰能力弱的缺点，经其处理的暂态信号可能失效进而影响选线结果。

EMD 是一种具有自适应的多分辨率分析方法，适合对非线性、非平稳信号进行分析［7］，因此对谐振接地系统发生单相接地故障后的故障暂态信号做EMD 分解可以有效、准确地获取信号特性。本文对谐振接地系统单相接地故障后各馈线的零序暂态信号进行EMD 分解，提取有效频带信号，并根据单相接地故障暂态特征求取有效信号的综合欧氏距离，以此进行排序和聚类，根据聚类结果确定故障馈线。仿真实验表明，该方法适应性强，选线结果正确。

1 单相接地故障暂态特征

谐振接地系统发生单相接地故障后，故障相对地电压降低，非故障相对地电压升高。因此可以将暂态电流看成故障相电压突然降低而引起的故障相放电电容电流和非故障相电压升高而引起的非故障相充电电容电流。因消弧线圈的补偿作用，发生单相接地故障时系统的稳态零序电流幅值很小，而零序电流的暂态分量幅值很大且具有下面的特点:健全馈线零序暂态电流大小与本线路对地电容的大小成正比且极性相同;故障馈线零序暂态电流等于所有健全馈线暂态零序电流之和，且电流极性相反［1］。

2 EMD 算法

EMD 算法即Hilbert-Huang 变换(HHT)，是由美籍华人Norden E．Huang 等人于1998 年提出的一种新的信号处理方法，是对傅里叶变换为基础的线性和稳态谱分析的一个重大突破。EMD 能根据信号的局部特征，自适应地将一个复杂信号分解为一系列本征模态函数IMF (Intrinic Mode-Function)和平均趋势项，比小波分析具有更好的适应性［7］。

EMD 分解算法将原信号I (t)分解为多个分量，每一分量即为本征模态函数IMF，分解结果由若干本征信号imfi(t)和一个残余信号rn(t)组成，即:

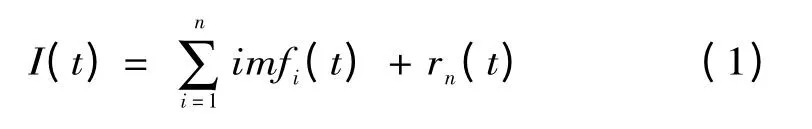
在整个信号序列上，每一个IMF 必须满足两个条件:极值点的个数和过零点的个数相差不大于1;信号上任意一点，由局部极大值点确定的包络线和局部极小值点确定的包络线的均值均为0，即信号关于时间轴局部对称。

EMD 算法是基于任何信号都是由若干有限的本征模态函数IMF 组成的假设，每一个本征函数可通过如下方法得到［7～8］。

(a)找出原信号I (t)的所有极大值点和极小值点，通过三次样条函数拟合得到原信号极大值包络线和极小值包络线并求取均值m1(t)，得

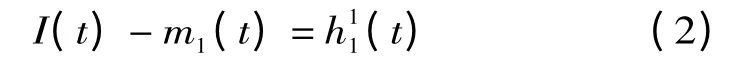
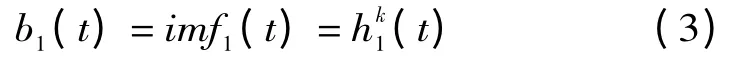
(b)将原信号I (t)减去b1(t)得到一个去掉高频成分的信号r1(t)，即

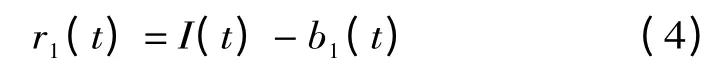
(c)对余量r1(t)重复(a)，)b)步骤得到第二个IMF 分量b2(t)。

反复上述(a)，(b)，(c)步骤，一直到第n 阶IMF 分量bn(t)的剩余分量rn(t)小于预设阈值;或当rn(t)是单调函数或常量时，EMD分解过程停止。最后I (t)经EMD 分解后得到

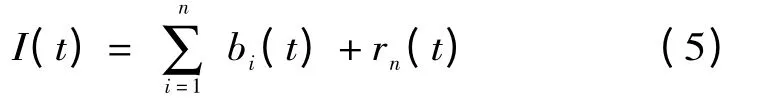
式中:rn(t)为趋势项，代表信号的平均趋势或均值。

3 欧氏距离与聚类算法

欧氏距离 (Euclidean distance)是计算各个数据对象相异度最常用的距离度量，以此为基础可以对数据进行聚类分析。设i = (i1，i2…，in)和j= (j1，j2，…，jn)为两个n 维的数据对象，则它们间的欧氏距离定义为:

则d 的大小表征两个数据在数值差上累积的结果。以欧氏距离为基础的聚类算法是数据统计研究中“物以类聚”的一种理论:通过一定的准则将物理量或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程，使相似的数据样本归为一类，便于分析处理。聚类算法最常见的是系统聚类，其聚类过程如下［9-10］:

(a)计算数据样本两两之间的欧氏距离。

(b)视每一数据样本为一类，合并距离最近的两类为一新类。

(c)计算新类与当前各类的距离，判别类的个数是否等于1，不为1 则转向步骤(b)。

(d)类的个数如果为1，结束迭代计算，决定分类的个数和类别。

4 故障选线原理及仿真分析

4.1 故障选线原理及选线流程

设配电网有k 条馈线L1，L2…，Lk。发生单相接地故障后，各馈线零序暂态电流为Il1，Il2…，Ilk。谐振接地系统单相接地故障后的零序暂态特征:故障馈线零序暂态电流幅值是各健全馈线暂态零序电流幅值之和，且电流极性相反;各健全馈线暂态零序电流电流幅值大小与本线路对地电容成正比，且电流极性相同。根据欧氏距离定义可知，故障馈线的零序暂态电流与其它健全馈线的零序暂态电流的欧氏距离最大而与健全馈线之间零序暂态电流的欧氏距离较小。因此，以欧氏距离为基础的聚类算法可将k 条馈线分为两大类:唯一的故障馈线和剩余的健全馈线;若所有馈线聚为一类则为母线故障。选线流程为:

(1)利用EMD 算法对谐振接地系统单相接地故障后各馈线零序暂态电流Il1，Il2…，Ilk进行分解，并把剩余趋势项r1n(t)…rkn(t)作为各馈线有效频带数据［8］。

(2)对各馈线暂态零序电流有效频带数据r1n(t)…rn(t)利用式(6)求取两两间的欧氏距离得到欧氏距离矩阵

用矩阵元素dij表示第i 条馈线和第j 条馈线的零序暂态电流的欧氏距离，则欧氏距离矩阵N 为主对角线元素为0 的对称矩阵，根据N 求取馈线Lk相对于其他线路的综合欧氏距离:

(3)根据dk对各馈线暂态零序电流的综合欧氏距离进行排序。综合欧氏距离越大表征该馈线是故障馈线的可能性越大。以综合欧氏距离为基础，利用上文所述的系统聚类算法步骤对各馈线进行聚类。为保证聚类结果的精度与裕度，设在同一类别中，最大综合欧氏距离为dmax，最小综合欧氏距离为dmin，则聚类结束的阈值设置值m≤0.2，且m 由下式确定:

根据聚类算法对各馈线进行聚类。若聚类结果将各馈线分为两类，且其中一类有唯一的馈线，则此馈线即为故障线路;若聚类结果将各馈线分为一类则判定发生母线故障。

4.2 仿真分析与验证

为验证选线方法的可行性和准确性，采用Matlab 电力系统模块搭建谐振接地系统单相接地故障仿真模型。系统采用5 条10 kV 馈线，其模型如图1 所示:其中线路1、3 为架空线路，2、4为电缆线路，线路5 为缆线混合线路，消弧线圈补偿度取为过补偿7%。

图1 单相接地故障仿真电路模型

设置馈线L5的A 相在0.02 s，20 km 处发生接地故障，接地电阻为10 Ω，故障电压起始角为0 度。因篇幅的原因，在此仅选取其中馈线L4、馈线L5经EMD 算法处理后的暂态零序电流，如图2 所示。根据选线流程求取各馈线L1，L2，L3，L4，L5的零序暂态电流的综合欧氏距离为:［64.4，65.6，61.6，61.7，184.4］。以此为基础进行综合欧氏距离排序，则L5 是故障馈线的可能性最大;利用聚类算法对各馈线进行聚类可将馈线L1，L2，L3，L4聚为一类，L5为单独类。据此确定L5为故障馈线，与试验预设一致。

为检测选线方法的效果，仿真试验预设系统在不同故障点、接地电阻、初始电压故障角时发生单相接地故障并进行了验证，其结果如表1所示。

从表1 可以看出，选线方法对于故障接地电阻、故障电压起始角和故障位置不同的情形都有准确的选线效果。非母线故障时，故障馈线为综合欧氏距离最大者，而母线故障时各馈线间的综合欧氏距离相差较小;但最终选线结果由聚类算法的分类决定。如表中预设情形:故障接地电阻10Ω，故障电压起始角为0 度，母线故障时，最大综合欧氏距离为馈线L1;但由聚类算法得到的结果是各馈线分为一类，故判定是母线故障，而不是综合欧氏距离最大的馈线L1。

图2 EMD 分解后馈线L4，L5 暂态零序电流

表1 实验结果

5 结论

本文提出了一种基于EMD 算法和聚类算法相结合的谐振接地系统单相接地故障选线方法。对于单相接地故障信号不易测度和处理，影响选线判据有效性的情形，利用EMD 算法对故障暂态零序电流进行分解并提取有效频带数据，根据单相接地故障时故障馈线与健全馈线零序暂态量在幅值和极性上的差异，求取各馈线零序暂态电流经EMD 分解的有效频带数据的综合欧氏距离，利用聚类算法对各馈线进行聚类确定故障馈线。在复杂配电网出线馈线增多的情形下，故障馈线和健全馈线间暂态零序电流间的综合欧氏距离差异更为明显，选线方法会有更好的选线精度。仿真实验表明，在不同的故障情形下该选线方法准确、可靠。

［1］束洪春．配电网络故障选线［M］．北京:机械工业出版社，2008．

［2］郭清滔，吴田．小电流接地系统故障选线方法综述［J］．电力系统保护与控制，2010，38 (2):146-152．

［3］毛鹏，段玉倩，姜娜．基于相关分析的故障选线方法［J］．电网技术，2004，28 (2):36-39．

［4］王韶，朱姜峰．基于改进相关性分析法的配电网络单相接地故障选线［J］．电力系统保护与控制，2012，40(15):76-81．

［5］吴谢东．基于小波变换的配电网故障选线的研究［J］．电力科学与工程，2006，(2):21-24．

［6］任建文，孙文武，周明，等．基于数学形态学的配电网单相接地故障暂态选线算法［J］．电力系统自动化，2008，32 (1):70-74．

［7］Huang N E，Shen Z，Long S R，et al．The empirical mode decom position and the Hilbertspectrum for nonlinear and nonstationary time series analysis ［J］Proceedings of the Rogal Society of London，1998，454:(1971):963-995．

［8］张宇辉，汪利君，兰华，等．基于EMD-相关性算法的谐振接地系统故障选线新方法［J］．电测与仪表，2012，49 (564):7-11．

［9］张尧庭，方开泰．多元统计分析引论［M］．北京:科学出版社，2003．

［10］徐岩，刘金生，张亚刚，等．聚类算法在电网故障元件定位应用中的研究［J］．电力系统保护与控制，2010，38 (12):13-18．