基于模糊数学的湘中凹陷圈闭评价
朱 伟,米茂生,曹子剑
(1.湖南科技大学,湖南 湘潭 411201;2.湖南省地质矿产勘查开发局,湖南 长沙 410014)
引 言
湘中拗陷位于雪峰古陆以南,华南褶皱系的北部,是一个以下古生界浅变质岩系为基底发展起来的晚古生代沉积坳陷区。该区元古界—中生界地层均有出露,且主要分布在坳陷的涟源、邵阳、零陵3个凹陷中[1]。湘中涟源凹陷位于湘中拗陷北端,位于新化—双峰一带,整体呈北西西向展布,出露地层主要为泥盆系—三叠系,区域构造线呈NE—NNE向。在稳定的沉降历史过程中,发育了5 000余米厚的碳酸盐岩夹碎屑岩,同时以测水组煤系地层作为区域性盖层为该地区油气藏的形成提供了良好的生储盖组合。但自古生代以来分别经历了印支运动、燕山运动、喜山运动等大的构造运动阶段,使得油气成藏条件复杂,不确定性因素较多。
模糊数学是引用隶属函数的概念建立的数学体系,隶属函数可以用[0,1]区间内的任意值来描述一个对象是否属于该集合[2],把绝对的属于或不属于拓展为具有描述事物渐变过渡的能力。由于模糊数学具有不确定性,同时还能确定事件的发生与否,在面对复杂地质情况时具有综合评判优势[3-4]。在湘中油气勘探中运用模糊数学方法可以更客观评价油气藏[5-7]。
1 储层物性研究
该区可划分为西部叠瓦逆掩冲断带、中部隔挡式褶皱带、东部滑覆断皱带[8]。据现有资料分析,涟源凹陷下石炭统(C1y1—C1d1)储层岩石类型以灰岩为主,局部发育砂岩储层。从192块井下样品测试分析结果看,绝大多数样品的孔隙度小于1.5%,渗透率一般小于0.1×10-3μm2,属低孔、低渗储层。在这些样品中,仅有9块样品达到了有效储层的孔隙度下限值(2%),占样品总数的4.7%,表明该区的储层发育程度差。造成该区储层不发育和储层物性差的主要原因是,晚期成岩作用(压实、胶结、重结晶等)使岩石中的原生孔隙基本上被破坏,有效储集空间主要为次生溶孔、白云化晶间孔及构造裂缝。湘中地区发育有两大类储层,即碳酸盐岩和碎屑岩储层。其中碳酸盐岩包括生物礁、粒屑滩和白云岩3类。主要发育于台坡相(如下石炭统坪烟背斜、桥头河背斜、安坪背斜、杨1号隐伏背斜、杨3号隐伏背斜、石山冲背斜)和台滩相(如禁田断鼻、满竹背斜、娄底背斜)。
2 圈闭保存条件
该区测水段的含煤地层可作为目的层(C1y1—C1d1)的区域盖层。测水煤系本身具有很强的生烃能力,能很好地抑制下伏目的层的天然气扩散。测水煤系的致密泥岩及煤岩不仅可以作为天然气的岩性封盖层,也可以作为天然气的烃浓度盖层;以下石炭统孟公拗组(C1y2)、刘家塘组(C1y3)和石磴子组(C1d1)为主力烃源岩层,刘家塘组(C1y3)和石磴子组(C1d1)碳酸盐为储层,构成垂向上的生、储盖组合。分析认为,大幅度抬升剥蚀及近地表渗漏是造成该区天然气大量散失的主要原因。
据区域地质资料分析,印支期后期也就是生油高峰后,为该区主要抬升期。抬升剥蚀幅度大都超过3 000 m。禁田逆断层以西为西北断褶带,构造变形以逆冲断裂和线性褶皱为主,造成区域盖层严重破坏,导致一部分目的层(C1y1—C1d1)直接裸露地表,加速了天然气的渗漏或逸散的速度,加上该区烃源条件较差,导致天然气难以聚集。禁田逆断层以东至麻阳洞逆断层以西的地区为变形相对较弱的中部褶皱带,由一系列宽向斜与窄背斜组成“隔档式”构造样式,宽向斜内二叠系保存较完整且大面积分布,有利于下石炭统天然气的保存。加上该区地处涟源凹陷主力气源区,烃源条件较好,气显示丰富,为较有利天然气聚集区。麻阳洞断层以东为东部断褶带,其保存条件介于西北部褶皱带和中部褶皱带之间。因此西部断褶带保存条件差,中部褶断带较好,东部断块带保存条件较差。
3 模糊数学圈闭评价
根据模糊数学原理可以建立综合评级模型[9-13]。
(1)设模糊集U为待评价因素的子集合:U={Ui},i=1,2,……,n。
(2)设论域V为评价级模糊子集合:V={Vj},j=1,2,……,m。
模糊集合是用隶属函数来描述的,首先确定因素集合,再来确定每个因素属于论域E的隶属度。隶属函数有模糊统计法、例证法、专家经验法、二元对比排序法。
根据每个因素的重要性,依据专家打分法,确定每个因素的权重 A=W·E=(a1,a2,…,am),进行模糊综合评价运算得公式(1):

式中:aj为第j个评价值;wi为第i个权重值。
第一,同行竞争加剧。2017年共享单车在全国各地打响正面竞争,激烈竞争带来高推广成本。每当一家公司开通一座城市时,就会有少则数万辆多则数十万辆的单车投入。同时要跟进单车转运团队,单车运营团队和当地运营推广团队,再加上单车的成本费用和线上线下的推广运营的费用,使部分企业无额外的资金回收维修废料共享单车。第二,用户忠诚度难培养。共享单车是工具类产品,依靠用户。在赢取用户信任前,大部分用户会进行产品体验,互相借鉴。部分企业难以保证能赢得用户的青睐。第三,部分企业管理能力有限。部分企业缺少相关的专门管理机制,内部维修人员有限,维修人员维修能力不强。
3.1 模糊数学评价步骤
研究区内沉积相主要为台盆、三角洲、潮坪相,储层主要发育于下石炭统测水组、刘家塘组及石磴子组,构造条件复杂,圈闭类型多样,故将其评价工作分如下几步进行。
(1)设定地质要素评价体系。根据成藏过程中形成圈闭各要素的不同影响程度,分别赋予权值W。湘中盆地的圈闭评价体系可由静态因素(构造、储层、盖层及封闭条件)及动态因素(时空匹配关系、油的聚集及保存条件)构成。
(2)确定地质各要素隶属度。根据专家评价法将最有利的定为1,最差的定为0,做出相应隶属函数,之后将有关数据代入获得相关地质要素的隶属度。
(3)模糊数学的综合评价。通过一级、二级的模糊预算,得出综合评价结果,确定有利圈闭。
3.2 地质因素评价标准
湘中盆地涟源凹陷的油气藏主要受构造、岩性、油源条件及保存条件影响。因此,在综合评价时,对主控因素分配较大权值,对其他控制因素分配相对较小的权值。
在评价圈闭含油气时,采用的地质条件因素一般为(包含权重):①构造条件(0.30),在构造条件中圈闭类型给出的二级权值为0.40,圈闭面积为0.60;②油源条件(0.15),其中烃源岩厚度、有机碳含量、有机质类型、有机质成熟度分配的二级权值分别为 0.35、0.30、0.30、0.05;③ 盖层条件(0.30);④保存条件(0.25)。
3.3 评价计算
该文主要采用专家打分法和逻辑函数法来确定其隶属度,涟源凹陷成油气地质条件评分标准见表1~4。
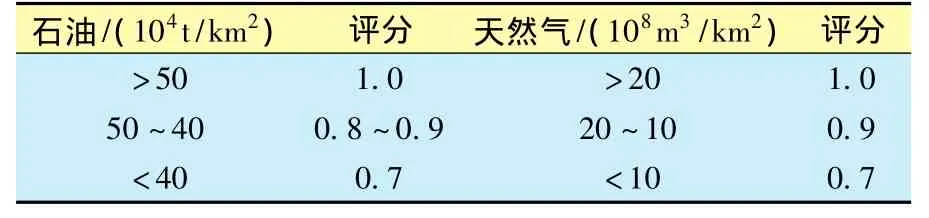
表1 涟源凹陷成油气烃源条件评分标准

表2 涟源凹陷成油气储集条件评分标准
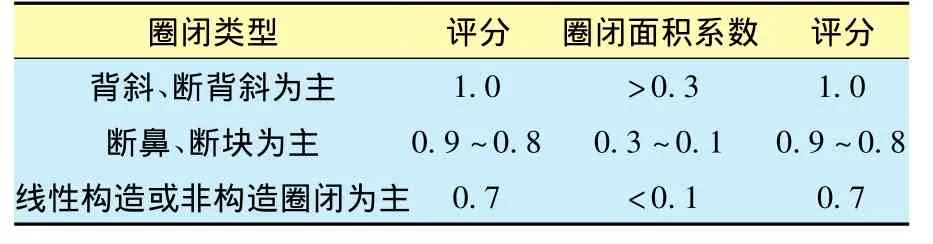
表3 涟源凹陷成油气圈闭条件评分标准

表4 涟源凹陷成油气保存条件评分标准
根据盆地各区带勘探程度不同,采用定量和半定量方法,如通过指标值与该区域内该指标最大值的比值来评价其隶属度。
通过计算圈闭面积隶属函数分析圈闭的类型,确定圈闭的优劣度:
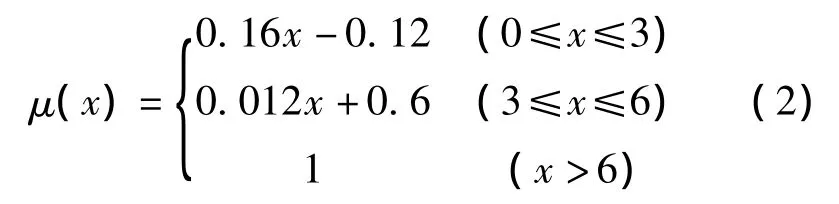
式中:x为圈闭面积,m2。
区内圈闭条件因素见表5。

表5 涟源凹陷圈闭条件
3.3.2 生油岩条件
从以下几个方面进行分析。
(1)对于石炭统的生油岩厚度评价,采用隶属度函数:

式中:m为最大烃源岩厚度,m;α为研究区平均烃源岩厚度,m。
(2)有机碳平均含量隶属函数:

式中:β为有机碳平均含量,%。
(3)生油岩有机质类型隶属函数:

式中:ki为生烃潜力系数,其中Ⅰ型为1.00,Ⅱ型为0.60,Ⅲ型为0.25;γi为某种类型的有机质所占的比例,%。
(4)生油岩的成熟度(专家打分法),以Ro为评价标准,不同学者划分的数值稍有不同,但大致相当。本文采用划分为未成熟阶段、成熟阶段、过成熟阶段方案[14]。由于该区的 Ro≥2,属于过成熟阶段,是主要的生气阶段,因此生气条件好(表6)。

表6 涟源凹陷生油有机质综合表
3.3.3 综合条件评价
对圈闭及生油岩分别进行一级运算。
(1)圈闭。

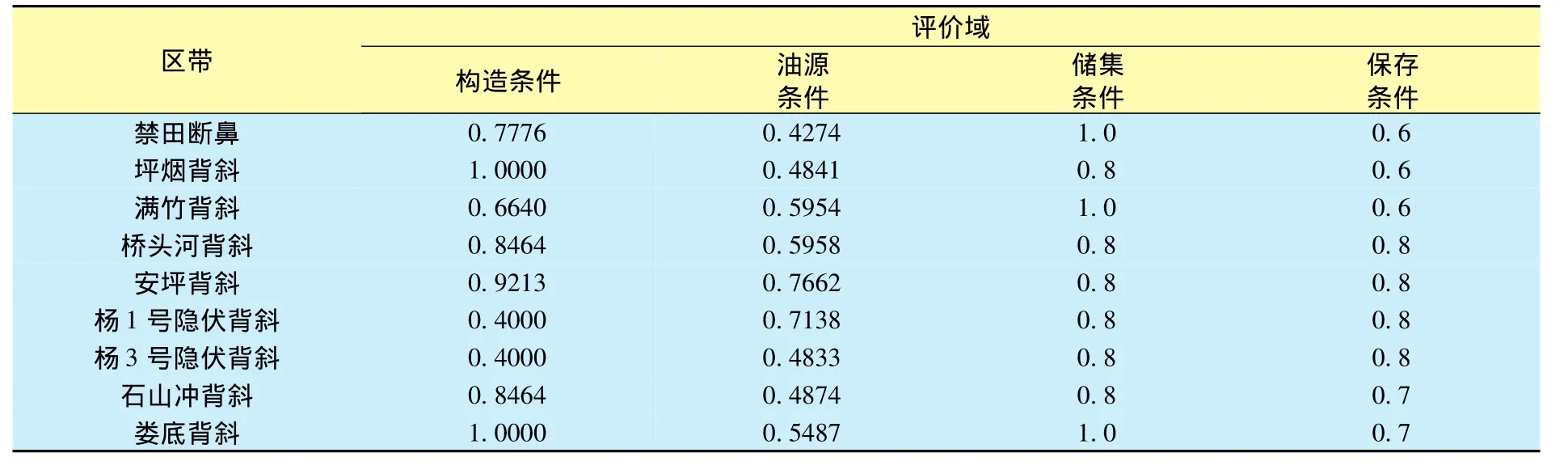
表7 涟源凹陷部分局部构造有关数据
结合模糊数学的综合运算,得出的综合评价如表8所示。
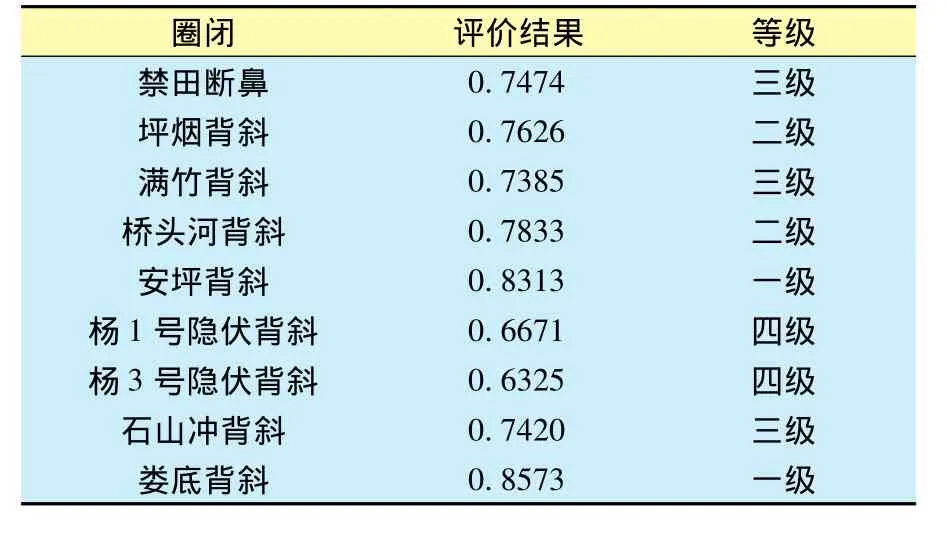
表8 模糊数学综合评价
由计算结果可知,该区地质条件十分复杂,影响油气分布,影响预测工作的准确性。借助于模糊数学,最终可以推断涟源凹陷的娄底背斜、安坪背斜的石炭统油气成藏条件较好,是生气的优势圈闭。应用该方法,可优化勘探决策,提高油气勘探的效果,为以后取得勘探突破奠定基础。
4 结论
(1)湘中涟源凹陷构造条件好、生气条件较好,储层物性一般,并经历多期次构造活动,成藏地质条件复杂,存在诸多不确定性影响因素,传统评价方法在评价过程中难免存在主观性。
(2)运用模糊数学方法,经过计算分析选出湘中涟源凹陷娄底背斜、安坪背斜为成藏条件较好的圈闭,同时与实际勘探效果较为吻合,可作为一种有效评价手段,为今后的勘探工作提供依据。
[1]王建,李三忠,金宠,等.湘中地区穹盆构造:褶皱叠加期次和成因[J].大地构造与成矿学,2010,4(2):159-165.
[2]刘为付,孙立新,刘双龙,等.模糊数学识别火山岩岩性[J]. 特种油气藏,2002,9(1):14-17.
[3]朱伟,顾韶秋,曹子剑,等.基于模糊数学的滨里海盆地东南油气储层评价[J].石油与天然气地质,2013,34(3):357-362.
[4]杨柏,杨少春,姜海波,等.胜坨油田储层非均质性及与剩余油分布的关系[J].特种油气藏,2009,16(4):67-70.
[5]Finol J J,Guo Y K,Jing X D.Fuzzy partitioning systems for electrofacies classification[J].Petroleum Geology,2001,24(4):441-458.
[6]唐庆宝.应用模糊数学方法评价局部圈闭[J].石油地球物理勘探,1985,20(5):490-495.
[7]伊广林.在储集层油气评价中模糊数学的应用[J].测井技术,1982,6(4):20-29.
[8]朱伟,易积正.湘中涟源地区复杂地质结构与天然气勘探潜力[J]. 特种油气藏,2012,19(3):35-38.
[9]王翠香.模糊集合的模糊度的一种表示形式[J].数学的实践与认识,2006,36(2):267-269.
[10]杨凯.模糊数学在矿山环境影响评价中的应用[J].四川环境,2010,29(3):127-130.
[11]李鸿吉.模糊数学基础及实用算法[M].北京:科学出版社,2005:52-53.
[12]Dave N R.Fuzzy shell-clustering and applications to circle detection in digital images[J].Int J.General Systems,1990,16(4):343-355.
[13]Dubois D,Prade H.Fuzzy sets and systems theory and application[M].New York:Academic Press,1978:81.
[14]黄第藩,李晋超,等.陆相有机质的演化和成烃机理[M].北京:石油工业出版社,1984:74-76.

