税收优惠政策对高新技术企业生产率的影响
李延晨
(山东 大学商学院金融学系,山东 威海 264209)
税收优惠政策对高新技术企业生产率的影响
李延晨
(山东 大学商学院金融学系,山东 威海 264209)
本文对我国北方某市45家高新技术企业的面板数据进行短面板回归,并针对不同规模企业分析研究了高新技术企业所得税优惠政策和技术开发费用加计扣除政策对企业生产率的影响。在此基础上,运用pvar模型,分析企业所得税优惠政策五年来对企业生产率冲击的演变过程。
高新技术企业;税优惠政策;生产率
一、文献回顾
伴随着旧有经济发展模式渐渐同现下国情脱节,我国经济增长速度放缓。政府的财政政策将成为时下经济革新的有力工具。税收对经济发展波动的冲击从95年以来逐渐增强,成为决定我国经济平稳增长的关键(吕光明,2012)。同时,罗默(2000)指出经济增长的长期影响因素要在一定结构下才能高效发挥作用。因而在研究税收对经济作用时,常常涉及到经济结构。曹海娟(2012)、安体富(2011)等中国学者分析了我国全国层面上产业结构现状和税收政策的关系,其中曹海娟(2012)利用pvar法详细实证了税收结构在我国东、西、中部对产业结构具有不同效果的冲击。税收结构确实很好地发挥了积极作用,但在东部地区表现得并不显著,且效果起伏较大。地区间的差异表明,对统一的宏观数据进行分析可能会带来偏差,并影响研究结果的指导意义。将研究视角从全国整体层面,向地区层面转变具有必要性。
税制对区域经济影响遵循“税收→价格→企业→产业→区域经济”的路线(闫伟,2005)。税收对区域内某部分企业的影响最终会渐渐扩散到区域内的产业结构。同时,冯瑜(2011)指出产业内部存在明显的失衡:工业内部存在大量依靠资源发展的落后企业、大部分农村地区农业生产技术落后、高新技术产业创新不足等。从微观入手分析税收政策对企业的影响,不仅能够从一个层面反映出地区产业结构的变化,还能深入探讨产业结构内部的不合理现象。本文试图对地区产业结构中的高新技术企业这一微观层面进行实证分析,从而得出更加准确的结论。
杜军和王皓妍(2013)对江苏常州市高新技术企业进行了实证分析,发现高新技术企业技术开发费用加计扣除(inv)政策、所得税优惠(rat)政策对企业盈利能力有明显促进作用,使得高新技术企业得以不断发展。上述文献是以技术投入和盈利作为衡量高新技术企业发展的指标。李平、李淑云、许家云在研究高新技术企业技术创新时,则以专利数作为考察指标。这些指标都能反映出地区技术的进步,但技术进步的动力来源最终是各高新技术企业。这些企业所作出的各种技术创新最终是为了提高劳动生产率,这也是高新技术企业长期发展的关键。本文利用ces生产函数模型来构建衡量劳动生产率的模型。本文借鉴王良举、陈甬军(2013)的做法,将影响企业技术水平的因素分为企业异质性因素和制度环境因素。这样做是因为技术水平是影响劳动生产率的重要因素,并且是rat、inv对劳动生产率施加影响的主要途径。其中异质性因素主要考虑企业规模,制度环境考虑rat、inv。并进一步深入,分别估计大、小规模企业模型,分析上述政策的作用。本文采用2009-2013年北方某市45家符合条件的高新技术企业数据,通过引入伍德里奇构造的辅助方程,使用随机效应模型的方法用stata进行短面板分析,试图实证rat、inv的影响。同时为了能够从五年整体出发,了解各年政府政策的有效性,本文还运用pvar模型验证高新技术企业所得税优惠政策对企业劳动生产率的冲击。选择rat,主要因为相对于inv,rat更具有稳定性,适合进行面板数据的时间序列分析,能获得更加可靠的结果。
二、数据与模型
(一)数据说明
本文收集的数据为2009-2013年间,45家享受所得税优惠政策企业的财务信息。税收政策随着时间的推移,在实际操作中得以不断推广、完善,享受税收优惠政策企业数量逐年增加,而且由于企业自身发展的影响,同一企业也可能在某些年份无法享受政策优惠。因而选取了所有样本中2009-2013年五年间数据较为齐全的45家企业为研究对象。对个别遗漏的企业财务、生产数据运用插值模型进行补全。目前每年获得高新技术企业资格且享受所得税优惠政策的企业数逐年增加(见图1),但近五年来,能够稳定获得政策支持的企业并不多,其中五年能连续获得rat资格的企业只为27家。为了简化估计过程,本文所用的数据中,企业所得税、rat、inv、企业营业收入、企业管理费用和营业费用、企业固定资本、企业职工工资这些数据单位都是万元。
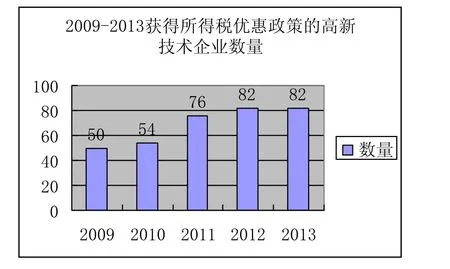
图1
(二)模型设定
本文采用ces生产函数模型作为基本模型,引入关于企业的税收政策来进行实证分析。基本假设为企业的生产规模报酬不变,且企业会选择生产函数上资本和劳动的边际产量等与这两种生产要素边际成本的最佳点从事生产活动。基本模型:
Yit=A[δKit-ρ+(1-δ)Lit-ρ]-1/ρ(1)
其中Yit为企业的营业收入,Kit为企业固定资本量,Lit为职工人数,下标i表示企业,t表示时间。本文采用企业营业收入除以职工人数作为生产率的度量指标,得到企业的劳动生产率LPit:
yit=Aδ-1/ρ[kit-ρ+(1-δ)/δ]-1/ρ(2)
其中yit表示人均产出,kit表示人均固定资本存量。
由于企业会根据生产函数和投入约束线来确定自己的最佳生产点。所以:mpl/mpk=w/r,对(1)式进行求导便可得出mpl、mpk,其中ω为工资率,r为一年期贷款利率。mpl、mpk为劳动、资本的边际产量。将其带入(1)式得:
(1-δ)/δ*kitρ+1=ω/r(3)
将(3)式代入(2)得:
yit=Aδ-1/ρ[kit-ρ(ω/r*Lit/Kit+1)]-1/ρ(4)
在这里我们可以将ω*Lit和r*Kit当作企业在劳动及资本上所付出的成本,可以视为前定变量。对等式两边求对数可得:
lnyit=lnA-(1/ρ)lnδ+lnkit-(1/ρ)ln(ω/r*Lit/Kit+ 1)(5)
其中lnδ可视为常数。
生产函数中的技术进步是一个综合指标,不仅包含科学技术或工艺水平,还包括管理水平、劳动者能力、产品结构等因素。除此外,制度环境对企业生产率有重要影响,王良举和陈甬军(2013)在影响企业技术因子的模型构建中引入以市场化进程变量作为制度环境的代理变量,并且建立了一套表现企业异质性的指标体系以完善模型[1]。本文则从rat、inv对企业生产率影响出发,选择rat、inv作为制度环境的代理变量。同时将企业规模和与企业日常生产管理、员工培训、技术投入活动有密切关系的管理费用、营业费用结合起来,综合衡量不同企业的性质。建立模型:
lnA=λXit+φGit+εit(6)
其中Xit表示异质性变量,Git是制度环境控制变量,εit为随机扰动项。Xit包含scale、c两项,其中scale是表示规模的虚拟变量,c表示企业管理费用和营业费用的加和。Git包含两项:rat*t、inv*t。由于rat和Inv都是企业所得税(t)的减免措施,是通过影响所得税来作用于企业生产的,因而这里引入rat、inv与所得税(t)的交互项来反映这一点。lnwk代表ln(ω/r*Lit/Kit+1)最后将(6)式带入(5)式可以得到最后的模型:
lnyit=λXit+φGit-(1/ρ)lnδ+lnkit-(1/ρ)ln(ω/r*Lit/ Kit+1)+εit
三、实证结果和分析
本文采用的数据为平衡的短面板数据,整个估计过程使用软件stata12。使用wooldridge建立的辅助方程在消除模型可能具有的异方差后,检验模型究竟是用随机效应模型,还是固定效应模型。结果ρ=0.0035,即能拒绝原假设“γ=0”,所以可采用固定效应模型进行回归估计。再根据stata输出结果中的F检验,可以得知固定效应模型比混合模型更为合适。
最后得出计量结果:
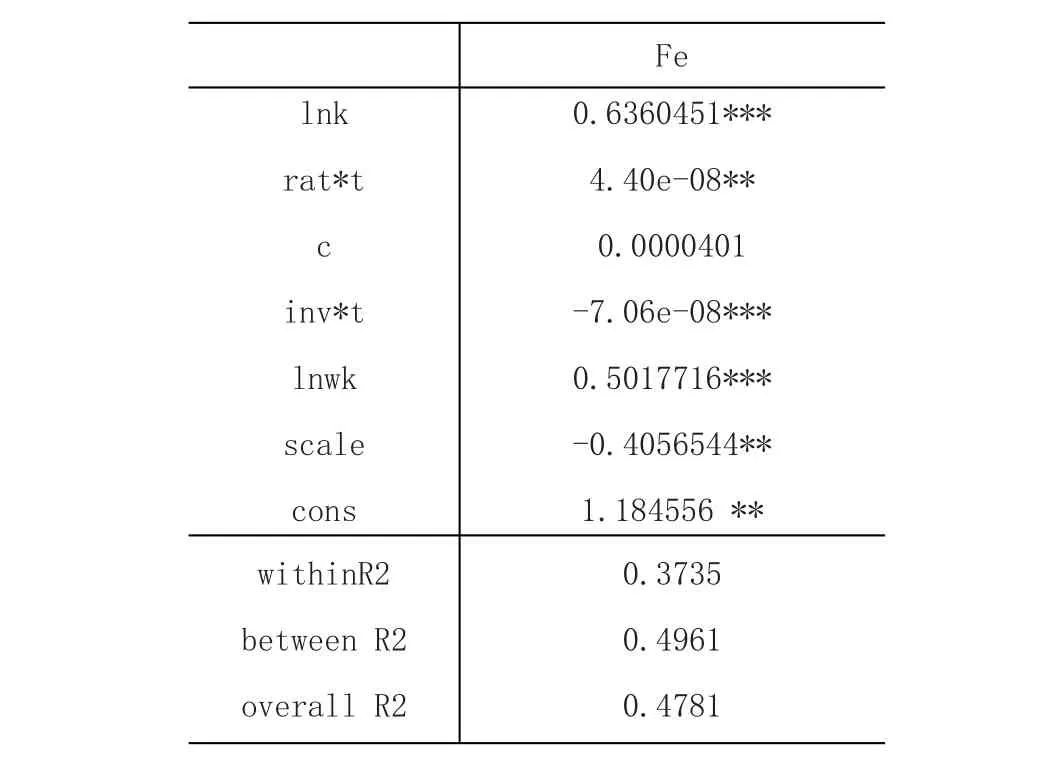
表1
(一)对不同规模企业的区分研究
对上述数据再次进行回归估计,这次将企业分为大、小规模两类。其划分标准按照国家统计局分类方法,把企业员工数大于300的划分为大规模企业,小于300的则划为小规模企业。回归结果见表2:
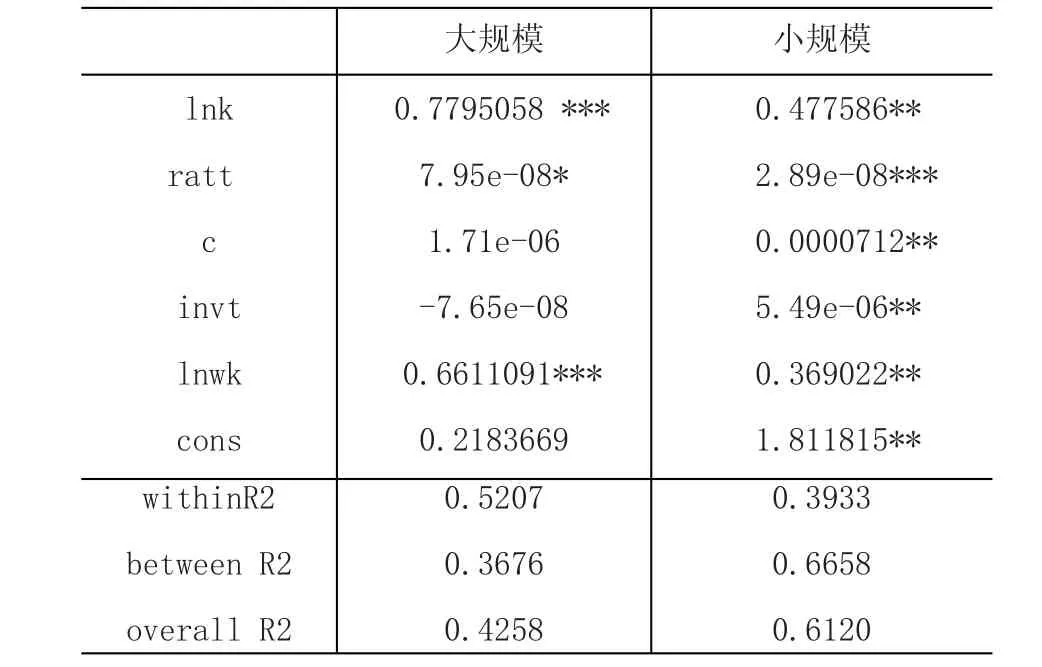
表2
针对大企业而言,rat对企业生产率的影响明显比小企业更为显著,这表明rat政策在企业规模更大时对企业发展更具影响力。从上述结果可以清晰看出,大规模企业劳动生产率的提高对人均资本存量有较大依赖性。在现阶段大规模高新技术企业人力11000222资本相对于固定资本有所富余,不断积累人均资本存量,充分发挥已有人员的潜能十分重要。Rat则可以为企业提供一笔数额较大的资金用于资本积累。但inv对企业的影响呈现反相关系且与企业生产率的关系非常不显著,一是与inv政策执行中存在起伏大的特点有关,二是大规模企业相对更需要提高非高新技术设备的引进,改善与生产相关的配套设施[2]。对于小企业而言,inv、rat则都十分重要,反映出小企业更依赖企业内部的资金流,其中inv对小企业有突出影响,折射出相对于大企业而言,小企业更需要关于引入高新技术设备的政策支持,以弥补其规模上的劣势。
从营业费用和管理费用上看,小企业在日常支出上存在很大的改进空间,加大各项支出对企业发展的作用明显。小企业良好的内部结构,使得各项支出可以得到充分利用,诸多企业自主管理的费用支出可以不断完善企业内部管理,提升员工素质,优化产品的销售流程等。大企业在这方面则相反,内部结构的冗杂可能带来资金使用率的低下,并且诸如:车船使用税、房产税、印花税等税金的支出也加重了企业的负担。
(二)利用pvar模型分析五年来政策的效果
为了能够研究高新技术企业所得税优惠政策五年来同企业生产率相互作用关系的演变,本文针对上述两个变量的对数形式构建了pvar模型。
Pvar模型的优点在于可以有效估计时间跨度短但截面数据丰富的数据,即降低了var模型对时间长度的要求,又可以捕捉到个体的微观行为。[3]本文运用love和zicchino(2006)编写的程序进行pvar模型的回归估计并画出脉冲响应图。为了能保证上述变量的稳健性,本文综合使用现在较为常用的面板数据单位根检验方法。原假设为“序列存在单位根”,结果为表3:
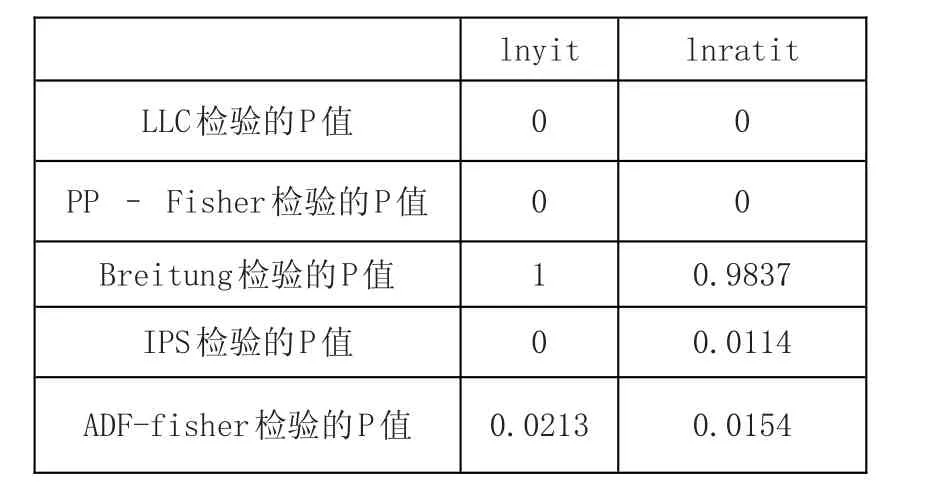
表3
由上述结果可知对于lnyit lnratit在除breitung法外的其他方法检验下的结果均显示出序列不具有单位根,可以认为这两个序列是平稳的。
针对研究对象建立模型:
zit=αi+ηt+β0+pi=1∑βizi,t-p+εit
其中αi为个体效应,ηt为时间效应,zit为两个变量的列向量(lnyit lnratit),i代表样本个体,t代表时间,p代表滞后项,εit为“白噪声”扰动项。由于整个回归过程是为了分析劳动生产率和所得税优惠政策两个变量间关系,为了减少其他变量的影响,在进行回归前,先使用组内均值差分法来消去模型中的时间效应,再对模型采用前向均值差分法来去除个体效应αi以避免其与自变量间可能存在的相关性。由于现在税收优惠政策刚实行5年,现阶段企业劳动生产率的提高更依赖于非政策因素,并且如上文分析,现在各项政策实行过程中稳定性不强,企业各项数据往往在短期内保持相对稳定,因而本文假设目前的技术开发费用加计扣除和高新技术企业所得税优惠政策对企业具有短期而非长期的影响,前一期所减免的所得税会对现期企业行为产生一定滞后影响。通过对模型进行混合回归也发现,各滞后一期的内生变量系数明显较为显著,所以在这里滞后项选取为1[4]。然后运用蒙特卡洛模拟法,进行1000次模拟回归得出方差的分解结果。
四、结论与启示
本文研究结果表明,现阶段两项税收优惠政策都具有一定的促进作用,但对于大、小规模企业而言,其影响则有明显的差异;企业在保持人均资本存量的同时,应努力提高企业职工个人工资率。启示如下:
第一,高新技术企业所得税优惠政策和技术开发费用加计扣除政策整体上对高新技术企业生产率的提高影响效果并不明显,必须针对不同规模企业制定拘束条件和优惠力度不同的政策细则。对于大规模企业,应该相对放宽高新技术企业所得税优惠政策的执行范围,同时加大优惠力度;对于小规模企业,则应提高技术开发费用加计扣除政策上的优惠力度,并针对该项政策执行不具有连续性、稳定性的问题进行改进。
第二,为了不断改进企业的生产率,必须将一定量的资金投向企业各项运营支出中,以改善企业对人员及各类物资的管理、使用。现在关于高新技术企业的优惠政策往往以企业的高新技术产品(服务)的产出为核心,只关注企业专利、技术应用的过程,而忽视对企业其他支出的支持。针对企业同外部相联系且不具有完全自主权的支出,政府可以代替企业加大投入。
第三,引入pvar模型可以从时间序列上整体观测rat对劳动生产率的冲击,分析现实中rat政策的连续性。现在高新技术企业所得税优惠政策对企业劳动生产率的影响并不显著,且实施五年来的效果变化不大,显示出政策并没有在实践中得到有效的优化与改进,应该深入实际,针对各企业的不同情况细化政策的实施准则,以改变这种不力的状况。
[1]王良举,陈甬军.集聚的生产率——来自中国制造企业的经验证据[J].财经研究,2013(1):49-60.
[2]孙隆英.高新技术企业所得税优惠政策执行中的几个问题[J].税收实务,2013:66-69.
[3]曹海娟.产业结构对税制结果动态响应的区域异质性——基于省级面板数据的pvar分析[J].财经研究,2012,(12):26—35.
[4]连玉君.中国上市公司投资效率研究[M].北京:经济管理出版社,72-82.
(责任编辑:胡忠任)
F276.44
A
2095—7416(2014)01—0100—04
2014-01-12
李延晨(1993-)男,山东济南人,山东大学商学院金融学系2011级本科生。

