无界域二次规划问题的区间算法
杨东,芮文娟
(1.中国电信徐州分公司,江苏徐州221000;2.中国矿业大学理学院,江苏徐州221000)
无界域二次规划问题的区间算法
杨东1,芮文娟2
(1.中国电信徐州分公司,江苏徐州221000;2.中国矿业大学理学院,江苏徐州221000)
利用罚函数将无界域二次规划问题转化为无约束优化问题,讨论了罚函数的区间扩张,利用Moore二分法与无解区域的删除原则,给出了求解无界域二次规划问题的区间算法。理论分析和实例计算均表明算法是可靠和有效的。
二次规划;区间算法;罚函数
0 引言
二次规划问题是一类重要的非线性规划问题。一方面来自于实际问题,出现在很多应用领域内,如最优控制、工程设计、证券投资决策及最小二乘问题等;另一方面,它具有重要的理论价值,例如,它常常作为子问题,出现在一般非线性规划问题的求解中。近来,对于凸二次规划,人们进行了比较深入的研究,给出的方法也非常有效。这些算法大都采用“有效集”策略,通过逐次求解等式约束二次规划问题来逼近最优解。1984年Karmarkar[1]首次提出了多项式时间算法,随着线性规划、驻点问题和线性互补问题的进一步深入研究,对二次规划的研究也进入了一个新的阶段。这些新的研究结果与同伦延拓算法、内点法有着密切的关系[2-3]。
区间算法是研究数值问题的一类重要的方法[4-11]。本文以区间数学为工具,研究和建立求解二次规划问题的区间算法。
本文主要考虑如下无界区域上的二次规划问题

式中:H∈Rn×n是对称矩阵;A∈Rm×n为行满秩矩阵;b∈Rm;d∈Rn。
记X(0)=Rn,则式(1)可记作


对本文所讨论的任意区间X,X的中点、宽度、半径和绝对值分别以m(X)、W(X)、R(X)和|X|表示。如果函数f(x)和区间函数F(X)满足f(x)∈F(X)(∀x∈X),则称F(X)是f(x)的区间扩张。
1 罚函数的区间扩张

其中:t(x,β)=f(x)+βg(x)为罚函数;β>0是罚因子。
以Sx表示问题(1)的最优点集。若x(β)是式(3)的一个解,并且x(β)→x∗(β→+∞),则x∗∈Sx。
定义t0:
t0(x,β)=

则式(3)可转化为

下面建立t0(x,β)的区间扩张。对任意X∈I(X(0)),取F1(X)为f(x)的自然区间扩张

取F2(X)为f(x)的中值型区间扩张

取Gj(X)为gj(x)的自然区间扩张

定义

对任意X∈I∞(X(0)),定义

定理1T1(X,β),T2(X,β)分别是t(x,β)的区间扩张。
证明先证明T1(X,β)是t(x,β)的区间扩张。
对任意x∈X∈I(X(0)),因为F1(X),Gj(X)分别是f(x),gj(x)区间扩张,所以有

所以

故T1(X,β)是t(x,β)的区间扩张。
同理可证明T2(X,β)是t(x,β)的区间扩张。证毕。


定理3对任意Z∈I(X(0)),设X∈I(Z),则当W(X)→0时W(T2(X,β))→0。

从而
W(((X-m(X))T(HX+d))i)→0(i=1,2,···,n)
由式(7)知
W(F2(X))=W((X-m(X))T(HX+d))→0
由式(9)知
W(T2(X,β))=W(F2(X))+βW(G(X))
所以只要证W(G(X))→0即可。
事实上,当W(X)→0时,

记

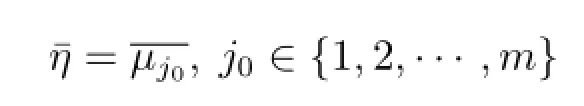
则

所以

所以当W(X)→0时W(T2(X,β))→0。证毕。
2 无界区域上的区间运算
2.1 无界区间的宽度和二分
在建立求解无界区域二次规划问题的区间算法之前,必须先定义无界区域的宽度和中点计算公式。设0<λ<∞为常数,λ通常可以这样选取:如果怀疑最优解存在于[-λ0,λ0]n中,则取λ=λ0。这样就能将[-λ0,λ0]n外的区域尽快地删除掉。


2.2 无界区间上的运算
设A,B∈I∞,以∗表示+、-、×运算,定义

定义A/B为包含{a/b:a∈A,b∈B,b/=0}的最小区间。
3 删除原则
无解区域删除原则在问题的研究中可以大量排斥无解子区域,降低存储量,减少计算成本,算法的收敛速度也可以加快。

这就是中点检验。

当KX/=∅时,令当KX=∅时,令
4 算法
算法的步骤如下:
(2)如果列表为空,转步骤(10)。
(3)从列表中取出第一项元素(X,TI,tM,KX),把它从列表L中删除,令β=β0,B=min{B0,TI}。
(4)如果tM-B<ε,转步骤(9)。
(5)计算Gj(X)(j=1,2,···,m)。若有j满足Gj(X)>0,转步骤(2);否则,令β=0。
(6)按照X最大宽度分量方向二分X得X(1), X(2)。
(7)
①l=1。
②i=1。
④i=i+1;若i≤n,转③。
⑤令X=X(l),计算TI,tM,KX,将(X,TI,tM,KX)按TI从小到大的顺序放到列表L中,令t0=min{t0,tM}。
⑥若l=2,转步骤(8);否则令l=2,转②。
(8)从列表L中删除所有满足TI>t0的项,转步骤(2)。
(9)输出[TI,tM],X,令B0=B,转步骤(2)。
(10)结束。
设式(5)的最优值为t+,最优解集为X+,由定理3和文献[1]中的定理2,可知有如下结论。
定理4如果上述算法经过n次循环后,列表L中只包含有界区域,则当n→∞时,TI→t+, tM→t+,X→X+。
对于式(3),由文献[1]知有如下结论。
定理5若式(5)的最优值t+=-∞,则式(3)无最优解,且无下界。
若式(5)的最优值t+∈R,X∗=X+∩Rn非空,则式(3)有最优值t∗=t+和最优解X∗。若X∗=∅,则式(3)没有最优解,但式(3)有下界。
5 算法的计算机实现
在编程进行算法实现的时候,采用下面的方法来处理无界区间。
设M是计算机所能表示的最大实数,以RM表示所有的机器数。
记

称IM为有限机器区间,¯IMIM为无限机器区间。
在无界区间进行计算时或构造区间扩张时,按如下方法处理:


假定程序n次迭代后终止,则这时可得到t+=-∞或是输出[TI,tM],X。对于输出结果,根据定理5和式(11),可以做出这样的结论:
(1)若t+=-∞,则t(x,β)无下界,式(3)无最优解。
(2)若X,[TI,tM]均是有限机器区间,则式(3)有最优解和最优值。
(3)若[TI,tM]或X为无限机器区间,则不能判别式(3)是否有解。
6 数值结果
依据上述算法,利用Matlab6.0编程进行数值实验,可得如下数值结果,其中X(0)表示初始区域,ε表示计算精度,β表示罚因子。

X(0)=R2,其最优解为:最优值为f∗=-7.2。
用上述区间算法计算输出的第一个结果是(ε=10-5,β=103):


用上述区间算法计算输出的第一个结果是(ε=10-4,β=102):

[1]KARMARKAR N.A new polynomial-time algorithm for linear programming[J].Combinalorica,1984,4(4):373-395.
[2]HAN C G,PARADOS E,YE Y.On the solution of indefinite quadratic program using an interior point algorithm [J].Informatica,1991(3):474-496.
[3]HUANG Z Y.An intrval entropy penalty method for nonlinear global opitimization[J].Reliable Computing,1998, 4(1):15-25.
[4]RATSCHEK H,ROKNE J.New computer methods for global optimization[M].Chichester:EuisHorwood Limited,1988.
[5]MOORE R E.Methods and applications of interval analysis[M].Philadelphia:SIAM,1979.
[6]曹德欣,沈祖和.一类非光滑优化问题的区间算法[J].高等学校计算数学学报,1998,20(1):23-33.
[7]曹德欣,叶帅民,王海军.An interval maximum-entropy method for a class of constrained nondifferentiable optimization problems[J].运筹学学报,1999,3(4):55-64.
[8]高岳林,徐成贤.边界约束非凸二次规划问题的分枝定界方法[J].运筹学学报,2001,5(4):81-89.
[9]曹德欣,李苏北,吴彦强,等.求连续minimax问题整体解的区间算法[J].高等学校计算数学学报,2002,24(4): 359-365.
[10]沈祖和.区间分析方法及其应用[J].应用数学与计算数学学报,1983(2):1-29.
[11]王海军,曹德欣,李苏北,等.非线性等式约束全局优化问题的区间算法[J].中国矿业大学学报,2003,32(2): 204-208.
An Interval Algorithm for Quadratic Programming in Unbounded Domains
YANG Dong1,RUI Wen-juan2
(1.China Telecom Xuzhou Branch,Xuzhou 221000,Jiangsu,P.R.China;2.School of Science,China University of Mining and Technology,Xuzhou 221000,Jiangsu,P.R.China)
By using the penalty function,the quadratic programming problems in unbounded domain are transferred to unconstrained optimization problems.The interval extension of penalty function is discussed.With no deletion of principle based on Moore dichotomy, the interval algorithm for solving quadratic programming problems in unbounded domain is established.Theory analysis and example calculation show that the algorithm is reliable and effcient.
quadratic programming;interval algorithm;penalty function
O221.7
A
1001-4543(2014)03-0239-06
2014-04-10
芮文娟(1979–),女,安徽亳州人,讲师,硕士,主要研究方向为非线性优化和非光滑优化问题的区间算法。
电子邮箱xzhzgya@126.com。
中央高校基本科研业务费专项资金(No.2013QNA33)资助

