基于PSO-ANFIS改进算法的推理系统平衡性研究
杨正校,刘静,汪小霞
(苏州健雄职业技术学院软件与服务外包学院,江苏太仓215411)
基于PSO-ANFIS改进算法的推理系统平衡性研究
杨正校,刘静,汪小霞
(苏州健雄职业技术学院软件与服务外包学院,江苏太仓215411)
针对粒子群优化(PSO)算法在自适应神经模糊推理系统(ANFIS)中的集成应用,提出对学习神经模型参数、隶属度函数参数进行改进优化的算法。该算法可增强模糊系统的近似精度和可解释性,提高系统的性能,进而发现更好的分类优化规则。算法经4个标准数据库的数据测试,结果表现出更好的性能,获得更好的分类效果,同时降低了系统时间复杂度。
自适应神经模糊推理系统;可解释性;精度;演化算法;粒子群优化
0 引言
神经模糊系统的强度涉及模糊建模中两个相互冲突的需求:近似精度和可解释性。在模糊系统理论或应用[1]中提高模糊系统的近似精度和可解释性是一个很重要的问题。基于TSK模型的自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System,ANFIS),是神经建模的特殊分支,其结构与一般神经模糊系统类似,从数据集中获取数据属性,并根据给定的误差标准调整系统参数[2]。但在规则层中,它有许多代表自动生成所有可能的神经模糊结构模糊规则的节点,而自动生成规则又有产生冗余规则的机会。因此,研究一种生成具有良好的准确性和有效规则的ANFIS同步技术是必要的。
粒子群算法,也称粒子群优化(Particle Swarm Optimization,PSO)算法,是近年来发展起来的一种新的演化算法[3](Evolutionary Algorithms,EA),由于其容易实现并且需要调整的粒子很少而为研究人员所广泛应用与开发。该算法受飞鸟集群活动规律的启发,利用群体智能建立一个简化模型[4]。此外, PSO算法只需要几行程序代码就可以实现,仅需要基本的数学运算符,运算速度快,内存消耗小[5-6]。文献[7]中通过设计规则,使用PSO来解决模糊神经网络(FNN)的冲突问题。
基于PSO算法的优点以及ANFIS的需求,本文通过优化隶属度函数确定神经模糊系统中相互冲突问题的平衡关系,对粒子群优化方法在ANFIS结构中增强平衡精度和可解释性的性能进行检验。
1 自适应神经模糊系统
与一般模糊模型结构类似,ANFIS主要通过两个特征指标来评估模糊模型的质量:可解释性和精度[8]。可解释性即用模糊模型来表示其系统的常规属性。一些研究者认为可解释性包括模型结构、输入变量的数目、模糊规则的数量、术语条款,以及模糊集的形态等内容,因为它会影响系统的复杂程度和处理时间,所以在ANFIS过程中是重要的问题。可解释性可以通过微调和改进模糊规则,如增加和减少模糊规则数目,从而在所有可能的模糊规则中找到更加有效的规则。
精度,能准确地表示模型系统的能力,模糊模型越接近真实系统,其精度越高,真实系统和模型系统响应的相似性能被模糊模型理解。神经模糊系统的优势之一就是能够完全基于近似和语言信息来进行设计。因此,通过调整网络结构和学习神经模糊模型的参数可以达到满意的精度[9]。在隶属度函数和精度之间有密切的联系[10]。依据这一结论,我们猜想:优化隶属度函数将会改进神经模糊系统的精度。
基于模糊建模中两个相互冲突的需求,ANFIS可以同时优化这两个需求目标。
(1)修改ANFIS的参数以获得良好的性能(精度),它是基于均方误差(Mean Square Error,MSE)的模糊建模,公式如下:

式中:yj和ydj分别表示网络输出值和输出期望值; N是数据总量。
(2)增加和减少模糊规则数量以获得一个可解释的模糊模型,公式如下:

式中:R是规则节点的最大值;Or(∈O,O表示模糊规则集)是用来确定是否存在规则节点r的二进制值,相当于开关,用来打开或关闭一个规则节点。
2 使用PSO修改自适应神经模糊系统
PSO算法是ANFIS作为一种学习方式优化两个相互冲突标准的演化算法的一部分,它的一种定义是把PSO描述成粒子群,而每个粒子代表一个潜在的解决方案。把PSO的学习机制引入模糊系统,将构成一个具有人类感知成分的自适应神经网络系统,在不知不觉中向训练数据学习,自动产生、修正并高度概括出最佳的输入与输出变量的隶属度函数以及模糊规则;另一方面,神经网络的各层结构与参数也都具有了明确的、易于理解的物理涵义[11]。
PSO是解决ANFIS问题的一个潜在技术。在PSO算法中,PSO是由粒子构成的,粒子的位置受其速度的影响。ANFIS被看作是一个粒子和参数,这些参数是影响ANFIS过程的粒子维度。设xi(t)为第i粒子经过时间t后在搜索空间的位置,通过增加速度来改变粒子的位置。若vi(t)代表当前位置,则有

式中:c1和c2是加速度;r1和r2是随机向量,pbest和gbest分别表示局部或全局最优值。
由此可见,粒子的数量等于ANFIS过程的数量,而每个ANFIS过程都是完成目标函数的一个潜在解决方案,图1是自适应神经模糊推理系统结构。图中:x表示输入信号,µ表示隶属度函数的前期函数, λ表示隶属度函数的后期参数,R表示模糊规则库, π表示标准化模糊规则,N表示自适应规则,k表示学习机制。

图1 自适应神经模糊推理系统结构图Fig.1 The adaptive neuro-fuzzy architecture
第1层是输入层,而xi(i=1,2,···,n)是输入信号;第2层是模糊化过程的前期参数即隶属度函数(µ),每个节点与第2a层的单节点相连,连接代表修改隶属度函数值;第3层是模糊规则库层;第4层是标准化层,在这一层中,将选择优化的模糊规则(o);第5层是去模糊化层,受结果参数(k)的影响;c是系统输出。
如图1所示,第2层中的每个节点与2a层有单个节点相连,意味着在第2层中的每个隶属函数参数将要在2a层中修改,从而获得适当的隶属参数,该隶属参数将用来测量输出并获得最小误差。此外,第3层的每个节点与第4层的每个节点相连,其中每个连接线代表一个模糊规则。最优模糊规则的选择取决于每个模糊规则在其对应系统中的重要性。
在PSO-ANFIS中,利用PSO调整所有ANFIS学习到的参数,增加和减少ANFIS结构中模糊规则数量,从而分别获得最佳参数值和模糊规则数。所提出的PSO-ANFIS将用最少的模糊规则和高性能的准确性来设计ANFIS。所以,这个任务是通过选择准确性高、规则数量少来完成的。
图2为PSO-ANFIS算法过程。下面通过PSO增减ANFIS结构中的模糊规则数以调整ANFIS的所有参数。

图2 PSO-ANFIS算法流程图Fig.2 The fow chart of PSO-ANFIS
设第i个粒子为Xi=(xi1,xi2,···,xid),这些粒子会在解空间搜索并跟踪2个“极值”:一是粒子本身所找到的最优解,也称为局部极值pbest,记为Pi=(pi1,pi2,···,pid);另一个是群体中所有粒子经历的最佳位置,或称为全局极值gbest,记为Pg=(pg1,pg2,···,pgd)。粒子i的速度表示为Vi=(vi1,vi2,···,vid),每一个粒子的位置就是一个潜在解[12],在每一次迭代中,根据下列步骤对速度进行更新。
(1)使用速度(vd)和d维度初始化粒子位置(xd)。
(2)对PSO-ANFIS适应度函数(fj)进行初始化,适应度函数是ANFIS的目标函数即式(1)和式(2)。
(3)使用式(1)和式(2)找到ANFIS的目标函数,根据适应度函数找到粒子的位置。如果适应度函数的位置比适应度函数的当地位置好,那么pbestd=xd。
(4)找到最好的pbestp值,把pbestp设置成gbest。
(5)使用式(3)和式(4)更新速度和位置。
(6)对于每个粒子,找到新的适应度函数fxi,基于步骤(3)确定新的适应度函数值,基于步骤(4)找到gbest值。
(7)判断数值如果收敛,则停止,否则返回步骤(5)检查,直至迭代完成并产生最优值,则过程结束,否则转到步骤(5)。
3 算法实验与对比分析
为了评估上述算法的性能,进行标准数据库数据实验,所用数据选自加州理工学院机器学习数据库UCI机器学习网站(http://archive.ics.uci.edu/ ml/datasets.html)的学习数据库:Iris Flower,Balloon, Haberman’s Survival Data and Thyroid。表1汇总了本实验中使用到的数据集属性。

表1 数据集属性Tab.1 Characteristics of datasets
为确保数据的一致性,数据集的数值采用正常范围内([0,1])的数值,对系统进行交叉性实验。将数据集随机地划分为训练组和测试组两个部分,其中80%的数据作为训练组,其余20%作为测试组。训练组的目的是为了训练网络获取ANFIS的学习数据,测试组是用来测试ANFIS的表现且不出现在训练过程的数据。
表2给出了PSO-ANFIS过程中参数的初始值。对每个数据集进行1 000次实验,以测试均值和标准差是否分别满足精度要求,计算并给出规则数量和时间消耗。

表2 技术参数Tab.2 Specifcation of proposed method
选取粒子数为50,语言模糊集数为3,c1=0.5, c2=1,迭代次数为103,对均值误差和标准差误差进行仿真比较,运行结果如图3所示。

图3 算法改进前后的误差仿真对比图Fig.3 The simulation comparison chart
表3给出了ANFIS基于PSO算法学习到的平均值和标准差,表中显示的最佳误差率发生在训练过程中的Balloon组,而测试过程的最佳错误率发生在Iris Flower组。结果表明,误差率不受输入参数数量和样本的影响,但与数据集本身的分布有关,尽管Haberman的数据集有3个输入变量,但其分类的分布极其不平衡(有一级实例255个和二级实例81个),因此,比较Balloon组和Iris Flower组,都出现了较大误差。Balloon组的实例相对较少,而其他组的分布数据相对正常,训练组和测试组的误差结果存在巨大差异。相反,Iris Flower组的数据变量比Haberman组多,比Balloon有更多的实例,但其数据分布正常,输出显示了训练组和测试组的最小误差值,尽管Thyroid组比其他组具有更多的变量,其数据结果显示非正态分布。因此,可以得出结论:每个类别的数据分布对误差率产生较大的影响。
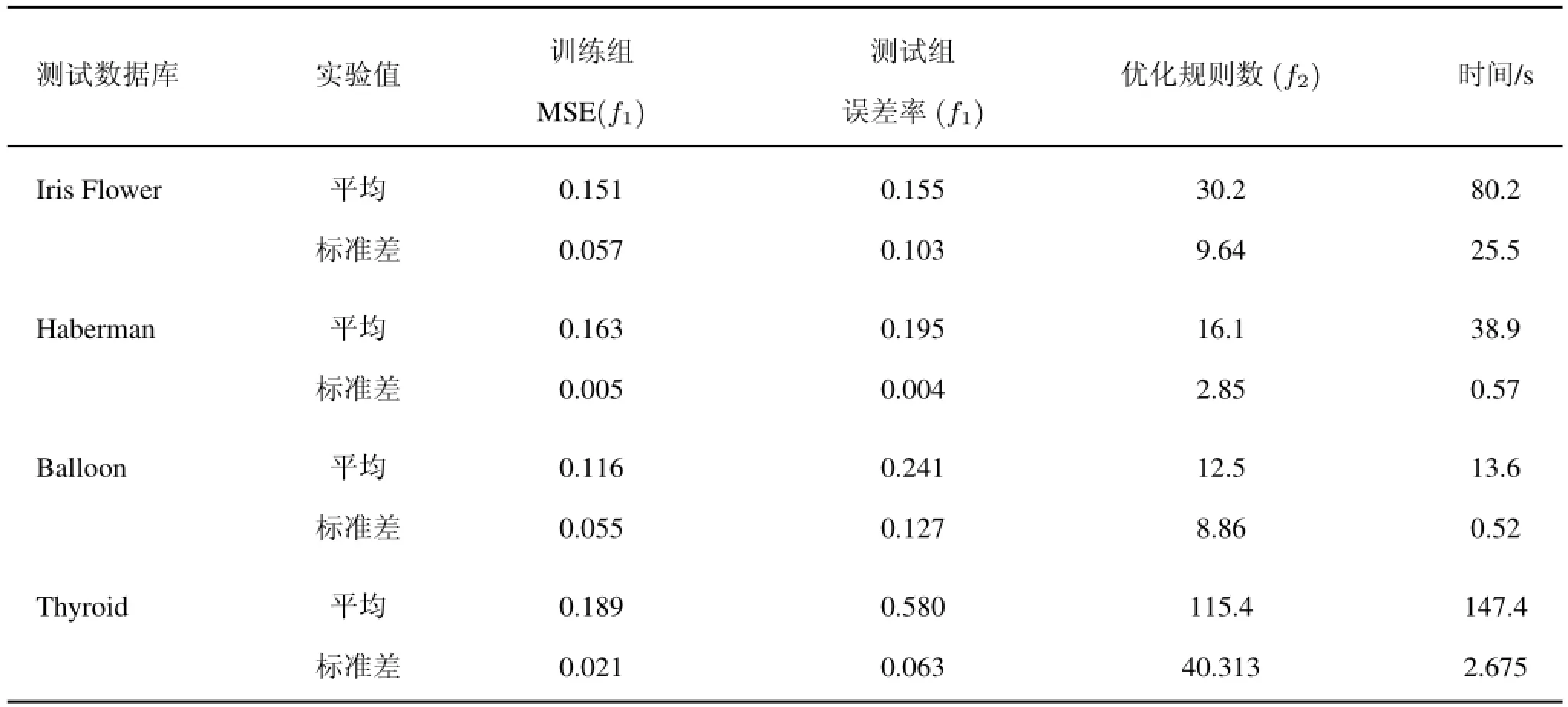
表3 PSO-ANFIS实验结果Tab.3 Result of PSO-ANFIS
在优化规则数(f2)列中,数量最小的是Balloon组,而Thyroid组获得的优化规则数量最多。从表3中可见,Balloon组数据集最小,Thyroid组数据集最大,似乎输入数量和优化规则之间存在关联。然而, Haberman组的输入数据量比较少,而优化规则数量却比Balloon组多。从样品(实例)的数量看,Haberman组的实例数量比Balloon组多,而Iris Flower组具有更多优化规则数,这是由于输入Haberman组,并且比Balloon组具有更多的实例。因此可以得出结论:输入数量和实例是发现优化规则数的决定因素。
表3同时给出了时间与规则数量的平衡关系,规则数量与时间成正相关。Balloon组与其他组进行比较,优化规则数少,时间开销也较小。Thyroid组比其他组优化规则多,时间消耗多。由此可以得出结论:时间复杂度的减小取决于优化规则的数量。
评价PSO-ANFIS的测量分类可以通过灵敏性、特异性和表4中执行的模型预测精度的平均值得到。表4表明,当敏感性较高而特异性较低的时候,准确性更高,说明测量分类的准确性与灵敏性、特异性这两个值之间存在着对应关系。在这个结果中,获得分类精度最高的是Balloon组(分类精度等于所有数据集精确分类后的准确性平均值),Iris Flower组和Haberman组分列第二和第三,精度最不理想的是Thyroid组。通过数据分析显示,与Haberman组相比较,Iris Flower组,Balloon和Thyroid组有较多的输入变量和较少的实例,但分类精度比Haberman组的高。Haberman组与其他组相比,其中每个类别数据集的分布都呈非正态分布,可见每个类别的数据分布可能对数据集以外的不一致的数据集分类产生较大影响。实验结果对所有数据集给出的可行的准确性分类的精度都超过了75%。

表4 方法的测量分类Tab.4 Classifcation measurement of Proposed method
4 结语
本文通过对群智能优化算法(PSO)进行改进,将其用于自适应神经模糊推理系统(ANFIS)实现性能优化。本文的创新之处是:基于在可解释的基础上提高精度和降低时间复杂度两条准则,对ANFIS架构进行优化,并使用标准数据集进行测试。测试结果表明:该算法对所有数据集给出的可行的准确性分类的精度都超过了75%,降低了时间复杂度,从而提高了算法的效率。
参考文献:
[1]PAIVA R P,DOURADO A.Interpretability and learning in neuro-fuzzy systems[J].Elsevier Fuzzy Sets and Systems, 2004,147:17-38.
[2]NEGNEVITSKY M.Artifcial inteligence:A guide to intelligent systems[M].2nd ed.England:Pearson Education Limited,2005.
[3]郑金兴.粒子群优化人工神经网络在高速铣削力建模中的应用[J].计算机集成制造系统,2008,14(9):1710-1716.
[4]顾秀萍.自适应神经模糊推理系统(ANIS)及其仿真[J].火力与指挥控制,2010,35(2):48-53.
[5]Bai Q.Analysis of particle swarm optimization algorithm [J].Computer and Information Science,2010,3(1):180-184.
[6]ENGELBRECHT A P.Fundamental of computational swarm intelligent[M].London,England:John Wiley&Sons Ltd,2005.
[7]MA M,ZHANG L B,MA J,et al.Fuzzy neural network optimization by a particle swarm optimization algorithm[C]//Advances in Neural Networks.Berlin,Heidelberg:Springer Berlin Heidelberg,2006,3971:752-761.
[8]DI NUOVO A G,CATANIA V.Linguistic modifers to improve the accuracy-interpretability trade-off in multiobjective genetic design of fuzzy rule based classifer systems[C]//2009 Ninth International Conference on Intelligent Systems Design and Applications.USA:Intelligent Systems Design and Applications,2009.
[9]LEE C H,TENG C C.Fine tuning of membership functions for fuzzy neural system[J].Asian Journal of Control, 2001,3(3):216-225.
[10]ZENG X J,SINGH M G.A relationship between membership functions and approximation accuracy in fuzzy systems[J].IEEE Transactions on Systems Man and Cybernetics.Part B:Cybernetics,1996,26(1):176-180.
[11]王介生,张勇.基于ANFIS的软测量模型在浮选中的应用[J].合肥工业大学学报:自然科学版,2006,29(11): 1365-1369.
[12]朱炜,贾衡天,徐玉如,等.水下目标的特征提取及识别[J].系统工程与电子技术,2008,30(1):171-175.
Research on Reasoning System Balance Based on the Improved Algorithm PSO-ANFIS
YANG Zheng-xiao,LIU Jing,WANG Xiao-xia
(School of Software and Service Outsourcing,Suzhou Chien-shiung Institute of Technology, Taicang 215411,Jiangsu,P.R.China)
For the particle swarm optimization(PSO)algorithm on the adaptive neuro fuzzy inference system(ANFIS)integrated applications,put forward an improved algorithm by optimizing the learning of neural model parameters,the parameters of membership functions.The algorithm can improve the approximation accuracy and interpretability of fuzzy systems and the performance of the system.The proposed method has been tested on four standard dataset from UCI machine learning,i.e.Iris Flower,Haberman’s Survival Data,Balloon and Thyroid dataset.The results have shown better classifcation using the proposed PSO-ANFIS and the time complexity has reduced accordingly.
adaptive neuro-fuzzy inference system(ANFIS);interpretability;accuracy;evolutionary algorithms;particle swarm optimization(PSO)
TP301.6
A
1001-4543(2014)03-0233-06
2014-04-03
杨正校(1963–),男,江苏沭阳人,副教授,硕士,主要研究方向为算法与软件设计、职业教育研究。
电子邮箱yzx new@163.com。
江苏省教育厅2013年度高校哲学社会科学基金(No.2013SJD880071)资助

