基于Halbach 阵列的水轮发电机组永磁悬浮承重装置

梁 欢，马宏忠，王庆燕，姜鸿羽

(河海大学能源与电气学院，南京市210098)

0 引 言

大中型立轴式水轮发电机组运行时，轴负荷全部由推力轴承承担，巨大的轴向负荷容易破坏油膜，导致轴承瓦烧毁，需要停机换瓦，而烧瓦的最根本原因就是摩擦问题［1］。为了解决这个问题，文献［2-4］提出了针对立轴式水轮发电机组的混合磁悬浮承系统，利用永磁体装置的推力与电磁体装置的吸力，共同承担整个发电机组大部分的轴向负荷(自重和机组轴向的水推力等)，大大减轻了机械推力轴承所承受的压力负荷，进而可以使所需要的大型推力轴承的要求得到减小并降低了各种机械损耗。从而，从根本上解决了传统推力轴承在长期重负荷下所引起的轴瓦机械变形、发热、磨损和机械老化等问题，降低了水轮发电机组的机械故障发生率，对延长机组无故障使用寿命的提高起到了积极的作用。

在季节、水头高度和水流量大小等环境因素变化时，机组轴向水推力也会随之改变。通过调节电磁悬浮装置的励磁电流来调节电磁悬浮力的大小，以使整个混合磁悬浮系统承载能力与水轮发电机组的实际轴向负荷相适应。

永磁悬浮装置可以在一定程度上减小电磁悬浮装置的励磁电流和对电磁悬浮装置的要求，从而减小电磁悬浮装置的损耗和发热问题。考虑到水轮发电机组运行的稳定性，本装置并不使转子系统全浮起，而是只承担约80%的轴向负荷(永磁悬浮装置承担48%，电磁悬浮装置承担32%)，这样既可以从根本上减少施加在推力轴承上的轴向负荷，减小了推力轴承与轴瓦之间油膜的磨损，又可以保证发电机组转动部分运行稳定。

文献［2］提出的永磁悬浮装置体积很大，但实际安装空间有限导致安装困难，基于此项不足，本文采用Halbach 圆环阵列结构对永磁悬浮装置进行改进，并用有限元分析软件ANSYS10.0 软件对其进行三维模型承载力分析。

1 Halbach 阵列永磁悬浮装置

1.1 混合磁悬浮装置介绍

文献［2-4］提出的混合磁悬浮水轮发电机组转子承重系统是主要针对大中型立轴轴流反击式水轮发电机组设计的，根据此类水轮发电机组的特点，采用永磁悬浮和电磁悬浮2 部分共同对水轮发电机组整体施加向上的悬浮力，如图1 所示。

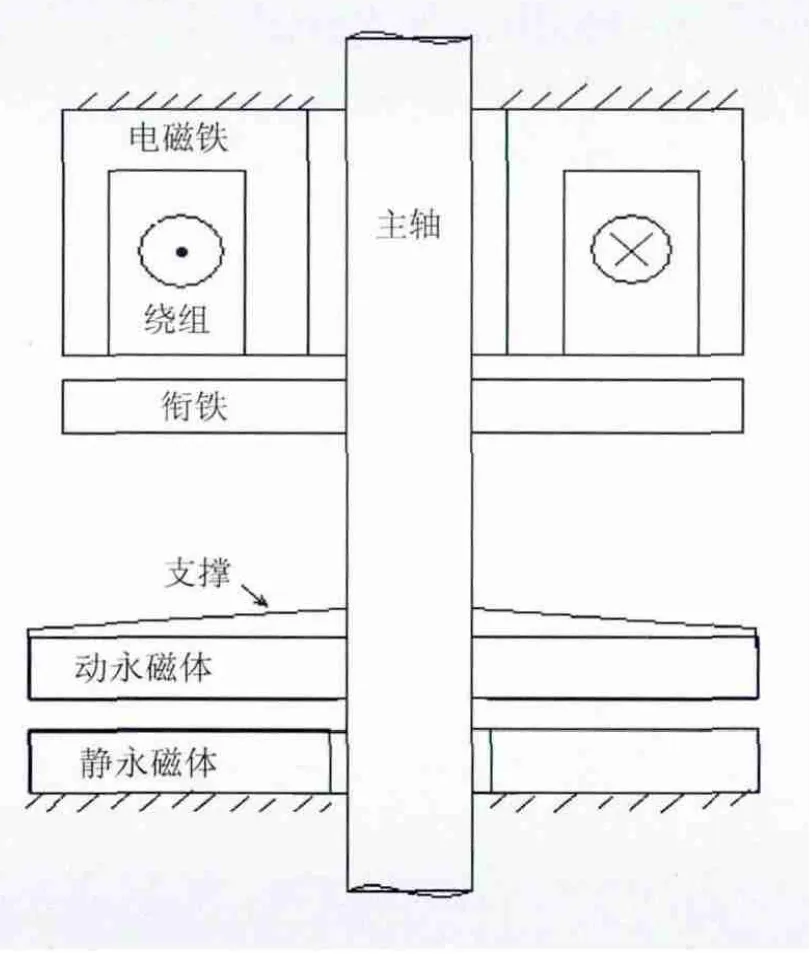
图1 水轮发电机组转子系统磁悬浮承重示意Fig.1 Illustration of magnetic levitation rotor weight support system for hydraulic turbine generator units

永磁悬浮部分由动永磁体和静永磁体组成，电磁悬浮部分由电磁铁、衔铁以及绕组组成。动永磁体和衔铁与主轴连接在一起，静永磁体下部和电磁铁上部与土木建筑物连接，这样，轴向承载力则会传递到土建设施，推力轴承压力负荷得到减小。

1.2 Halbach 阵列介绍

Halbach 阵列是一种磁体结构，是工程上的近似理想结构，目标是用最少量的磁体产生最强的磁场。利用特殊的磁体单元排列，可以增强阵列一侧的磁场而减弱另一侧的磁场，其中强侧磁场具有良好的正弦性［5］。工程用直线型Halbach 阵列永磁体如图2(a)所示，其对应的轴截面磁通如图2(b)所示。

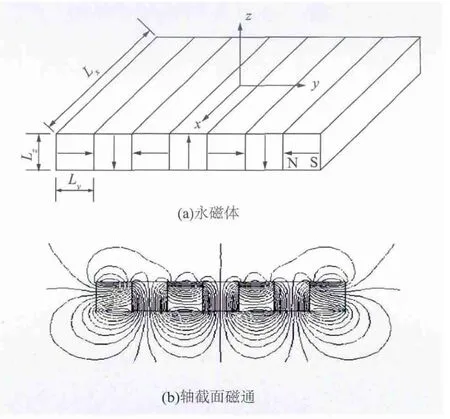
图2 工程用直线型Halbach 永磁阵列Fig.2 Engineering used Halbach permanent magnet linear array

工程上还经常采用环形Halbach 阵列永磁体结构，由径向极化和轴向磁化的永磁体环拼接而成，已经应用到工业磁轴承系统和电磁悬浮系统［6］。

1.3 Halbach 阵列永磁悬浮装置

本文将一块按预设方向磁化的磁环单元径向拼接制造好的Halbach 阵列永磁体环固定于主轴适当位置(如主轴下半部分某位置，由实际空间决定)，并在水轮发电机转轮与该永磁体环之间建造1 层土木建筑物(或其他支撑物)，其上置另1个相同尺寸的按预设方向磁化的磁环单元径向拼接制造好的Halbach 永磁体环，并使这2 块永磁体环相斥，那么土木建筑物将力传递给土建设施，永磁悬浮装置就对主轴施加了向上的悬浮推力，见图3(a)。预设磁化方向的磁体单元排列轴截面右半部分如图3(b)所示。

安康水电站位于陕西省安康市上游18 km 的汉江上［7］，安装了4 台型号为SF －200 －56/12800、额定功率为200 MW 的水轮发电机组(额定电压13.8 kV，额定电流9 560 A，额定转速107.1 r/min)，总装机容量800 MW。发电机组为装有上导轴承的半伞式结构，顶部装有直径达5.4 m 的大型同轴交流励磁发电机，额定容量为2.5 MVA。水轮机型号为HL － 220-LT － 550，转轮直径5.5 m，平均水头76.2 m。该水电站转子系统采用传统推力轴承支承方式，其推力总负荷为1 600 t。整个发电机组的承重不仅包括转轮、主轴、发电机转子以及蜗壳上部部分混凝土的重量，还有随水流量变化的轴向水推力，文献［2］计划设计混合磁悬浮装置提供约占承重总负荷的80%，约为1 280 t。永磁悬浮装置与电磁悬浮装置各承担48%和32%，即永磁悬浮装置承担542 t，电磁悬浮装置承担418 t。永磁悬浮装置由2个材料、尺寸均相同的径向磁化永磁环组成，本文初步设计的Halbach 阵列永磁悬浮装置采用的2个永磁环均由7个径向长度相同的永磁体环单元径向拼接组成，拼接后的永磁环保持原来的尺寸，以便进行承载力结果比较，装置尺寸见表1。

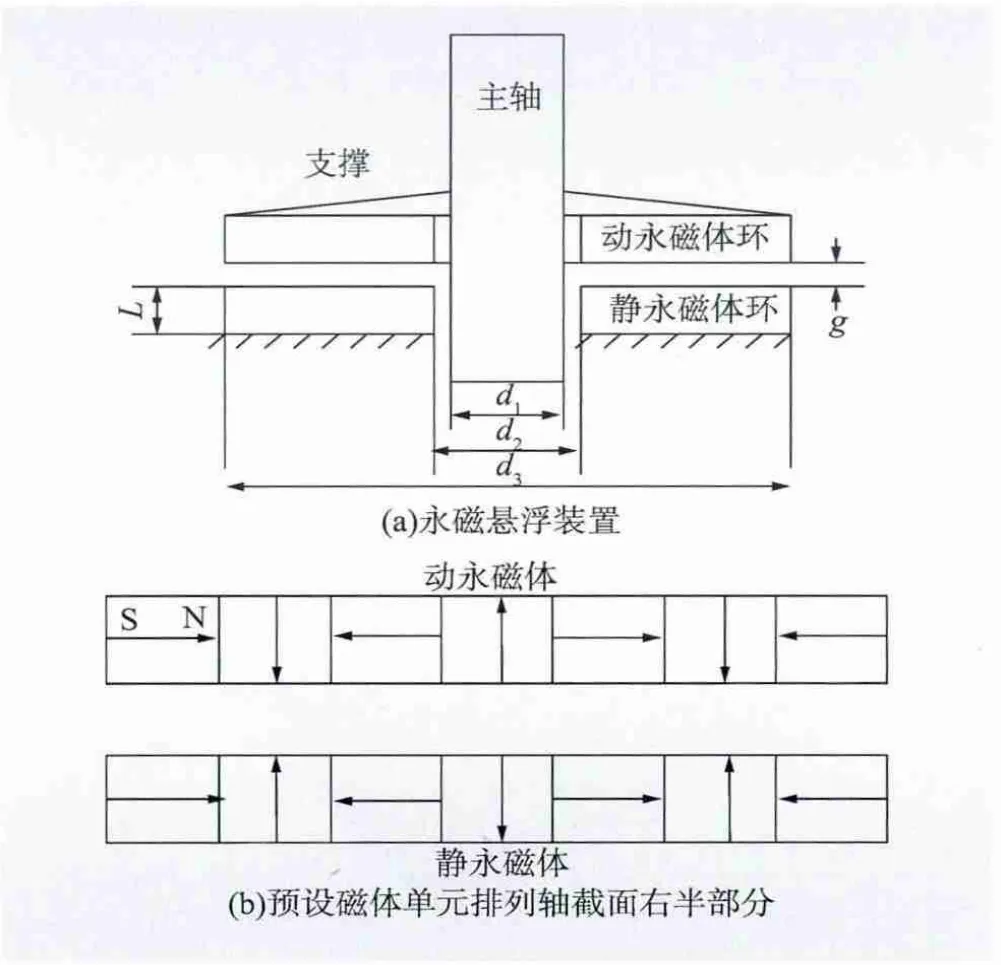
图3 Halbach 阵列永磁悬浮装置结构示意Fig.3 Structure diagram of permanent magnetic levitation device with Halbach array

表1 Halbach 阵列永磁悬浮装置尺寸Tab．1 Size of permanent magnetic levitation device with Halbach array

2 有限元分析

2.1 三维电磁场的数学模型

电磁场理论由一套麦克斯韦方程组描述，分析和研究电磁场的出发点就是麦克斯韦方程组的研究［8］。微分形式的麦克斯韦方程组为

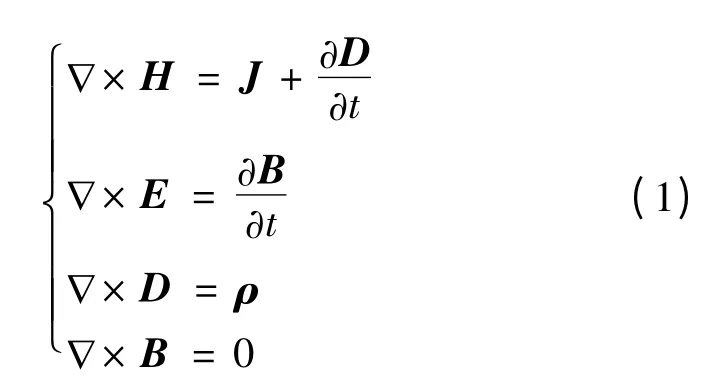
式中:H 为磁场强度，A/m;J 为传导电流密度矢量，A/m2;D 为电通密度，C/m2;E 为电场强度，V/m;B为磁感应强度，T;ρ 为电荷体密度，C/m3。

电磁场计算中，通常要对上述偏微分方程进行简化，以便能够用格林函数法、分离变量法等方法得到电磁场的解析解，其解的形式为三角函数的指数形式以及一些用特殊函数(如勒让德多项式、贝塞尔函数等)表示的形式。但在工程实践中，要得到精确问题的解析解通常是很困难的。于是只能根据具体情况给定的边界条件和初始条件，用数值解法求得其数值解，有限元方法就是其中最有效、应用最广泛的一种数值计算方法。

对于电磁场的计算，为了使问题得到简化，定义2个量来把电场和磁场变量分离开，分别形成一个独立的磁场或电场偏微分方程，这样便有利于数值求解。这2个量一个是矢量磁势A，另一个是标量电势φ，分别为

代入(1)中，经过推导可得

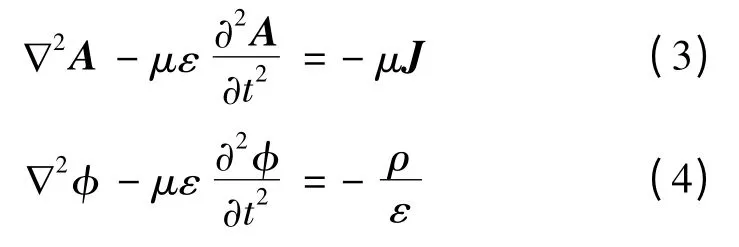
式中:μ 和ε 分别为介质的磁导率和介电常数。

本文只对静态磁场进行分析选择磁场矢量A 为求解函数，轴对称场中，J 和A 只具有θ 坐标分量，其边值问题为

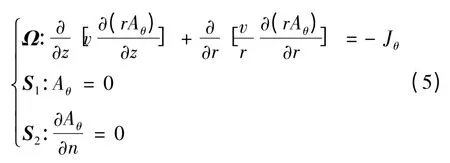
式中:Ω 为求解场域;S1为建立模型的边界，在其上满足Bn=0，即第一类齐次边界条件Aθ=0;区域内空气隙与铁磁物质交界处满足Ht=0，为第二类齐次边界条件∂Aθ/∂n =0，其余Aθ=0;ν 为磁阻率，H/m;Jθ为源电流密度，A/m2［9］。

式中:

求解得到磁势的场分布值后，即可相应得到磁感应强度、磁力等物理量。

2.2 仿真模型建立、仿真结果显示

本文采用ANSYS 10.0 进行仿真计算，具体建模仿真步骤［10］如图4 所示。

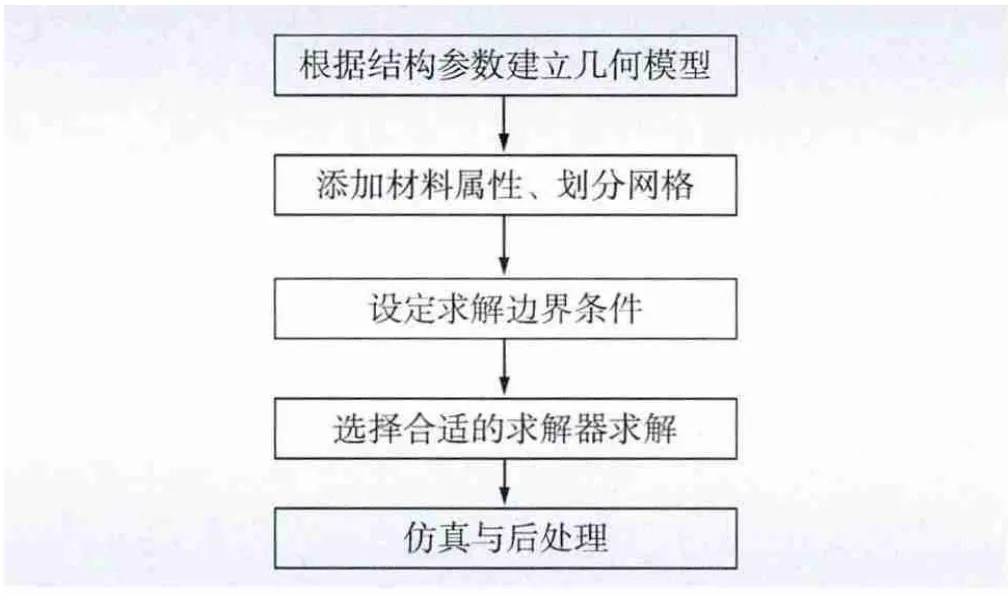
图4 ANSYS 建模仿真流程图Fig.4 Simulation flow chart of ANSYS modeling

采用三维实体单元SOLID96(三维磁实体标量单元，节点数为8，砖形形状)对所有物理区域进行建模并用空气包围起来，由于模型为轴对称的，这里只建立1/4 模型进行分析，实际轴向承载力为1/4 模型仿真结果的4 倍。

本文永磁悬浮装置采用的永磁体材料为钕铁硼稀土合金材料，其剩余磁感应强度Br=1.5T，矫顽力Hc=1 200 kA/m，永磁体相对磁导率μr=Br/(μ0×Hc)=1.5/(4π ×10－7×1 200 000)=0.994 7，同时其最大磁能积的极限值可达475 kJ/m3。主轴材料为锻钢材质，相对磁导率定义为1 000。

(1)根据结构参数建立模型并划分网格。在ANSYS 10.0 中按表1 建立几何模型，再给各个体赋予对应的材料属性(这里主要指磁导率)，最后再进行3 级精度网格划分，得到有限元模型如图5 所示。

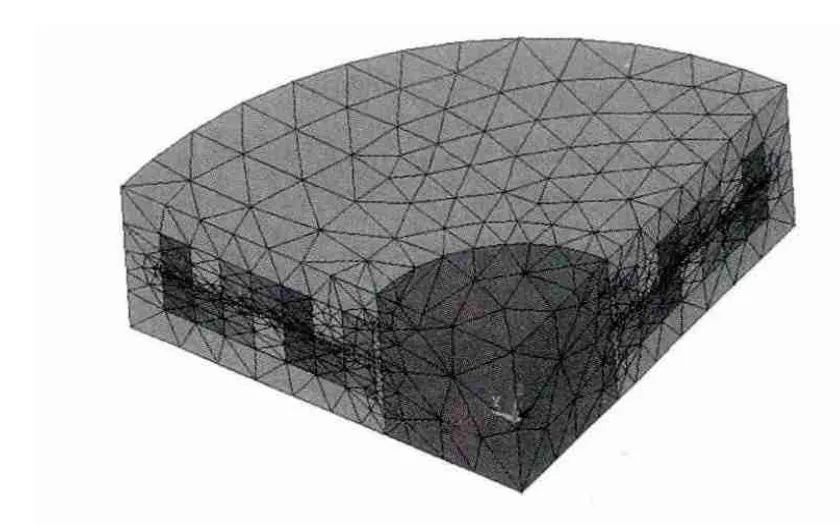
图5 Halbach 阵列永磁悬浮装置有限元模型Fig.5 Finite element model of permanent magnetic levitation device with Halbach array

(2)设定求解边界条件。选择主轴和连接与主轴的推力盘区域的有限元单元，创建1个组件，定义为arm，并施加力的标志，以便显示力的结果。对于三维仿真，由于软件自动对外围节点施加磁力线平行条件，因而这里不需要再施加边界条件。

(3)选择合适的求解器求解。以上步骤完成后，选取所有实体进行静态磁场计算，采用简化标势法进行求解。

本次实习在3周时间里强化学生综合实践能力，对《网页设计与制作》、《动态网站开发》和《.NET企业级应用开发》等课程的知识整合与能力提升具有极大促进作用。每组结合兴趣点自定义项目，充分调动学生积极性。共同开发锻炼了学生的沟通能力和团队合作能力。通过工作日报、工作汇报与成果展示等检验环节，5组都完成了预定目标。

(4)仿真与后处理。求解完毕后通过后处理模块查看磁感应分布云图和承载力分布矢量图。图6(a)和图6(b)分别为1/4 动永磁体上表面和下表面磁密分布云图;图7 为承载力分布矢量图。

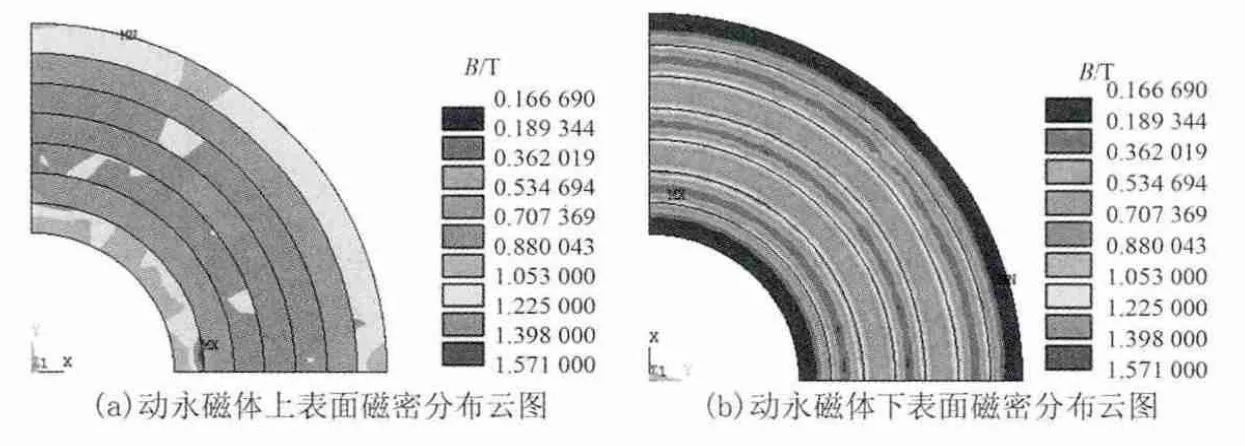
图6 动永磁体上、下表面磁密分布云图Fig. 6 Magnetic flux density distribution on upper and under surface of moving permanent magnet

图7 承载力分布矢量图Fig. 7 Vector distribution of bearing force

调用通用后处理模块查看作用在arm 上的力可以发现，Halbach 阵列永磁悬浮装置在与原装置在相同尺寸下，能提供约1 600 t 的承载力，可见承载力得到极大的提高。因而可以通过研究承载力与装置结构尺寸的关系，减小装置体积满足安装要求，并且能够有效节约成本。

2.3 承载力与Halbach 阵列永磁悬浮装置结构尺寸的关系分析

2.3.1 承载力与永磁体环轴向长度的关系

改变表1 中永磁体环轴向长度大小，其他尺寸保持不变，建立不同永磁体环轴向长度L 的永磁悬浮装置模型，仿真得到承载力随永磁体环轴向长度变化的曲线见图8(a)。从图8(a)可以看出，承载力随着永磁体环轴向长度的增加而增大，但当永磁体环轴向长度增加到一定长度，承载力增加的速度会明显减小，即承载力增加趋于饱和。可以近似认为在永磁体环轴向长度在小于径向长度范围内，与承载力成线性关系。

2.3.2 承载力与永磁体环间气隙长度的关系

改变表1 中气隙长度大小，其他尺寸保持不变，建立不同气隙长度g 的永磁悬浮装置模型，仿真得到承载力F 随永磁体环轴向长度变化的曲线见图8(b)。从图中可以看出，承载力随永磁体环间气隙长度的增加而减小，且基本成线性关系。

2.3.3 承载力与永磁体环单元径向长度的关系

改变表1 中永磁体环单元径向长度大小，其他尺寸保持不变，建立不同永磁体环单元径向长度l 的永磁悬浮装置模型，仿真得到承载力F 随永磁体环单元径向长度变化的曲线见8(c)。从图中可以看出，承载力随永磁体环单元径向长度的增加而增大，且基本成线性关系。

2.3.4 承载力与永磁体环相对磁导率的关系

保持表1 中尺寸和永磁体环材料剩磁大小不变，建立不同永磁体环相对磁导率μr的永磁悬浮装置模型，仿真得到承载力F 随永磁体环轴向长度变化的曲线见图8(d)。从图中可以看出，承载力随永磁体环相对磁导率的增加而减小。

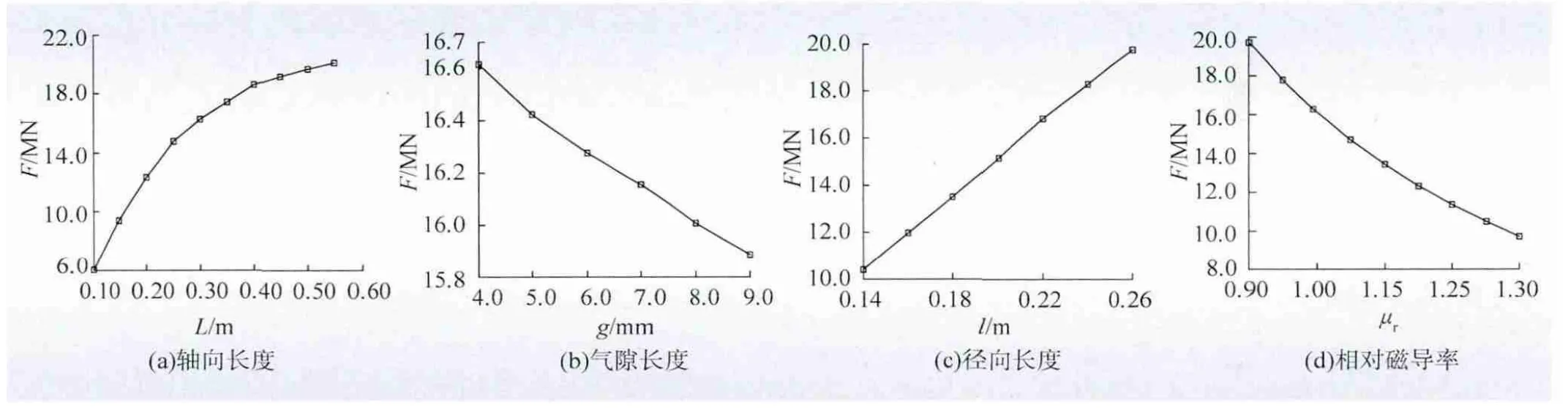
图8 承载力与永磁环结构尺寸的关系Fig.8 Relationship of bearing force with structural size of permanent magnet ring

2.4 尺寸参数选择

在选定好永磁材料(即相对磁导率确定)后，主要可以通过以下方法减小Halbach 阵列永磁悬浮装置提供的承载力:(1)减小永磁体环单元的径向和轴向长度，这样不仅可以减少材料的消耗节约成本，而且整个水轮发电机机组转动部分的重量减小，系统的有效承载能力也能得到提高;(2)增加永磁环间轴向气隙长度，这样安装难度也得到减小。

由于主轴直径不能改变，因而静、动永磁体内径要固定不变。

由2.3 节可以看出，承载力大小受永磁体环轴向长度变化最大，径向长度次之，气隙长度最弱。因而尝试先从减小永磁体环轴向长度开始进行，而为了充分利用永磁体磁性，永磁体环径向长度需小于轴向长度。最后，改变气隙长度大小对承载力进行微调。改变尺寸参数进行多次有限元建模计算尝试，得到参数调整后一组可供选择的尺寸参数与原永磁悬浮装置对比如表2 所示。

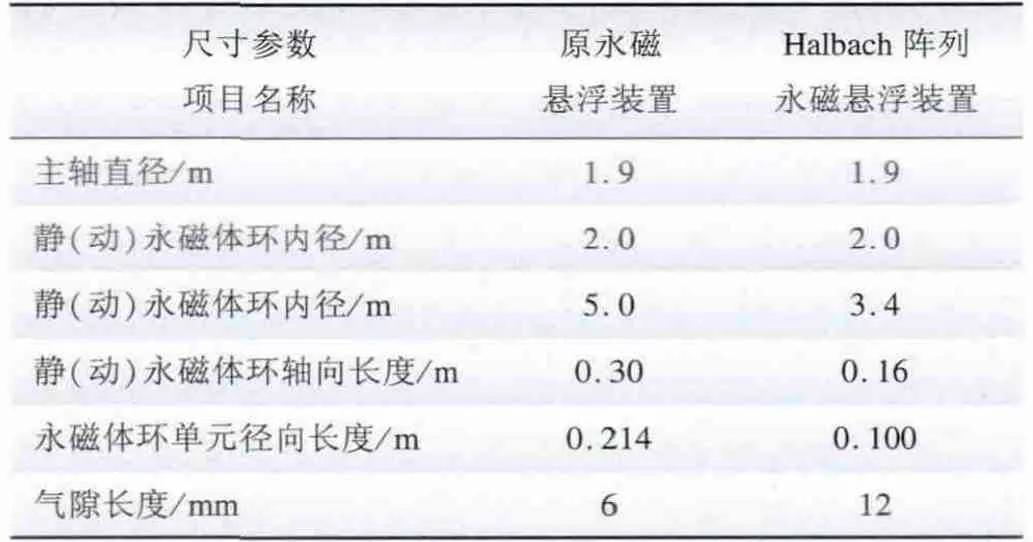
表2 调整后Halbach 阵列永磁悬浮装置尺寸与原永磁悬浮装置对比Tab．2 Size comparison between permanent magnetic levitation device with Halbach array after adjustment and original device

尺寸参数调整后的Halbach 阵列永磁悬浮装置承载力分布矢量图如图9 所示。表2 所示Halbach 阵列永磁悬浮装置在设计尺寸下能提供的承载力为548.8 t，达到了设计要求。由此可见，整个装置体积得到很大程度的减小，材料和成本也得到了有效节约。

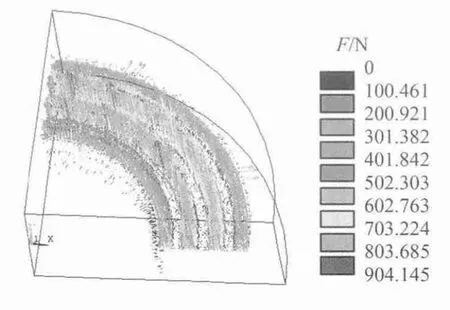
图9 尺寸参数调整后承载力分布矢量图Fig.9 Vector distribution of bearing force after structure parameters adjustment

3 结 论

(1)将Halbach 阵列应用到基于水轮发电机组的混合磁悬浮承重系统中的永磁装置中，极大地提高了所能提供的承载力水平，从而装置尺寸可以得到适当减小以降低对占用空间的需求。

(2)永磁悬浮装置提供的承载力与永磁体环间气隙长度基本成反比，与永磁体环径向长度基本成正比，随永磁体环的相对磁导率增大而减小，随永磁体环轴向长度增大而增大。

［1］程云山．水泵水轮机弹性盘支承推力轴承烧损事故分析及处理［J］．水利水电科技进展，2007，27(5):59-61．

［2］王斌．混合磁悬浮水轮发电机转子系统承重研究［D］．南京:河海大学，2009．

［3］马宏忠，王斌，鞠平．混合磁悬浮水轮发电机组转子系统设计与建模［J］．河海大学学报:自然科学版，2010，38(3):342-346．

［4］马宏忠，王斌，鞠平．混合磁悬浮水轮发电机组转子承重系统可行性分析［J］．河海大学学报:自然科学版，2010，38(4):467-471．

［5］黄学良，周赣，张前．平面电机的Halbach 型直线电机执行器［J］．中国电机工程学报，2009，29(27):80-86．

［6］Jae S C，Jeonghoon Y． Design of a Halbach magnet array based on optimization techniques［J］． IEEE Transaction on Magnetics，2008，44(10):2361-2366．

［7］江大川，刘淑琴，虞烈，等．电磁推力支承系统结构参数设计的研究［J］．西安交通大学学报，1997，31(12):17-22．

［8］冯慈璋，马西奎．工程电磁场导论［M］． 北京:高等教育出版社，2000:151-152．

［9］盛剑霓．电磁场数值分析［M］．北京:科学出版社，1984:66-68．

［10］孙明礼，胡仁喜，崔海蓉，等． ANSYS 10.0 电磁学有限元分析实例指导教程［M］．北京:机械工业出版社，2007:18-36．

［11］Jiang H，Huang X L，Huang X Q．Calculation and analysis of the 3D magnetic field of Halbach PM array based on equivalent magnetic charge method ［C］//Proceedings of the 11th International Conference on Electrical Machines and Systems． Wuhan:IEEE，2008:368-372．

［12］Rovers J M M，Jansen J M，Lomonova E A．Caculation of the static forces among the permanent magnets in a Halbach array［J］． IEEE Transaction on Magnetics，2009，45(10):4372-4375．

［13］徐飞鹏，李铁才．采用Halbach 磁场的新型被动磁轴承仿真［J］．电机与控制学报，2007，11(5):538-541．

［14］李春生，杜玉梅，夏平畴，等． 磁浮列车工程中的Halbach 永久磁铁结构的优化［J］．工程设计学报，2007，14(4):334-337．

［15］蒋浩，周赣，黄学良．基于磁荷法的环形Halbach 永磁阵列三维磁场计算［J］．微特电机，2010，1(9):1-3．

［16］陈君辉，杨逢瑜，杨龙，等．一种Halbach 阵列永磁轴承的磁力模型研究［J］．哈尔滨理工大学学报，2011，16(5):72-75．