基于复杂网络理论的城市轨道交通网络结构特性
李 朴 武子晗
(1.中铁工程设计咨询集团有限公司城市轨道交通设计研究院 北京100055;2.北京航空航天大学新媒体艺术与设计学院 北京100191)
城市轨道交通在城市公共交通系统中处于骨干地位,其大运量、高效率的特性已被广泛认可,并已经成为许多城市解决交通拥堵问题的首选方案。以北京、上海、广州为代表的特大型城市,其轨道交通正处于集中发展阶段,已经由单线运营进入网络化阶段。轨道交通网络化提高了城市轨道交通运营效率,提升了乘客出行的方便性、可达性,但同时也带来了新的问题和挑战,如单线风险的线间传递、网络客流拥堵蝴蝶效应等。而网络结构是网络特性的基础,因此需要从整体角度、网络层面对城市轨道交通网络结构特性进行研究。
图论和复杂网络理论已经广泛应用于计算机、电力和交通等各个领域,图论能将研究对象简化成直观的形式,复杂网络能描述系统的演化机制、演化规律和整体行为[1]。笔者尝试引入图论方法,并运用复杂网络的方法对城市轨道交通网络结构特性进行分析,并建立评价模型。
1 图论和复杂网络理论简述
图论起源于一个实际问题——柯尼斯堡七桥问题,1736年瑞典数学家欧拉解决了这个问题,由此图论诞生。按照数学的方法,“图”被定义为有限非空节点集合与节点无序偶集合[2]。图论中的图是由若干给定的点及连接两点的线所构成的图形。按照图论的方法,能将所需要研究的问题简化成节点和边连接的图形,将事物或研究对象之间的关系简化,以便研究。
在图论中,一般设图G=(V,E),分别称V和E的值为图G的顶点数和边数。若图G的顶点数和边数都是有限集,则称G为有限图;否则称为无限图[3]。若图G中,节点之间的边有方向,即节点之间的流动有方向性,则称图G为有向图,否则称为无向图,此时节点的度有出度和入度之分。在运用图论的方法过程中,需要对研究对象进行顶点和边的构建,赋予不同的顶点和边的概念,会得到不同的模型[4]。
复杂网络理论通过对所研究对象进行度量统计,认为网络具有小世界或无标度特性,然后建立网络模型对统计性质进行分析并研究网络规律,最后预测网络行为[5-6]。复杂网络的统计指标主要有度和度的分布、聚类系数以及平均最小距离,其中通过对度和度的分布的统计并进行曲线拟合,可以判定所研究的网络是否具有复杂网络特性[7]。
城市轨道交通网络作为技术网络的一种,已经被广泛论证具有复杂网络的性质。比如,Latora等[8]对波士顿地铁网络进行了论证,认为其具有小世界特性;陈菁菁[9]、王云琴[10]等均论证了国内城市轨道交通网络的复杂特性。
2 建立城市轨道交通线网模型
2.1 城市轨道交通线网模型
基于图论基本原理,一张典型的网络由许多节点以及连接节点的边组成。节点代表所研究系统中的一个真实个体,边则代表2个真实个体之间在某种约束条件下的相互关系。城市轨道交通网络以换乘车站为基础,线路之间经由换乘关系形成某种约束,因此可以利用图论的方法,将线路简化为一个真实个体,换乘关系为真实个体之间的约束。
在城市轨道交通线网模型中,节点表示独立运行的线路,边表示独立运行线路间的直接换乘关系。即若线路A与线路B可以经由车站C直接进行换乘,则图中表示线路A与线路B的节点间有边存在,若不能直接进行换乘,则两节点之间没有边存在。
基于复杂网络理论的基本知识,在城市轨道交通线路网络模型中,可以利用度值和权值这两个概念对其进行评价。在所建立的网络模型中,度值指与本线路直接连接的线路数目,权值指每条线路所包含的换乘车站数目。
2.2 北京城市轨道交通线网模型
从北京城市轨道交通运营网络图(见图1)可以看出,北京市开通运营线路共16条,线路里程达442 km,线路从市中心敷设至郊区,基本形成了城市轨道交通网络。根据2.1节线路网络模型构建原则,依据地铁运营网络图,可以构建如图2所示的线网模型。
2.3 上海城市轨道交通线网模型
由最新上海城市轨道交通运营线路图(见图3)可知,上海市开通运营线路共13条,运营里程达468 km,是目前中国运营线路最长的城市轨道交通系统,已经形成较为复杂的轨道交通网络。
上海地铁10号线与11号线均由主线和支线构成,且主线和支线共线运营,换乘车站主体相同,因此在构建上海城市轨道交通线网模型时,将主线和支线合并为一条线路进行建模,如图4所示。
2.4 广州城市轨道交通线网模型
由广州地铁运营线路图(见图5)可知,广州地铁开通运营线路共9条。其中3号线北延段从体育西路站起独立运营,且车站数目较多,因此在建立广州的线网模型(见图6)时,将3号线北延段作为独立节点。
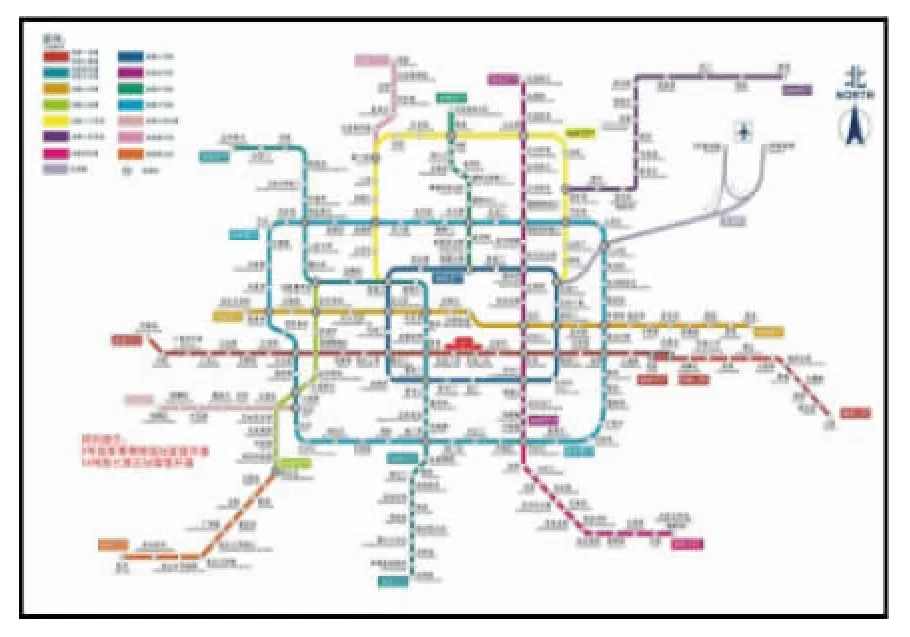
图1 北京地铁运营线网
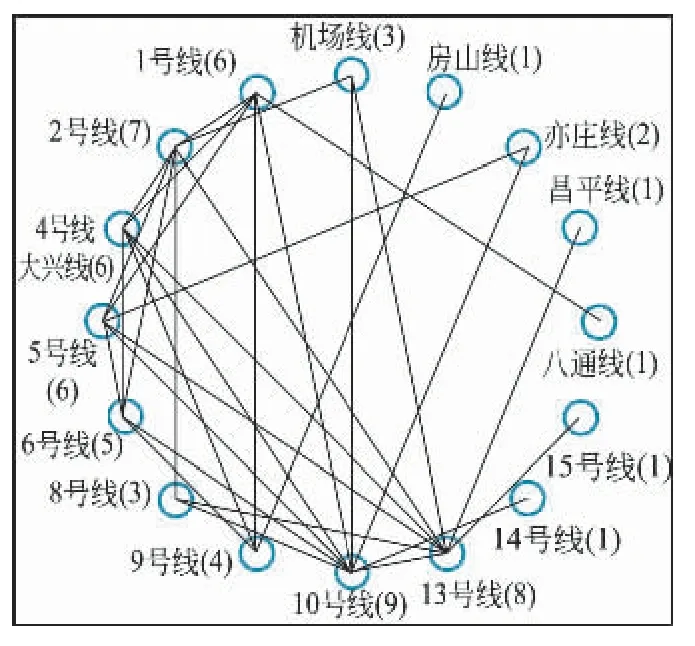
图2 北京地铁线网模型
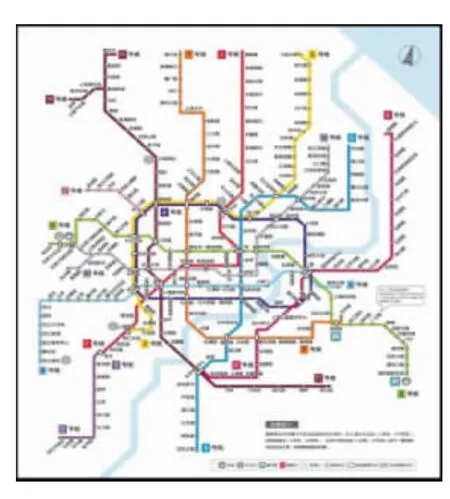
图3 上海地铁运营线网
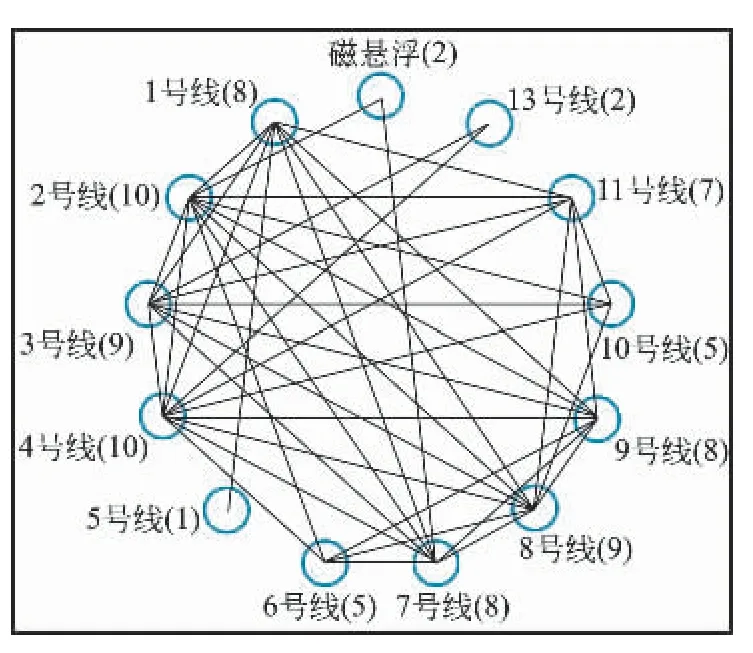
图4 上海地铁线网模型
3 城市轨道交通线网模型的复杂性
3.1 城市轨道交通网络结构特性
对所建立的线网模型,通过度值和权值的分析,可以分别得到北京、上海及广州的线网复杂特性,如表1所示。由表1可知北京地铁网络的平均度值为4,说明该网络中平均每条线路与4条线路进行连通;北京地铁网络的平均权值为4.75,说明该网络中平均每条线路拥有4.75个换乘车站。同理可以得到,上海地铁线路拥有最高的线路连通性以及换乘车站数目。

图5 广州地铁运营线网

图6 广州地铁线网模型
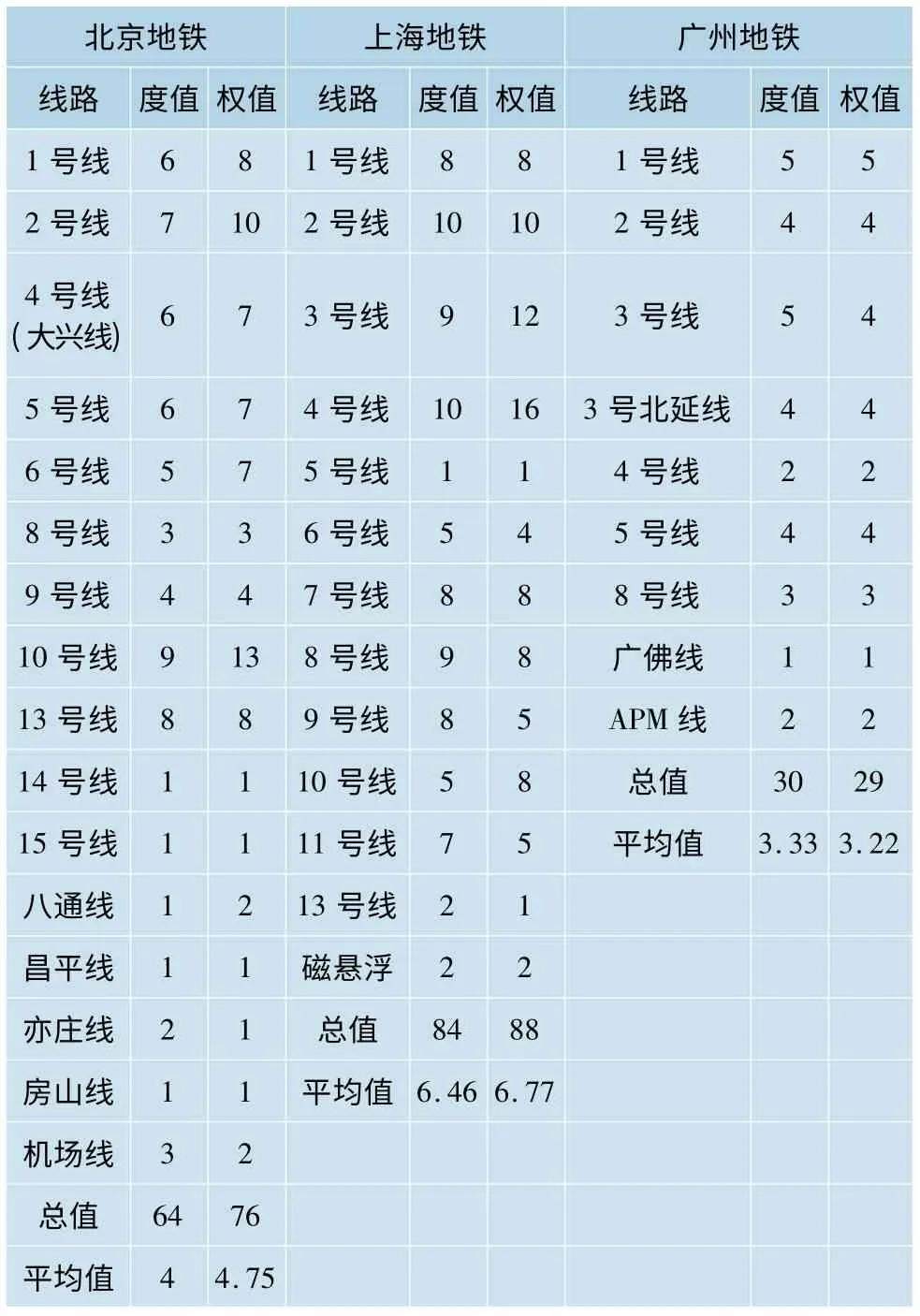
表1 城市轨道交通线网复杂特性指标统计
度值和权值作为一对指标,能够很好地反应线网的复杂特性。以北京市为例,根据本文2.2节中所建立的模型可知,北京城市轨道交通线网模型是一个由16个节点组成的拓扑结构网络。在线网模型中,通过节点之间的边可以直观地看出线路之间的连接关系,并由此得出线路间的换乘关系。如1号线节点与2、4、5、9、10以及八通线节点相连接,则表示1号线可以与这6条线直接进行换乘,由于1号线节点与6个节点相连接,因此1号线节点的度值为6。
顶点的度值分布直观地反映了轨道交通线路的可达性和连通性。从节点的度分布来看,每个节点的度值均大于1,这说明模型中所包含的线路之间均存在直接换乘关系,即互相连通。有近3节点的度值为1,说明这些线路只与其他某条线路存在换乘关系,从实际运营网络图中可以发现,这些线路均为郊区线,这些线路在网络中的连通性很低;有近一半的节点的度值大于5,说明这些线路与多条线路之间存在换乘关系,这些线路是穿越城中心的线路或者环线,这些线路在网络中的连通性较高。
3.2 城市轨道交通网络对比
不同城市的轨道交通线路会形成不同的轨道交通网络,而不同的网络又具有不同的特性。模型结果显示,广州的线路模型中节点数目最少,北京的线路模型中节点数目最多,而上海的线路模型最复杂,节点间边的数目最多。在对3个城市的轨道交通网络进行对比分析时,引入连通率的概念,以此来评价城市轨道交通网络的连通性。连通率在可靠性评价中,已经得到了广泛的应用,对于不同的系统有不同的含义,在城市轨道交通网络中,将连通率定义为:在正常运营的网络中,每条线路所连通的全部线路占整个网络线路数的平均值。城市轨道交通网络连通率P的计算公式为
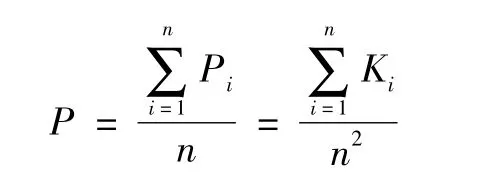
式中:Pi是线路i的连通率;Ki是网络模型中代表线路i的节点的度值,n是网络中线路的数目。
通过对网络模型的分析,利用上述公式可以计算出3个城市的轨道交通网络连通率,如表2所示。

表2 2013年网络连通率对比分析
根据表2可知,上海市轨道交通网络连通率最高,北京市轨道交通网络连通率最低,连通率与市区的线网密度成正比,其中北京市区线网密度是指北京市四环内线网密度。这说明北京市地铁运营网络的出行效率比较低,乘客经由地铁出行时的直达可达性比较低。通过对市区线网密度的统计,在北京地铁运营网络中,虽然北京市地铁运营里程较大,但是网络中郊区线占据了运营里程的较大部分,市中心区的地铁线网密度并不大,这是影响整个网络连通率不高的因素之一,所以北京市需要加大城中心区地铁线路的修建,以提高整个网络效率。
4 结语
笔者引入图论的方法,建立了以运营网络为基础的城市轨道交通线网模型,并对北京、上海、广州的网络模型进行了对比分析。通过模型的建立,可以迅速确定城市轨道交通网络中线路的重要等级,可以为线路的等级划分提供理论依据。重要度等级比较高的线路,如北京地铁2号线和10号线,在资源配置时应该优先考虑,合理分配较多的人员和设备。网络连通性对比分析的结论表明,北京和广州在城市中心区域,还需要规划建设更多的线路,提高中心区线网密度,以达到整个网络高效运营的目的。
[1]吴建军,高自友,孙会君,等.城市交通系统复杂性:复杂网络方法及其应用[M].北京:科学出版社,2010:5-10.
[2]慈立坤,胡蒙达.上海城市轨道交通网络运营可靠性研究[J].城市轨道交通研究,2004(5):41-44.
[3]王海英,黄强,李传涛,等.图论算法及其MATLAB实现[M].北京:北京航空航天大学出版社,2010:1-5.
[4]马嘉琪,白雁,韩宝明.城市轨道交通线网基本单元与复杂网络性能分析[J].交通运输工程学报,2010(4):65-70.
[5]Sun H J,Wu J J.Scale-free characteristics of supply chain distribution networks[J].Modern Physics Letters:B,2006(17):841-844.
[6]孙仁诚,邵峰晶.青岛市公交线路网络复杂性分析[J].复杂系统与复杂性科学,2009(9):63-68.
[7]刘志谦,宋瑞.基于复杂网络理论的广州轨道交通网络可靠性研究[J].交通运输系统工程与信息,2010(10):194-200.
[8]Latora V,Marchiori M.Is the Boston subway a smallworld network?[J].Physica:A,2002,314:109-113.
[9]陈菁菁.基于复杂网络的城市轨道交通网络可靠性研究[J].都市快轨交通,2010,23(2):18-21.
[10]王云琴.基于复杂网络理论的城市轨道交通网络连通可靠性研究[D].北京:北京交通大学,2008.

