基于方差分量估计的高精度工业测量自由设站*

周跃寅 潘国荣 郭 巍

(同济大学测绘与地理信息学院，上海 200092)

1 引言

测量数据处理中，要获得最优的参数估计，除需要建立正确的数学模型外，合理的随机模型也是不可或缺的。方差分量估计理论出现之前，人们通常采用根据观测值的先验精度定权方法来确定观测值的方差协方差阵，进而建立其随机模型，但实践证明这种方法在很多情况下不够精确。20世纪70年代之后逐渐出现了各种用验后的方法估计各类观测值的方差，并由此定权［1－13］。

在实际应用中，由于采集的数据量有限，利用各种方差分量估计的算法来推算观测值方差都只能是近似的逼近，但多余观测数越少，近似效果越差，甚至出现估计出的方差或协方差为负的情况。为解决这类问题，文献［12］提出了在极大似然VCE 模型中附加协方差阵的非负定约束条件，文献［13］提出了在最小二乘VCE 模型中附加协方差阵的非负定约束条件。文献［14］将方差分量估计引入正则化解法中，用于解决线性反演中观测权阵未知的情况。

本文将方差分量估计应用到高精度工业测量中，用以解决通过自由设站求解测站三维坐标问题，通过大量实验数据总结了方差分量估计在工业测量自由设站解算中的应用规律，研究了多余观测数的多寡对于方差分量估计对空间自由设站的影响。

2 方差分量估计

以间接平差为例，设L 为观测值向量，其权阵为P，X 为待定参数，A 为观测系数阵，则误差方程

若观测值可分为m 类，且观测值之间相互独立，则:

法方程为:

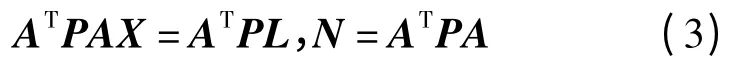
对应m 类观测值:

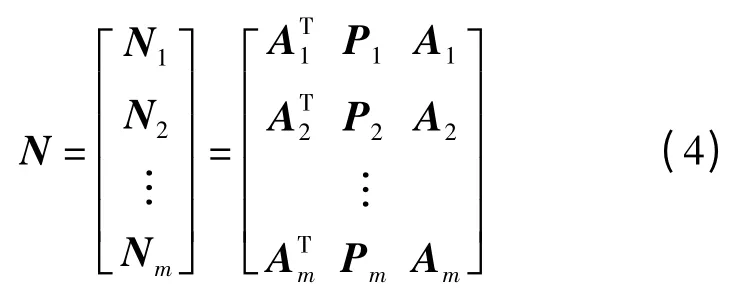
其中，a=N－1N

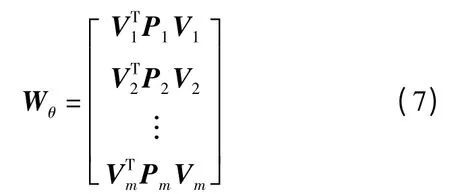
其中，n1，n2，…，nm为各类观测值的个数，为求得的各类观测值的单位权方差。在方差分量估计解算中，第一次解算的各观测值单位权方差并不相同，需要迭代运算，不断重新定权:

3 工业测量空间自由设站

工业测量空间自由设站是通过测量仪器测量出测站点到n 个已知点的斜距、水平角和竖直角，来反求出测站点在已知坐标系统中的三维坐标。设要求解的测站点坐标为，各观测的已知点坐标为(XiYiZi)T，i=1，2，…，n。三类误差模型

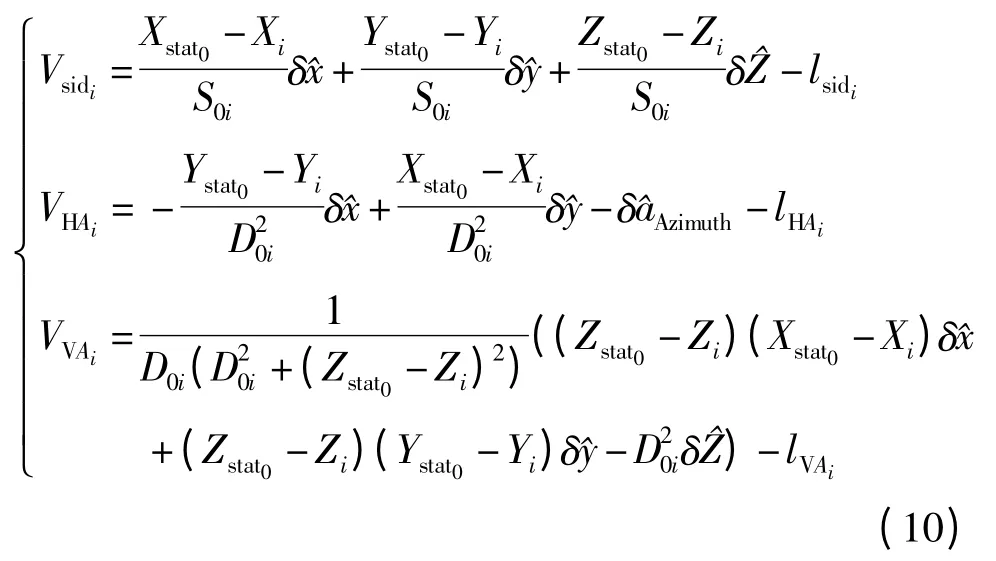
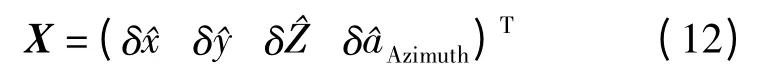
利用式(12)的改正数，加上此次运算的各参数初值作为下次迭代的初值，不断迭代至上述改正数小于某一足够小的常量为止，则认为解算结束，返回求解的测站坐标及初始零方向方位角，同时利用式(5)求得此次各类观测值的单位权中误差。

4 实验数据

4.1 取7 个已知点进行方差分量估计定权

以空间自由设站定测站坐标为例，使用跟踪仪观测了已知坐标系中的7 个点，同时获取了7 个斜距观测值、水平角观测值和竖直角观测值(表1)。

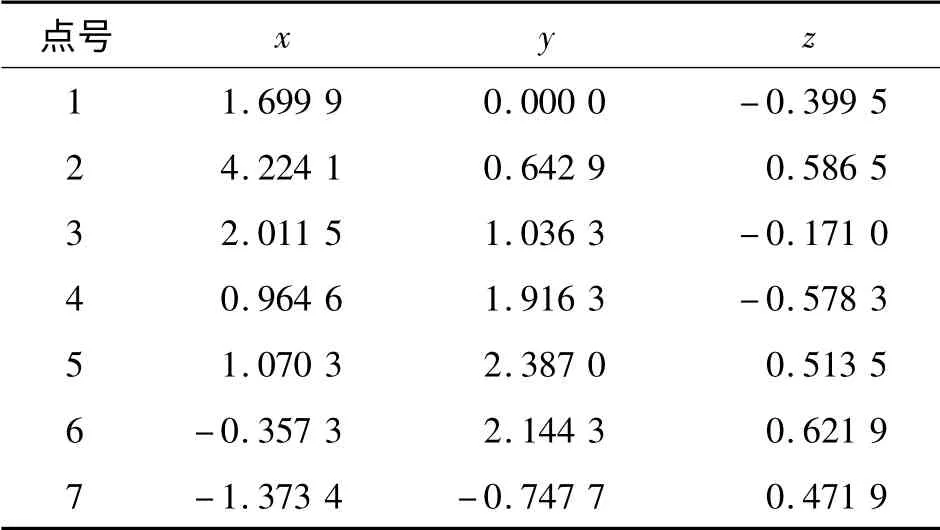
表1 已知坐标系的7 个三维坐标点(单位:m)Tab.1 7 Coordinate points in 3-dimention(unit:m)

如果给定测站点的坐标，可以精确地模拟解算出测站点到各已知点的斜距、水平角和竖直角，再加上各类观测值应有的服从正态分布的误差，即可模拟现实中的观测量，假定给定的该坐标系下测站点坐标如表2。

表2 假定测站点精确坐标(单位:m)Tab.2 Accurate coordinate of assumed station(unit:m)

已知某跟踪仪在10 m 内标称的测距精度为15 μm，测角精度为0.5″，那么可以模拟出测距误差Δsid～N(0，(15 μm)2)，水平角和竖直角在半测回的观测误差Δdir～N(0，(0.7″)2)，通过解算出的观测值加上上述的误差得到一组模拟观测值如表3。

表3 模拟观测值Tab.3 Simulated observation values

如果将原始观测值中的斜距作为一类观测值，水平角和竖直角归为另一类观测值，由式(5)估计出这两个单位权方差分别表示为和，并不断迭代至各单位权方差近似相等为止，单位权方差的迭代过程计算如表4。

表4 单位权方差迭代过程(单位:s2)Tab.4 Interative process of unit weight variance(unit:s2)

图1(a)为1 000 次实验中估计的测距中误差，图1(b)为1 000 次实验中估计的测角中误差，图2为以测距中误差作为x轴，测角中误差作为y轴的1 000次实验的散点图，具体的统计数据如表5。

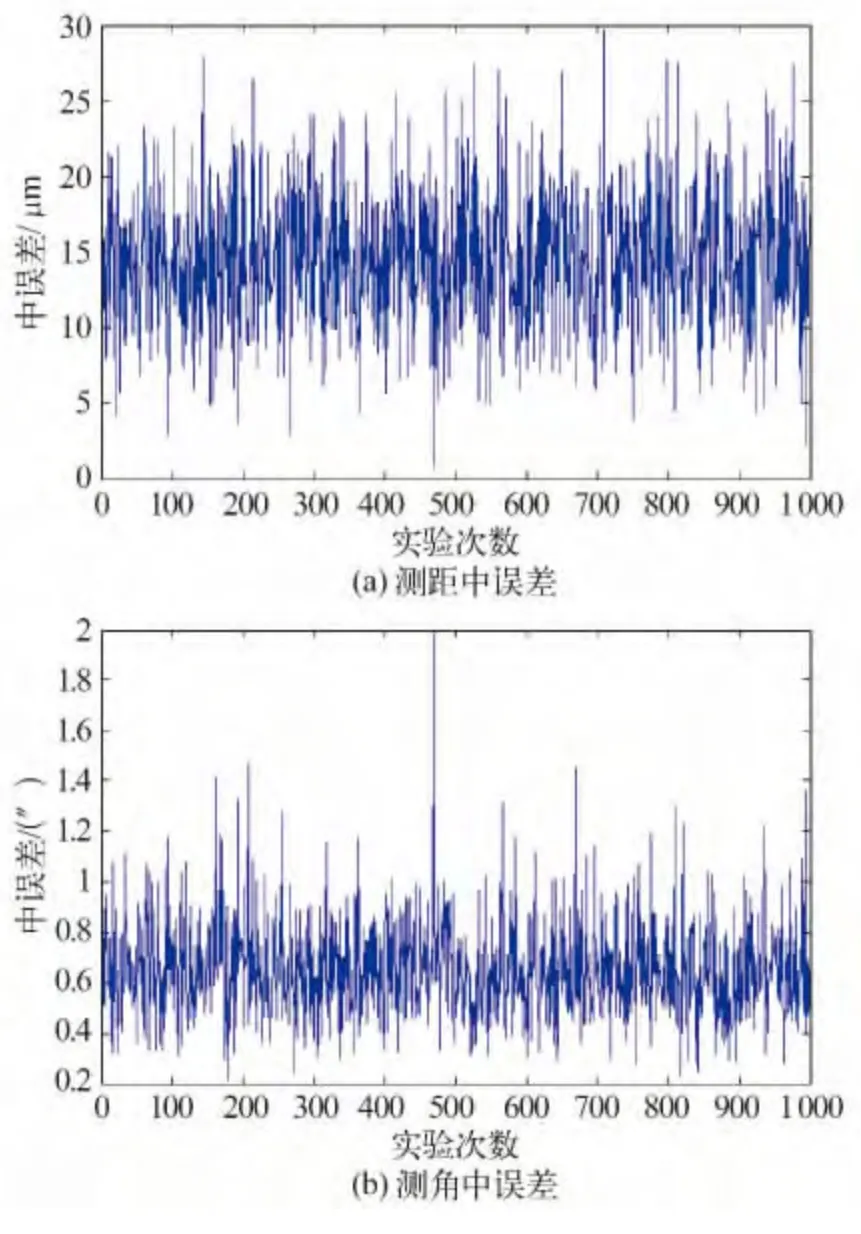
图1 单位权中误差统计图Fig.1 Statistical graph of calculating unit weight mean error

这1 000 次解算出的测站坐标与平均值的偏差如图3。

从图3 可以看出各向偏差基本都在15 μm 以内。三个方向上的测站坐标标准中误差如表6。

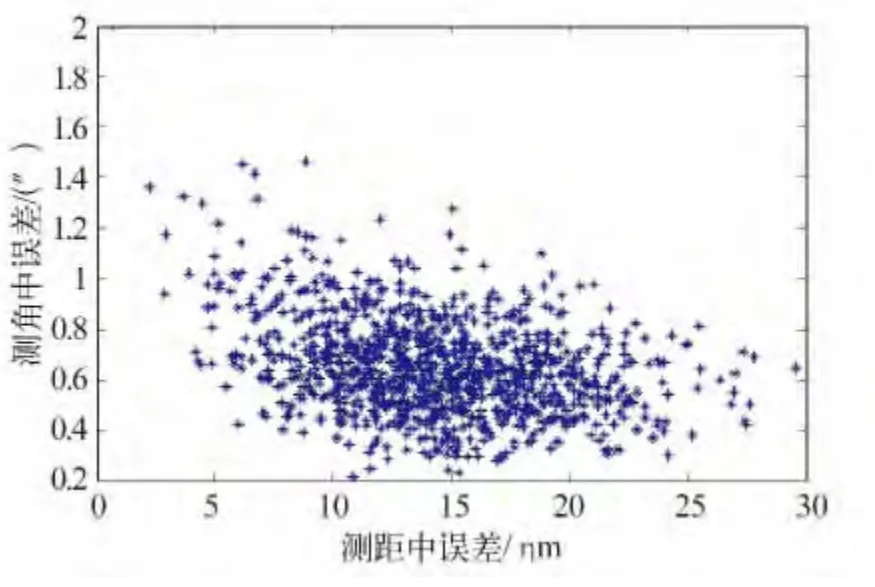
图2 单位权中误差散点图Fig.2 Scatter diagram of calculating unit weight mean error

表5 1 000 次方差估计解算结果Tab.5 Calculated results of variance for 1000 experiments

表6 1 000 次解算测站坐标各向标准中误差(单位:μm)Tab.6 Standard error of each direction in calculating station coordinate for 1 000 experiments(unit:μm)

4.2 选取4 个点进行方差分量估计定权

为了进一步验证多余观测量对于方差估计的影响，模拟仅仅观测其中4 个点，以同样的步骤进行1 000次实验，得到的结果如图4、图5。

可以看到估计出的测距中误差和测角中误差的范围都比7 个点的数据要大，对比图5 和图2，可以看出测距中误差比测角中误差更加离散，具体统计数据如表7。

对比表5 和表6 可以看到方差分量估计出的测距中误差和测角中误差在多余观测数少的情况下越发不稳定，而且测距中误差的不稳定性更明显，造成这个结果的主要原因是因为在工业测量自由设站中，测角的观测值是测距观测值的两倍，相同观测点的情况下测角的多余观测值始终比测距的多余观测值多，但是平均的测距中误差和测角中误差变化不是很大，比较接近设定的原始数据，而且平均的测站坐标都与原始给定的设计坐标在μm级上相同。同样可以得到这1 000 次解算的测站坐标与平均值的偏差如图6。

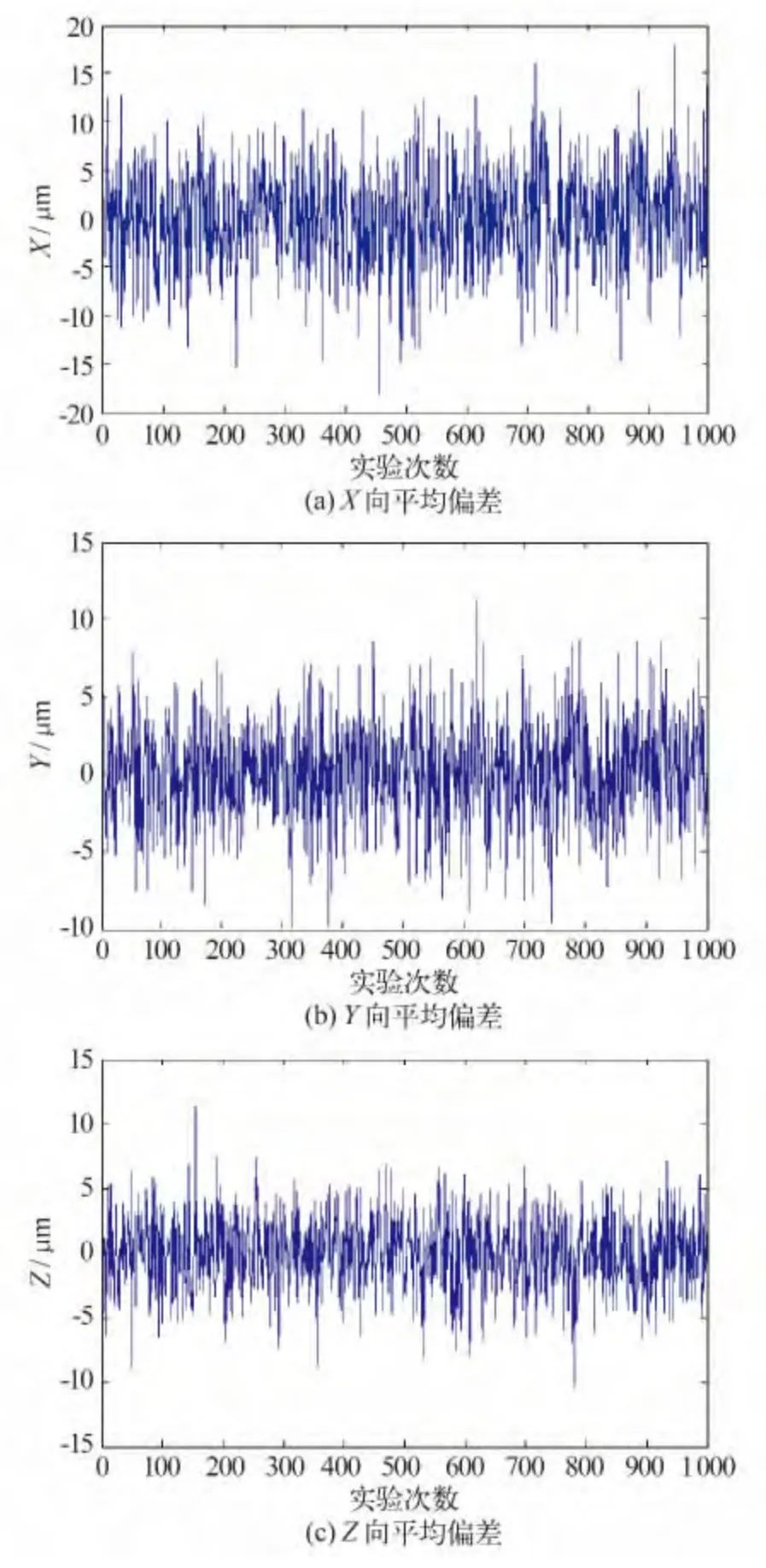
图3 测站坐标偏差Fig.3 Deviation of station coordinate

表7 1 000 次方差估计解算结果Tab.7 Calculated results of variance with 1 000 experiments

由图6 可知，测站坐标与平均值的各向偏差最大可达到90 μm，远大于图3 中7 个点解算的结果，此时三个方向上的测站坐标标准中误差如表8。

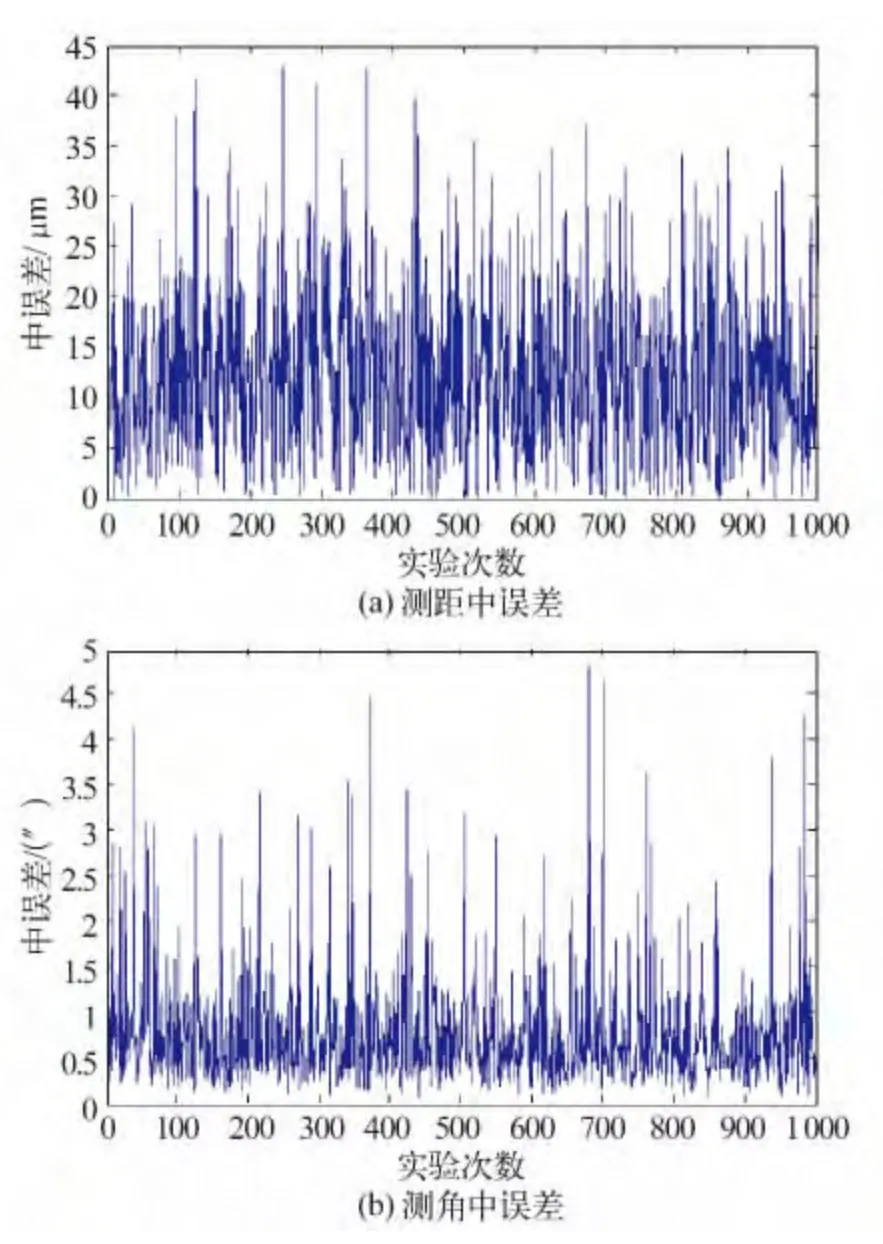
图4 单位权中误差统计Fig.4 Statistical graph of calculating unit weight mean error

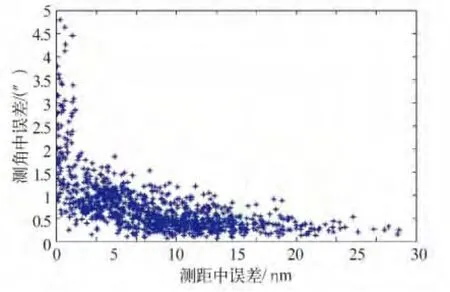
图5 单位权中误差散点图Fig.5 Scatter diagram of calculating unit weight mean error

表8 测站坐标各向标准中误差(单位:μm)Tab.8 Standard error of each direction in calculating station coordinate(unit:μm)

4.3 采用传统先验精度定权解算

在传统解算中，一般使用的仪器先验精度进行定权，但是如果仪器实际的测量精度与标称精度并不吻合，就会造成在平差时的随机模型不准确，为了对比研究其差异性，仍然使用含有相同误差精度的原始观测值，即Δsid～N(0，(15 μm)2)，Δdir～N(0，(0.7″)2)，使用同样观测的4 个已知点，而在定权时采取不同的先验精度定权，比如以测距中误差3 μm测角中误差3.5″来进行定权，得到1 000 次解算的测站坐标与平均值的偏差如图7。三个方向上的测站坐标标准中误差如表9。

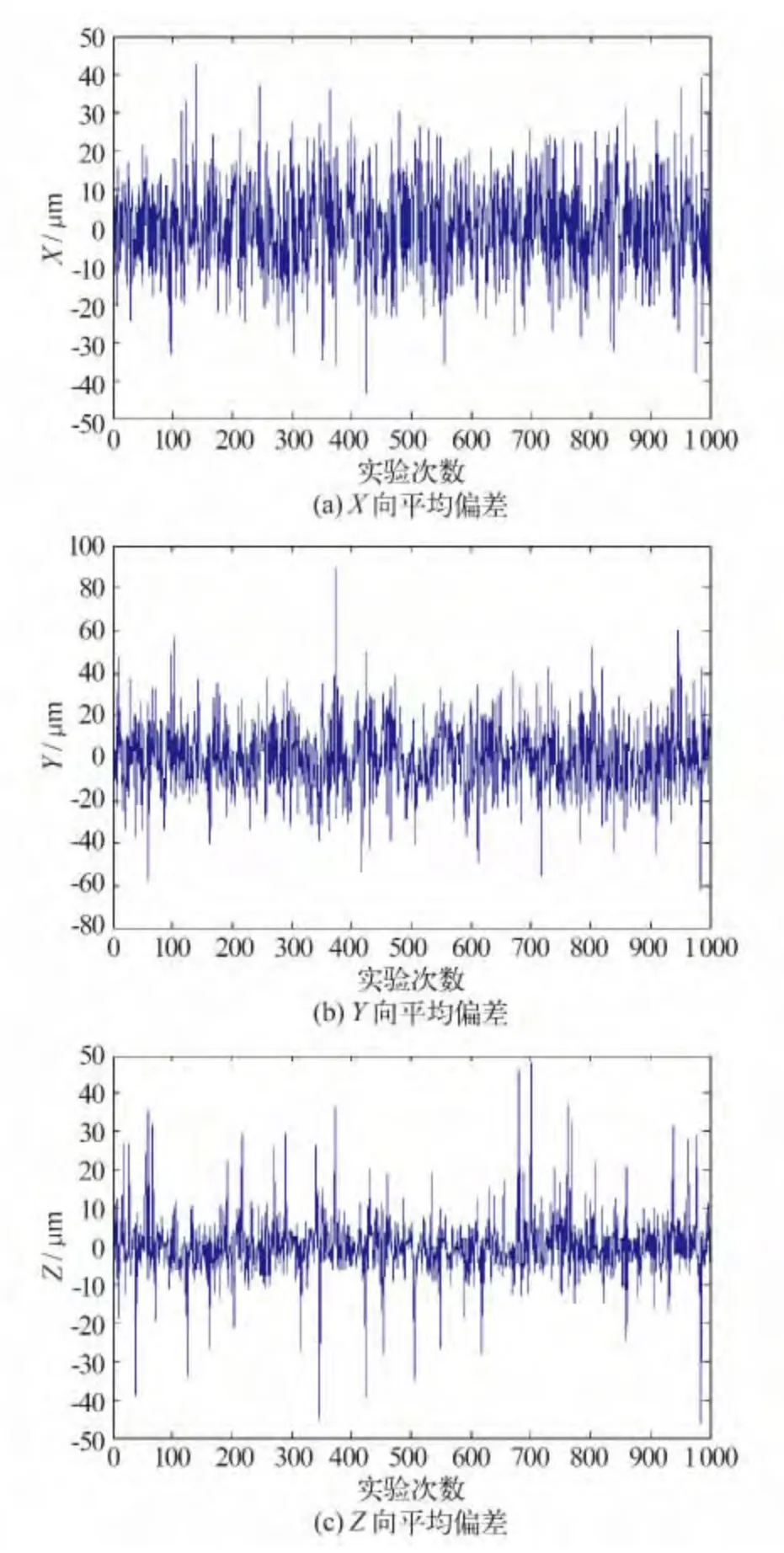
图6 测站坐标偏差Fig.6 Deviation of station coordinate

表9 不准确先验权解算测站坐标各向标准中误差(单位:μm)Tab.9 Standard error of each direction station coordinate calculated with inaccurate prior weight(unit:μm)

虽然与之前的实验数据对比，在1 000 次解算的测站坐标均值仍然在μm级别上同原始设计坐标相同，但显然较表8 中解算的测站标准中误差要大，即在特定的一次解算中测站坐标的可靠性要低。

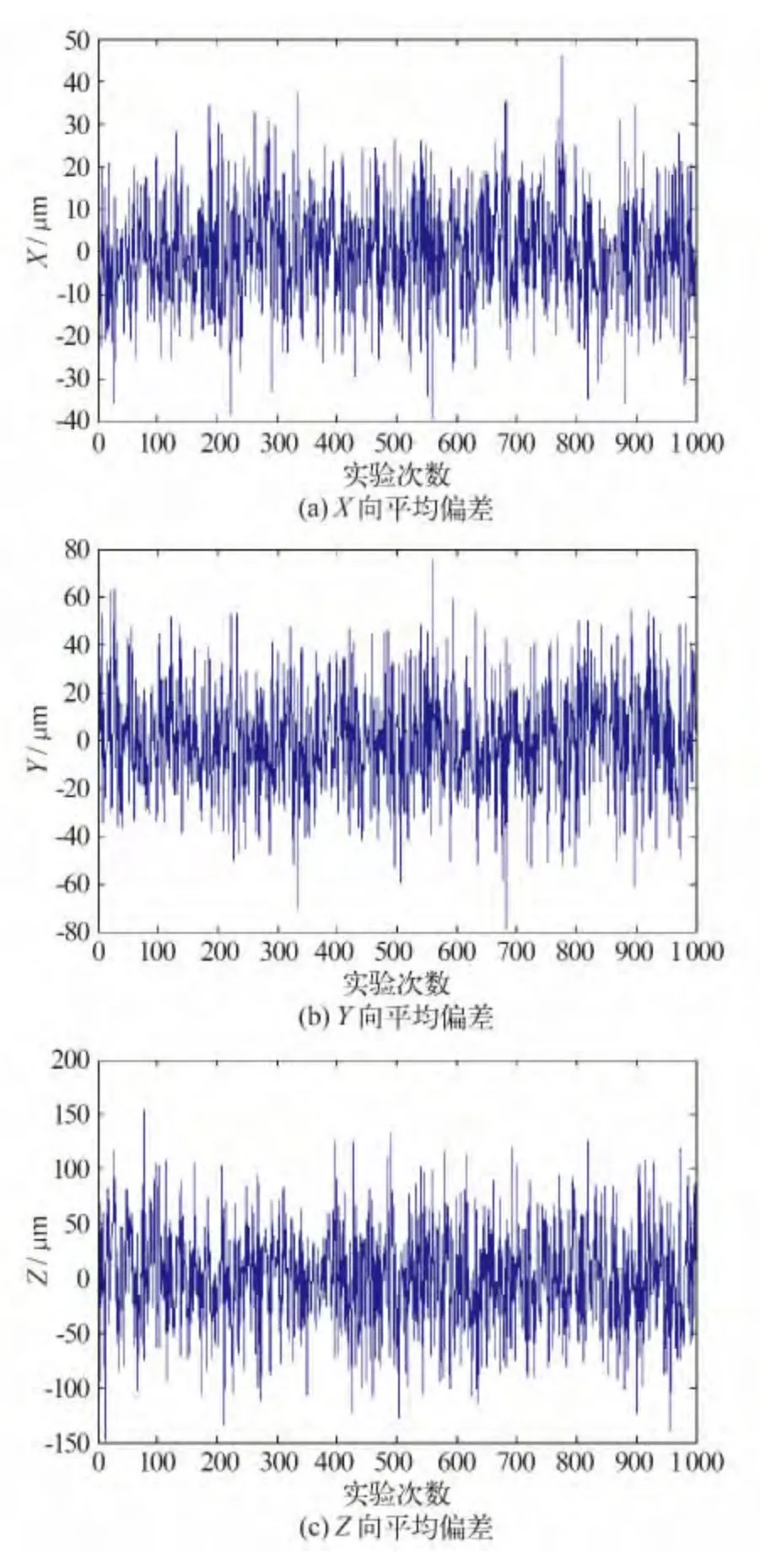
图7 不准确先验权解算结果偏差Fig.7 Deviation of calculated station coordinate with inaccurate prior weight

5 结论

1)方差分量估计的结果在一次解算中会受到有限观测数据的影响而具有随机性，多余观测数越少则估计的结果越离散，但估计的各类中误差的期望一般比较稳定;

2)在高精度工业测量自由设站中，将原始观测值分成两类的情况下，减少观测的已知点个数，测边中误差受其影响的离散程度比测角中误差大，由于测角的多余观测比测边的多，更进一步证实了多余观测数越多，方差分量估计的结果越稳定;

3)在高精度工业测量自由设站解算中，各类观测值定权的准确与否严重影响着最终参数评定的可靠性;

4)采用方差分量估计定权在处理含有多类观测值的平差问题时，估计的各观测值精度与实际测量精度是吻合的，因而相比传统的方法所采用的仪器标称精度定权更合理。

1 崔希璋，等.广义测量平差(2 版)［M］.武汉:武汉大学出版社，2009.(Cui Xizhang，et al.Generalized surveying adjustment(2nded)［M］.Wuhan:Wuhan University Press，2009)

2 Rao C.Linear statistical inference and its application［M］.John Wiley，New York，1973.

3 Rao C.Estimation of variance and covariance componentsminque theory［J］.Journal of Multivariate Analysis，1971，(1):257－275.

4 Koch K R.Parameters chaetung und Hypothesentests in Linearen Modellen［M］.Bonn:D mmlers，1980.

5 Koch K R.Maximum likelihood estimate of variance components［J］.Bull Geod.，1986，60:329－338.

6 李德仁，袁修孝.误差处理与可靠性理论［M］.武汉:武汉大学出版社，2002.(Li Deren and Yuan Xiuxiao.Error processing and reliability theory［M］.Wuhan:Wuhan University Press，2002)

7 秦显平，杨元喜.抗差方差分量估计在卫星定轨中的应用［J］.大地测量与地球动力学，2003，(4):40－43.(Qin Xianping and Yang Yuanxi.Application of robust variance component estimation to satellite orbit determination［J］.Journal of Geodesy and Geodynamics，2003，(4):40－43)

8 何海波，杨元喜.GPS 观测值先验方差-协方差阵实时估计［J］.测绘学报，2001，30(1):42－47.(He Haibo and Yang Yuanxi.Real－time estimation of a prior variance－covariance for GPS observation［J］.Acta Geodaetica et Cartographica Sinica，2001，30(1):42－47)

9 郭海荣，等.导航卫星原子钟Kalman 滤波中噪声方差-协方差的确定［J］.测绘学报，2010，39(2):146－150.(Guo Hairong，et al.Determination of convariance matrix of Kalman filter used for time prediction of atomic clocks of navigation satellites［J］.Acta Geodaetica et Cartographica Sinica，2010，39(2):146－150)

10 童小华，赵建国.GIS 中地籍宗地面积的方差分量估计［J］.测绘学报，2002，(5):109－112.(Tong Xiaohua and Zhao Jianguo.Variance component estimation of cadastral parcel area processing in GIS［J］.Acta Geodaetica et Cartographica Sinica，2002，(5):109－112)

11 杨元喜，张菊清，张亮.基于方差分量估计的拟合推估及其在GIS 误差纠正的应用［J］.测绘学报，2008，37(2):152－157.(Yang Yuanxi，Zhang Juqing and Zhang Liang.Variance-covariance component dstimation based collocation and its application in GIS error fitting［J］.Acta Geodaetica et Cartographica Sinica，2008，37(2):152－157)

12 Xu Peiliang，et al.Estimability analysis of variance and covariance components［J］.Journal of Geodesy，2007，81:593－602.

13 李博峰，沈云中，楼立志.基于等效残差的方差-协方差分量估计［J］.测绘学报，2010，39(4):349－354.(Li Bofeng，Shen Yunzhong and Lou Lizhi.Variance-covariance component estimation based on the equivalent residuals［J］.Acta Geodaetica et Cartographica Sinica，2010，39(4):349－354)

14 Xu Peiliang，et al.Variance component estimation in linear inverse Ⅲ-posed models［J］.Journal of Geodesy，2006，80(2):69－81.