盾构通用管片排版与纠偏控制的简化解算*
潘国荣 荣一夫
(同济大学测绘与地理信息学院,上海 200092)
1 引言
通用管片又称“通用楔形管片”,隧道全部采用楔形管片。通过管片的旋转组合可以拟合隧道轴线的变化,而使用通用管片的盾构掘进时能通过选择不同的拼装点位来拟合设计轴线,因此近年来通用管片的使用越来越受到重视。
本文通过对管片选型的现状分析,建立了一种结合隧道设计轴线、盾构机轴线、管片成型轴线的简化管片选型方法,并将该方法用于某地铁区间的施工过程,结果证明该方法可以有效的提高排版效率并简化计算过程,同时偏差控制在允许范围内。
2 通用管片的排版和纠偏
2.1 三轴线简化解算
将三维空间简化为平面和垂直两个独立的平面,用当前盾构机的姿态,管片姿态和设计轴线数据进行管片选型[1]。管片选型前,需要考虑盾尾间隙、已施工隧道中心线与设计中心线等基本参数,这些参数主要有:管片设计轴线与设计轴线夹角α,α=arctan[(B2-B1)/h];设计轴线与盾构机轴线夹角β,β=arcsin[(A1-A2)/L];设计轴线与管片成型轴线的夹角θ,θ=α+β。
在施工中,纠偏情况一般分为三种[2]:偏差小于5 cm、偏差在5 ~10 cm、偏差大于10 cm。本文针对偏差在5 ~10 cm 的情形,在施工中通过设计纠偏线路来拟合设计轴线。
2.2 纠偏线路设计简化模型
实际施工路线及设计轴线都是在三维的坐标系统中,如果在三维情况下考虑曲线纠偏将加大纠偏难度。本文利用管片成型轴线和隧道设计轴线的夹角进行纠偏曲线的设计,得到一种简化模型[3]。该简化方式是将设计轴线简化为一直线,根据成形管片的夹角趋势进行线路的设计。然后根据该曲线段是处于直线段,还是缓和曲线段或圆曲线段进行进一步判断,得到实际的管片超前量和纠偏环数。
该纠偏曲线设计的简化方法为两种:一是利用投影曲线将设计轴线拆分为平面线形和纵面线形,独立考虑纠偏方式,此种方法在施工中得到有效应用;二是通过计算得到的纠偏曲线半径,可以得到管片的超前量设计值,然后根据该超前量选择合适的拼装点位,在排除施工误差的情况下,可以在较短距离内完成曲线纠偏的任务,保证施工效率[4-6]。
两种纠偏线路简化模型为:
1)管片成型轴线和设计轴线成小夹角(0 <θ <90°)
如图1 所示,此时盾构机的推进姿态朝向设计轴线,此时只需设计一圆曲线的纠偏曲线对轴线进行纠正,纠偏曲线的终点即为圆曲线的切点,取δ 为设计轴线与管片成型轴线的偏差,即5 cm <δ <10 cm,L'为纠偏的范围,由于δ 偏差较小,相对于L'小的多,近似有L'=L,于是可以得到纠偏曲线的半径为:
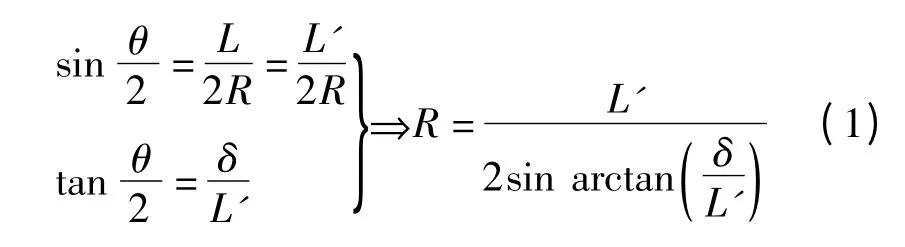
以偏差为50 mm 为例,每环纠偏量控制在5 mm/环。则最少需要纠偏环数为10 环,此时纠偏范围为12 m,通过式(1)可以得到纠偏半径R=12/2sinarctan(0.05/12)=1 440 m。则平均每环的超前量为

式中r 为管片的环半径,W 为管片环宽。计算得:Δ=6.2 ×1 200/1 440=5.17 mm。
通过式(2)可以计算出在不同的半径曲线下,平均每环管片所需的超前量,再根据所需的设计轴线的超前量之和,求出所需的管片组合。同时根据纠偏缓和平稳的原则,每环的纠偏控制在2 ~5 mm,则对于5 ~10 cm 的偏差,其所需的纠偏环数最少为10 ~20 环。
对于小半径圆曲线设计轴线,应对原有的超前量进行叠加,如本区间的设计曲线半径为330 m,每环的超前量为Δ=2rW/R=6.2 ×1 200/330=22.7 mm,在偏差为50 mm 的情况下,修正后的超前量为22.7 +5.17=27.87 mm。将设计轴线拆分为直线段,利用弧形纠偏曲线进行拟合,并计算纠偏曲线的长度和所需的每环超前量,然后根据设计的超前量选择合适的拼装点位。
2)成型轴线与设计轴线为大夹角(90° <θ <180°)
根据三轴线关系,纠偏曲线需要设计两段连续圆弧:第一段是缓和管片成型曲线与设计轴线之间的夹角,使管片成型曲线趋向设计轴线;第二段圆弧类似于1),即成型轴线通过第一段的纠偏曲线与设计轴线成小夹角,此时通过设计第二段圆弧,使偏向设计轴线的管片成型曲线逐渐缓和过渡,相切于设计轴线,达到纠偏目的。第一段的圆曲线半径R1可自行设定,但应该大于管片能够拟合的最小半径,同时该曲率半径也要大于盾构机的最小转弯半径。图2 中的夹角θ 计算方法同上。第二段的纠偏方法类似于1),可计算得到圆曲线的半径R2。该纠偏曲线的起始于管片成型的当前点,纠偏的终点是与设计轴线相切的某点,该纠偏曲线是一条连续的曲线,是光滑的,所以斜率相同。
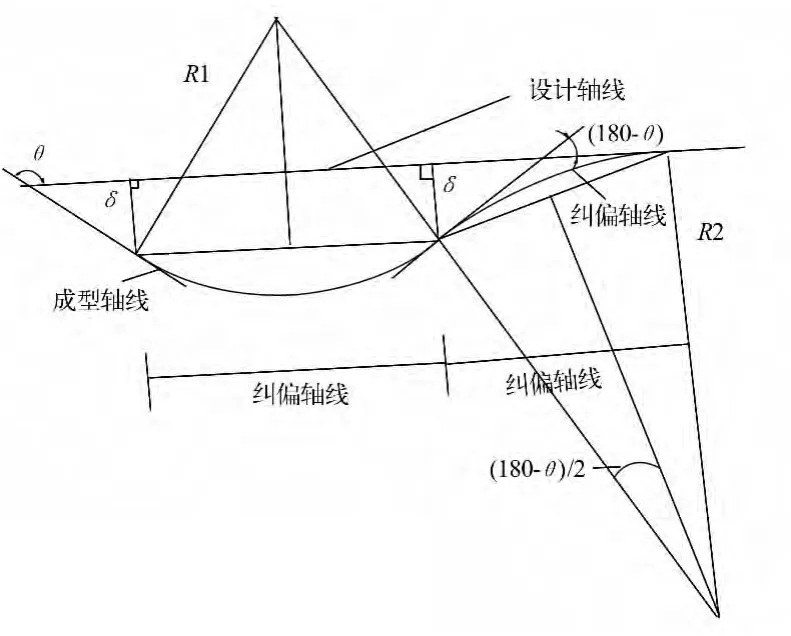
图2 成型轴线与设计轴线成大夹角Fig.2 Big angle between molding axis and design axis
施工中,管片成型曲线与隧道设计轴线的夹角很小,故此处选取夹角θ 为179°,偏差50 mm,本工程最小曲线半径为330 m,于是根据需要取第一段纠偏曲线a 的半径R1为330 m,在第一段纠偏曲线终点处的偏差同取为50 mm,此时管片成型轴线与设计轴线的夹角为1°,计算得到第一段纠偏曲线的弧长为:=11.52 m,对应于环宽为1.2 m 的管片环,需要的管片环数为:11.52/1.2=9.59,取整为10 环。
对于第二段纠偏曲线则计算方式同1),表1 取第一段纠偏曲线的半径为330 m,第二段的纠偏曲线的偏差仍为δ,即第一段纠偏曲线和第二段纠偏曲线的偏差相同,便于比较。在实际施工中,应根据此时的偏差重新计算,以得到精确的结果。
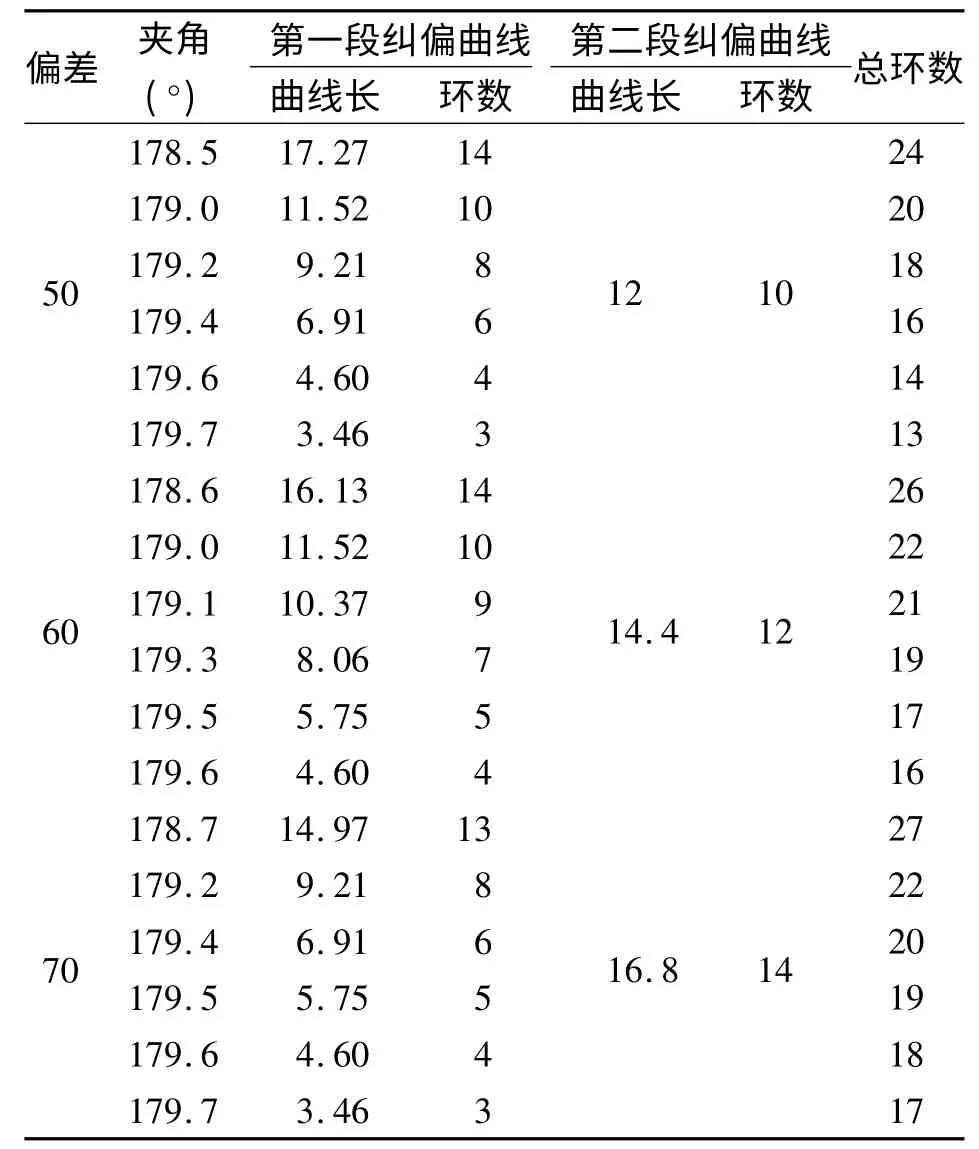
表1 成型轴线与设计轴线成大夹角纠偏情况(第一段纠偏半径为330 m)Tab.1 Correction of the big angle between molding axis and design axis
通过表1 数据可以得到微小的角度变化,也会在纠偏线路中有一定的差异,在设计中必须加入1~2 环的纠偏环,才能保证顺利过渡,使管片成型曲线趋向于设计轴线,所以要保证对于角度的精确解算,避免偏差累积造成其他影响。该角度是通过分析盾构机和管片的几何关系,利用千斤顶行程差、盾尾和切口偏差以及盾构机的参数来进行解算,所以对于这些数据应尽可能地高精度获取。
方法2)是对纠偏路线进行了简化。当盾构机偏离设计轴线,即盾构机主体趋势向外,即可使用该种方式计算,而且只要设计两段连续的弧形纠偏曲线就可以成功纠正管片成型的偏差。同时,可以根据实际情况进行半径选取,根据施工情况进行纠偏环数的调整,因此可以减少缓和曲线的应用。
以上两种简化方式,基本可以满足实际施工中发生的情况,当纠偏方向或者起始纠偏位置发生改变时,此方式依然有效。因为是在短距离内缓和平稳的纠偏,施工中可以将设计轴线看成是一直线,通过这种简化计算,可以根据纠偏的程度选择不同环数来进行纠偏,以及对纠偏距离做出调整。相对于传统的穷举法来进行纠偏设计,本模型适用于短距离的纠偏,不需考虑多种情况,就可以得到有利于施工的纠偏设计,这种简化方式针对5 ~10 cm 的偏差情况,可以得到很好的结果。但为了保证得到最优的纠偏路线,施工中还应该综合考虑盾尾间隙、盾构首尾差、油缸行程差等因素。
4 工程分析
以某地铁区间上行线为例,该区间从里程SK18+422.939 至SK18 +849.420 为一段缓和曲线和圆曲线线路,该段利用上述的方法进行了管片排版和纠偏设计,得到了排版方案,经量测得到偏差结果。
表2 为通过该方式得到的管片排版结果,通过计算纠偏路线和超前量,列出了80 环的管片选型结果,从250 环到330 环,为圆曲线的一段选型排版封顶块的设计。该设计路线为小半径圆曲线,相比于穷举法的五环或者十环纠偏的方法,计算简便,只需通过计算超前量就可以得到拼装点位,更有利于实际施工。

表2 250 ~330 环转弯环的管片排版Tab.2 Segment layout of the turning ring from 250 to 330
统计可得,通过这种设计只要在某些特殊环段改变拼装点位就可以很好地完成轴线的拟合,而且拼装方式简单,基本只在K5、K13、K7 三个拼装点位进行转换,并且能保证错缝拼装,通缝不超过两条。通过实际验证,该方式的偏差都达到了正常状态的要求,能极大的提高施工效率。
按照该拼装方式得到的偏差,分别得到了盾构机与设计轴线的偏差结果和管片成型轴线与设计轴线的偏差结果(图3、4)。
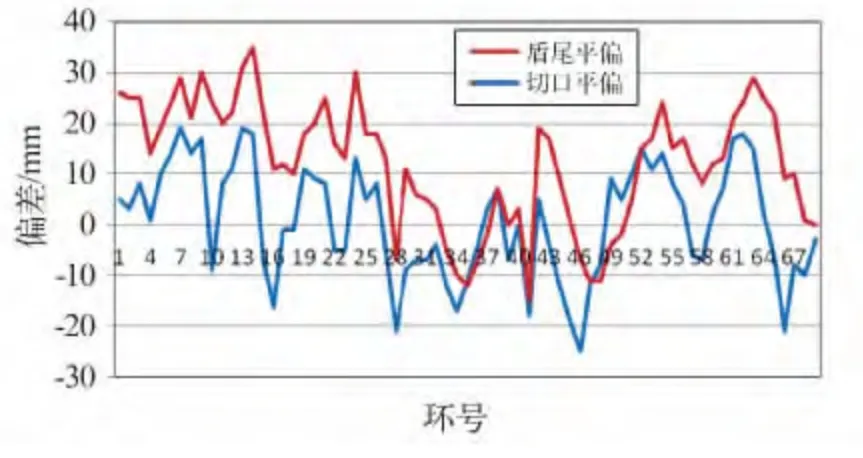
图3 盾构机与设计轴线偏差Fig.3 Deviation of shield and design axis
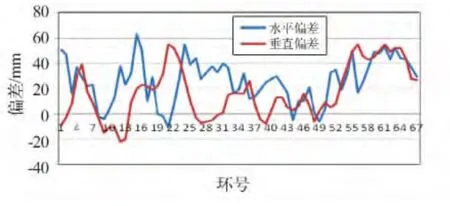
图4 管片成型轴线与设计轴线偏差Fig.4 Deviation of molding segment axis and design axis
图3、4 显示,管片成型轴线的偏差绝大多数控制在50 mm 以下,盾构机的姿态偏差也在40 mm 以下,满足该工程中偏差-100 ~100 mm 的要求。小于50 mm 的姿态一般只需调整盾构机的姿态就可以拟合设计轴线。可见在盾构施工中,通过实时的获得盾构机推进的千斤顶行程,以及盾构机的姿态差值,判断盾构机推进轴线、管片成型轴线和设计轴线三者之间的关系,预测管片环的拼装趋势,在盾构机出现偏离设计轴线5 ~10 cm 的情况中,可以合理地分析纠偏路线,保证缓和平稳的纠偏推进。这种简化的计算方式对于管片排版和纠偏有指向作用。
5 结语
通过分析设计轴线、盾构推进轴线、管片成型轴线之间的关系,根据当前管片与轴线的角度情况以及偏差情况,分析得到纠偏路线和长度、纠偏所需的管片超前量,进而得到管片的排版设计。这种方法可以快速地接近设计轴线,计算简便,可保证施工顺利进行。
1 杨群,谢立广.关于盾构隧道楔形管片环的思考[J].现代隧道技术,2010,47(3):56-59.(Yang Qun and Xie Liguang.On rings of wedge of shield tunnel segment[J].Modern Tunnel Technology,2010,47(3):56-59)
2 沈碧辉.盾构通用管片拟合排版技术应用[J].西部探矿工程,2010(3):177-179.(Shen Bihui.Application of the shield segment fitting typesetting technique[J].West-China Exploration Engineering,2010,(3):177-179)
3 朱继文,屠传豹,赖华辉.通用管片精细化施工研究思路探讨[J].低温建筑技术,2012,(11):92-94(Zhu Jiwen,Tu Chuanbao and Lai Huahui.Study on the fine construction of general segment[J].Low Temperature Architecture Technology,2012,(11):92-94)
4 刘凤华.盾构隧道通用管片拟合排版与管片选型技术研究[D].同济大学,2007.(Liu Fenghua.Study on the composition and ring selection technique of general segments for shield driven tunnels[D].Tongji University,2007)
5 李伟平,郑国平.盾构隧道通用楔形管片排版系统的核心算法研究[J].现代隧道技术,2008,(5):34-37.(Li Weiping and Zheng Guoping.Study on core algorithm of the general wedge of shield tunnel segment typesetting system[J].Modern Tunnel Technology,2008,(5):34-37)
6 刘春,等.长距离隧道盾构管片选型模型与系统实现[J].大地测量与地球动力学,2008,(6):112-116.(Liu Chun,et al.Rings prediction model in construction of long distance tunnel shield and its computing system[J].Journal of Geodesy and Geodynamics,2008,(6):112-116)

