蒙特卡罗法在海上某油田储量评价中的应用

罗文生，孙立春，郑洪印，蒋百召，武 静

（1.中海石油伊拉克有限公司，北京100010；2.中海油研究总院，北京100027）

蒙特卡罗法在海上某油田储量评价中的应用

罗文生1，孙立春2，郑洪印1，蒋百召2，武 静2

（1.中海石油伊拉克有限公司，北京100010；2.中海油研究总院，北京100027）

在油田开发前期的地质储量计算过程中，由于掌握的地质资料较少，采用确定法很难准确求取各储量计算参数，导致储量计算结果存在较大的不确定性。在介绍蒙特卡罗法原理、研究思路及研究方法，并对关键环节进行重点剖析的基础上，以海上某油田为例，通过卡方检验函数优选出各储量计算参数的概率分布数学模型，对整个地质储量进行随机模拟，确定储量的高、中、低方案值，并开展了储量敏感性研究；最后对该方法的适用性进行探讨。研究表明：在地质分析的基础上，且保证评价资料样本点充足的前提下，有效应用蒙特卡罗法，能够更客观地反映储量的评价结果，同时该方法可为开发前期或初期阶段国内外油气资源的同类评估提供指导。

蒙特卡罗法；地质储量；卡方检验；敏感性分析

0 引言

蒙特卡罗法是概率统计方法或随机模拟方法中最为常用的一种，该方法的发展始于20世纪40年代［1-2］，20世纪80年代左右被引入国内，并迅速在各领域广泛应用，同时也被应用于油田资源量、地质储量以及可采储量评估当中［3-8］。在油田开发前期或早期，尤其是海洋油气勘探开发具有三高（高风险、高投入、高科技）特点，在地质储量评价过程中经常面临钻井少、分析化验资料不足和动态测试结果有限等弊端，导致地质认识不清，储量计算参数存在多解性［9-13］，储量规模难以准确把握，最终影响油田经济性评价，因此有必要在该阶段开展蒙特卡罗法储量评价。笔者通过大量文献调研，发现前人仅对蒙特卡罗法原理及应用进行了大量研究和探讨［1-8，10-12，14］，而对储量计算参数样本预处理、概率分布模型的确定、结果输出及误差分析等储量不确定分析的关键环节阐述较少。因此，本文以开发初期阶段西非海上深水油田为例，重点阐述蒙特卡罗法的关键技术环节，剖析对比其与确定性方法之间的差异，并对该方法的可靠性和适用性进行深入探讨，对今后处于开发前期或初期阶段的海上油气田开发评价均具有借鉴作用。

1 原理及方法

蒙特卡罗法作为一种油气储量不确定性评估方法，它是以随机变量为对象，以概率统计为理论基础，通过对随机变量的概率模拟、统计实验来近似求解的一种方法［6］。该方法最大优点是只要提供储量参数的分布范围和分布函数，便可借助于数学方法，在计算机上通过随机数抽样模拟实验，进而对储量结果提出不同程度的可供应用的区间分布范围［15］。

1.1 蒙特卡罗法基本原理[14]

蒙特卡罗法的基本思想可概括为：欲求预测问题的数值解，则先构造一个表征预测问题的数学概率模型式，即

式中：X1，X2，…，Xi，…，Xn代表n个独立随机变量，其概率分布分别为Q1（X1），Q2（X2），…，Qi（Xi），…，Qn（Xn）。

使要求得的数值解恰好是概率模型式的某个数字特征（如数学期望等），而这个数字特征又可用统计方法求得其估计值，把这个估计值作为预测问题的近似值。对每个Xi依照概率Qi（Xi）进行随机抽样，组合变量后进行指标插值和计算，可得到一系列的目标值，当抽样次数足够多时即可得到系统值的概率分布，进而反映问题解的特征。

1.2 储量计算公式及流程

蒙特卡罗法和确定性法计算的储量公式均为容积法公式。

式中：OOIP为石油地质储量，万m3；GRV为岩石总体积，km3；NTG为净毛比，小数；POR为储层孔隙度，%；So为含油饱和度，%；Bo为原油体积系数，小数。

应用蒙特卡罗法计算储量时，储量计算参数可定义为具有一定取值范围的随机变量，而不是定值。计算储量的具体步骤可分为以下4步：①收集整理与储量计算相关的油田地质资料，在此基础上对各储量计算参数样本点分别进行数理统计分析；②建立符合这些参数统计规律的数学模型（概率密度函数），通过卡方检验函数优选出各储量计算参数样本点与各分布函数之间拟合误差最小的数学模型作为最优概率密度函数，同时输出各储量计算参数最优概率密度函数的P10（高方案）、P50（中方案）、P90（低方案）值；③通过计算机产生的伪随机数进行随机抽样模拟计算，随机模拟2 000次，依次得出单个储量计算单元的储量概率累积分布曲线，再对组合计算单元的储量进行概率叠加，最终得到油田总储量概率累积分布曲线，并输出总储量概率计算结果的P10，P50，P90值；④开展储量参数敏感性分析，以及尝试增加随机模拟次数来不断提高储量概率法的计算精度。

1.3 样本选取及预处理原则

选择影响储量变化的5个参数作为样本种类，即岩石总体积、净毛比、孔隙度、含油饱和度及原油体积系数。其中，岩石总体积（GRV）的大小主要受构造、油水界面和岩性边界等因素的影响。在选取样本点时，综合考虑每个储量计算单元相应顶底面构造幅度、岩性边界以及油水界面的变化范围，在构造模型中随机模拟计算200次得到样本。净毛比参数的样本应选取储量计算单元内所有钻遇井的井点值；储层孔隙度和含油饱和度分别选取储量计算单元内所有钻遇井的测井物性结果的数据作为样本；原油体积系数选取实验值，一般为确定值。

在统计好各参数样本点之后，以及进行概率密度函数选取之前，需针对样本点进行预处理，即当样本点个数足够多的情况下，可以直接进行概率密度函数拟合；当样本点个数较少情况下，可以采用对样本点进行复制重复翻倍的方法，以满足数理统计要求。

1.4 样本概率密度函数选取及结果输出原则

1.4.1 概率密度函数选取

为描述储量参数变量，在数学上通常使用概率密度函数f（x）和累积分布函数F（x）这2个概念，而在实际工作中通常用逆累积分布函数计算储量的期望曲线［6，16］。常用的概率密度函数具有以下几种类型：正态分布密度函数、三角分布密度函数、对数正态分布密度函数、均匀分布密度函数、指数分布密度函数及贝塔分布密度函数等，具体公式表达在此不再赘述［4，6-7］。

在选取各类样本点的概率密度函数时，利用卡方（Chi-square，简称χ2）、柯尔莫哥洛夫-斯米尔诺夫（Kolmogorof-Smirnov，简称K-S）、安德森-达林（Anderson-Darling，简称A-D）等检验函数进行拟合优度检验（goodness of tests），统计样本实际观测值与理论期望值之间的偏离程度，选取拟合误差最小的概率密度函数为该类样本点的数学模型［18］。其中最为常用的检验方式是卡方检验函数。

卡方检验统计量公式为

式中：χ2为卡方检验值；foi为第i组观测频数；fei为第i组期望频数；k为数据组数。

在拟合优度检验分析过程中，如果卡方检验值越小，代表拟合误差越小，拟合状态越好。以某储量计算单元46个孔隙度样本点为例，在建立概率分布数学模型过程中，通过卡方检验函数进行拟合优度检验，发现正态分布密度函数卡方值最小，为2.6957，表明该数学函数模型拟合优良（图1和表1）。

图1 卡方检验孔隙度概率密度函数图Fig.1 Theporosity probability density function histogram by Chi-square test

表1 各概率密度函数的卡方检验数据表Table 1 TheChi-square test resultsof different probability density functions

1.4.2 样本结果输出原则

（1）截断处理原则

拟合后概率密度函数范围往往会超出合理值范围，如孔隙度和含油饱和度分布范围超出有效厚度下限标准范围，NTG＜0或＞1等。因此，需要对概率密度函数进行截断处理，以保证参数变量分布区间的合理性。

（2）相关性原则

一般而言，储量计算中各参数是相互独立分布的随机变量，而孔隙度和含油饱和度的分布则具有一定的相关性。因此，对孔隙度和含油饱和度这2类样本首先要进行相关性分析，拟合出两者之间的相关系数，从而对含油饱和度概率密度分布进行条件性约束。

1.5 储量计算结果敏感性分析原则

对储量计算结果进行敏感性分析时，采用单因素分析原则，即分析各因素对整个结果的影响程度。敏感性分析是假设每次仅有其中一个因素作为变量，其他因素保持P50值不变，以分析此可变因素对结果的影响权重。最终各因素对储量计算结果的相对敏感程度，可以通过旋风图或蜘蛛图来反映。

2 实例剖析

A油田位于西非海上深水区，油田水深1 300～1 450m。目的层自上而下细分为Ⅰ，Ⅱ和Ⅲ共3个油组。构造为一受断层切割，向四周倾伏的断裂背斜。储层为深水浊积水道沉积，岩性主要为细—粗粒砂岩，储层孔隙度为18%～30%，平均为22.6%，渗透率为200～4 000mD，平均为1 100mD，储层具有中孔、中高渗特征。储量评价阶段采用确定性容积法计算的石油地质储量为2 497.65万m3。目前该油田处于开发初期。

2.1 概率密度函数确定

在收集3个储量计算单元（Ⅰ，Ⅱ和Ⅲ油组）各储量参数GRV，NTG，POR，So和Bo样本点并进行预处理的基础上，通过卡方拟合优度检验，优选出卡方值最小的密度分布函数作为其概率分布数学模型，并输出各油组及各储量参数的P10，P50和P90值，分别作为储量不确定分析的高、中、低方案值（表2）。其中，GRV，NTG，POR和So均利用样本点进行了概率密度函数选取，其结果表现为贝塔分布和正态分布共2种类型，Bo则利用实验室测量定值。

表2 A油田蒙特卡罗法计算石油地质储量表Table 2 TheOOIP calculation resultsof A oilfield by M onte-Carlomethod

2.2 储量计算结果及对比

利用蒙特卡罗法对参数数学模型进行随机抽样模拟计算，并通过专业软件随机运算20 000次，分别计算了3个储量计算单元以及组合计算单元共4个模型的石油地质储量期望曲线，其中期望曲线概率为10%～90%时可作为其储量置信区间（图2、参见表2）。计算结果表明：①组合单元计算模型P90概率储量比各单元P90概率储量简单算术求和值要大，组合单元计算模型P10概率储量比各单元P10概率储量简单算术求和值要小（参见表2），这恰恰反应了概率法储量计算的特点；②将其中方案P50（最可能值）与确定法计算值进行对比（表3），认为Ⅰ，Ⅲ油组以及组合计算单元储量，采用2类方法计算的储量变化率绝对值都≤10%，Ⅱ油组计算单元储量利用蒙特卡罗法比确定法减少226.62万m3，减少率为15%。综上所述，除Ⅱ油组以外的其他储量计算单元，利用蒙特卡罗法可以为储量的不确定性计算降低风险。

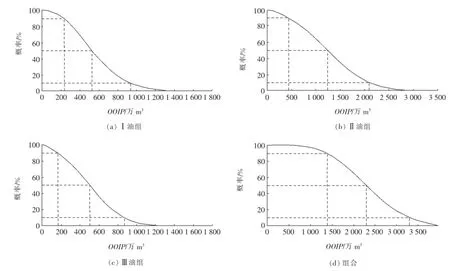
图2 蒙特卡罗法计算各单元以及组合单元石油地质储量累积概率分布图Fig.2 The OOIP cumulative probability distribution chart of each group and association by M onte-Carlom ethod

表3 不同方法计算石油地质储量对比表Table 3 TheOOIP calculation resu ltsby differentmethods

2.3 储量误差及敏感性分析

根据蒙特卡罗法计算储量与确定法对比，发现Ⅱ油组计算误差相对较大。通过储量计算结果敏感性分析（图3），影响储量大小的主要参数为NTG值，其对储量计算结果的贡献率为81.7%。因此，NTG值概率法在取值上的误差应该是导致该单元储量计算误差较大的原因。

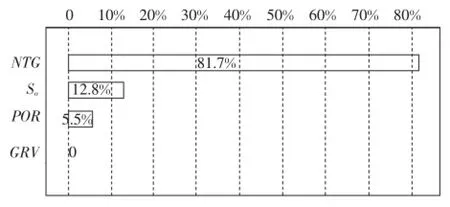
图3 Ⅱ油组储量敏感性分析旋风图Fig.3 The sensitivity analysis tornado chartofOOIPofoilgroupⅡ

2.3.1 取值方法差异

通常，确定性法是综合考虑地质储量的落实程度以及开发井对地质储量的动用程度，平面上分井区、分断块，最终采用等值线面积权衡法来计算NTG（或有效厚度）值。而本次蒙特卡罗法并没有考虑平面上分井区、分断块，而是由该油组内所有砂体钻遇井的NTG值直接参与样本统计。

对Ⅱ油组而言，通过反算得出确定性法NTG的平均值为0.54，而采用蒙特卡罗法计算P50概率的NTG值为0.44，可以发现后者计算NTG值偏小。

2.3.2 相带分布差异

该油田储层为深水浊积水道沉积（图4），在不同的沉积微相位置，分别钻遇水道和水道天然堤的井具有不同砂、泥岩分布特征，即不同NTG值，再加上不同相带控制的含油面积不同，则该相带由钻井得到的NTG值所占的权重也应该不同。

图4 深水浊积水道沉积剖面示意图Fig.4 The profile for deepwater turbidite channel

另外，Ⅱ油组砂体并不是由单个水道砂体构成，而是多期水道侧向迁移、纵向叠置的结果。当前钻井所揭示的水道砂体的中心位置不一定是砂体发育最好以及NTG高值的位置［19］。由于水道沉积的多期迁移叠置及样本点较少，造成井点NTG值在平面分布上不均匀，这也是造成NTG值的样本点直接参与统计分析不合理的原因之一。

2.3.3 实钻井数限制

通常来说，当原始样本点较多时（一般＞30个），称作大样本容量。针对大样本容量，利用频率统计法拟合求得的概率密度函数可靠性较高，因为其原始数据均来自于实际资料［18，20］。

对Ⅱ油组而言，由于开发早期，实钻井数少（11口）且分布不均匀，NTG低值样本点比例又相对较高，即落入NTG值较小区间的频率统计值较大，最终导致定义的概率密度函数不合理，则蒙特卡罗法计算的P50概率值偏小（表4）。

表4 Ⅱ油组井点NTG值分布频率表Table 4 The NTG distribution frequency of oilgroupⅡ

综上所述，在蒙特卡罗法随机模拟储量结果的过程中，取值方法差异、相带分布差异及钻井井数限制，共同造成Ⅱ油组NTG取值区间跨度大、分布不均，给模拟结果的可靠性带来较大误差。如果将其归结为数学问题的话，其根本原因就是由于Ⅱ油组NTG值的样本容量不足导致样本点分布不均。

3 结论及建议

（1）蒙特卡罗法相比于确定性法，实现了由地质参数的不确定性而给出可能的储量结果变化范围，使得储量评价结果更客观、更具决策性，尤其对开发前期或初期海上投资风险较大的油气资源更是如此。

（2）用蒙特卡罗法计算的储量能大大降低各储量计算单元直接求和产生的误差。储量敏感性分析为蒙特卡罗法计算储量误差分析提供了有利手段。

（3）蒙特卡罗法计算的精度首先是通过大样本容量来作保证的，其次是通过卡方检验函数优选出准确的概率分布模型。而对于小样本容量参数，无法利用经验函数拟合出准确的分布模型，建议尝试运用判断建模法，将样本参数作三角分布函数处理，求取其极大、极小值，估计其最可能值，实现储量的实验性概率计算及拟合。

［1］徐钟济.蒙特卡罗法［M］.上海：上海科学技术出版社，1985：1-4.

［2］方再根.计算机模拟和蒙特卡洛方法［M］.北京：北京工业学院出版社，1988：1-4.

［3］裴鹿成，王仲奇.蒙特卡罗法及应用［M］.北京：海洋出版社，1988：2-9.

［4］徐耀宗.蒙特卡洛法在石油资源量估算中的应用［J］.石油勘探与开发，1987，10（2）：34-36.

［5］王才经，乐友喜.Monte Carlo方法预测区带资源量［J］.石油大学学报：自然科学版，2000，24（1）：104-105.

［6］文环明，肖慈珣，李薇，等.蒙特卡洛法在油气储量估算中的应用［J］.成都理工学院学报，2002，29（5）：487-489.

［7］张明，张建云，金菊良，等.蒙特卡罗法求解湖库未确知水环境容量［J］.水电能源科学，2008，26（6）：33-34.

［8］高济稷，白国平，秦养珍，等.蒙特卡洛模拟法在也门马里卜—夏布瓦盆地中的应用［J］.石油实验地质，2010，32（3）：305-306.

［9］毕海滨，查全衡，王永卓.提高储量评估水平的三大地质要素［J］.石油学报，2004，25（1）：26-27.

［10］孙立春，高博禹，李敬功.储层地质建模参数不确定性研究方法探讨［J］.中国海上油气，2009，21（1）：35-36.

［11］高博禹，孙立春，胡光义，等.基于砂控地质建模和Monte Carlo模拟的储量评价方法［J］.中国海上油气，2009，21（2）：109-110.

［12］薛艳霞，廖新武，赵春明，等.基于随机建模技术的油田开发初期河流相储层不确定性分析方法——以渤海A油田为例［J］.岩性油气藏，2012，24（1）：80-81.

［13］苏进昌，张岚，马新福.河流相储层开发初期地质建模［J］.岩性油气藏，2008，20（3）：114-115.

［14］郑家朋.基于蒙特卡洛方法的提高原油采收率潜力风险性评价［J］.石油天然气学报，2010，32（1）：343-344.

［15］谭向农，董广华.蒙特卡洛模拟在准噶尔盆地资源评价应用中的有关问题研究[J].新疆石油地质，1986，7（1）：94-95.

［16］吕晓光，张永庆，陈兵，等.深度开发油田确定性与随机建模结合的相控建模［J］.石油学报，2004，25（5）：61-62.

［17］Charnes JM.FinancialModelingwith Crystal Balland Excel［M］. USA：JohnWiley&Sons，Inc.，2007：202-234.

［18］埃文斯，奥尔森.模拟与风险分析［M］.洪锡熙，译.上海：上海人民出版社，2001：60-81.

［19］赵晓明，吴胜和，刘丽.尼日尔三角洲盆地Akpo油田新近系深水浊积水道储层构型表征［J］.石油学报，2012，33（6）：1051-1055.

［20］李从玲.对蒙特卡洛模拟中三角分布法的改进和应用［J］.海洋地质与第四纪地质，1989，9（4）：98-99.

（本文编辑：杨琦）

App lication ofM onte-Carlomethod to OOIP estimation of an offshoreoilfield

LUOWensheng1，SUN Lichun2，ZHENGHongyin1，JIANG Baizhao2，WU Jing2
（1.CNOOC Iraq Limited，Beijing100010，China；2.CNOOCResearch Institute，Beijing100027，China）

Itisdifficult toascertain everyparametersoftheOOIPcalculation bydeterminationmethod especially in the initial oilfield development stage because of the limitation of geological data.This paper presented the principle, workflow,and researchmethod ofMonte-Carlomethod,and analyzed the key points.Taking an offshore oilfield as an example,this paper optimized the best probability distribution model of OOIP calculation parameters through Chisquare test function,determined the high,middle and low values of OOIP parameters by random simulation,and estimated thesensitivity.Theapplicability of theMonte-Carlomethodwasdiscussed finally.Thestudy resultsshow that theMonte-Carlomethod isaveryeffectivemethod toestimate theuncertainty ofOOIPbased on geologicalanalysisand abundant data sample number,and the method is helpful for estimation of similar oil and gas field in the initial developmentstage.

Monte-Carlomethod；OOIP；Chi-square test；sensitivityanalysis

TE155 < class="emphasis_bold">文献标志码：A

A

1673-8926（2014）01-0105-05

2013-11-04；

2013-12-13

国家重大科技专项“西非、亚太及南美典型油气田开发关键技术研究”（编号：2011ZX05030-005）资助

罗文生（1981-），男，硕士，工程师，主要从事油气田开发综合地质、油藏描述研究工作。地址：（100010）北京市东城区朝阳门内大街2号凯恒中心B座19层。E-mail：luowsh2@cnooc.com.cn。