一种基于二次型约束的最优对角加载量的计算方法*

郑玉伟，张春良，岳 夏，刘 凯，朱厚耀

（1.南华大学机械工程学院，湖南衡阳 421000；2.广州大学机械与电气工程学院，广东广州 510006）

一种基于二次型约束的最优对角加载量的计算方法*

郑玉伟1，张春良2，岳 夏2，刘 凯1，朱厚耀2

（1.南华大学机械工程学院，湖南衡阳 421000；2.广州大学机械与电气工程学院，广东广州 510006）

对角线加载技术可以使自适应波束形成器在失配情况下仍然能保持良好的性能，但是加载量的确定却没有一个严格的标准。采用一个二次型约束来讨论对角加载问题。将加载水平同权值模的约束条件联系起来，通过迭代的方法求出最优加载水平。该方法不需要知晓信号的先验信息，其具有更好的灵活性与适用性。仿真结果表明：最优加载在不同信噪比，较少快拍情况下均具有较好的稳健性，且在模糊环境下更容易实现。

阵列信号处理；波束形成；DOA失配；对角加载；鲁棒性

0 引言

波束形成技术广泛应用于声纳、雷达和通讯系统中，长久以来研究者们致力于优秀算法的研究，其中MVDR、MUSIC和ESPRIT的方法不断将波束形成技术推向更高的高度。在波束形成器的设计过程中，信号的向导矢量以及空域谱矩阵均采用理想的模型，但是在现实使用中波束形成器是按照离散的步进方式改变向导矢量进行空域扫描，并且采用快拍采样协方差的方法估计空域谱矩阵。这将会造成波束形成器的失配，除此之外还有阵列扰动，波达方向失配等失配方式，都将造成波束形成的性能损失。

众多学者在增强波束形成器的鲁棒性方面也做出了许多卓越的成就。COX等人提出了一种对角加载的方法[1]，使得波束形成器在失配时更加稳健。Feldman等人提出了基于特征空间方法[2]，但是当子空间维数不确定或者SNR较低时，该方法有较为严重的性能衰落。Gershman等人基于加宽波束零陷带的思想，提出了独立数据微分约束法[3]。Bell等人提出基于贝叶斯方法的自适应算法，能在阵列接收信号与期望信号DOA的先验信息之间取得一种平衡。其中，对角加载方法是最为常见一种，但是加载量的确定一直是一个比较困难的问题。文献[4]分析了对角加载对自适应阵列SINR和INR性能的影响，研究加载量的门限选取问题，该方法是对预计的SINR和INR的水平有有足够的信息，而选择一个固定的适合的对角加载量。但是在现实中没有足够的先验信息来确定固定的加载量。文献[5]研究波束畸变的根本原因，根据接收信号协方差矩阵的结构特点，讨论了小特征值λ与加载量的关系。但是在门限的选取和加载量的确定仍然没有明确的说明。

1 基于二次型约束的对角加载

假设线性均匀阵列，阵元数为M，有K个不相干的信号源。

信号模型：

其 中 ， X(t)=[x0(t)，x1(t)，···，xM-1(t)]T，A=[a(θ1),a(θ2)，···,a(θk)]，a(θ)为阵列流矢量，N为背景噪声。

阵列输出：

其中，w=[w1,w2,···,wM]T，为阵列信号的加权矢量。

输出功率谱：

其中R为接收信号的协方差矩阵R=E[x(t)xH(t)]，在现实实现中，通常采用快拍采样估计其协方差矩阵

最小方差无畸变响应（Mvdr）的最优权矢量

所以针对失配问题，在阵列设计时，增加一个敏感度约束，即T≤T0。

则，二次型约束优化问题可以表示为，

根据拉格朗日乘子算法解得

上式与参考文献[7]中加载模型一致。同时可以看出，加载水平λ与T的选择有关。在前面提到的文献中，加权水平都是根据信号先验信息直接给出的，并没有将其与加权的模的原约束值以及敏感度T联系起来。

下面将通过二次型约束问题，求出最优加载值与敏感度以及加权模值得关系。

在上式中，施加的一次约束条件，是约束期望信号无畸变的通过波束形成器，但是在现实实现中，接收信号是由可能的多个期望信号、干扰信号以及噪声复合的信息，为了使全部的期望信号按照一定的准则通过波束形成器，获得最佳的波束形成，需要施加更多的约束条件。那么该问题的一次约束就转化为了灵活度更大、适用性更广的线性约束问题。下面将通过研究二次型线性约束问题，确定最佳的加载水平。

LCMV优化问题：

一次约束条件问线性约束：

二次约束条件：

其中，C是一个N×M维的约束矩，g为约束值。例如，如果希望感兴趣的K个信号无畸变地通过波束形成器，则此时的约束矩阵C=[a(θ1),a(θ2),···,a(θK)]，约束值g=[1,1,···,1]Tk×1。

首先研究T0所允许的取值范围。

先解出等式约束问题，即wHw=T0。

线性约束的一个等效的实现结构为广义旁瓣对消器[7]。则把最优解wopt表示为广义旁瓣对消器的形式，

其中PC是wopt向约束子空间的投影PC=C[CTC]-1CH，P⊥C是wopt向约束空间的正交空间投影。

所以

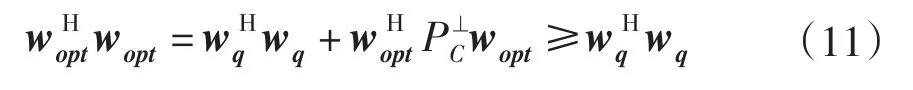
故，有

因此，

即

所以设置的约束值不能小于gH(CHC)-1g。现在解优化问题，

由Lagrange乘子算法解出，

定义

并为了强调不等式约束关系，定义

有广义旁瓣对消结构，最优权矢量可以表示如下：

其中，阻塞矩阵B满足BHC=0。注意B并不是唯一的，构造B的一个方法是P⊥C来确定，并且结果满足BHB=I，

则

首先把式（22）写为

其中，Rz=BHRB，是z的谱矩阵，z是阻塞矩阵的输出，且pz=BHRwq，

当λ≥0时，对角加载数据矩阵(R+λI)是正定的，在上式的中的导数值是负值。即λ＞0时，权矢量的模随着λ增大而减小。

现在求满足不等式的约束情况的λ：

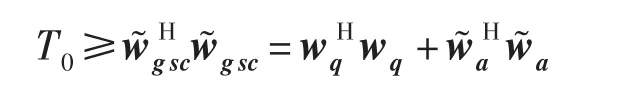
或

接下来将使用数值方法求解对角加载量的与二次型约束之间的关系。

开始有λ0=0；令λ1=λ0+Δλ且有

算法总结：

（1）由二次型约束构建线性约束问题；

（2）由约束条件确定二次约束的门限值T0；

（3）构造阻塞矩阵B，使其满足BHC=0, BHB=I，并且求出wq与a表达式；

（4）根据求得的公式和条件，使用迭代法求出最优加载量λopt。

2 仿真分析

仿真1，采用16阵元均匀线阵，阵列间距为半波长，，背景噪声为高斯白噪声。DOA（波达方向）分别取-20，-10，0，20，30，60。期望的DOA为0，快拍次数为1 000。比较在T0条件下对角加载前后的无畸变约束下波束形成方向图。这里取T0=0.15，因为无畸变约束下的白噪声最大增益为均匀加权时的增益N，对于任意非均匀加权，都有

由图1～4可以看出，在较低信噪比的情况下，阵列信号的扰动不是很明显，加载前后的波束方向如没有明显变化，但是，随着信噪比的提高，阵列信号失配逐渐增大，波束方向图失真也更加严重，由图4可以清楚的看到，加载前方向图严重失真，几乎无法获得期望的DOA，而加载后的波束方向图仍然具有良好的保形性。对失配环境具有较好的稳健性。再者，比较不同信噪比条件下，加载后的波束方向图，不管信噪比如何变化，加载后的波束方向图都没有太大的变化，所以在不知道信号先验信息的情况下，二次型约束最优加载具有更好的适用性。

图1 SNR=-10的波束方向图

图2 SNR=0的波束方向图

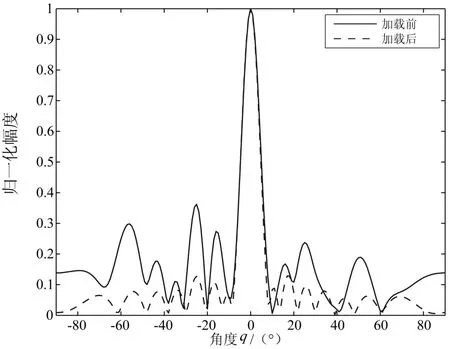
图3 SNR=10的波束方向图

图4 SNR=20的波束方向图

图5 SNR=-10情况下的波束方向图

图6 SNR=10情况下的波束方向图

仿真2，取快拍次数N=40，其他仿真条件与仿真以相同，比较SNR=-10，10情况下，加载前后的波束方向图。

如图5所示，在快拍次数较少时，即使在较低的信噪比的情况下，加载前已不能较好的实现波束形成，而加载后的情况有明显改善；如图六示，并与图3比较，在快拍次数较多的情况下，加载前后的波束方向图相近，只是加载后的保形性更好，但是，在快拍较少的情况下，加载前的波束形成已经失效，而加载后的波束方向图依然保持较好的性能。

3 结论

通过以上的仿真分析可知，在估计协方差矩阵的采样快拍次数有限，且信号的先验信息未知的情况下，通过二次型约束确定的最优加载量，能够有效的提高波束形成的稳健性，并且由于其不需要知晓信号先验信息，所以该方法具有更广泛的适用性和灵活性。

［1］H.COX Resolving power and sensitivity to mismatch of optimum array processors［J］.J.Acoust.Soc.Am.，vol.ASSP-54，pp.771-785，September 1973.

［2］Feldman D D，Griffith L J.A project approach for robust adaptive beam-forming［J］.IEEE Trans Signal Process⁃ ing，1994（42）：867-876.

［3］ Gershman A B， Nickel U，Bohme J F.A adaptive beam-forming algorithms with robustness against jammer motion［J］.IEEE Trans Signal Processing， 1997（45）：1878-1885.

［4］陈晓初.自适应阵对角加载研究［J］.电子学报，1998，26（4）：29-35.

［5］张小飞，徐大专.自适应对角线加载波束形成算法［J］.中国空间科学技术，2007，4（2）：66-71.

［6］Harry L.Van Trees.Optimum Array Processing Part IV of Detection， Estimation，and Modulation Theory［M］. ISBN 978-7-302-14760-2.

［7］张小飞，汪飞，徐大专.阵列信号处理的理论与应用［M］.北京：国防工业出版社，2010.

［8］谢斌斌.稳健波束形成算法研究［D］.成都：电子科技大学，2012.

［9］蒋留兵，罗良桂，车俐.频率不变约束的对角加载稳健宽带波束形成算法［J］.现代雷达，2012，12（34）：41-45.

［10］史英春，钟子发，邹翔，等.基于范数优化的对角加载稳健自适应波束形成［J］.电路与系统学报，2013，18（1）：218-224.

A Method of Calculating the Optimal Diagonal Loading Based on a Quadratic Constraint

ZHENG Yu-wei1，ZHANG Chun-liang2，YUE Xia2，LIU Kai1，ZHU Hou-yao2
（1.School of Mechanical Engineering，University of South China，Hengyang421000，China；2.School of Mechanical and Electrical Engineering，Guangzhou University，Guangzhou510006，China）

Diagonal loading technique can make the adaptive beam-forming keep good performance in the case of mismatch，but there is not a strict standard in the determination of the loading quantity.This paper uses a quadratic constraint to discuss diagonal loading problems.The loading level will associate with the constraint conditions of weight module，and then calculate the optimal loading quantity by iteration.This method does not need to know the specific priori information of signal，so it is more flexible and applicative.Simulation results show that optimal load has better robustness in the case of both different SNR and less snap，and it is easier to implement in a fuzzy environment.

array signal processing；beam-forming；DOA mismatch；diagonal loading；robustness

TN957.51

A

1009－9492(2014)01－0021－05

10.3969/j.issn.1009-9492.2014.01.006

郑玉伟，男，1989年生，安徽六安人，硕士研究生。研究领域：故障诊断。

(编辑：向 飞)

张春良，男，1964年生，教授，博士生导师。研究领域：设备状态监测与故障诊断，制造过程自动化，微制造技术，激光加工技术，数控技术等。

*国家自然科学基金（编号：51275099/E050302）；广东省自然科学基金项目（编号：S2012010009505）

2013－07－12