基于传递矩阵法的磁悬浮轴承转子的动力学分析*

宋骏琛，欧阳慧珉，张广明

（南京工业大学，江苏南京 211816）

基于传递矩阵法的磁悬浮轴承转子的动力学分析*

宋骏琛，欧阳慧珉，张广明

（南京工业大学，江苏南京 211816）

转子是磁悬浮轴承系统旋转机械的核心部件，其性能与系统稳定性及各项技术指标紧密相连。提升转子动态性能已成为当务之急。以磁悬浮开关磁阻电机的磁轴承转子为例，通过普劳尔传递矩阵法和MATLAB强大的绘图功能分别就柔性、刚性两种不同状态下的支承，计算出了该轴系的固有频率及临界转速，并得到了相应的主振型图。

磁悬浮轴承；传递矩阵；动态性能；固有频率；临界转速

0 引言

随着工业技术的不断飞跃，磁悬浮轴承转子技术以其无磨损、无接触、转速高等特点，已广泛应用于能源、航空等领域。转子动力学性能的分析与设计是直接决定整个系统性能的重要内容之一，而磁悬浮轴承转子动态性能的好坏更直接关系到系统运作的安全性能与工作效率。在磁轴承转子运转的过程中，转子的转速甚至超过了本身的临界转速而发生了共振的危险，因此有效抑制其工作转速超过临界转速的动力学分析研究刻不容缓。

磁悬浮轴承转子的动态特性通常包括临界转速的计算，振型图的分析及如何动平衡。传递矩阵法占据内存少，编程通俗易懂，矩阵的阶数不随系统自由度的增大而增大，特别适用于转子系列的链式系统。本文使用普劳尔传递矩阵法对磁悬浮轴承开关磁阻电机的转子系统进行动力学分析，利用磁悬浮轴承刚度可调节的特点分别针对柔性支承，刚性支承的临界转速做出了分析，以达到最优动态特性的稳定悬浮。

1 动力学分析

1.1 模型的建立

磁悬浮轴承转子系统因其工作状态下的高速运转而被视为质量连续分布的弹性系统，具有无穷多个自由度，其支撑方式也视为弹性支撑。传递矩阵法通常将磁轴承转子系统离散为N个轴段，简化为具有若干集中质量的多自由度系统[1]。该系统由带弹性支承的多刚性薄圆盘和无质量等截面的弹性轴段组成。以该磁悬浮轴承系统为例，转子系统主要包括飞轮、两径向磁悬浮轴承、主轴变频电机及主轴本体。磁悬浮转轴转速通常状态比一般转轴快很多，应对固有频率进行精细的计算，考虑到简化模型质量块越多结果越精细，故不妨简化为图1所示多圆盘等截面轴段结构示意图。

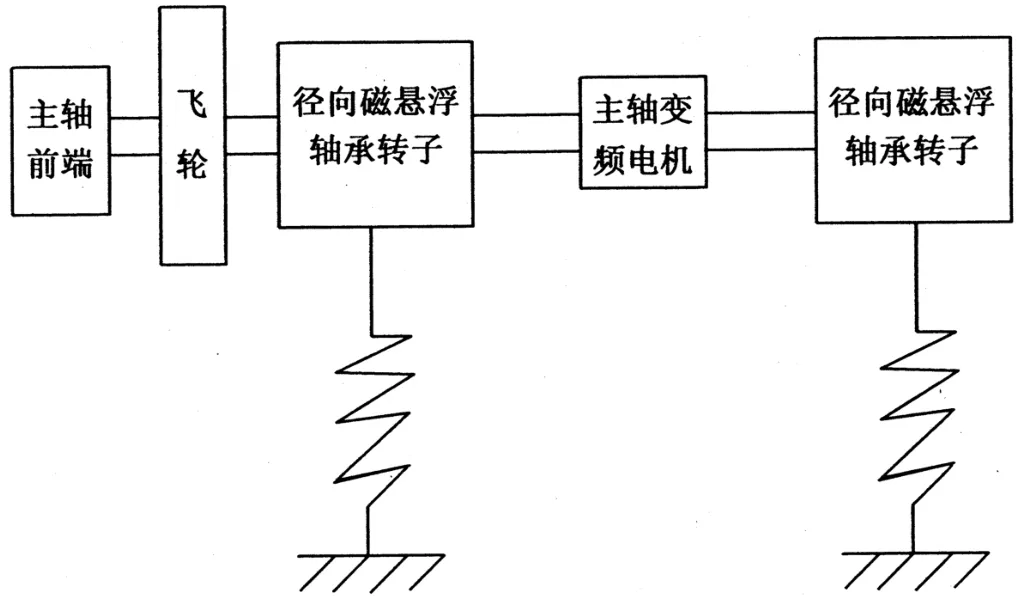
图1 多圆盘等截面轴段结构示意图

根据图1所示结构示意图，再考虑到由于轴系的固有频率（临界转速）和振型与磁轴承系统质量分布有关，所以简化后的模型质量，也就是圆盘的集质量应尽量与磁轴承转子系统质量接近。图2为磁悬浮转子系统简化离散模型。本方法为沿着轴线将转子离散为27个轴段，即有28个质量单元。按质心不变原则分配到轴段两端截面上。

图2 磁悬浮转子简化模型

1.2 单元传递矩阵的建立

建立单元矩阵之前，需先对圆盘与轴段分别作受力分析，最后再通过两者结合的组合构件做出分析。

对于磁轴承转子的第i个截面，设状态向量为Zi，由径向位移Yi，挠角αi，弯矩Mi及剪力Qi所组成[2]，满足关系式Z=[Y,α,M,Q]T。任一轴段左右节点之间的状态向量都存在一定的关系，即Zi+1=TiZi。为了便于分析计算，圆盘与轴段通常组合成一个统一构件。由达朗贝尔原理可分别得出圆盘与轴段的传递矩阵。

图3 圆盘轴段的组合件分析

带弹性支撑有质量的圆盘单元传递矩阵为：

无质量等截面的弹性轴段传递矩阵为：

上两者组合公式为Ti=BiDi即为：

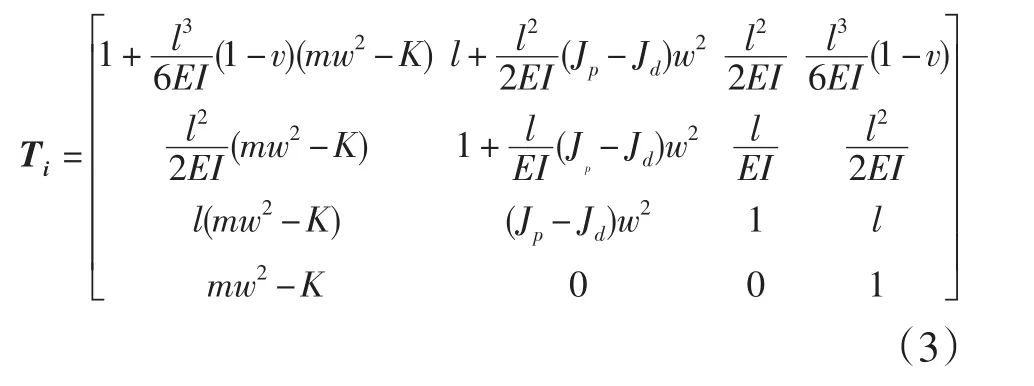
m为单元薄圆盘的集质量，l为单元轴段的长度，Jp、Jd分别为单元直径转动惯量，单元极转动惯量，w为转子角速度，K为支撑处刚度，这里v为考虑剪切影响的系数，a为截面系数，考虑到该磁轴承转子系统为实心圆轴，故取a=0.886；A为截面积，EI为材料弹性模量与轴段截面矩之积。

1.3 固有频率的计算

基于本文所建立的模型，加上磁悬浮转子系统转轴两端均为自由端，可知状态向量符合边界条件：由轴段与圆盘组合建立的矩阵可知任一截面有Zn=Tn-1Tn-2...Z1，将Z1、Zn带入上表达式可得出：

综合（4）（5）可知任一截面均需要满足边界条件Mn=0，Qn=0，那么磁悬浮轴承转子系统同步正进动时的频率方程式即为

此频率方程式通常使用频率扫描法来分析求解[3]，即按一定步长选定试探频率。通过矩阵连乘及剩余量的计算公式（6），便可求得对应于上述各试算频率的剩余量Δ(w2)。

如果相邻两试探频率的剩余量异号，则说明Δ(w2)和试探频率的关系曲线和试探频率为横坐标的w轴相交，那么必有一个频率方程式的根，为转子的各阶临界转速。即为一个满足边界条件的ω值。用二分法仔细搜索就可以逐步逼近求出临界转速。采用上述方法计算临界转速可通过观察Δ(w2)-w曲线来证明曲线的连续性，故只要选取合适的步长，便可用频率扫描法算出在指定频率范围内的所以临界转速。

1.4 支撑刚度对磁悬浮轴承转子系统的临界转速分析

径向磁悬浮轴承的支承刚度对磁悬浮轴承转子系统的固有频率的变化具有一定的影响，而磁悬浮轴承较普通轴承具有支承刚度可变的优势[4]。不同的径向刚度的数值对转子系统的各阶临界转速也有不同的影响。这里分别对所设计的磁轴承系统柔性、刚性支承做出考虑。

1.4.1 柔性支承状态下的固有频率分析

使用MATLAB编程计算临界转速和振型图，考虑到磁悬浮轴承转子工作状态下的高速运转，飞轮直径150 mm，轴长为440 mm。使用本文开头所示离散方法划分节点。取前后支承刚度为40 000 N/m，计算结果与振型如图4所示。

图4 基于柔性的磁悬浮轴承系统振型弯矩图

表1 基于柔性支撑的前几阶固有频率

如表1和图4可知前两阶模态表现为刚性，2阶弯曲发生微变，3阶呈现弯曲模态振型，而磁轴承转子系统最高转速已高于前两阶临界转速，故发生共振的几率大。

1.4.2 刚性支承状态下的固有频率分析

采用与上述同样的MATLAB编程，使用传递矩阵法，改变参数支撑刚度K的大小，设前后支承的径向位移为0，前后刚度都为10e6 N/m，弯矩图及表格见图5和表2。

Analyzing Dynamic Characteristic of High Speed Motorized Spindle on Magnetic Bearing Rotor

SONG Jun-chen，OUYang Hui-min，ZHANG Guang-ming
（Nanjing Tech University，Nanjing211816，China）

With its high speed，high effiency，the magnetic bearings-rotor system has become the core of modern rotating machinery system，Taking the magnetic bearing rotor of the bearingless switched reluctance motor as an example，by using Prohl transfer matrix method and the drawing function of MATLAB，according to the rigid support and flexible support respectively,the free frequency and critical speed of the spindle system was got,and the relative main vibration model was found.

magnetic bearings-rotor；transfer matrix；dynamic characteristics；free frequency；critical speed

图5 基于刚性的磁悬浮轴承系统振型弯矩图

TH133.3

：A

：1009－9492(2014)11－0011－03

10.3969/j.issn.1009-9492.2014.11.003

*国家自然科学基金项目（编号：51277092）江苏省基础研究计划（自然科学基金）资助项目(编号：BK20130938)

2014－05－09