基于HMM算法体系的逆维特比算法理论研究*

刘功生，张春良，岳 夏，朱厚耀

（1.南华大学机械工程学院，湖南衡阳 421001；2.广州大学机械与电气工程学院，广东广州 510006）

基于HMM算法体系的逆维特比算法理论研究*

刘功生1，张春良2，岳 夏2，朱厚耀2

（1.南华大学机械工程学院，湖南衡阳 421001；2.广州大学机械与电气工程学院，广东广州 510006）

隐马尔可夫模型（Hidden Markov Model，HMM）的基本算法体系主要包括Baum-Welch算法、前向-后向算法与Viterbi算法三大经典算法，通过展开对HMM新问题及新算法的理论研究，引出逆维特比问题及逆维特比算法的理论体系，并提出将逆维特比算法引入HMM基本算法体系中构建一种新的算法体系及一种新评估体系的构想，最后对新算法体系的应用进行了展望。

隐马尔科夫模型；逆维特比问题；逆维特比算法；评估体系

HMM本身是一个双随机过程，同时具有出色的动态过程建模能力[1]，因此HMM在语音识别、故障诊断及生物医学等领域获得了广泛的应用[2-4]。

在HMM经典算法体系中，Baum-Welch算法虽然已发展得相当成熟，但在实际应用中仍存在训练过程局部收敛及训练结果鲁棒性不足等缺点[5]。因此，寻求一种能对训练结果进行有效评价的方法将越显重要。在故障诊断领域中，HMM提供了一种以似然率大小作为训练模型性能好坏的评价标准的评估算法，但该评估方法存在似然率高时识别率不一定高的不足，即用似然率的高低来评价训练模型的性能好坏将会导致故障诊断结果存在一定的误判风险。因此进行HMM新算法的研究并建立新的评估算法将具有很高的研究价值。本文中将以故障诊断作为HMM的应用背景来展开对HMM新算法理论及新评估体系的研究。

1 HMM三大基本算法体系

1.1 HMM三大基本问题及算法

在HMM的基本理论框架中，HMM能用来求解的三大基本问题[6]为：学习问题、评估问题及解码问题。该三大基本问题可简单描述为：学习问题主要是获取给定观测值序列的HMM模型；评估问题主要是计算所获得的HMM模型与输入观测值序列的似然率；解码问题主要是在给定HMM模型情况下寻找对应观测值序列的最优状态序列。

在HMM的理论框架中同时也给出了求解以上三大基本问题的三大经典算法[6]：训练问题的Baum-Welch算法、评估问题的前向或后向算法、解码问题的Viterbi算法。此三大基本算法之间通过内在的联系构成了经典的HMM算法体系，如图1所示。

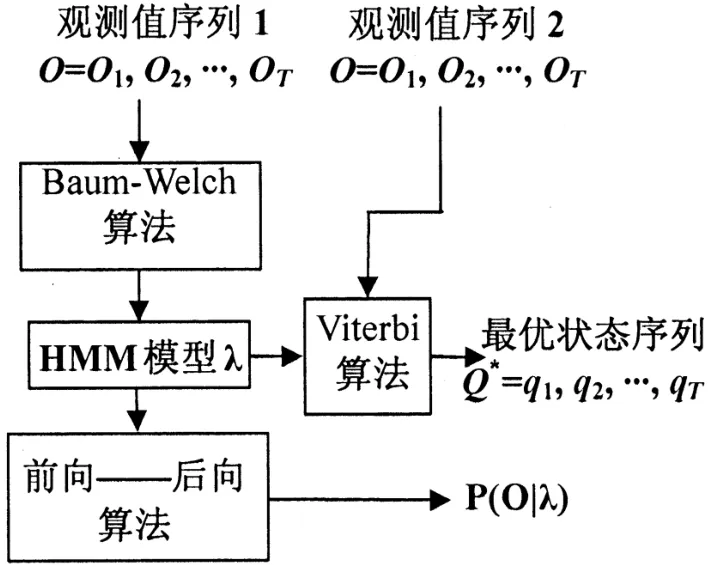
图1 HMM基本算法体系

图1中，对于机械故障诊断过程，观测序列1和观测序列2均是由采集到的故障样本通过特征提取获得，其中，观测序列1由用于训练的样本获得，观测序列2由用于测试的样本获得。观测序列1通过Baum-Welch训练算法可以获得相应状态的HMM模型λ，但由于该训练算法在迭代过程中存在易陷入局部收敛的不足，难以保证训练结果为最优。在设备状态识别过程中，不良的训练结果将会导致识别率下降，因此训练的结果需要预先进行模型性能的评估，性能较低的训练结果不能加入HMM模型库。HMM算法体系中提供了前向——后向算法作为训练结果的评估算法，对于性能评估良好的模型才能作为Viterbi算法的输入，用于进行设备运行状态的识别。

因此，三大经典算法通过其内在的联系联结在一起，构成了HMM的基本算法体系，并为故障诊断提供一种有效的算法模型。

1.2 维特比算法的实现过程

由于维特比问题的目的是要寻找给定模型λ和观测序列O的最优状态序列Q*，对应的viterbi算法[7-8]实现过程如下：

（1）首先定义两个变量：

（2）初始化定义的两个变量：

（3）变量的迭代计算过程：

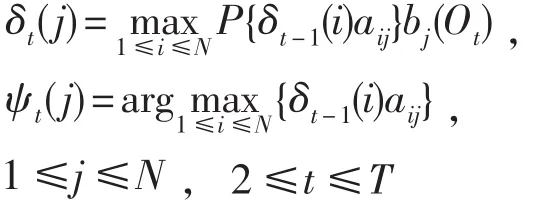
（4）终结迭代过程

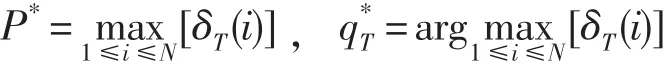
（5）回溯最优路径

由Viterbi过程总结出两大约束条件：

（1）最优路径条件需保证T时刻满足：

（2）最优路径回溯条件应满足：

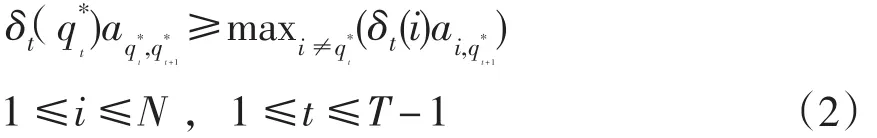
2 逆维特比算法理论框架构建

2.1 逆维特（Inv-Viterbi）比问题的提出

根据维特比问题的定义可以相应地把逆维特比问题[9]描述为：对于给定的HMM模型λ及一状态序列Q，如何确定一观测值序列O，使得所给的状态序列为所求观测值序列的最优状态序列。

2.2 逆维特比算法实现过程

逆维特比问题的提出后，最关键的就是要建立某种算法来实现它，用于解决逆维特比问题的算法称为逆维特比算法。逆维特比算法实现过程是通过对维特比算法实现过程添加某种约束条件及观测值的挑选规则而推导出来的。推导过程定义如下。

（1）定义一个变量Mt(i)，表示的是所给定的最优状态路径上到达t时刻状态为Si的前续路径累积概率，其初始化值定义为：

迭代过程定义为：

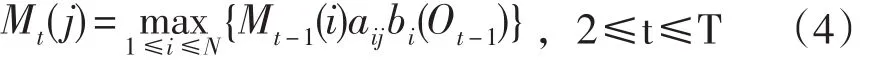
上式中的πi为状态i的初始状态概率，aij表示为状态转移概率，bi(Ot-1)表示的是t-1时刻在状态i观测到观测值Ot-1的概率。

（2）定义约束条件

约束条件一：

约束条件二：

上式中，qt表示的是已经给定了的状态路径Q=q1,q2,…,qT中t时刻的状态。其中不等式（5）和（6）中的约束条件是通过对Viterbi过程的约束条件（1）和（2）分析得来。通过引入这两个约束条件可以确保选取的观测值序列能满足最优路径的要求。由于任意时刻t的观测值Ot都是从观测值空间Vt={v1,v2,…,vM}中选取，为了压缩可能的观测序列搜索空间，提高观测值选取效率，需要进一步提出观测值序列的选择规则。

（3）建立观测值的选择规则

1）筛选规则1：任意时刻t选取的观测值Ot必须要满足约束条件一，若不满足该约束条件的则应该将其从观测值空间中除去，可以进行初步压缩搜索空间；

2）筛选规则2：若在任意时刻t中应用完筛选规则1后观测值空间中剩余的观测值数量还多于一个，则选取剩余观测值中的任意两个观测值v和vˆ，如果选取vˆ为t时刻观测值时，对于t+1时刻任意状态i≠qt+1，由Mt+1(qt+1)-Mt+1(i)所求得的N-1维向量 μ的各个分量均比选取v为t时刻的观测值大或相等时，从观测值空间中去除v，进一步压缩搜索空间。

则逆维特比算法的实现流程如下：

1）初始化初始观测值为O0=ε,ε为一常量；

2）令t=1;

3）应用筛选规则1对t时刻可能取得的观测值进行初步筛选，获得长度为t的观测值序列组Ot=Ot-1Ot，其中Ot（为粗体，表示的是序列）是有t时刻之前的长度为t-1的序列Ot-1增加t时刻的观测值Ot构成的观测值序列，其可能包含多个满足条件的观测值序列；

4）应用筛选规则2对步骤3中剩余的多个观测值序列进行深度筛选，压缩观测值序列组Ot的中观测序列的数量；

5）令t=t+1，若t＜T（T为所给状态序列长度），返回步骤3继续执行，否则往下执行步骤6；

6）运用约束条件二对前面步骤剩下的观测值序列组Ot进行最终的筛选，最后剩下的观测值序列则为逆维特比算法所要求得观测值序列。

3 HMM新评估体系构建

本研究中把逆维特比算法的理论引入到HMM基本算法体系中与维特比算法有效结合，构造一种新的HMM评估体系，如图2所示。

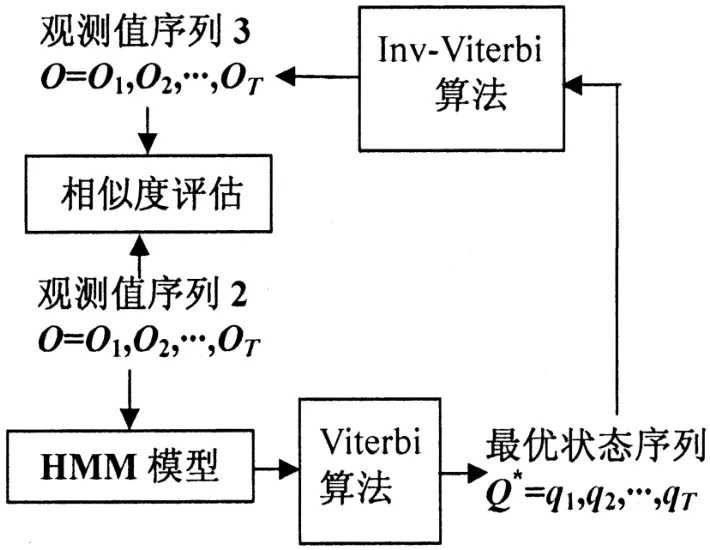
图2 逆维特比闭环评估体系

图2中，通过计算逆维特比算法的输出观测值序列3与维特比算法的输入观测值序列2的相似度来作为HMM模型λ性能的评估标准。

图3 模型与序列关系图

从理论上来说，序列3与序列2应该是相同的序列，但从图3中可以看出，HMM模型参数λ与维特比算法及逆维特比算法的输入及输出序列是密切相关的，因此HMM模型λ性能的好坏将会影响到逆维特比算法的最终输出结果。而在实际的应用中，由于HMM的训练算法自身的不足，最终将会影响其训练结果的可靠性，使训练出来的模型λ难以获得最优性能。因此序列3一般情况下并不是与序列2完全相同的，而且很多时候相差较大，但模型的性能与两观测序列的相似程度存在某种内在的联系，因此可以通过计算两个序列的相似度大小来作为模型性能好坏的量度，而相似度可通过相关系数来衡量。

相关系数的计算式为：

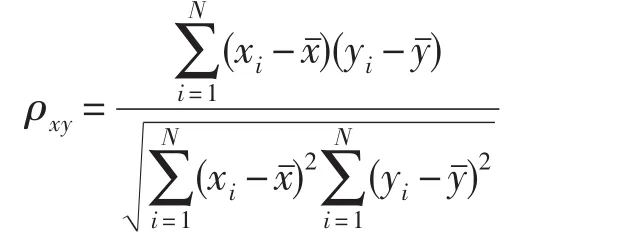
式中，x与y表示的是两个长度为N的序列，x¯与y¯分别表示的是两序列的算术平均值。相关系数的取值范围为0≤|ρxy|≤1，相关系数值越大表明模型性能就越好，反之则性能就越低。

通过引入相似程度的计算，与逆维特比算法及维特比算法一起建立一种HMM模型性能的新评估体系，且这种评估体系为一种闭环的评估体系，对于将评估结果作为训练算法的反馈建立一种闭环训练体系具有一定的指导意义。

4 展望

HMM新评估体系建立后不仅是HMM算法体系的一个补充，而且将对HMM体系的进一步研究提供了新的思路。

（1）HMM循环训练体系。通过新建立的闭环评估体系与HMM训练算法结合，同时引入K-means聚类算法，在模型训练中根据评估结果来评判模型性能的好坏。若训练结果不理想，则通过聚类算法重新优化模型初始值，进入下一次的训练及评估过程，如此，通过训练——评估——再训练——再评估过程建立起一种HMM闭环训练体系。

（2）新型HMM训练算法。逆维特比算法的实现将对HMM其它新算法及理论的研究提供一定的参考价值与指导意义。由图3可知，HMM模型λ是观测值序O与状态序列Q的连接桥梁，通过Viterbi算法可以实现以观值序列O及HMM模型λ作为输入最终获得状态序列Q，而通过逆维特比算法又可以通过输入状态序列Q及HMM模型λ而获得观测值序列O，那么理论上来说也可以参考维特比及逆维特比算法的实现过程来建立另外一种新的问题和算法来实现输入观测值序列O及状态序列Q最终输出HMM模型λ，从而实现一种新的HMM训练算法。

［1］腾格尔，贺昌政，蒋晓毅.隐马尔可夫模型研究进展及其管理领域应用［J］.软科学，2012，26（2）：122-126.

［2］朱明，郭春生.隐马尔可夫模型及其最新应用与发展［J］.计算机系统应用，2010，19（7）：255-259.

［3］ Bengio S.Multimodal speech processing using asyn⁃chron-ous hidden markov models［J］.Information Fu⁃sion，2004，5（2）：81-89.

［4］Lee J M，Kim S J，Hwang Y，et al.Diagnosis of me⁃chanical fault signals using continuous hidden Markov model［J］.Journal of Sound and Vibration，2004，276（3）：1065-1080.

［5］张春良，岳夏，朱厚耀.基于自评估HMM的离心泵状态识别方法研究［J］.广州大学学报：自然科学版，2010（4）：13-17.

［6］Rabiner L.A tutorial on hidden Markov models and se⁃lect-ed applications in speech recognition［J］.Proceed⁃ings of the IEEE，1989，77（2）：257-286.

［7］Viterbi A.Error bounds for convolutional codes and an as⁃ymptotically optimum decoding algorithm［J］.Infor⁃ma-tion Theory， IEEE Transactions on， 1967， 13（2）：260-269.

［8］Forney Jr G D.The viterbi algorithm［C］.Proceedings of the IEEE，1973，61（3）：268-278.

［9］Schnall-Levin M，Chindelevitch L，Berger B.Inverting the Viterbi algorithm：an abstract framework for struc⁃ture de-sign［C］.//Proceedings of the 25th internation⁃al conferen-ce on Machine learning.ACM， 2008：904-911.

Research on theory of Inv-Viterbi Algorithm Based on the Basic Algorithm System of HMM

LIU Gong-sheng1，ZHANG Chun-liang2，YUE Xia2，ZHU Hou-yao2
（1.School of Mechanical Engineering University of South China，Hengyang421001，China；2.Shool of Mechanical and Electrical Engineering，Guangzhou University，Guangzhou510006，China）

The system of the basic Hidden Markov Model（HMM）algorithm includes the three important algorithms of Baum-Welch algorithm，Forward-Backward algorithm and Viterbi algorithm.The Inv-viterbi problem and its corresponding algorithm is put forward in the paper after the research of the new HMM problem and algorithm.Then a new algorithm system and a new evaluation system are built by introducing the Inv-viterbi algorithm into the HMM basic algorithm system.Finally we give a prospect on the application of the new algorithm system.

Hidden Markov Model；Inv-Viterbi problem；Inv-Viterbi algorithm；evaluation system

TP301.6

：A

：1009－9492(2014)11－0007－04

10.3969/j.issn.1009-9492.2014.11.002

刘功生，男，广西玉林人，硕士研究生。研究领域：信号检测与故障诊断。

张春良，男，1964年生，教授，博士生导师。研究领域：设备状态监测与故障诊断、制造过程自动化、微制造技术、激光加工技术和数控技术等。

(编辑：阮 毅)

*国家自然科学基金（编号：51275099）；广东省自然科学基金（编号：S2012010009505）；广州市羊城学者首席科学家项目（编号：12A006S）；广州市机电设备状态监测与控制重点实验室建设项目（编号：2060402）

2014－05－24