钢吊箱封底混凝土与钢护筒粘结力研究

吴加云 郭红敏

（苏州市市政工程设计院有限责任公司 苏州 215007）

1 封底混凝土与钢护筒粘结机理分析

封底混凝土能够与钢护筒共同工作的原因是由于混凝土与钢护筒之间的粘结作用，这种作用能够使其在连接面上实现剪力传递，从而建立起结构所能承载的工作应力，实现钢吊箱在抽水状态时抵抗浮力以及承受承台浇筑时的冲击力及其重量力。参照相关类似的结构，比如光圆钢筋与混凝土的粘结，钢管与混凝土的粘结以及型钢与混凝土的粘结等，可认为封底混凝土与钢护筒的粘结力也是由3部分组成：

（1）吸附力。吸附力是混凝土中的水泥凝胶体在钢护筒表面产生的化学粘着力。

（2）摩阻力。摩阻力是混凝土收缩时混凝土握裹钢护筒而产生的阻滑作用力。

（3）咬合力。咬合力主要是由于钢护筒表面凹凸不平以及钢护筒表面的构造处理与混凝土之间产生的机械咬合作用力。

尽管认为钢护筒与混凝土的粘结作用主要由吸附力、摩阻力和机械咬合力3部分组成，然而，这3部分在整个粘结过程中分别占多少比重、如何工作、受什么因素影响以及粘结破坏过程和机理是怎样的，这些都需要今后进一步大量的试验研究和分析论证。

2 有限元分析方法

在一定作用力条件下，混凝土与钢护筒之间除了力的传递外，还将会产生相对位移等非连续变形，如相对滑移或开裂，这时它们将不再保持为一个变形连续的整体。直接采用连续体的有限元方法进行求解将会产生较大的误差。为了考虑钢护筒与混凝土之间的粘结滑移性能，求得钢护筒与混凝土之间粘结应力的分布，研究结构破坏形态，必须在钢护筒与混凝土之间插入特殊的连接单元，这种单元在空间有位置而无几何体积，可以方便地插入2种不同材料之间。

笔者认为，由于影响粘结的因素很多，破坏机理相当复杂，量测工作又非常困难，无论是钢筋与混凝土之间的粘结本构关系，还是钢管与混凝土之间的本构关系，目前均没有统一的结论；再者，当今一些得到公认的粘结滑移本构关系表达式也是从试验数据归纳拟合出的粘结滑移曲线。因此盲目采用这些本构关系必然会导致结果偏差很大，甚至会得出错误的结论。本文拟在试验的基础上，得到相关参数，采用非线性弹簧单元combination39，对钢护筒和封底混凝土之间的粘结滑移进行数值模拟，探寻其接触面的应力分布规律以及破坏形态，为今后该领域进一步的试验研究及理论分析提供参考依据。

3 封底混凝土粘结力试验研究

3.1 试验方法及过程

根据苏通大桥工程需要，实施了封底混凝土粘结力试验。该试验按照主墩承台1∶0.15的比例，取其中的一个单元制作模型，对封底混凝土与钢护筒的粘结力进行测试。根据比例，确定本模型为一直径2m、厚1m的C30混凝土块。混凝土内预埋一根直径426mm（外径）的钢管，壁厚10mm，沿钢管长度方向安装3层位移杆，每层均匀安装4根。在钢管顶安装承重梁和油压千斤顶，4台250kN油压千斤顶实行联动，实现集中控制，试验装置见图1，图2。

图1 钢管及位移杆的布置

图2 加压装置

3.2 试验结果

试验结果显示：当布置在第一层位移杆上的千分表发生明显变化时，与千斤顶相连的压力表的读数为70MPa，计算得出其对应的局部平均单位粘结力为1.22MPa；当布置在第三层位移杆上的千分表发生明显变化时，与千斤顶相连的压力表的读数为86MPa，扣除钢管及钢管内混凝土的重量，得出对应的平均单位粘结力为0.63MPa。此时钢管与混凝土间已出现了裂痕，荷载不再增长。认为此时混凝土与钢管间的粘结力已发挥。根据本试验中测试结果，混凝土与钢管间的平均粘结强度可取0.63MPa。在钢护筒和混凝土界面剪力传递过程中，认为界面的粘结力沿钢护筒混凝土界面均匀分布，将试验实测的加载端P－S折算¯τ－ε，界面平均粘结应力应变本构关系见图3。

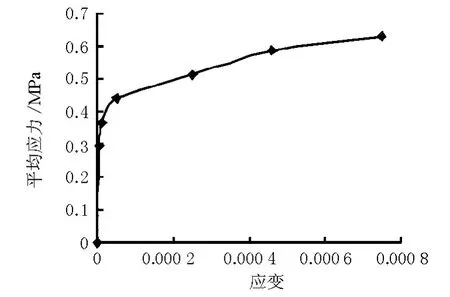
图3 接触面平均应力－应变本构关系

由图3可见，在荷载水平较低时，应变很小，几乎等于0，此时界面吸附力和机械咬合力得到充分发挥；随着荷载进一步增大，曲线斜率递减，应变增长加快，此时摩阻力发挥主要作用；荷载继续增大，靠近加载端的混凝土出现裂痕，此后荷载不再增长，混凝土与钢管间的粘结力已全部发挥。

4 钢护筒与封底混凝土粘结数值模拟

4.1 单元选取

钢护筒及其内浇钢筋混凝土采用块体Sol－id45等参单元模拟；封底混凝土采用块体Solid65等参单元模拟；为了模拟封底混凝土与钢护筒之间的应力分布规律及其破坏形态，必须考虑两者之间的粘结滑移。本文采用非线性弹簧单元combination39来模拟。

4.2 材料特性

（1）钢材Solid45单元参数。在材料非线性分析中，采用目前常用的随动强化准则，钢材的本构关系取单调的二折线弹性强化模型，即钢材屈服后的应力－应变关系简化为平缓的斜直线，见图4。初始弹性模量取Es＝210GPa，进入塑性强化阶段切线模量可取E′s＝0.01 Es，屈服强度fy＝235MPa，质量密度ρ＝7 850kg／m3，泊松比v＝0.3。

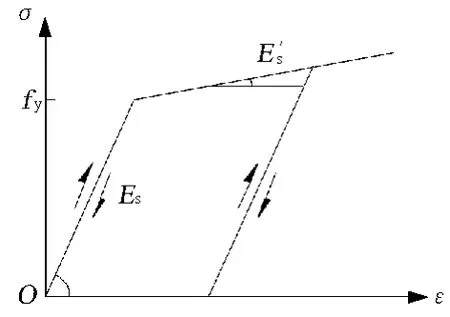
图4 钢材线弹性强化本构关系

（2）混凝土Solid65单元参数。封底混凝土采用多线性随动强化模型，其本构关系采用混凝土受压等效单轴应力应变Hognestad模型，如下式所示。

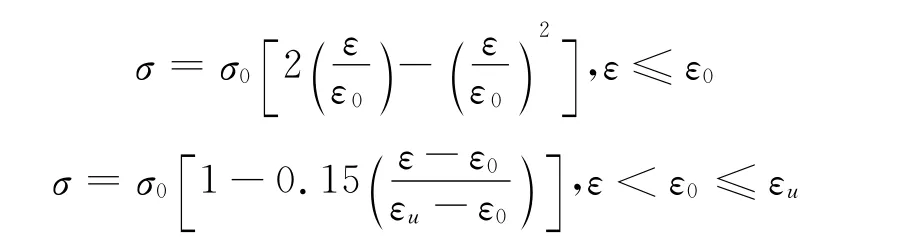
表1 C30混凝土计算参数

（3）弹簧单元参数。钢护筒与混凝土之间的粘结滑移通过3个单向弹簧来模拟，分别为法向（垂直接触面方向）、横切向（平行接触面且垂直接触长度方向）、纵切向（平行接触面和接触长度方向）。见图5，图6。

纵切向：该方向是钢护筒与混凝土之间的粘结滑移主要研究的内容，由试验结果的平均粘结应力－应变本构关系，根据下式可得到每根弹簧的F－D 曲线。

图5 法向力－变形曲线

图6 横切向力－变形曲线图

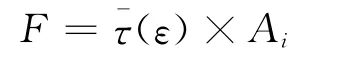
式中：Ai为第i根弹簧所占界面的面积，具体计算见图7，图8。

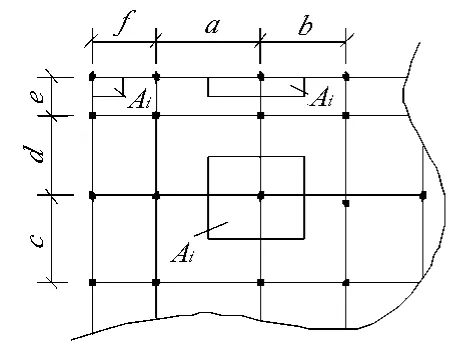
图7 不规则网格Ai计算

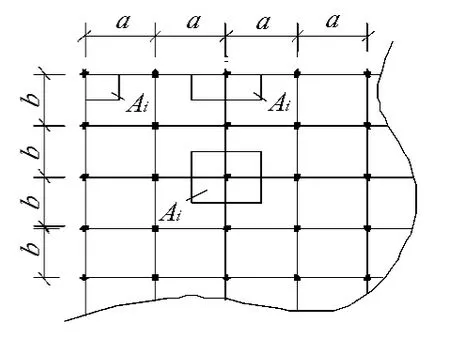
图8 规则网格Ai计算

根据弹簧所在位置，可分为角部弹簧、边界弹簧和中间弹簧3种，其对应的面积计算公式如下：

4.3 计算模型

（1）建模及单元划分。本文研究的对象是封底混凝土试验模型，由于加载及边界的轴对称性，故可取1／4模型来计算。对角部弹簧、边界弹簧和中间弹簧分别采用3个不同的实常数进行区分，见图9。单元类型及实常数见表2。整体有限元模型见图10。

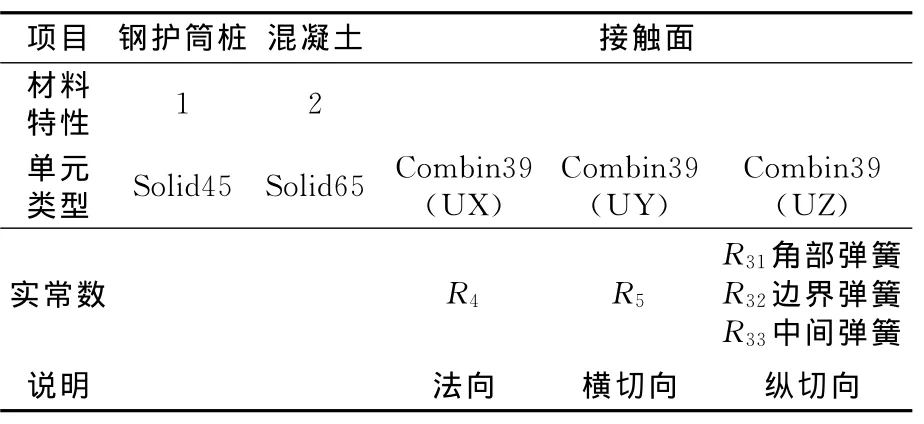
表2 单元类型及实常数

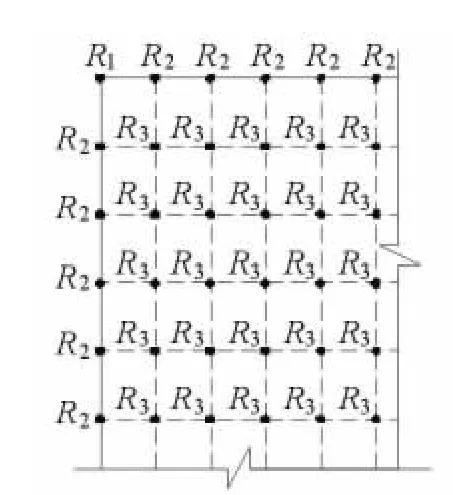
图9 不同的实常数分布

图10 整体有限元模型

（2）屈服及失效准则。Solid65可以预测混凝土的失效行为，可以同时考虑开裂和压碎失效模拟，多轴应力状态下混凝土失效准则表达式如下：

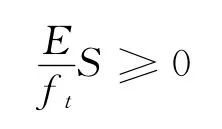
式中：F为主应力的函数；ft为混凝土单轴抗拉强度；S为失效面。

4.4 结果及分析

根据前面对钢护筒和混凝土接触面粘结的试验和理论分析，按位移加载方式进行加载，设置100个荷载子步，打开线性搜索，用 Newton－Raphson增量迭代法求解，得出粘结滑移的基本分布规律见图11～17。

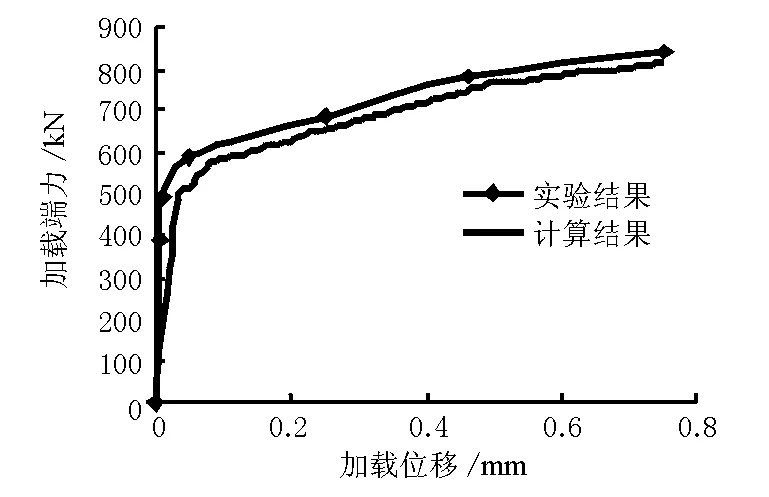
图11 加载端力和位移（P－S）曲线比较

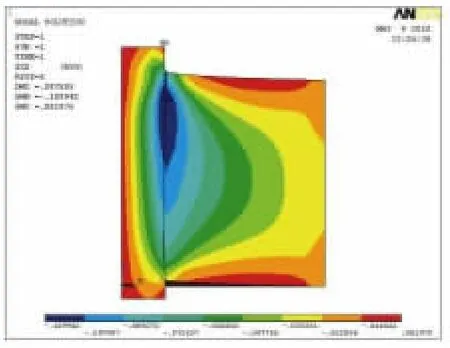
图12 初始加载剪切应力等值线

图13 滑移前剪应力等值线

图14 位移等值线图

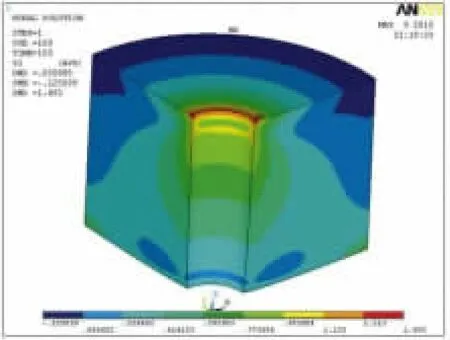
图15 混凝土第一主拉应力等值线图

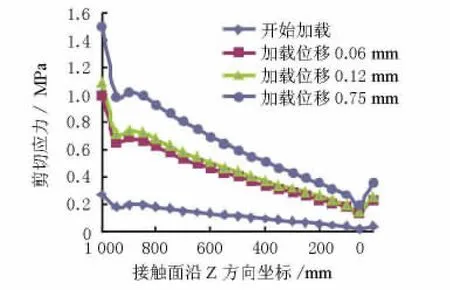
图16 接触面剪切应力随位置和荷载变化图

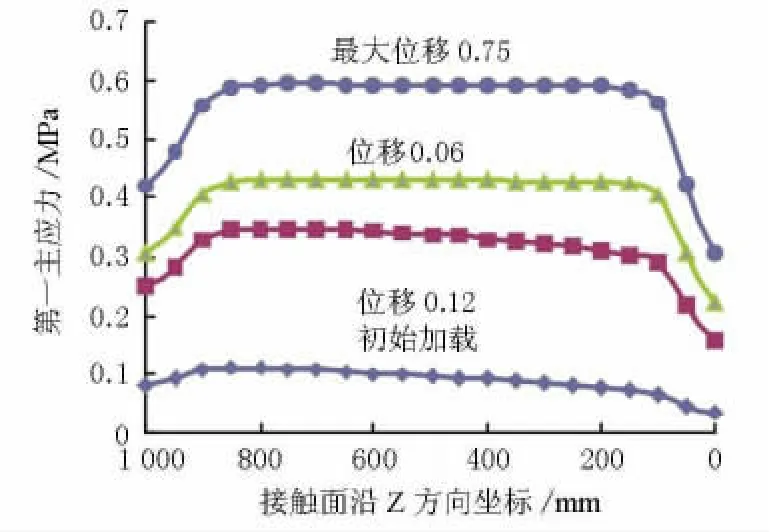
图17 混凝土第一主应力随位置和荷载变化图

图11所示的计算曲线与试验曲线吻合较好，今后可以采用非线性弹簧单元模型对钢护筒与混凝土之间界面粘结滑移的内力分布进行计算分析。在各个加载阶段，界面剪切应力的分布情况由图12、图13、图16，以及界面混凝土的主拉应力分布情况由图15、图17可见：

（1）在初始加载阶段，剪切应力分布比较集中，主要分布在靠近加载段一侧，此时，力的作用尚未完全传递到自由端，因而自由端的剪切应力相对较小，与试验现象相符。

（2）随着荷载的增加，剪切应力不断增大，且快速向自由端推进，但靠近自由端一侧，剪切应力值较小；荷载加大到极限荷载时，钢护筒与混凝土之间产生滑移，剪切应力达到最大值，且完全推进至靠近自由端，此时，剪切应力沿埋置长度均匀分布。

（3）混凝土第一主拉应力，除靠近加载端和自由端的分布比较复杂外，中间段沿埋置长度方向在加载过程中趋于直线分布。在整个加载过程中，主拉应力水平较低，在混凝土顶端达到最大，该位置将最先产生裂缝，与试验现象相符。

（4）由图17不同荷载作用下的拉应力曲线斜率发展规律可以看出，随着荷载的增加，混凝土主拉应力不断增大，靠近加载端的拉应力增大幅度大于自由端，且随着荷载的增大，幅度增长速度加快。

5 结论

（1）使用Newton－Raphson增量迭代法求解非线性问题时，打开线性搜索、自动时间步长等功能可加速收敛。按位移加载方式比力加载方式更具有优势，设置100个荷载子步，可满足要求。

（2）计算结果与试验结果吻合较好，今后可以采用非线性弹簧单元模型对钢护筒与混凝土之间的界面粘结滑移的内力分布进行计算分析。

（3）在初始加载阶段，剪切应力分布比较集中，主要分布在靠近加载端一侧，此时，力的作用尚未完全传递到自由端，自由端的剪切应力相对较小，随着荷载的增加，剪切应力不断增大，且快速向自由端推进，但靠近自由端一侧，剪切应力值较小；荷载加大到极限荷载时，钢护筒与混凝土之间产生滑移，剪切应力达到最大值，且完全推进至靠近自由端，此时，剪切应力沿埋置长度均匀分布。

（4）混凝土第一主拉应力，除靠近加载端和自由端的分布比较复杂外，中间段沿埋置长度方向在加载过程中趋于直线分布。在整个加载过程中，主拉应力水平较低，在混凝土顶端达到最大，该位置将最先产生裂缝。靠近加载端的拉应力增大幅度大于自由端，且随着荷载的增大，幅度增长速度加快。

［1］ 牟晓光.高强预应力钢筋粘结性能试验研究及数值模拟［D］.大连：大连理工大学，2005.

［2］ 过镇海，时旭东.钢筋混凝土原理及分析［M］.北京：清华大学出版社，2003.

［3］ 薛立红，蔡绍怀.钢管混凝土柱组合截面的粘结强度［J］.建筑科学，1996（3）：22－28.

［4］ ROEDER C W，CAMERON B，BROWN C B.Composite action in concrete filled tubes［J］.Journal of Structural EngineerIng，ASCE，1999，125（5）：477－484.

［5］ JOHANSSON M，GYLLTOFT K.Mechanical behavior of circular steel－concrete composite stub columns［J］.Journal of Structural Engineer，2002，74（13）：1073－1081.