一种工业机器人切削加工的系统集成与仿真方法
刘祥 陈友东 王田苗
(北京航空航天大学机器人研究所,北京,100191)
一种工业机器人切削加工的系统集成与仿真方法
刘祥 陈友东 王田苗
(北京航空航天大学机器人研究所,北京,100191)
本文以QH165工业机器人为例,提出了利用6R工业机器人与CAD/CAM系统集成的切削加工解决方案,论述了切削加工机器人与CAD/CAM系统集成化,包括在SolidWorks软件中CAD建模和在MasterCAM软件中选取五轴数控机床进行CAM加工;并针对该切削加工系统,重点推导后置处理过程中机器人运动学正逆解和轨迹优化算法,在Unity3D引擎中建立仿真平台,模拟仿真机器人运动。实验结果验证了该系统设计和轨迹优化算法的正确性。
机器人,切削加工,CAD/CAM,后置处理,Unity3D
0 引言
工业机器人在工业自动化领域已经得到了广泛的应用。在切削加工领域,工业机器人由于刚度和精度不足,导致其发展和应用受限,但是在一些低精度、低切削力要求的复杂曲面加工领域(如木材雕刻加工),作为一种相比于高价格数控机床有显著成本优势的替代方案,仍具有良好的发展前景。因此,使用工业机器人作为一种高性价比的切削加工平台,逐渐成为工业机器人一个重要的、快速发展的方向。
当前,国内外有关工业机器人进行切削加工的研究正在成为热点之一。2012年,Javier Andres和Luis Gracia等领导研究小组开展了冗余工作空间下机器人切削加工后置处理模块的研究,针对其轨迹优化算法进行仿真试验,提出了切削加工系统解决方案[1-2]。同年,Ji Xiang等人研究了在7自由度工业机器人条件下,利用多重阻尼因子回避优化轨迹运动时的奇异点问题[3]。2011年,北京航空航天大学肖文磊等人研究了冗余自由度条件下奇异点规避优化算法等问题[4]。但是,对于已有的加工机器人研究和应用,利用雅克比矩阵第二条件数来达到更高效的轨迹优化算法则很少讨论,而该问题对解决机器人后置处理轨迹优化有重要意义。
本文围绕机器人轨迹奇异点回避等难点,利用QH165工业机器人建立了一套实用的切削加工机器人系统。首先,使用SolidWorks和MasterCAM作为CAD和CAM系统模块,生成G代码,其次,构建后置处理器模块,提出了更高效的轨迹优化算法,将G代码转换为自定义的机器人中间语言,最后在Unity3D引擎中建立仿真平台,并简单模拟了工业机器人运动过程。该解决方案能够针对不同的机器人结构方便实现轨迹优化。
1 系统总体结构
1.1系统框架
在传统的数控加工领域,主要使用CAD-CAM-CNC数据链完成复杂工件的加工。本文借助传统的数据链加工模型,建立基于CAD-CAM-Unity3D加工机器人系统数据链仿真系统模型,系统流程图如图1所示。
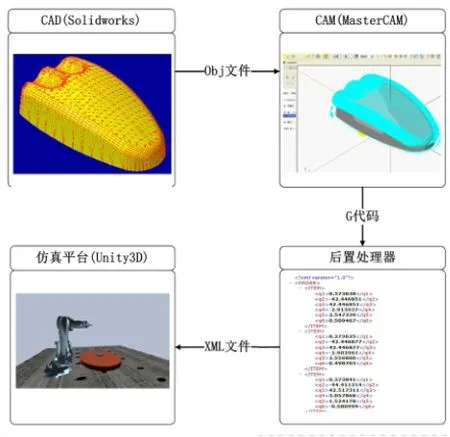
图1 加工机器人系统流程图
在构建的机器人切削加工系统中,首先,使用SolidWorks进行工件建模,将CAD模型进行文件转换后导入到MasterCAM软件中进行毛坯定义、刀具选取、加工路径选取和加工轨迹生成等工作;然后将输出的G代码文件导入到后置处理器中,进行数值提取、坐标系转换及轨迹优化,将优化后的关节速度值保存为XML文件并输出;最后将输出的XML文件导入到Unity3D仿真平台进行机器人运动仿真。
1.2后置处理模块
与传统CAD-CAM-CNC数据链相比,切削加工机器人最大的不同之处是加入了后置处理器模块。切削加工机器人的后置处理过程及组成模块如图2所示。
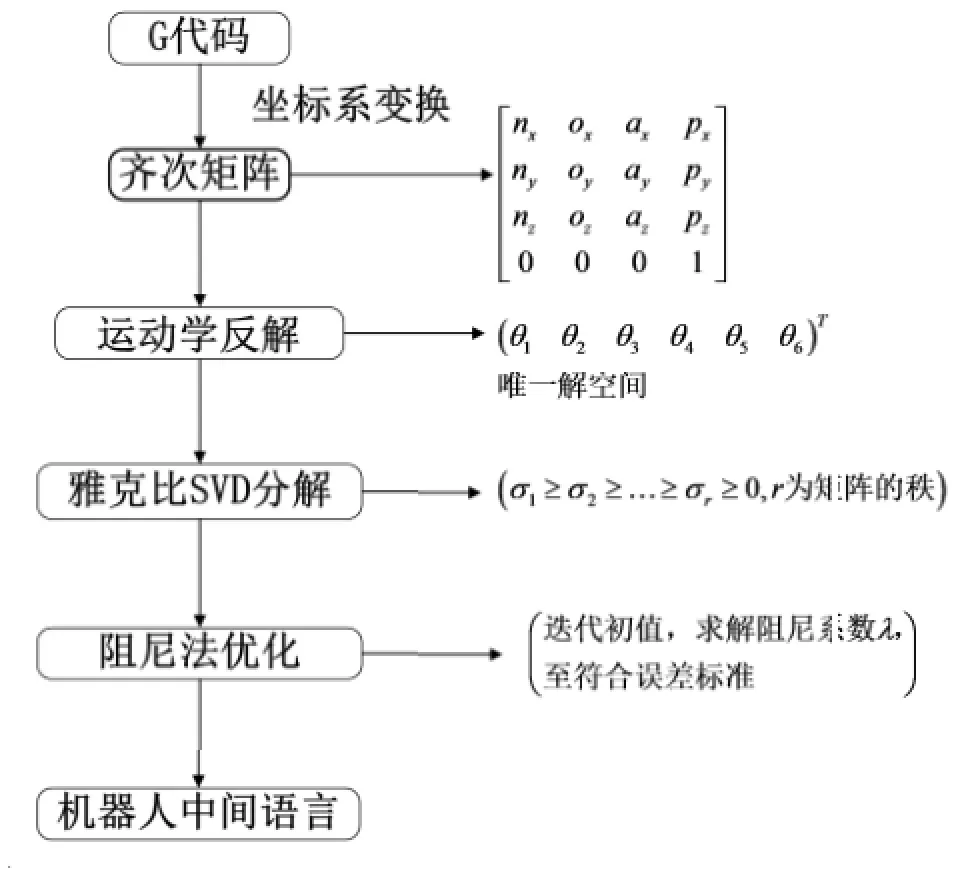
图2 切削加工机器人后置处理流程图
本文重点研究五坐标机床的G代码,机器人利用齐次矩阵表示末端执行器的坐标和方向,需要把G代码转换为机器人坐标系下的位姿矩阵。
由于需要对机器人运动轨迹进行优化,故而需要先对机器人建模和运动学正反解,得出约束条件下唯一解空间。
利用阻尼系数法进行轨迹优化,必须先求解机器人的雅克比矩阵并对其进行奇异值分解。
不同的机器人语言也不同,为了增强普遍性和提高适用性,生成得出自定义的机器人语言格式,并利用XML语言保存生成的文件。
2 机器人运动学模型
2.1运动学正解算法
切削加工机器人QH165的实体图如图3所示。QH165是一个典型的6R机器人(具有6个旋转自由度的串联机器人),对于五坐标数控代码具有1个冗余自由度。

图3 QH165机器人
D-H法(Denavit-Hartenberg)是机器人常用的建模方法,可用于机器人正运动学解算、3D模型运算。利用D-H法可以很方便地建立串联机器人的连杆坐标系和变换矩阵。图4为使用D-H法构建的QH165机器人坐标系建模图,表1为各连接轴的D-H参数。
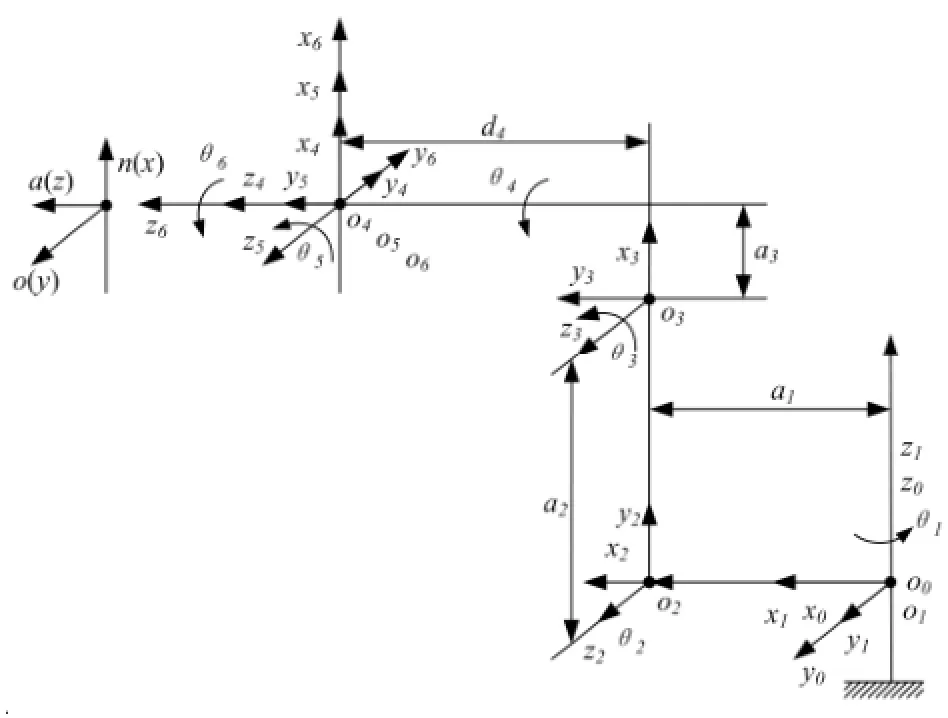
图4 QH165机器人坐标系建模
建立为世界坐标系,为各个关节坐标系,为各个关节绕其Z轴旋转角度。
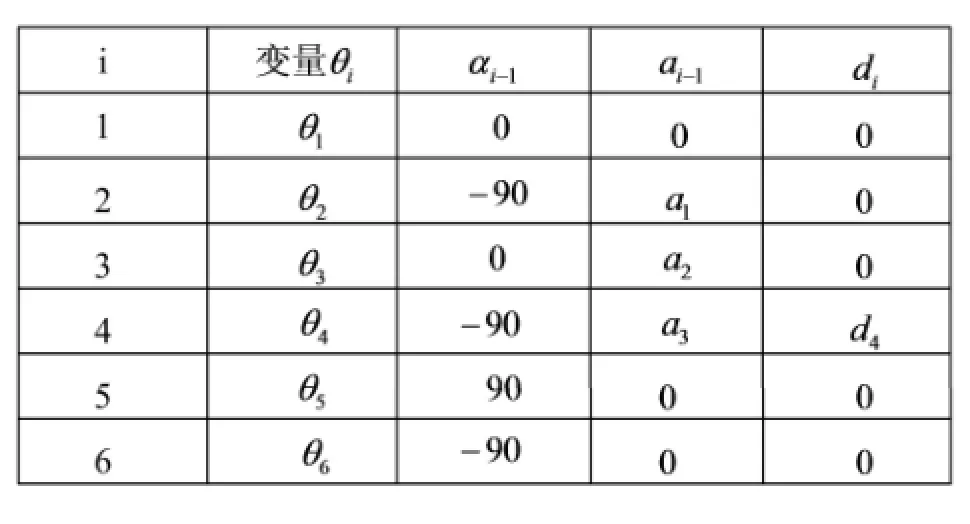
表1 QH165机器人的D-H参数
根据D-H参数表,计算各个关节运动学方程,再根据公式(1)计算机器人运动学方程:
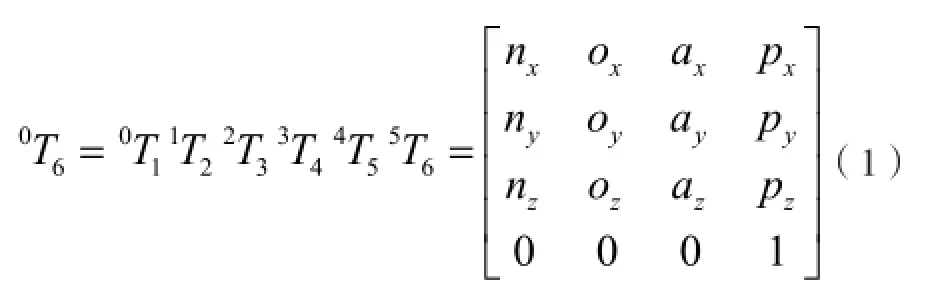
利用Matlab软件计算矩阵中各个元素的表达式。
2.2运动学逆解算法
一般情况下,除了一些特例,超过5自由度的工业机器人都不存在逆运动学方程的封闭解。而对于QH165机器人而言,由于其最后3个关节轴线交于一点,属于存在解析解的特例。这里将6个旋转轴划分为和两组分别求解。
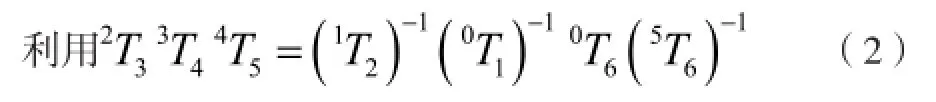
计算可简单得到:
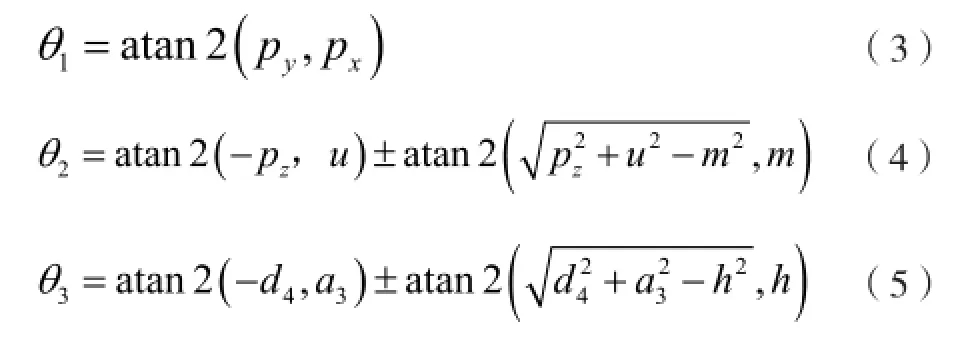
式中,
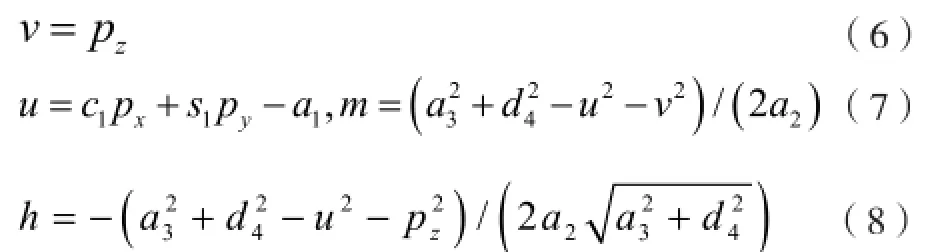
同理可得:
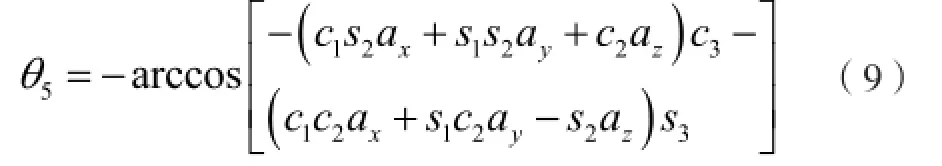
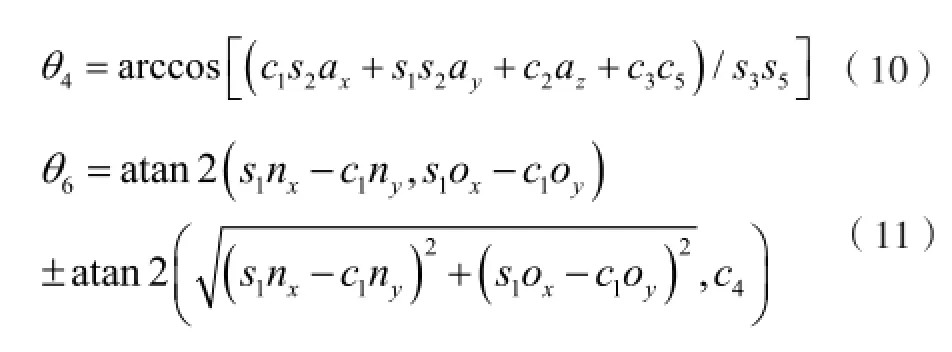
3 运动轨迹优化
机械手的操作速度与关节速度的线性变换定义为机械手的雅克比矩阵,可视它为从关节空间向操作空间运动速度的传动比。将机器人运动学方程两边对时间求导,得出:

其中,为末端在操作空间的广义速度,简称操作速度;为关节速度;为机械手的雅克比矩阵。
根据微分运动知识,将式(12)中的积分换为微分量,得到:
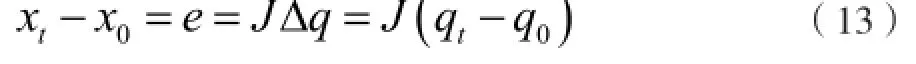
其中,为关节变量增量,为末端位姿误差矢量。根据最小二乘的原理,由下式求解得出。

当机器人处于奇异位姿时,雅可比矩阵奇异,表现为机器人失去某些操作空间自由度,在奇异点附近,实现较小的末端速度也需要极大的关节速度。常用的奇异点处理方法是在奇异点附近引入速度阻尼项,在跟踪精度和关节速度之间寻找一个平衡点,即
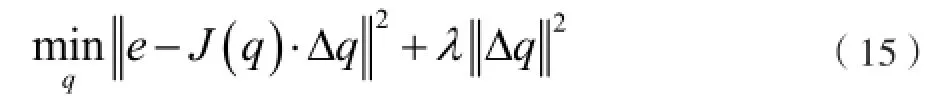
上式的解可表示如下:
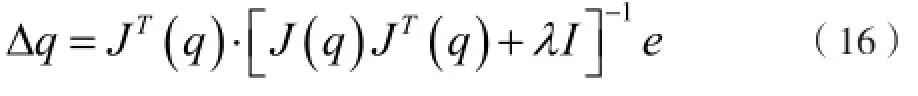
其中为单位矩阵,阻尼项的引入可保证在奇异点附近伪逆解的稳定性,但这要以牺牲关节速度的精确性为代价,因此,在保证伪逆解稳定的前提下,要尽可能提高关节速度的精度,则有必要在计算过程中对阻尼项系数进行自适应调整。
使用雅克比奇异值分解:

得到:
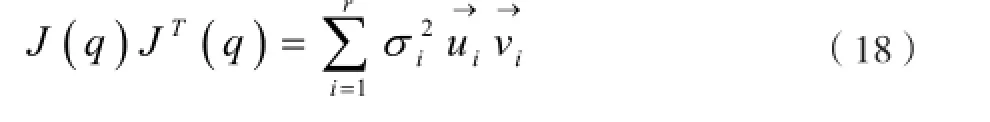
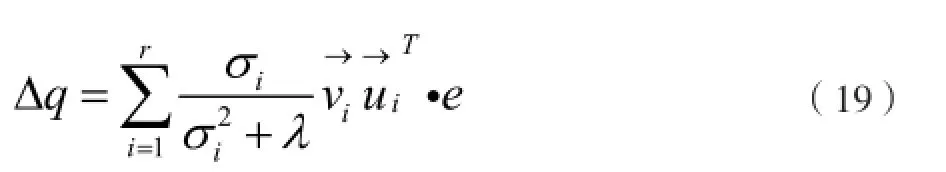
其中,雅克比矩阵的条件数可以反映机器人接近奇异位姿的程度,条件数表示如下:

通过雅克比矩阵结构分析,提出另外一个奇异性指标:第二条件数k2。由于机器人处于不同位姿时关节速度变化较大,第二条件数能够在一定程度上反映机器人的各项同性性质及奇异性。第二条件数弥补了条件数k1对奇异性表示的不全面性,继而基于k2提出了一种新的阻尼系数自适应调整方法,增强了逆解算法的奇异鲁棒性。
因此,在奇异点附近,考虑条件数k1的同时加入第二条件数k2,当k2较大时,同样添加阻尼项,以保证算法的稳定性。按式(21)调整阻尼因子,其中为阈值。
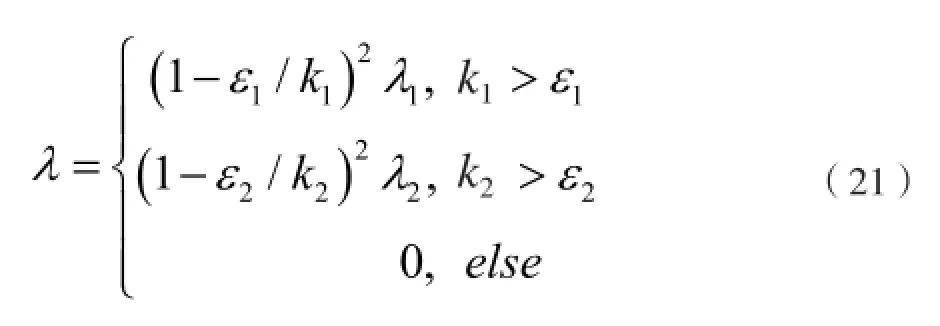
针对机器人模型,轨迹优化迭代算法流程如图5所示。
4 运动轨迹仿真
机器人运动仿真界面如图6所示。采用Unity3D引擎平台实现机器人系统仿真运动,利用Unity3D编辑器和MonoDevelop开发环境进行资源加载、场景搭建和控制编程。在该仿真平台上,编写XML读取与解析模块,以便读取上文描述的G代码经过轨迹优化后保存的XML文件。最后,依据每一时刻各个关节的运动转角实现机器人编程和运动仿真,经过运动仿真验证该系统设计的合理性和轨迹优化算法的正确性。

图5 机器人运动轨迹优化算法流程图

图6 机器人运动仿真界面
5 结论
本文针对切削加工的需求,设计工业机器人切削加工系统,实现了该系统建模与仿真,并测试了该机器人系统轨迹优化算法的实用性和稳定性。
[1] Andres J, Gracia L, Tornero J. Implementation and testing of a CAM post processor for an industrial redundant workcell with evaluation of several fuzzified Redundancy Resolution Schemes[J].Robotics and Computer Integrated Manufacturing,2011,28(2):265-274.
[2] Andres J, Gracia L, Tornero J. Calibration and control of a redundant robotic workcell for miling tasks[J].International Journal of Computer Integrated Manufacturing,2011,24(6):561-573.
[3] Xiang Ji, Zhong Congwei,Wei Wei.Avaried weights method for the kinematic control of redundant manipulators with multiple constraints[J].IEEE Transactions on robotics,2012,28(2).
[4]肖文磊,郇极.切削加工机器人与CAD/CAM系统集成化[J].机械工程学报,2011,47(15).

