铝矿资源海外开发战略选区政治风险评价

袁纬芳，郑明贵，陈家愿

铝矿资源海外开发战略选区政治风险评价

袁纬芳，郑明贵，陈家愿

（江西理工大学经济管理学院，江西赣州341000）

传统的政治风险评价只考虑诸如政治、政策法律法规的风险，但海外开发铝矿资源的政治风险复杂、易变，除受政治影响外，还受该国经济和社会风险的影响。文章首先对铝矿资源海外开发战略选区政治风险因素进行识别；采用粗糙集理论对指标进行赋权，并利用粗糙集对指标进行约简，最后结合灰色关联评价法对战略选区的政治风险进行评价，得出战略选区政治风险大小的排序。结果表明：澳大利亚、美国、巴西等国的政治风险较低，印度、希腊等国的政治风险较高。>

铝矿；政治风险；粗糙集；灰色关联法

我国铝土资源虽比较丰富，但一方面我国铝土矿质量较差，其中耗能大的一水硬铝石型矿石占全国总储量的98%以上；另一方面，大规模的工业化使我国铝矿资源的供应有较大部分来自进口。因此，合理开发并利用海外铝矿资源是保持我国经济持续增长的有效保障，但进行海外铝矿资源的开发所面临的不确定性因素较多，而且政治环境如何是决定项目能否取得预期收益的关键性因素，对铝矿资源海外开发战略选区政治风险的评价对企业具有重大意义。

总结国内外学者对政治风险的研究，发现政治风险主要是由东道国的政治、经济及社会的变化所引发的：政治层面的风险主要由东道国的政治事件或政策变化所引发；经济层面风险主要受东道国的宏观经济情况和物价水平影响；社会层面的风险主要在于东道国的社会是否安定，其可能造成小范围的罢工、游行，大范围的暴乱甚至政局动荡。

一、风险因素识别

（一）铝矿资源海外开发战略选区

本文选取了13个铝矿资源相对丰富的国家作为我国铝矿海外开发的战略选区，包括澳大利亚、几内亚、巴西、印度等国家。13个战略选区的铝矿资源储量情况如表1所示[1-2]。

表1 世界铝矿资源储量情况

（二）政治风险指标的构建

政治风险是海外矿业投资项目评估的起点，是决定该项目能否成功的关键因素，由于其复杂性、易变性和诱发因素的多样性等性质，导致对政治风险的防范与控制难度很大。可以看出，虽然政治风险受突发因素的影响很大，突发的战争、灾害、内乱等会使一国的政治风险迅速升高，但这些突发因素往往是无法预测的，一国的政治风险更多的是受该国的政治、经济和社会等多个层面所带来的风险所影响[3～4]。因此，本文将从通过一系列的政治、经济及社会层面的指标来评价铝矿资源战略选区的政治风险情况，根据这三个层面建立的铝矿资源战略选区政治风险评价指标体系如表2所示。

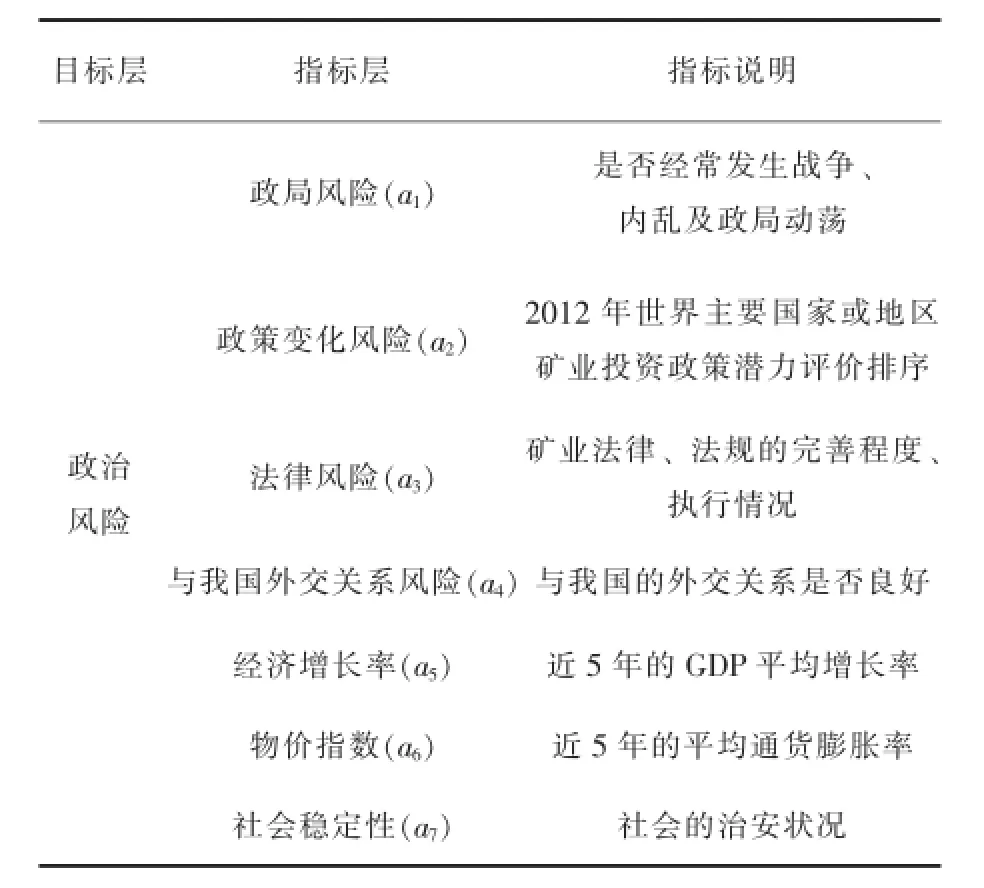
表2 铝矿资源战略选区政治风险评价指标体系

二、基于粗糙集理论的指标权重的确定

（一）粗糙集理论基本原理

粗糙集理论的基本思想是在保持信息系统的分类能力不变的基础上，通过知识约简形成概念或分类规则[5]，其特点是不需提供除问题所需的数据集合之外的任何先验信息，对问题的不确定的描述和处理相对客观[6]。在对铝矿资源战略选区政治风险评价时，如果通过专家对各项指标赋权，那么大量不确定信息的存在会影响评价结果的准确性，因此就比较适合运用粗糙集相关知识对政治风险评价指标进行赋权。

1.信息系统

粗糙集理论中，由信息系统来实现知识的表达，再通过知识将对象进行分类。信息系统是以4元组S=（U，A，V，f）来表示[7]，其中U表示对象的非空有限集合，U=（x1，x2，…，xn），称为论域；A表示非空有限集合，也即评价指标属性集，其中A=（a1，a2，…，am），A中的每个aj（j≤m）称为一个属性，V＝∪Va，Va是属性的值域，a（x）是对象x的属性在a上的值；f∶U×A→V是一个信息函数，它为每个对象的每个属性赋予一个信息值，即Aa∈A，x∈U，

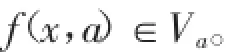
2.可辨识矩阵

可辨识矩阵为信息系统中当决策属性不同且条件属性也不完全相同时，元素值为互不相同的属性组合[8]。当决策属性完全相同时，元素值为0；当决策属性不同、而条件完全相同时，元素值为-1，则表明系统中数据有误或提供条件属性不足。设S=（U，A，V，f）是一个信息系统PA，U/ind（P）=（x1，x2，…，xn），则可辨识矩阵记为[9]：

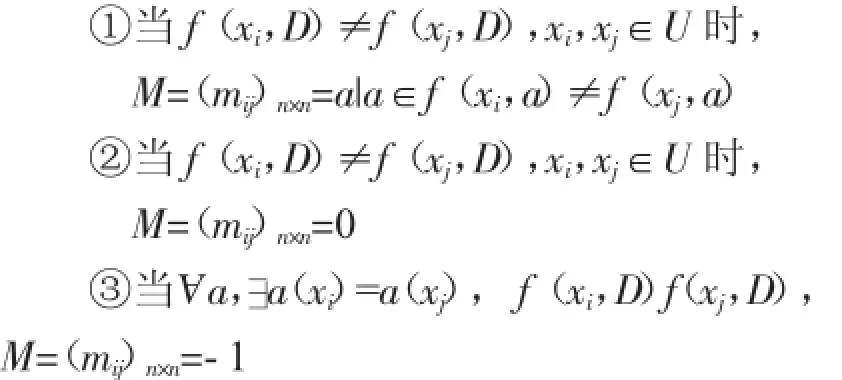
3.属性重要性重量

对于一个可辨识矩阵M=（mij）n×n，属性a∈A在A中的重要定义为：

通过可辨识矩阵可以看出，表明属性a∈A在A中的重要性是由A中去掉{a}后所引起的信息量变化的大小来度量的。可辨识矩阵中某项的长度越短，该项对分类所起的作用就越大，且该项出现的越频繁，该项就越重要。因此，属性在可辨识矩阵中出现的次数越多，出现的项越短，则属性的重要度越大。

4.属性约简

属性约简又称只是约简，是在保持知识库分类能力不变的条件下，删除不相关或不重要的知识[10]。

（二）指标权重的确定

1.原始数据

按照铝矿资源战略选区政治风险评价指标体系，即A={a1,a2,a3,a4,a5,a6,a7}，选取13铝矿资源丰富的国家作为评价对象，即U={X1,X2,X3,X4,X5,X6,X7, X8,X9,X10,X11,X12,X13}。13个待评价国家的政治风险情况如表2所示。

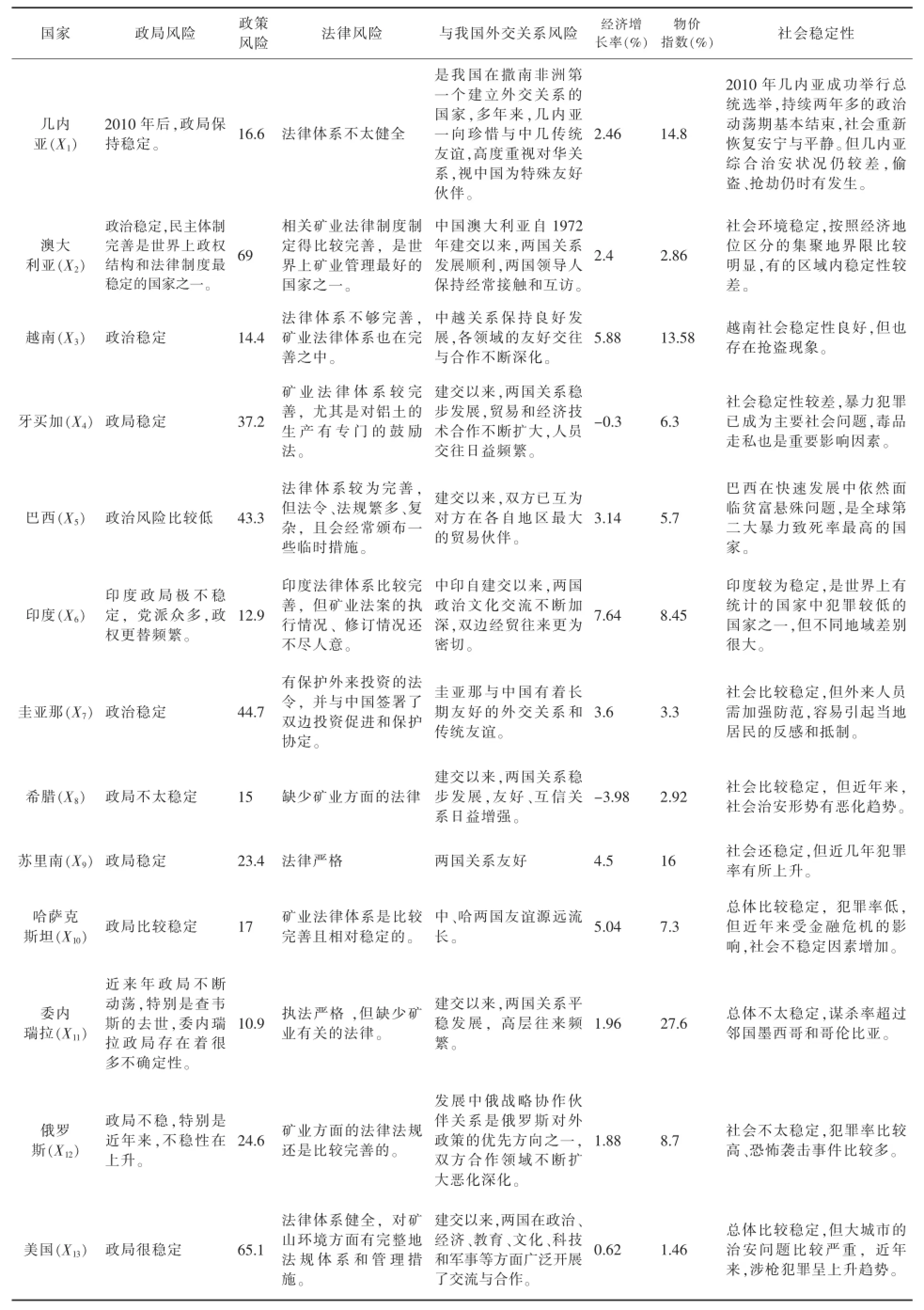
表2 13个国家的政治风险情况

2.评价指标分级

为将各国家的政治风险进行量化，需对政治风险评价指标进行分级，具体分级规则如表3所示。

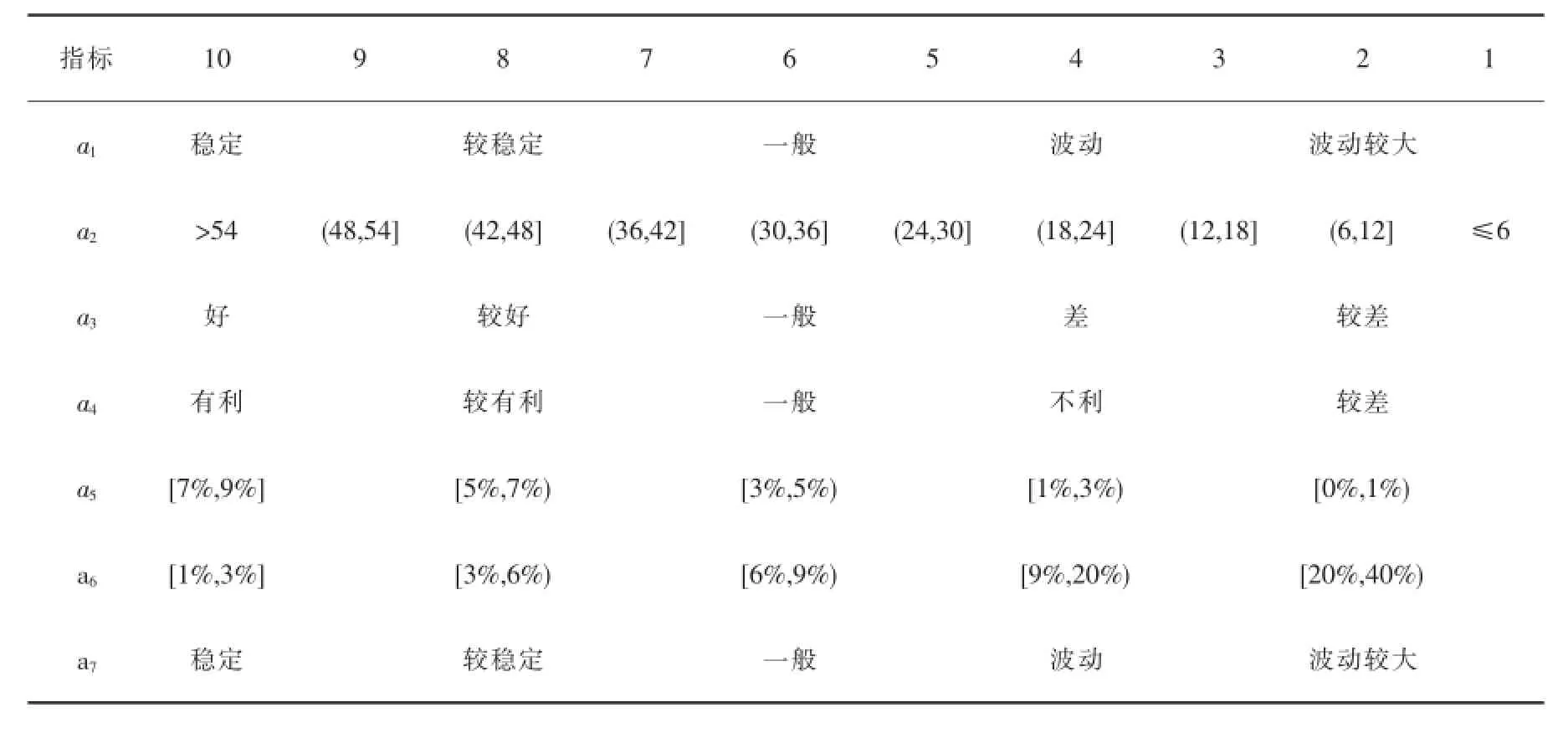
表3 评价指标分级规则

根据表3的分级规则，结合表2中各个国家的政治风险情况确定各指标的分级值。结果如表4所示。

表4 13个国家的政治风险指标值

3.计算可辨识矩阵

根据表4中所得出的风险指标值，因为没有给出决策属性信息，则认为该信息系统中所有决策属性不同，因此按照可辨识矩阵的规则计算出知识信息系统的可辨识矩阵如表5所示。

表5 可辨识矩阵

基于可辨识矩阵的启发式算法，按公式（1）计算知识系统7个属性（评价指标）的重要度，分别为：f（a1）=12.07；f（a2）=11；f（a3）=11.93;f（a4）=8.36；f（a5）=11.83；f（a6）=12.12；f（a7）=10.83

通过上式求解，得到各属性重要度的排序为：

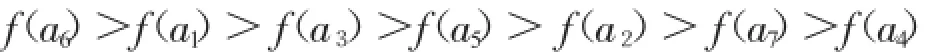
4.属性约简

属性约简是在保持知识库分类能力不变的条件下，删除不相关或不重要的知识，根据上述重要度的计算，a4的重要度最小，a4是各国“与我国外交关系这一指标”，从表3可看出，各指标值相差不大，说明各国家与我国的外交关系大同小异，因此约掉a4这一指标。

5.重要度计算

对约简后的指标进行归一化，算出各指标的权重值为：

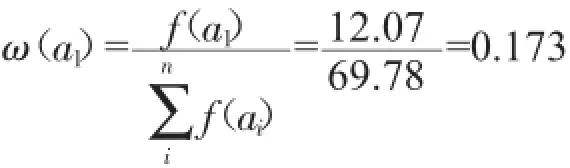
同理计算出：

三、建立灰色关联评价模型

（一）灰色关联评价模型基本原理

灰色系统评价的基本思路是，根据各个比较数列集构成的曲线族，和参考数列构成的曲线间的几何相似程度确定比较数列集与参考数列间的关联度，两者曲线的形状越相似，其关联度就越大[11]。对于铝矿资源海外开发战略选区政治风险灰色系统评价问题，每个国家的所有指标值就构成了一个比较数列，记为：

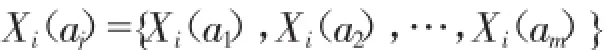
其中，i=1，2，…，n表示国家的个数；j=1，2，…，m表示每个国家的指标数。

1.确定参考数列

在对各个国家进行评价时，首先要制定评价标准，采用灰色关联分析法进行评价，则评价标准就是各指标中的最优值[12]。本文在对指标进行分级时规定分值越高，即表明该国家最优，即风险越低。因此，参考数列记为：

2.计算综合评价的关联度

根据灰色系统理论[13]，定义比较数列Xi对参考数列X0在指标Xi（aj）上的关联系数为：

其中ρ为分辨系数，通常取为0.5。

最后综合评价关联度的计算式为：

（二）铝矿资源海外开发战略选区政治风险灰色关联评价模型

按照灰色关联系统，对铝矿资源海外开发战略选区政治风险灰色关联评价如下：

在属性约简后，根据表4中13个国家政治风险指标值可将参考数列确定为：

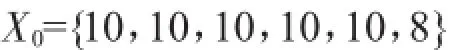
根据公式（2）计算出每个比较数列对参考数列在各个指标上的关联系数为：

ξ1（aj）={0.692，0.429，0.529，0.474，0.474，1}

ξ2（aj）={1，1，1，0.333，1，1}

ξ3（aj）={0.636，0.333，0.467，1，0.368，1}

ξ4（aj）={1，0.75，1，0.5，0.75，0.857}

ξ5（aj）={0.818，1，0.818，0.818，0.818，0.6}

ξ6（aj）={0.333，0.333，0.467，1，0.412，0.636}

ξ7（aj）={0.5，0.5，0.5，0.333，0.5，1}

ξ8（aj）={0.306，0.175，0.204，0.136，1.222，1.222}

ξ9（aj）={1，0.444，0.444，0.571，0.444，1}

ξ10（aj）={0.538，0.333，0.636，0.538，0.467，1}

ξ11（aj）={0.636，0.538，0.778，0.7，0.583，1}

ξ12（aj）={0.556，0.625，0.833，0.556，0.714，1}

ξ13（aj）={0.8，1，0.8，0.333，1，1}

最后根据公式（3）计算出每个国家的总体关联度及排名如表6所示。

表6 铝矿资源海外开发战略选区政治风险灰色关联评价

由上表可知，印度的风险最高，主要原因还是在于政局不稳定；排在第四位的哈萨克斯坦虽然政局比较稳定，但其矿业投资政策潜力评分过低，因此也存在较高的风险；风险最低的澳大利亚，不仅政局稳定、政策潜力高、经济稳定，社会也很稳定，是开发铝矿资源的首选国家；排在第四位的牙买加和第五位的俄罗斯关联度相差比较大，原因在于牙买加的政局远比俄罗斯稳定。

四、结论

1.将13个铝矿资源储备丰富的国家进行政治风险评价。

2.对政治风险因素进行识别，政治风险不仅应考虑政治因素，还应考虑对政治比较敏感的经济和社会因素，因此将政局、政策、法律、与我国外交关系、经济增长率、物价指数和社会稳定性来衡量政治风险的大小。

3.建立了基于粗糙集理论的铝矿资源海外开发战略选区政治风险灰色关联评价模型，利用粗糙集对指标进行赋权，并通过属性约简将各国差异不大的“与我国外交关系”这一指标约掉，用灰色关联分析法对13个国家的政治风险进行评价。结果表明，澳大利亚、美国、和巴西的政治风险较小，可作为铝矿资源海外开发的首选区，而印度、希腊和圭亚那等国应做好应对政治风险的措施。

[1]张伦和.铝土矿资源合理开发与利用[J].轻金属，2012（2）：3-11.

[2]张美丽.中国对外铝矿直接投资的区位选择研究[D].北京：北方工业大学，2012.

[3]邓铁军.工程风险管理[M].北京：人民交通出版社，2004.

[4]何新华，胡文发.国际环境下的项目政治风险评价模型[J].同济大学学报：自然科学版，2007（11）：1572-1577.

[5]PawlakZ.Rough Sets.InternationalJournal[J].of Computer and Information Sciences，1982（11）：341-356.

[6]张文修，仇国芳.粗糙集属性约简的一般理论[J].中国科学E辑：信息科学，2005（12）：1304-1313.

[7]李远远.基于粗糙集的指标体系构建及综合评价方法研究[D].武汉：武汉理工大学，2009.

[8]姜连馥，石永威，满杰，杨尚群.基于模糊粗糙集理论的建筑业综合评价[J].大连理工大学学报，2007（5）：729-734.

[9]张兵.基于粗糙集理论的经济圈交通枢纽灰色关联评价方法[J].重庆交通大学学报：自然科学版，2012（3）：448-454.

[10]王莹.基于粗糙集—可拓综合评价法的建筑企业社会责任评价研究[D].广州：广州大学，2012.

[11]徐建中，王莉静，赵忠伟.基于灰色关联分析的区域主导产业选择研究[J].科技进步与对策，2010（9）：51-54.

[12]穆瑞，张家泰.基于灰色关联分析的层次综合评价[J].系统工程理论与实践，2008（10）：125-130.

[13]罗印.基于灰色关联分析的中国光伏产业国际竞争力研究[D].长沙：湖南师范大学，2012.

TD-9；F272-05

A

2095-3046（2014）02-0035-07

10.13265/j.cnki.jxlgdxxb.2014.02.008

2013-12-23

教育部人文社会科学研究规划基金项目（编号：12YJA790208）

袁纬芳（1990-），女，硕士研究生，研究方向：国家经济安全、矿业技术经济，E-mail：yuerlong@126.com.

郑明贵（1978-），男，博士，副教授，研究方向：矿业技术经济，E-mail：mgz268@sina.com.