理赔量具有一阶自回归结构的离散时间风险模型的破产问题
于莉,詹晓琳,黄水弟
(1.合肥工业大学理学院,合肥230009;2.上海第二工业大学理学院,上海201209)
理赔量具有一阶自回归结构的离散时间风险模型的破产问题
于莉1,詹晓琳2,黄水弟1
(1.合肥工业大学理学院,合肥230009;2.上海第二工业大学理学院,上海201209)
在理赔量具有一阶自回归的情形下,讨论修正的经典的离散时间风险模型。利用递推形式和数学归纳法得出了破产前盈余的分布,破产前最大盈余的分布,以及破产前盈余、破产后赤字、破产前最大盈余的联合分布的递推式。
离散时间风险模型;一阶自回归;破产前盈余;破产前最大盈余;破产后赤字;分布
0 引言
早在1986年,BOWERS等[1]就对离散时间的保险模型进行了讨论。谭激扬等[2]研究了在保费和理赔量都取整数值时,离散复合Poisson风险模型的破产概率问题。杨善朝[3]研究了理赔量是随机变量的复合二项风险模型下破产概率ψ(0)的近似计算公式。孙立娟等[4]讨论了常利率的离散时间风险模型的一些破产分布。于莉等[5]讨论了在利率为独立同分布条件下的破产前最大盈余、破产赤字、破产前一时刻的盈余分布与破产持续时间分布的递推公式。于莉等[6-7]在利率具有一阶自回归结构下给出了一些诸如破产前一刻的盈余分布和破产持续时间分布的破产分布。魏瑛源等[8]利用鞅方法得到了当理赔总量满足一阶自回归模型AR(1)时最终破产概率的Lundberg上界。YANG[9]给出了带有利率的离散时间模型破产概率的非指数上界。CAI[10]讨论了相依利率下破产概率的一些结果。XU等[11]在利率为马氏链净损失为一阶自回归的离散模型下讨论了破产概率。GERBER[12]讨论了线性的破产理论。CHENG等[13]考虑了当理赔、保费和利率均为一阶自回归的基础上获得的破产概率满足的微分方程,没有讨论其他破产问题。本文在文献[8]的基础上通过递推和数学归纳法,得出了描述破产严重程度的破产前盈余分布,破产前最大盈余分布,以及破产前盈余、破产后赤字、破产前最大盈余的联合分布。
记Un为保险公司在n(n=0,1,2,···)时刻的盈余,满足

式中:u=U0表示保险公司的初始盈余;c为常数,表示单位时期(不失一般性,可假设单位时间区间(n-1,n]为第n个单位时期)内保费的收取量;Sn为前n个单位时期的理赔总量,并假设

Yi为第i单位时期的理赔总量,且满足一阶自回归模型AR(1)-1<a<1,W1,W2,···为相互独立同分布的随机变量,E[Wi]<(1-a)c。如果Y0=y0,则完全决定了Yi的AR(1)模型。当a=0时,式(1)即为经典的离散时间风险模型。

魏瑛源等[8]通过递推公式(3)对式(1)进行修正,并通过引入修正初始盈余和修正理赔总量的概念,得到修正的经典离散风险模型

破产时刻即保险公司的首次盈余小于零的时刻,则式(4)的破产时刻为

显然¯T为停时。本文将讨论在修正的经典风险模型下,描述保险公司破产严重程度的破产前盈余分布,破产前最大盈余分布,以及破产前盈余、破产后赤字与破产前最大盈余的联合分布。
1 破产前盈余的分布
保险公司的财务状况以及偿付能力是保险人和投保人都十分关心的问题,为了弄清楚保险公司出现入不敷出的实际状况,研究破产前瞬时保险公司的盈余情况是非常必要的。1988年Dufresne和Gerber首次引入描述破产前盈余分布状况的函数,有关问题立即成为破产理论中的重要研究论题。本节在理赔量具有一阶自回归的结构下,对这一问题进行讨论。
引入函数F(¯u,x),定义为

F(¯u,x)描述了准备金为¯u时破产前瞬时盈余大于x的概率,由式(6),有

式中,gn(¯u,x)是破产时刻为n的瞬时盈余大于x的概率。则

同理

注意,式(9)最后一个等号后的第二项为0,这是由于在该项中w∈[¯u+c-x,¯u+c)即x>¯u+c-w>0,由式(8)可知此时g1(¯u+c-w,x)=0。由此,式(9)成为

类似地,有

由数学归纳得到,对于n≥2,有


式中,g1(¯u,x)由式(8)给出。
2 破产前最大盈余的分布
了解保险公司在破产前最大盈余的分布,适时地将保险进行投资,对于增加保险公司的收入以及增强保险公司的偿付能力都是十分必要的。本节在理赔量具有一阶自回归的结构下,对这一问题进行讨论。
定义初始资本为¯u时破产前最大盈余分布函数为

当x<¯u时,显然有H(¯u,x)=0,故只需讨论x≥¯u的情形。由式(14)可得

式中,hn(¯u,x)是破产时刻为n的破产前最大盈余分布,并约定¯S0≡0。
由定义得

类似地,有


由数学归纳法,对于n≥2,有


式(20)即为保险公司在破产前最大盈余所满足的积分方程。
3 破产前盈余、破产后赤字与破产前最大盈余的联合分布
对x>0,y>0,z>0,定义

为破产前盈余、破产后赤字与破产前最大盈余的联合分布,这里停时¯T为破产时间。
显然当z<¯u时,D(¯u,x,y,z)=0。以下只对z≥¯u的情况作讨论。
(1)首先当x≤z时,由式(21),有
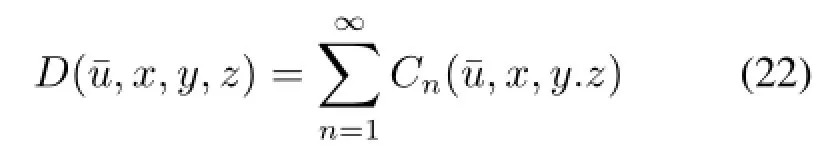
在¯T=n时,破产前盈余、破产后赤字与破产前最大盈余的联合分布为

采用递推算法,当n=1,2时

注意,式(25)最后一个等号后的第二项为0,这是由于在该项w∈[¯u+c-z,¯u+c-x)即x<¯u+c-w>0,由式(24)可知,此时C1(¯u+c-w,x,y,z)=0。故式(25)成为

类似地,有

由数学归纳法得,对n≥2,有

由式(22)、式(24)、式(28)知,

(2)对于x>z的情形,由于

所以,有

这时D(¯u,x,y,z)实际上描述了破产后赤字与破产前最大盈余的联合分布,记为D(¯u,y,z)。与前面的推理完全类似,由数学归纳法可以得到

4 结论
本文给出了在经典的风险模型下当理赔量为一阶自回归结构时的破产前盈余分布,破产前最大盈余分布,以及破产前盈余、破产后赤字、破产前最大盈余的联合分布满足的积分公式。在此想法的基础上,今后还可以在一般的离散时间风险模型和广义的离散时间风险模型下给出一些类似的问题进行讨论。在本文所满足的关系式中,如果能够收集到某一时刻某一保险公司的初始盈余、满足一阶自回归结构的理赔量的实际值,则可以通过实际数值的拟合,来对所得到的结论进行验证,这将使结论更具有实际意义。
[1]BOWERS N L,GERBER H U,HICKMAN J C,et al.Actuarial mathematics[M].Itasca Illinois:Society of Actuaries,1986.
[2]谭激扬,杨善朝.离散时间的双Poisson模型的破产问题[J].应用概率统计,2005,2(3):235-243.
[3]杨善朝.复合二项风险模型破产概率ψ(0)的近似计算[J].广西师范大学学报.2003,21(4):48-52.
[4]孙立娟,顾岚,刘立新.离散时间模型下最大赤字问题[J].经济数学,2001,18(4):1-9.
[5]于莉,詹晓琳.带有变利率的离散时间风险模型的破产分布[J].合肥工业大学学报,2009,32(2):273-277.
[6]于莉,杜雪樵.相关利率下离散时间风险模型的破产分布[J].科学技术与工程,2007,19(7):4805-4807.
[7]孔繁超,于莉.具有相依利息率的离散时间保险风险模型的破产问题[J].高校应用学报,2005,20(3):320-326. [8]魏瑛源,唐应辉.离散时间风险模型的推广研究[J].电子科技大学学报,2006,35(3):426-428.
[9]YANG H L.Non-exponential bounds for ruin probability with interest effect included[J].Scandinavian Actuarial, 1999(1):66-79.
[10]CAI J.Ruin probability with dependent rates of interest[J]. Journal of Applied Probability,2002,39(2):233-454.
[11]XU L,WANG R M.Upper bounds for ruin probability in an autoregressive risk model with a Markov chains interest rate[J].Journal of Industrial and Management Optimization,2006,2(2):165-175.
[12]GERBER H U.Ruin theory in the linear model[J].Insurance:Mathematics and Economics,1982,1(3):213-217.
[13]CHENG J H,WANG D H.Ruin problems for an autoregressive risk model with dependent rates of interests[J]. Applied Mathematicas and Computation,2011,218(7): 3822-3833.
Ruin Problems for the Discrete Time Insurance Risk Model with AR(1)Claim Sizes
YU Li1,ZHAN Xiao-lin2,HUANG Shui-di1
(1.School of Science,Hefei University of Technology,Hefei 230009,P.R.China;2.School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)
The modifed classical discrete time insurance risk model with AR(1)claim sizes was discussed.Using recursive method and mathematical induction,recursive expressions about the distribution of surplus before ruin and maximum surplus before ruin,as well as the recursive expressions of the joint distribution of surplus before ruin,defcit after ruin,and the maximum surplus before ruin were derived.
discrete time insurance risk model;AR(1);surplus before ruin;maximum surplus before ruin;defcit after ruin;distribution
O211
:A
会展经济研究组织召开专题座谈活动
1001-4543(2014)01-0061-06
2013-08-20;
2014-02-27
詹晓琳(1978–),女,安徽蚌埠人,副教授,硕士研究生,主要研究方向为概率统计,电子邮箱xlzhan@sf.sspu.cn。
简讯
2014年2月26日上午,会展经济研究所在图文信息中心赏宝厅举行专题座谈活动。本次活动是应曙光研究院2014年度“走群众路线”系列活动要求,主要围绕会展青年教师实际需求展开,通过面对面的交流与畅谈,深入细致了解会展青年教师们的真实想法以及对会展研究所和曙光研究院的期望,增进了解同时促使会展经济研究和曙光研究院本年度工作计划更贴近实际、解决教师所需。活动由会展经济研究所所长辜应康老师主持,曙光研究院郝皓院长、张淑平副院长、于伟副院长、徐爱萍老师以及会展经济研究所全体青年教师出席了活动。郝皓老师首先就曙光研究院定位、宗旨、发展历程以及学校对研究院的新要求进行了阐释,张淑平老师和于伟老师作了补充。然后会展经济研究所每位青年教师就各自学习、工作和研究经历进行了介绍和交流,同时就学历晋升、职称评定、专业培训、个人发展、研究方法等方面进行了热烈讨论并与曙光研究院领导和老师进行了积极互动,提出了很多很好的意见和建议,对进一步优化和落实会展经济研究所和曙光研究院本年度工作意义重大。

