一类具有范数有界不确定性的非线性时滞系统的控制
刘碧玉,冯良文,胡顺新,颜爱民,王晓丽,刘建刚
(1.中南大学数学与统计学院,湖南长沙 410083;2.中南大学商学院,湖南长沙 410083;3.中南大学信息科学与工程学院,湖南长沙 410083)
0 引 言
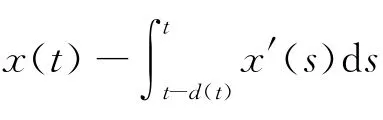

1 系统描述
考虑如下满足Liptchitz条件且具有范数有界不确定性的非线性时滞系统

式中:x(t)∈Rn,u(t)∈Rm,z(t)∈Rm1,w(t)∈Rm2分别是系统的状态向量,控制输入向量,被控输出向量,干扰输入向量,A,A d,B,C,D,D1为适当维数的已知实常矩阵,ΔA,ΔA d,ΔB,ΔC,ΔD,ΔD1是具有适当维数的实函数矩阵,表示系统的不确定性,且这些参数矩阵范数有界并满足
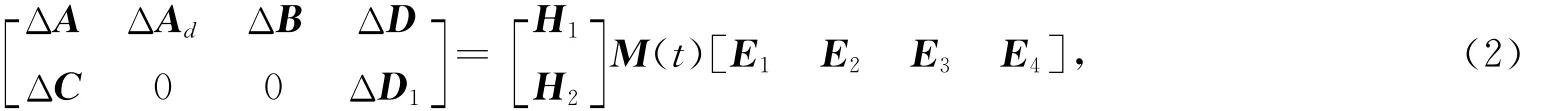
式中:H1,H2,E1,E2,E3,E4是已知的具有适当维数的常数矩阵.M(t)∈Ri×j是一个具有Lebesgue可测元的未知矩阵函数,且满足

式中:I表示适当维数的单位矩阵;d(t)为系统状态滞后,且存在正实数τ,v,使得对所有的时间t满足

引理1 函数f(x)是满足条件的,即对任意的x∈Rn和∈Rn,都存在一个常数矩阵L,使得式(6)成立
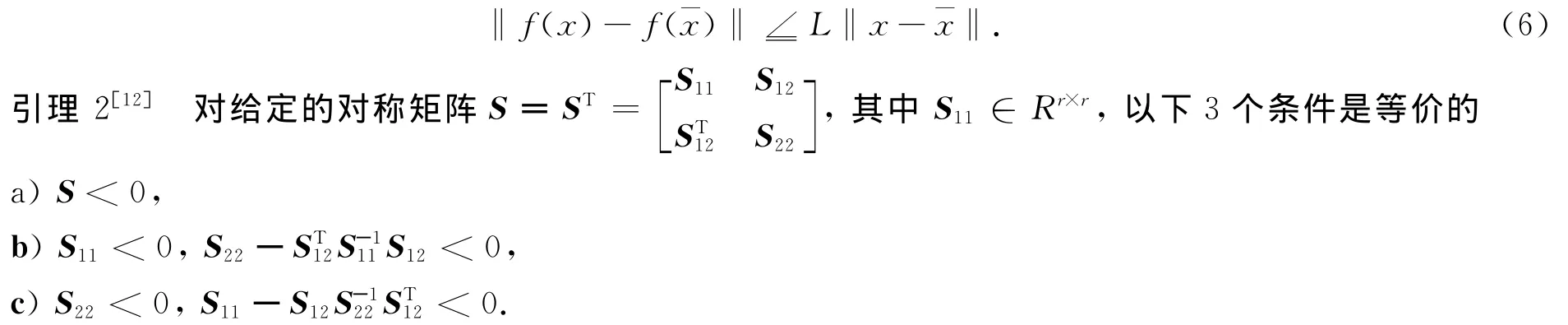
引理3[13]设X,Y,Z是给定的k×k阶实对称矩阵,满足X0,且对xTZx0的所有非零向量x∈Rk,有

则存在常数λ0,使得式(7)成立

假设1 设计一个线性状态反馈控制律

当w(t)=0时,得到系统(1)的闭环系统


定义1 (H∞-γ控制)对于闭环系统(9),寻找所有真的实有理控制器K,使闭环控制系统内部稳定,且闭环传递函数矩阵T zw(s)的H∞范数小于一个给定的常数γ<0,即

注:G(s)∈H∞为系数的传递函数矩阵,z=G(s)w为系统的输出.
2 主要结果
定理2.1 针对非线性不确定时滞系统(1),给定正标量τ>0和v<1,如果存在n×n阶正定对称矩阵P=PT>0,R1=0,R2=>0,以及适当维数矩阵N i,T i(i=1,2,3,4),使得式(10)矩阵不等式成立

则称系统式(9)在满足条件式(4)和式(5)下是鲁棒二次稳定的.其中

证明:构造如下Lyapunov泛函




对于任意的w(t)∈L2[0,+∞)且w(t)≠0时,有如下定理:
定理2.2 系统式(1)是具有H∞性能γ当且仅当存在适当维数矩阵N i,T i,S i(i=1,2,3,4,5),Q及正定对称矩阵P=PT>0,R1=0,R2=>0和标量α>0,β>0使得式(18)成立

而且如果式(18)满足,则状态反馈控制器

为一鲁棒H∞-γ镇定控制器.
证明 对任意满足式(3)的不确定性M(t),构造同定理2.1的Lyapunov泛涵,并且令

取Ψ=zT(t)z(t)-γ2wT(t)w(t)+V′(x(t)).
将式(12)~式(14)改动如下

由schur补可知Θ等价于下面矩阵不等式

显然,式(23)等价于任意具有适当维数的非零向量ζ,式(24)满足

其中标称项



时式(24)左边取最大值,此时需满足


注:通过求解以下的凸优化问题,可以求得闭环系统最优的H∞性能指标γ*以及相应的鲁棒H∞-γ控制器.

3 数值仿真

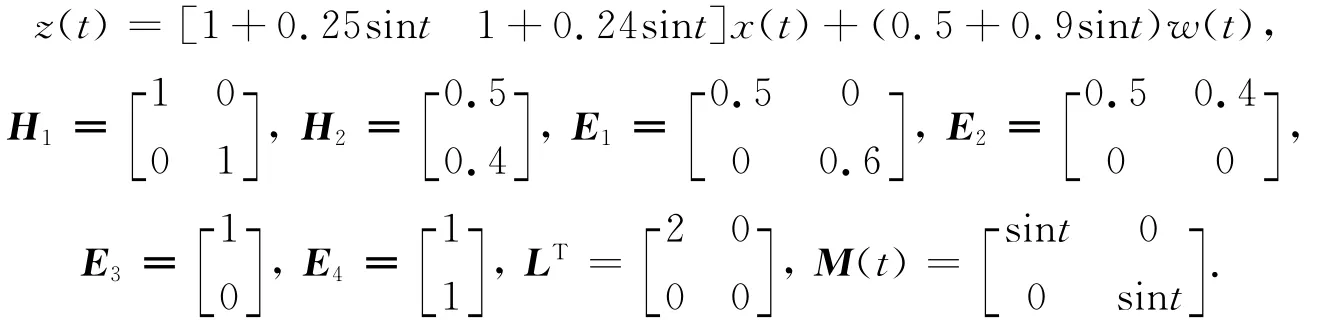
利用Matlab软件求解凸优化问题(33)即可得到范数有界不确定性的非线性时滞系统的最优H∞-γ控制器u*=-0.498 2x1+0.001 8x2,相应的干扰抑制度为γ*=1.340 636e-005.
4 结 论
本文结合自由权矩阵,牛顿-莱布尼兹公式,给出了范数有界不确定性系统的鲁棒控制二次稳定的充分条件,但是本文采用的是线性状态反馈,而实际中的状态反馈多为非线性的,此外本文中时滞的范围有些宽,实际系统中时滞一般是大于零的,即时滞的范围要小些,对于这些问题还需进一步研究.
[1] Moon Y S,Park P,Kwon WH,et al.Delay-dependent robust stabilization of uncertain state-delayed sstems[J]Int.J.Control,2001,74(14):1447-1455.
[2] Han Qinglong,Gu Keqin.On robust stability of time-delay systems with norm-bounded uncertainty[J].Automat.Contr.,2001,46(9):1426-1431.
[3] Saleh S.Delshad,Thomas Gustafsson,Andreas Johansson.Observer Design for uncertain Discrete-Time Nonlinear Delay Systems:LMI Optimization Approach[C].20th Mediterranean Conference on Control &Automation,Barcelona,Spain,2012:592-597.
[4] Fridman E,Shaked U.A descriptor system approach to control of time-delayed systems[J].Auto.Contr.,2002,47(2):253-279.
[5] Fridman E.New Lyapunov-Krasovskii functionals fir stability of linear retard and neutral type systems[J].Syst.Contr.Lett.,2001,43(4):309-319.
[6] Li X,de Souza C E.Criteria for robust stability of uncertain linear systems with time-varying state delays[C].Proc.of 13th World Congress of IFAC,San Francisco,UAS,1996b,137-142,.
[7] Yu L,Chu J.An LMI approach to guaranteed cost control of linear uncertain time-delay systems[J].Automatica,1999,35(6):1155-1160.
[8] Choi H H,Chung MJ.Memoryless stabilization of uncertain dynamic systems with time-varying delayed states and controls[J].Automatica,1995,31(9):1349-1351.
[9] Kim J H,Jeung E T,Park H B.Robust control for parameter uncertain delay systems in state and control input[J].Automatic,1996,32(9):1337-1339.
[10] Su H Y,Chu J,Wang J C.A memoryless robust stability control for a class of uncertain linear time-delay systems[J].Int,J.System Science,1998,29(2):191-197.
[11] Yu L,Chen G D,Memoryless stabilization of uncertain linear systems with time-varying state and control delays[J].Advan.Mod.Ana,Series C,49(1):27-34
[12] 吴敏,桂卫华,何勇.现代鲁棒控制[M].长沙:中南大学出版社,2006.
[13] 苏宏业,褚健,鲁仁全.不确定时滞系统的鲁棒控制理论[M].北京:科学出版社,2007.

