基于LQR方法的扭转振动装置控制器设计

王佳伟， 杨亚非， 钱玉恒

(哈尔滨工业大学 飞行器控制实验教学中心，黑龙江 哈尔滨 150001)

0 引 言

扭转振动简称扭振，是一种常见的机械振动物理现象，当弹性体绕其纵轴发生扭转变形时，就会产生扭转振动。扭振大多见于电力系统的汽轮发电机组[1-4]、汽车发动机的曲轴系[5-8]、轧钢机的传动机组[9-11]，以及石化行业的烟机等应用场合。

Model205a型扭转振动装置是由世界知名的教学设备生产企业美国ECP公司生产制造的，已经在世界上500所大学中推广应用，其功能和性能都明显优于国内单位使用或设计的扭振实验台[12-14]。该装置可以模拟单自由度、双自由度和三自由度系统的扭转振动特性，分析激励频率对系统固有频率的影响，即分析扭振装置的频率响应。该装置的另外主要功能在于，它是一个数字控制的闭环控制系统，机械部分是一个真实的控制对象，控制器则通过计算机来进行设计，整体相当于一个半实物的仿真平台，可以对其进行各种控制器的设计和仿真验证。本文将其机械部分配置成四阶的双自由度的被控对象，通过受力分析推导其等价的数学模型，然后将为其设计一种LQR控制器，最后将经过实验仿真来验证控制器的作用效果。

1 装置简介

实验装置如图1所示。

图1 扭转振动装置组成

(1) 扭转振动装置的机械部。如图2所示，扭转振动装置由扭转机械部分、执行器和传感器构成。扭转机械部分是由底座、框架、扭转轴、圆盘、惯量砝码等组件构成；执行器采用了无刷直流伺服电机；传感器选用了高分辨率的编码器。机械部分的弹性轴垂直悬挂在抗摩擦球形轴承上，用来连接3个圆盘。伺服电机通过刚性皮带(仅存在微小拉伸形变)来驱动底层圆盘和弹性轴，滑轮系统的减速比为3∶1，每个圆盘都配有一个编码器来测量圆盘的位置。

图2 扭转振动装置的机械部分

(2) M56000系列的DSP控制器板卡和输入输出电箱组成的控制系统。如图3所示，DSP控制器能够以高采样率来执行控制律，解释轨迹命令，并支持数据采集、轨迹生成、系统状态及安全检测等功能。板卡中还包括可以实现编码器脉冲解码逻辑门阵列和2个进行实时模拟信号测量的辅助数模转换器(DAC)。控制器的板卡与实际工业控制中使用的板卡相同。电箱主要功能是为机械部提供驱动电压，同时接收编码器的反馈信号，返回到控制器的板卡上，进而为执行程序提供测试数据。

图3 控制系统部分

(3) 系统执行软件。系统执行软件即应用软件和用户界面，它支持控制器指定、轨迹定义、数据采集、绘图系统执行指令等功能。执行软件支持使用直观的“类C”语言来编写控制器算法程序，并且运行控制器。内置的自动编译器为执行程序代码的提供有效传送和运行。此外，该执行软件还提供了与其他应用软件的接口，可以与Matlab软件进行连接调试。执行软件的运行窗口如图4所示。

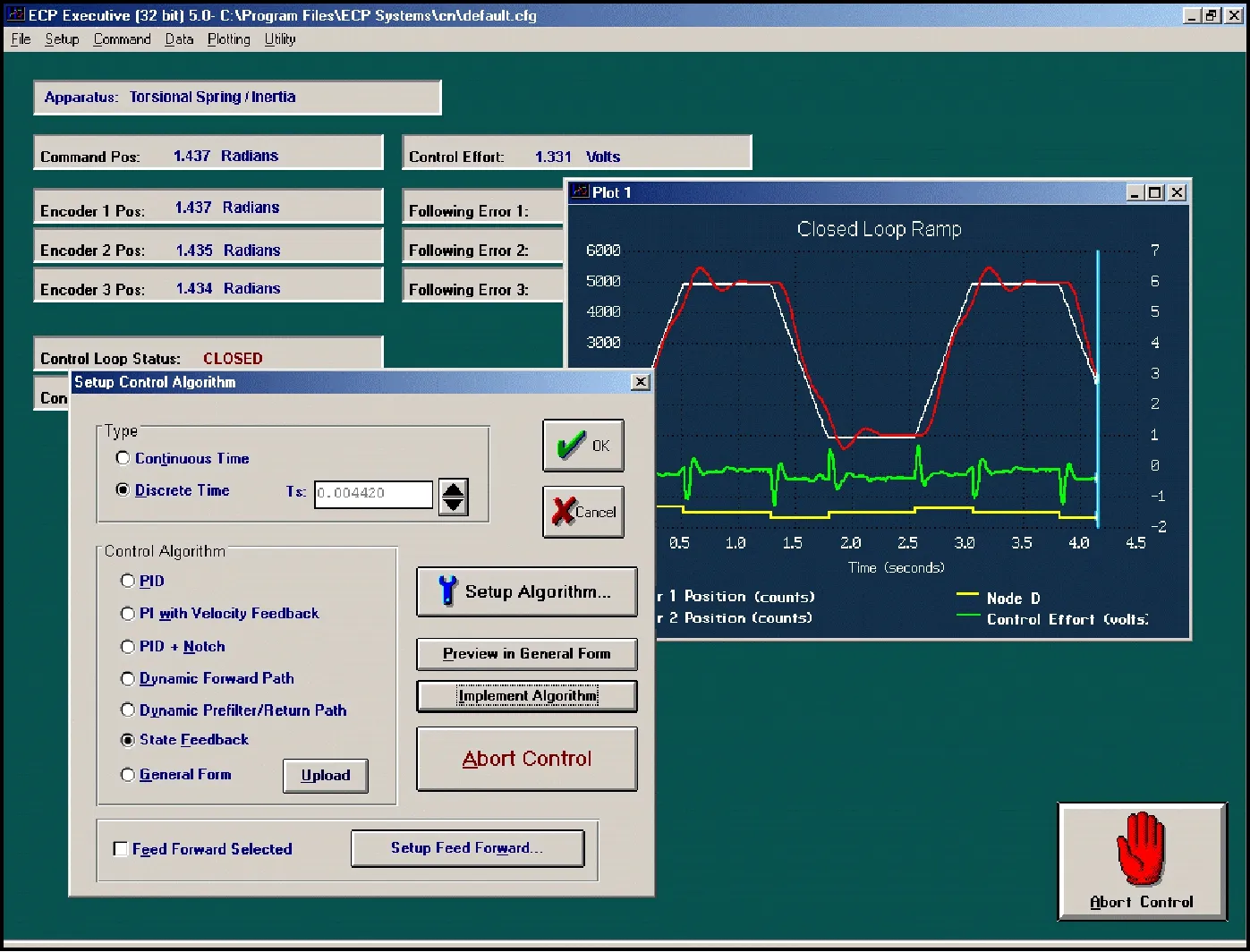
图4 执行软件的运行窗口

用户可以编写执行程序中的控制算法，然后将其加载到基于DSP的实时控制板卡上，DSP在每个指定的采样周期执行此算法，读取参考输入和反馈传感器(光电编码器)的值，经过计算将数字控制效果信号输出到DAC，DAC将数字流转换为一个模拟电压，然后通过一个伺服放大器转换为电流，再通过电机变为转矩，电机根据设备动力学特性将电机的输入转变为所期望的输出。设备完成指定的动作后，传感器的测试数据通过电箱回传到执行软件中，用于绘图和存储。

2 双自由度对象的模型推导

实验装置可配置为双自由度的系统，如图5所示(忽略摩擦)。输入为转矩T(t)，输出为第1个圆盘的角度θ1(t)和第2个圆盘的角度θ2(t)，2个圆盘的惯量分别为J1和J2，弹簧的弹性系数为k1。

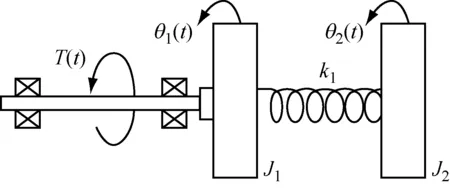
对2个圆盘进行受力分析及根据牛顿第二定律得到运动方程为：

(1)

对上式两边取拉普拉斯变换，并假设初始条件为零，得到传递函数为：

(2)

用状态空间法表示为

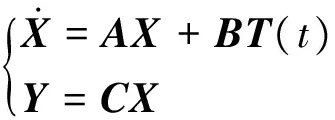
(3)

其中：

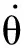
当Y=Xi(i=1,2,3,4),且其余量为零时，ci=1(i=1,2,3,4)。

通过数学模型可知，该模型为四阶二型的系统，结构可以看成是刚体加一阶振荡模态组成，可以模拟单输入单输出、单输入多输出的系统。对于该模型的进行控制算法的研究，具有重要的应用意义。

3 LQR控制器的设计及仿真验证

LQR(Linear Quadratic Regulator)最优设计指的是设计出的状态反馈控制器K要使二次型目标函数J达到最小值，其中K由权矩阵Q与R唯一决定，因此对于参数Q和R的选择十分重要。通过LQR方法，可以得到状态线性反馈的最优控制规律，易于构成闭环最优控制。对于线性系统的控制器设计问题，如果其性能指标是状态变量和控制变量的二次型函数的积分，则这种动态系统的最优化问题称为线性系统二次型性能指标的最优控制问题，简称为线性二次型最优控制问题或线性二次问题。其最优解可以写成统一的解析表达式以实现求解过程的规范化，并可简单地采用状态线性反馈控制律构成闭环最优控制系统，同时能够兼顾多项性能指标，因此受到控制界学者的广泛关注，并且在一些实验装置中获得了应用[15-16]。

针对双自由度的扭转控制装置，设计LQR控制器来对其进行控制，并通过在装置上的实验来验证控制律的有效性。

3.1 LQR控制器设计

利用式(2)双自由度对象传递函数可得到LQR控制的闭环系统频域结构框图，见图6(a)。系统的输出为第2个圆盘的角度θ2(t)，反馈信号选择为θ1(t)和θ2(t)，对应反馈通道的为2个一阶微分环节，传递函数为k1+k2s和k3+k4s，闭环回路传递函数为：

(4)

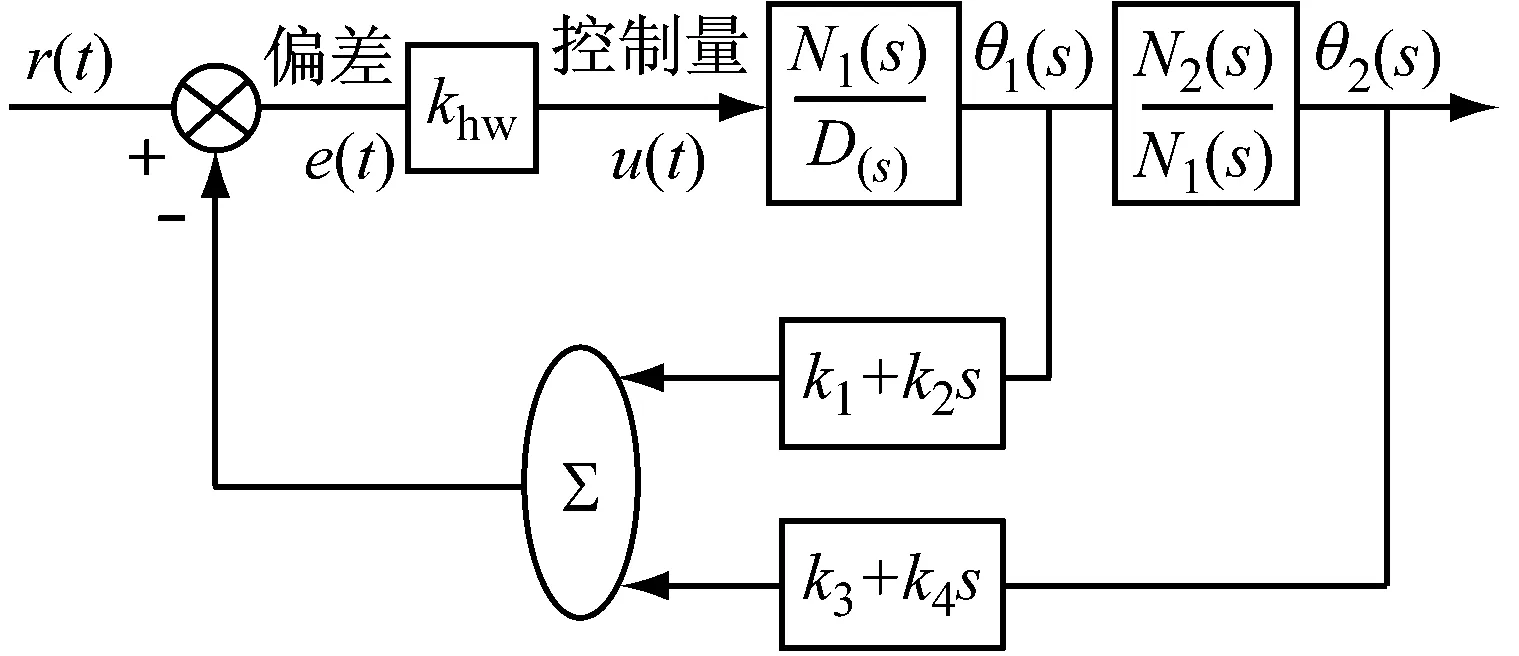
图6(b)给出了双自由度对象的全状态反馈控制的闭环时域结构图，对象使用式(3)给出的状态空间模型描述，khw表示装置的硬件增益，状态选择为圆盘1和2的角度和速度，输出选择为θ2(t)，系统为单入单出系统，则输出矩阵选择：

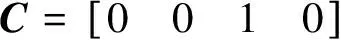
(5)

利用全状态反馈控制设计一个LQR控制器，设计反馈率：

u=-Kx

(6)

其中：K=[K1K2K3K4]，线性二次型性能指标函数选择为

(7)

设计目标是对于给定已知的Q和R，找到能最大限度减小指标函数的控制器K，

K=R-1BTP

(8)

其中，P满足如下代数黎卡提方程：

ATP+PA-PBR-1BTP+Q=0

(9)

通过求解黎卡提方程就可以得到P和K，进而实现LQR控制。至此，针对双自由度对象完成了LQR控制器的设计。

3.2 LQR控制器参数计算

在图6(b)中，对象状态空间模型的参数矩阵A，B由式(3)给出，其中,J1,J2表示圆盘的转动惯量;k1表示弹簧系数，均为已知参数，则:

(10)

(11)

根据式(5)，参数Q选取为

(12)

这种参数选择可以使出现在输出θ2(t)误差减小，并且可以降低控制量的损耗。然后设定6种情况下的控制量权值R：R=100，10，1.0，0.1，0.01和0.001。

为求解黎卡提方程，使用Matlab软件中的函数

[K,P,E]=LQR(A,B,Q,R)

(13)

将参数A,B,Q,R代入上式，可得出每种情况下的K值以及闭环极点E，即[A-BK]的特征值。绘制出6种不同情况对应的闭环极点的图形。

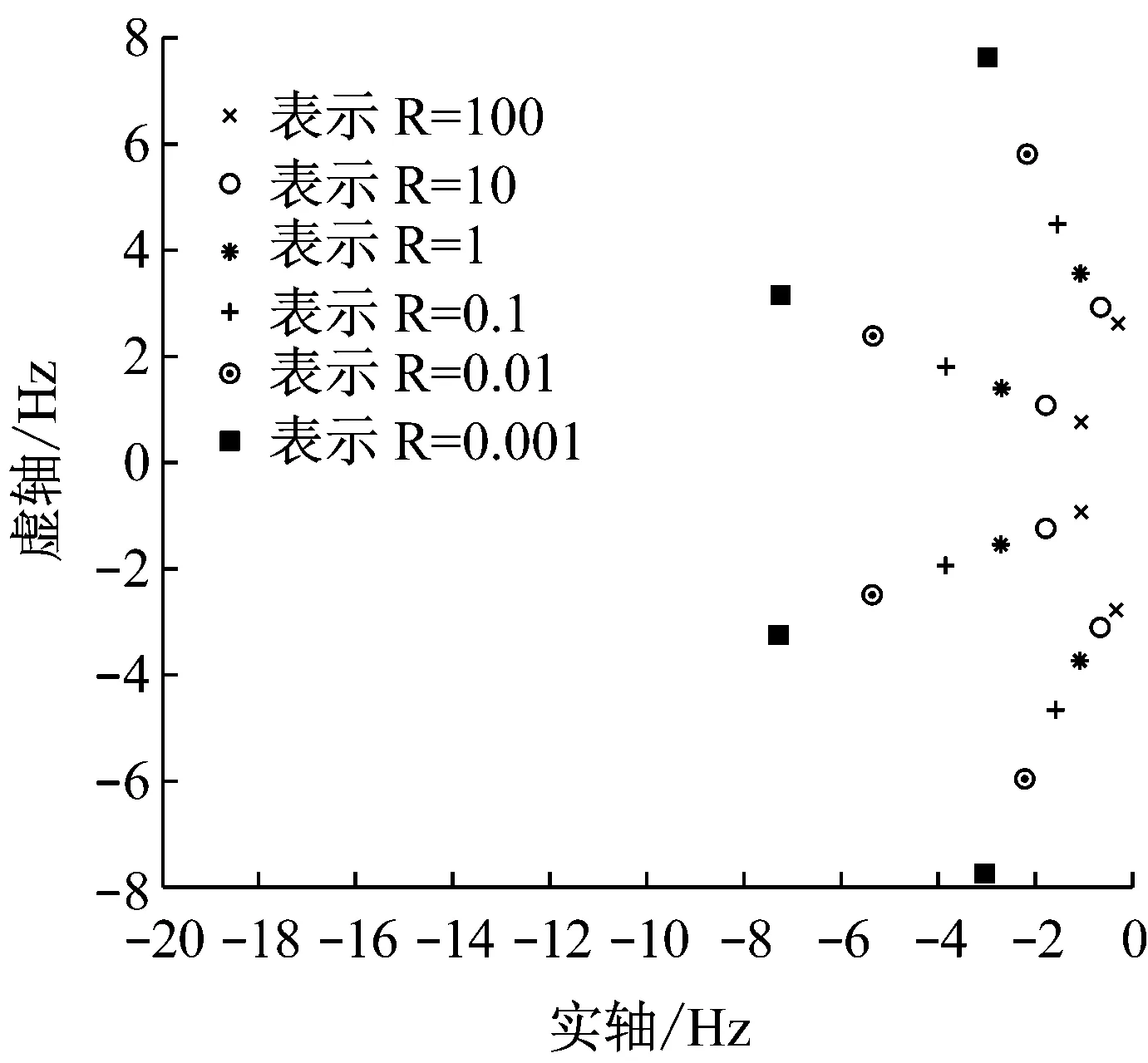
从所得数据中选择一个最低极点频率位于2.75～3.25 Hz间的闭环极点。使用该极点对应的K值，要求分量中K1和K3的值不要大于1，K2和K4的值不要大于0.12。得到的符合上述要求的合适的控制器是R=10时的情况，计算的控制器K为

K=[0.717 0 0.029 4 0.283 0 0.084 7]

3.3 仿真验证

通过系统辨识的实验，可以确定khw的值。将计算得到的控制器K参数输入到软件中，得到一个闭环的控制系统。

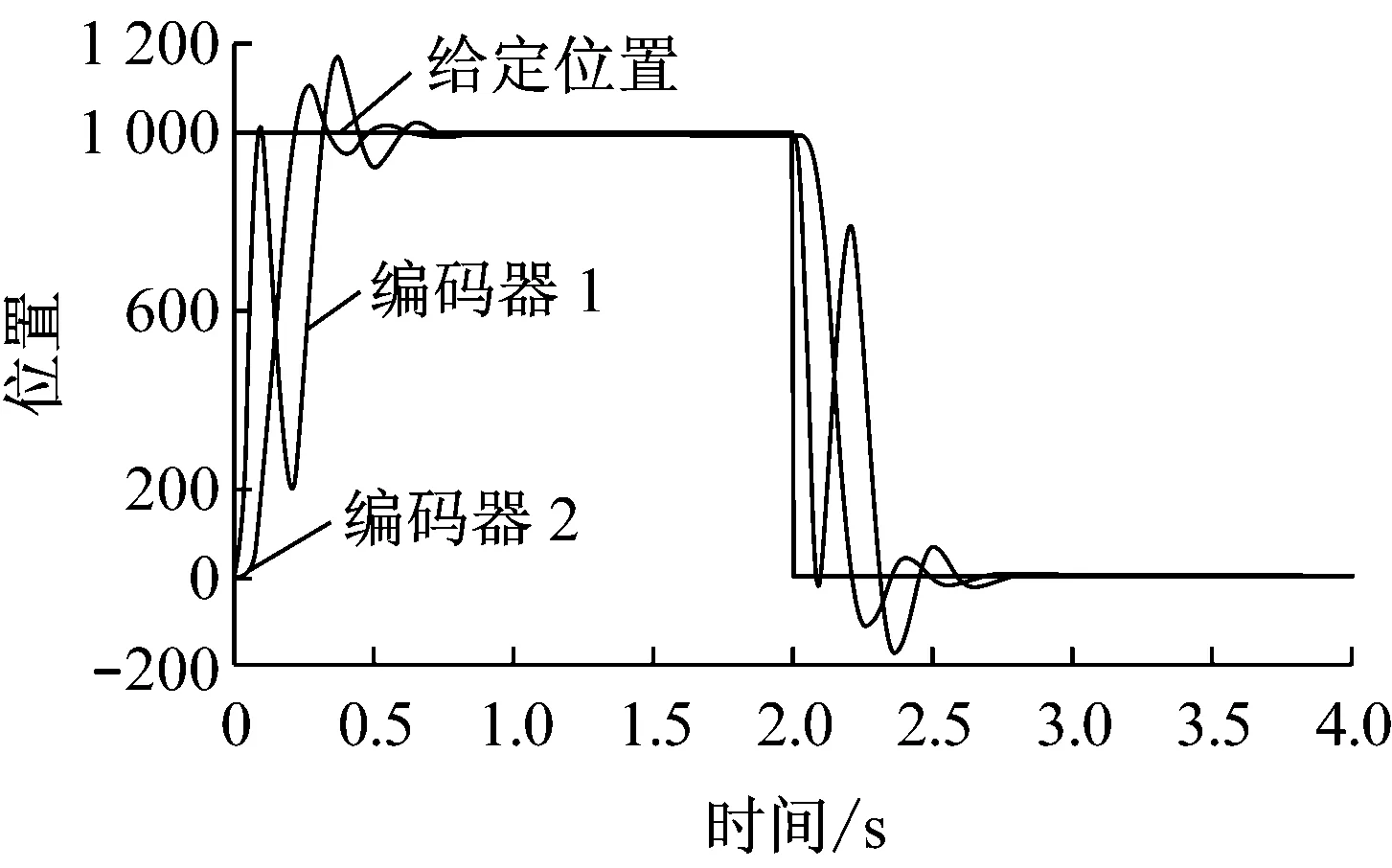
仿真步骤：设置输入幅值为1 000，持续时间为2 s，重复次数为1的阶跃信号；选择控制器类型为State Feedback，分别输入控制器K1、K2、K3、K4的参数，并加载到控制器中，设置数据采集，绘制编码器1、2和给定位置的数据，得到对象的阶跃响应曲线如图8所示。由响应图形可知，系统响应速度较快，超调量也比较小，证明所设计的LQR控制器具有良好的控制性能。

4 结 语

本文首先对美国ECP公司的扭转振动装置的系统组成、性能和所能实现的功能进行概要介绍。然后对于该装置的一种等效的双自由度系统模型，设计了LQR控制器，并验证了控制器的效果。本实验加深了对现代控制理论中的控制器设计方法的理解，为学生进一步学习更复杂的控制方法打下基础。

[1] 谢诞梅，刘占辉，杨长柱，等.汽轮发电机组轴系扭转振动对机械参数的敏感性分析 [J]. 动力工程，2005，25(4): 462-465.

XIE Dan-mei，LIU Zhan-hui，YANG Chang-zhu，etal. Sensitivity Analysis of the Torsional Vibration Behavior of a Turboset’s Rotor System to Changes of Its Mechanical Parameters [J]. Journal of Power Engineering，2005，25(4): 462-465.

[2] 刘 宝，杨雪静，李 岩. 汽轮发电机组轴系扭振动态响应计算分析[J]. 机电工程技术，2011，40(12): 70-74.

LIU Bao，YANG Xue-jing，LI Yan. Calculation and Analysis of Dynamic Response of Steam Turboset Shafting [J]. Mechanical & Electrical Engineering Technology，2011，40(12): 70-74.

[3] 胡俊宏，高 峰，孙振鲁. 汽轮发电机组轴系扭振模拟试验台研制[J]. 机械设计与制造，2012(10): 96-98.

HU Jun-hong，GAO Feng，SUN Zhen-lu. The Development of an Experiment Rig for Studying Torsional Vibration[J]. Machinery Design & Manufacture，2012(10): 96-98.

[4] 苏永丽，康积涛，吴小刚. 汽轮发电机轴系扭振模态分析 [J]. 电气开关，2013(5): 66-69.

SU Yong-li，KANG Ji-tao，WU Xiao-gang. Shaft Torsional Vibration Mode Prediction of Turbine Generator [J]. Electric Switchgear，2013(5): 66-69.

[5] 于学华. 发动机曲轴系统扭转振动分析 [J]. 汽车技术，2008(3): 15-18.

YU Xue-hua. Analysis of Torsional Vibration in Crank shaft System [J]. Automobile Technology，2008(3): 15-18.

[6] 张 芳，王必璠，李显戴. 车用发动机扭转振动的分析与控制[J]. 汽车科技，2011(2): 47-51.

ZHANG Fang，WANG Bi-fan，LI Xian-dai. Torsional Vibration Analysis and Control for Engine on Vehicle [J]. Auto Mobile Science & Technology，2011(2): 47-51.

[7] 车定新. 发动机曲轴扭振计算与实验分析研究[D]. 广州： 华南理工大学， 2012.

[8] 陈 翔，崔志琴. 发动机曲轴轴系扭振技术研究的方法分析[J]. 机械工程与自动化，2012(6): 216-217.

CHEN Xiang，CUI Zhi-qin. Current Situation and Prospect of Engine Crankshaft Torsional Vibration technology Research [J]. Mechanical Engineering & Automation，2012(6): 216-217.

[9] 周金宇，陈占福. 粗轧机主传动扭振分析[J]. 钢铁，2007，42(5): 51-54.

ZHOU Jin-yu，CHEN Zhan-fu. Torsional Vibration Analysis of Rougher Main Driving System of Rolling Mills [J]. Iron & Steel，2007，42(5): 51-54.

[10] 王 勤. 轧机主传动系统的扭振分析与建模[J]. 冶金设备，2009(4): 6-9.

WANG Qin. Analysis and Modeling about Torsion Vibration for Main Drive System of Mill [J]. Metallurgical Equipment，2009(4): 6-9.

[11] 刘浩然，张业宽，李晓梅. 轧机非线性传动系统冲击扭振的研究与抑制[J]. 振动与冲击，2010，29(7): 179-183.

LIU Hao-ran，ZHANG Ye-kuan，LI Xiao-mei，etal. Investigation and Suppression of Impact Torsional Vibration of a Rolling Mill’s Nonlinear Drive System [J]. Journal of Vibration and Shock，2010，29(7): 179-183.

[12] 郁 飞，王天荣，许 勃. 激光扭振仪调整、应用与误差分析[J]. 实验室研究与探索，2001，20(4): 57-58.

YU Fei，WANG Tian-rong，XU Bo. Adjustment, Application and Error Analyzing of the Torsional Vibration Meter [J]. Research and Exploration in Laboratory，2001，20(4): 57-58.

[13] 王炳辉，冯志敏，胡志钢. 智能多通道的轴系扭振试验台[J]. 实验室研究与探索，2004，23(2): 41-43.

WANG Bing-hui，FENG Zhi-min，HU Zhi-gang. An Intelligent Multichannel Shafting Torsional Vibration Tester[J]. Research and Exploration in Laboratory，2004，23(2): 41-43.

[14] 刘振峰，常 非. 柔性轴扭振系统实验台及其实验[J]. 实验室研究与探索，2009，28(8): 45-47.

LIU Zhen-feng，CHANG Fei. Research on Flexible Torsional System Design Methods [J]. Research and Exploration in Laboratory，2009，28(8): 45-47.

[15] 李劲松，颜国正，冯剑舟,等. 基于线性二次型最优控制策略的倒立摆实验系统搭建[J]. 实验室研究与探索，2010，29(3): 38-40.

LI Jin-song，YAN Guo-zheng，FENG Jian-zhou ，etal. Construction of the Inverted-Pendulum Experimental System Based on LQR [J]. Research and Exploration in Laboratory，2010，29(3): 38-40.

[16] 袁 浩，刘继光，李保林. LQR 控制策略在旋转机架模型中的应用[J]. 实验室研究与探索，2010，29(3):54-56.

YUAN Hao， LIU Ji-guang， LI Bao-lin. Application of LQR Control Strategy in a Rotary Gantry System [J]. Research and Exploration in Laboratory，2010，29(3): 54-56.