基于GWR的中国地级城市SO2年均质量浓度模拟

卢亚灵，蒋洪强*，黄季夏，徐丽芬

1. 环境保护部环境规划院 国家环境保护环境规划与政策模拟重点实验室，北京 100012；2. 中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室，北京 100101；3. 北京大学城市与环境学院 地表过程分析与模拟教育部重点实验室，北京 100871

基于GWR的中国地级城市SO2年均质量浓度模拟

卢亚灵1，蒋洪强1*，黄季夏2，徐丽芬3

1. 环境保护部环境规划院 国家环境保护环境规划与政策模拟重点实验室，北京 100012；2. 中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室，北京 100101；3. 北京大学城市与环境学院 地表过程分析与模拟教育部重点实验室，北京 100871

中国城市空气污染问题已经引起广泛关注。目前相关研究很多，但是以空间位置为拟合参数，对空气质量进行回归模拟的研究较少。以2010年中国地级以上城市SO2年均质量浓度为因变量，分别应用普通线性回归和地理加权回归（GWR）模型模拟SO2年均质量浓度，其中地理加权回归方法考虑了空间位置的影响并以此作为回归参数。回归的自变量指标体系包括气象要素（多年平均温度、光照、降水）、植被覆盖（NDVI）、地形要素（坡度、坡向、起伏度）、人为因素（GDP、能源消费）几个方面。由于各指标之间存在较强的相关性，用主成分分析方法计算得到温度、日照、降水、NDVI表征的气象植被综合指标，高程、坡度、起伏度表征的地形综合指标，和GDP、能源消费表征的人为因素综合指标。用3个综合指标值作为自变量进行回归模拟。普通回归结果较差，其r2为0.11，矫正的r2为0.10；GWR模型模拟结果相对较好，其拟合优度显著提高，r2为0.66，矫正的r2为0.47。因此，地理加权回归适合进行此类拟合，普通线性回归不适合。通过对比地理加权回归模拟的各个城市的拟合优度，发现年均质量浓度数值较高的地区拟合效果较差，这些地区主要集中在中国华北和南部部分地区。与基于机理的模型相比，GWR模型和其各具优缺点，GWR的优势主要表现在数据及其格式化要求低，计算机软硬件条件要求低，运算速度快等。

地级以上城市；地理加权回归（GWR）；SO2；年均质量浓度

随着城镇化、工业化水平的快速提高，大气污染已经成为中国突出的城市环境问题(孟晓艳等, 2012)，直接影响居民身体健康、经济生产和社会活动，甚至影响植物生长和文物古迹的保护(KAN和CHEN, 2004；JEONG等, 2005)。因此严重的大气污染可以造成严重的健康损害和经济损失(ZHANG等, 2007; ZHANG等, 2006)。目前中国大气工业污染形势严峻，城市空气质量总体变差的趋势尚未得到有效遏制；随着交通运输现代化的迅速发展，中国区域气态污染物的排放量较大(WU等, 2007; 柴发合等, 2013)，导致部分地区复合型污染加剧和区域性大气雾霾天气的频繁发生(LANG等, 2012)。2013年春季中国华北地区严重的雾霾天气已经引起社会高度关注。根据空气质量标准GB3095-2012的限值，中国目前有超过2/3的城市空气质量不达标(柴发合等, 2013)。受经济发展和城镇化进程的驱动，未来中国化石能源特别是煤炭消费量将持续增长(LANG等, 2012; 吕连宏和罗宏, 2012)，大气污染的巨大压力将持续较长时间。研究中国空气质量及其与相关因素的关系，可以为有效控制大气污染、改善空气质量提供必要的科学依据(李小飞等, 2012)。

目前，空气质量相关的时空特征研究主要集中在以下几个方面：基于机理模型的污染物质量浓度模拟(RAINHAM等, 2005)，基于GIS和遥感的空气质量时空特征分布研究(张宝春等, 2011; 吴兑, 2012)，污染物柱浓度研究(姚凌等, 2012; DING等, 2009)，基于地统计学的污染物质量浓度时空变异性研究(赵文慧等, 2010)，基于模糊理论的大气环境质量预测与评价(ONKAK-ENGIN等, 2004; SOWLAT等, 2011)，基于时间序列理论（如小波变换、浓度谱）的城市空气质量分析(孟晓艳等, 2012; 黄进和张金池, 2009; 王海鹏等, 2011; OSOWSKI和GARANTY, 2007)；污染物质量浓度与相关因素的统计相关性研究(朱李华等, 2010)，污染物质量浓度与气象因子的回归拟合(毛敏娟等, 2013; DAVIS和KALKSTEIN, 1990)，空气污染指数的神经网络预报(JIANG等, 2004)等。总结以上可知，应用时间与空间模型分析空气环境质量的研究越来越多。从中还可以看出，除去应用CMAQ等机理性模型模拟空气质量外，也有学者关注基于统计方法的空气质量预测与模拟，但是大多数研究对空间位置的影响考虑不足。地理加权回归模型（GWR）以空间位置为拟合参数，是一种相对简单而又有效的探测空间非平稳性的新方法，属于局域空间分析范畴(BRUNSDON等, 1996)。本文以2010年全国地级城市SO2年均质量浓度为例，研究GWR在大气污染物质量浓度模拟的可能性。

1 GWR模型概述

对于空间现象而言，传统的统计分析大多忽视了空间数据之间的相互依赖性，因而其结果说服力不够(苏方林, 2005)。某些情况下，空间上的依赖性比时间上更复杂，因此在传统的计量方法基础上引入空间因素成为空间计量方法的热点。GWR模型源于空间计量经济学，是考虑了距离因素影响的回归模型，也是研究地理空间异质性现象的方法。其特定区位的回归系数不再是利用全局信息获得，而是在考虑了临近空间要素影响的情况下利用邻近观测值的子样本信息进行局部回归得到(LESAGE, 2004)。GWR在普通线性回归模型的基础上，把位置因素作为回归参数（如果回归样本存在空间异质性）。GWR方法可以看做是普通线性回归模型的改进。

1.1 普通线性回归

设随机变量y与确定性变量x1，x2，…，xβ的普通线性回归模型为：

β0，β1，…，βp是p+1个未知参数，β0为回归常数，β1，…，βp为回归系数，y称为因变量，x1，x2，…，xp称为自变量，ε是随机误差，满足以下假定则可求解：

多元线性回归方程未知参数的估计一般采用普通最小二乘法。

1.2 地理加权回归

地理加权回归模型是对普通线性回归公式（1）的扩展，将数据的地理位置嵌入到回归参数之中(BRUNSDON等, 1998)，即：

这里(ui,vi)为第 i个采样点的坐标(如经纬度)；是第i个采样点上的第k个回归参数，是地理位置的函数；，为了表述方便，我们将上式简写为：

若β1k= β2k=…βnk，则地理加权回归模型就退变为前述的普通线性回归模型。

2 指标体系构建与数据来源

本研究的因变量为 2010年全国地级城市 SO2年均质量浓度；自变量选取对SO2质量浓度分布有影响的气象、植被、地形、人为因素等9个指标进行回归。指标体系如图1所示，气象因素包括各个城市所在点位多年平均温度、日照、降水3个指标，植被因素用NDVI表示，地形因素包括高程、坡度、起伏度，人为因素选择各个城市的 GDP和能源消费总量。

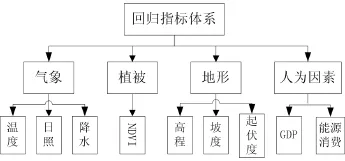
图1 回归分析指标体系Fig. 1 Index system of the regression analysis

全国地级城市 SO2年均质量浓度数据来自《2006─2010中国环境质量报告》；温度、日照、降水等气象数据来自中国气象台站，为全国700多个气象站点的数据平均并插值的结果；NDVI数据来自中科院地理所资源数据中心，通过2008年1─7月份的SPOT VGT旬数据平均得到；高程、坡度、起伏度数据通过中科院地理所资源数据中心全国1：25万DEM提取；GDP和能源消费原始数据来自2011年国家和地方统计年鉴（2010年度数据）。

由于各指标间可能存在较强的相关性，所以先进行相关分析，发现温度、日照、降水、NDVI之间的相关系数比较大，高程、坡度、起伏度之间的相关系数较大，GDP和能源消费之间的相关系数也较大。所以用主成分分析的方法对温度、日照、降水、NDVI进行计算，得到气象植被综合指数，对高程、坡度、起伏度进行主成分计算得到地形综合指数，对GDP、能源消费进行主成分计算得到人为因素综合指数。用3个综合指数进行回归模拟。

3 结果与分析

2010年，中国大多数地级以上城市SO2年均质量浓度在0.02～0.06 mg·m-3之间，属于空气质量标准GB3095—1996的二级标准（2010年全国仍实施1996年标准）；一级标准的城市数量也较多；少量城市SO2污染严重，为三级标准。如图2所示，SO2污染严重的城市主要分布在2个区域，一个区域为京津冀、山西、陕西和内蒙古一带，另一个区域为西南部的云贵、四川一带；SO2污染较轻的城市主要分布东南沿海、东北三省和西藏、新疆部分地区。

3.1 普通线性回归

通过普通线性回归拟合中国 2010年地级城市SO2年均质量浓度，拟合结果如图 3(a)所示。拟合的 SO2年均质量浓度在三级标准以上(＞=0.06 mg·m-3)和质量浓度较低(＜=0.01 mg·m-3)的城市数量较少，质量浓度为0.01～0.02 mg·m-3之间的城市数量也较少，绝大多数城市的质量浓度在0.02～0.06 mg·m-3之间，属于二级标准。与图2进行对比，发现普通线性回归拟合结果较差。

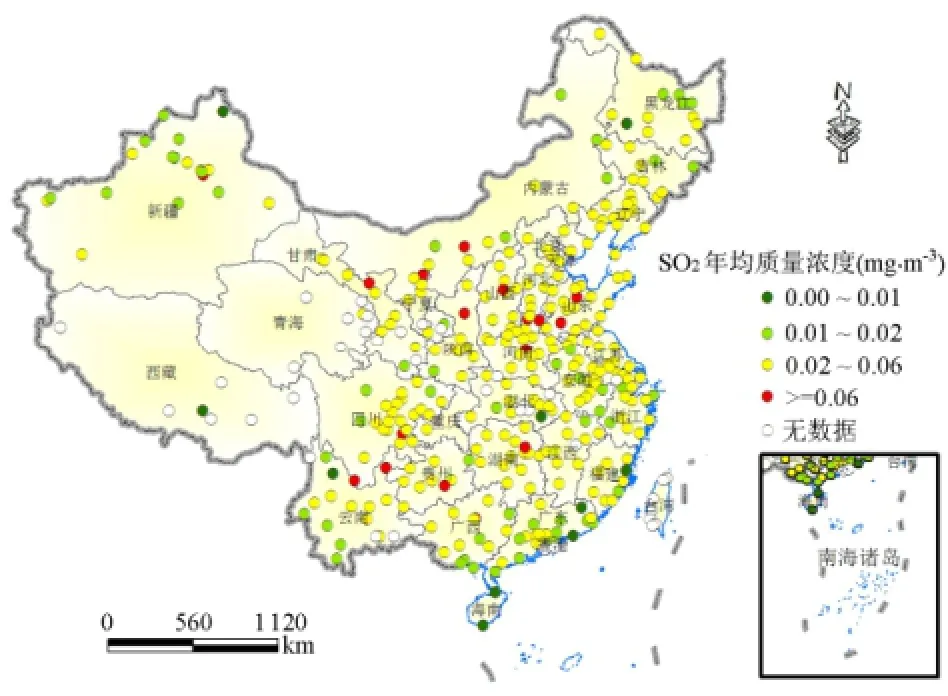
图2 2010年中国地级以上城市SO2年均质量浓度Fig. 2 Annual average concentration of SO2of prefecture-level cities in 2010

从图3(b)中可以看出，大部分城市普通线性回归结果残差较大（图中紫色和红色部分），这些城市主要在华北及其北部一带和四川盆地、云贵高原地区分布；残差较小的城市主要位于长三角和东南沿海地区（绿色部分）。通过与图 2比较发现，回归残差较大的城市与SO2年均质量浓度数值较大的城市分布有一定的重合。

3.2 GWR回归

应用ARCInfo工具的GWR拟合结果如图4所示。拟合结果中有7个城市SO2年均质量浓度超过三级标准（≥0.06 mg·m-3），用红色表示；质量浓度较低的城市有9个（＜0.01 mg·m-3），用深绿色表示；质量浓度在 0.01～0.02 mg·m-3之间的城市个数较多，用浅绿色表示；质量浓度在 0.02～0.06 mg·m-3之间的城市个数最多，用黄色表示。通过与图2对比发现，各城市的拟合结果分布规律与实测值较相似，即京津冀地区和四川盆地、云贵高原地区部分城市SO2质量浓度较高，质量浓度较低的城市多分布在东南沿海。

图3 2010年中国地级以上城市SO2年均质量浓度普通线性回归结果及其误差Fig. 3 Ordinary regression results and residuals of annual average concentration of SO2of prefecture-level cities in 2010

图4 2010年中国地级以上城市SO2年均质量浓度GWR回归结果及其拟合优度Fig. 4 GWR results and residuals of annual average concentration of SO2of prefecture-level cities in 2010

回归拟合优度用于检验模型对样本观测值的拟合程度，拟合优度越高，模型模拟效果越好；反之，模拟效果越差。当解释变量为多元时，要使用调整的拟合优度，以解决变量元素增加对拟合优度的影响。图4(b)表明长三角、湖北湖南到广东一带城市的拟合优度较高，模型拟合效果较好；京津冀及周边地区、东南和西南部分地区拟合优度较低，拟合效果较差。

3.3 普通线性回归与地理加权回归结果比较

通过图3和图4对比，发现地理加权回归拟合效果比普通线性回归要好很多。定量评估拟合模型性能的参数有r2、校正的r2等。r2是拟合度的一种度量，其值在0.0到1.0范围内变化，值越大拟合效果越好。此值可解释为回归模型所涵盖的因变量方差的比例。表1为普通线性回归和GWR的拟合优度比较，普通线性回归的r2为0.1144，校正的r2为0.1070，拟合效果很差；GWR的r2为0.6595，校正的r2为0.4742，比普通线性回归的精度有很大提高。

表1 普通线性回归与GWR拟合优度Table 1 The superiority of the ordinary regression and GWR

4 讨论与结论

4.1 讨论

通过研究发现，2010年中国地级城市的 SO2年均质量浓度存在一定程度的空间聚集特性(卢亚灵等, 2012)，这说明在用统计方法对其进行模拟时，应该考虑地理位置与区域差异的影响。通过普通线性回归与GWR拟合结果对比发现，对于中国SO2空气质量，GWR的回归结果确实要明显好于前者。但是就本研究数据来看，GWR对质量浓度数值较高城市的拟合效果较差（普通线性回归亦是）。本研究数据表明，中国SO2年均质量浓度较高的地区主要集中在华北和南部偏西地区，这也是拟合效果较差的城市所在区域；拟合效果较好的地区主要集中在长江流域和珠三角地区，这些地区SO2质量在全国相对较好。普通线性回归拟合效果很差，不适合进行此类拟合。

本研究存在一定的不足，导致GWR拟合优度下降。由于数据可得性限制，在气象要素中，缺少风速、风向等数据，虽然通过日照、温度、降水计算得出的综合指数可以在一定程度上反映不同城市的气象特征，但是与基于机理的空气质量模型有出入；在人为因素中，采用 GDP和能源消费表征经济、人口活动的影响，没有采用污染物排放量（部分城市的数据不可得），但是GDP和能源消费与污染物排放量具有很大程度的正相关，因此可以用这2个指标代替污染排放量。

本研究的结果表明，对于具有空间属性且相互之间因距离存在相互影响的空气环境质量，也可以采用GWR进行拟合。根据以往经验，相对CMAQ等基于机理的模拟模型，基于统计的GWR拟合模型与之各有优缺点。前者在对数据获取及其规范化方面要求很高，软硬件条件要求也很高，模型运行时间很长；后者对数据及其规范化及软硬件的要求较低，模拟时间也非常短。

4.2 结论

2010年，中国大多数地级以上城市SO2年均质量浓度属于GB3095—1996空气质量标准的二级。SO2污染严重的城市主要分布在华北平原及其附近和西南部的云贵、四川一带；空气质量较好的城市在南部沿海分布较为集中。中国地级以上城市空气质量分布具有空间聚集性。以地级以上城市SO2年均质量浓度为自变量，以年均温度、日照、降水、植被、地形、GDP和能源消费总量等为因变量，分别采用普通线性回归和GWR进行模拟。普通线性回归的结果很差，与现状数据对比，基本反映不出不同城市SO2年均质量浓度分布规律；GWR结果相比普通线性回归要好很多，基本能够反映不同城市SO2年均质量浓度的区域分布特征。通过对比2种模拟方法的 r2，前者为 0.1144（校正的 r2为0.1070），后者为 0.6595（校正的 r2为 0.4742），表明普通线性回归在此类模拟中不可用，GWR结果相对较好。通过分析GWR拟合优度的空间分布发现，SO2年均质量浓度数值高的地区拟合结果较差，质量浓度低的地区拟合结果相对较好。通过讨论基于GWR和基于机理的空气质量模拟模型，发现两者各有优缺点，可根据具体情况适当选择。

BRUNSDON C, FOTHERINGHAM A S, CHARLTON M E. 1996. Geographically weighted regression: a method for exploring spatial nonstationarity[J]. Geographical analysis, 28(4): 281-298.

BRUNSDON C, FOTHERINGHAM S, CHARLTON M. 1998. Geographically weighted regression[J]. Journal of the Royal Statistical Society: Series D (The Statistician), 47(3): 431-443.

DAVIS R E, KALKSTEIN L S. 1990. Using a spatial synoptic climatological classification to assess changes in atmospheric pollution concentration[J]. Physical Geography, 11(4): 320-342.

DING A, WANG T, XUE L, et al. 2009. Transport of north China air pollution by midlatitude cyclones: Case study of aircraft measurements in summer 2007[J]. Journal of Geophysical Research, 114(D8): D08304.

JEONG S L, YOUNG J K, BONGJAE K, et al. 2005. Simultaneous measurements of atmospheric pollutants and visibility with a long path DOAS system in urban areas [J]. Environmental Monitoring and Assessment, 104(1): 281-293.

JIANG D, ZHANG Y, HU X, et al. 2004. Progress in developing an ANN model for air pollution index forecast [J]. Atmospheric Environment, 38(40): 7055-7064.

KAN H D, CHEN B H. 2004. Particulate air pollution in urban areas of Shanghai China: health-based economic assessment[J]. Science of the Total Environment, 322(1): 71-79.

LANG J L, CHENG S Y, WEI W, et al. 2012. A Study on the Trends of Vehicular Emissions in the Beijing-Tianjin-Hebei (BTH) region, China [J]. Atmospheric Environment, 41(62): 605-614.

LESAGE J P. 2004. A family of geographically weighted regression models[M]//Advances in spatial econometrics. Berlin: Springer Berlin Heidelberg: 241-264.

ONKAL-ENGIN G, DEMIR I, HIZ H. 2004. Assessment of urban air quality in Istanbul using fuzzy synthetic evaluation[J]. Atmospheric Environment, 38(23): 3809-3815.

OSOWSKI S, GARANTY K. 2007. Forecasting of the daily meteorological pollution using wavelets and support vector machine[J]. Engineering Applications of Artificial Intelligence, 20(6): 745-755.

RAINHAM D G C, SMOYER-TOMIC K E, SHERIDAN S C, et al. 2005. Synoptic weather patterns and modification of the association between air pollution and human mortality[J]. International Journal of Environmental Health Research, 15(5): 347-360.

SOWLAT M H, GHARIBI H, YUNESIAN M, et al. 2011. A novel, fuzzy-based air quality index (FAQI) for air quality assessment[J]. Atmospheric Environment, 45(12): 2050-2059.

WU D, BI X Y, DENG X J, et al. 2007. Effect of atmospheric haze on the deterioration of visibility over the Pearl River Delta[J]. Acta Meteorologica Sinica, 21(2): 215-223.

ZHANG M, SONG Y, CAI X. 2007. A health based assessment of particulate air pollution in urban areas of Beijing in 2000-2004[J]. Science of the Total Environment, 376(1-3): 100-108.

ZHANG Y H, CHEN C H, CHEN G H, et al. 2006. Application of DALYs in measuring health effect of ambient air pollution: a case study in Shanghai, China[J]. Biomedical and Environmental Sciences, 19(4): 268-272.

柴发合, 李艳萍, 乔琦, 等. 2013. 我国大气污染联防联控环境监管模式的战略转型[J]. 环境保护, 5: 22-24.

黄进, 张金池. 2009. 苏州市空气质量的时间序列变化过程研究[J]. 环境科学与技术, 32(6): 49-52.

李小飞, 张明军, 王圣杰,等. 2012. 中国空气污染指数变化特征及影响因素分析[J]. 环境科学, 33(6): 1936-1943.

卢亚灵, 蒋洪强, 张静. 2012. 中国地级以上城市SO2年均质量浓度时空特征分析[J]. 生态环境学报, 21(12): 1971-1974.

吕连宏, 罗宏. 2012. 中国大气环境质量概况与污染防治新思路[J]. 中国能源, 34(1): 18-21.

毛敏娟, 刘厚通, 徐宏辉, 等. 2013. 多元观测资料融合应用的灰霾天气关键成因研究[J]. 环境科学学报, 33(3): 806-813.

孟晓艳, 王瑞斌, 张欣, 等. 2012. 2006-2010年环保重点城市主要污染物浓度变化特征[J]. 环境科学研究, 25(6): 622-627.

苏方林. 2005. 中国R&D与经济增长的空间统计分析[D]. 上海: 华东师范大学: 20-21.

王海鹏, 张斌, 刘祖涵, 等. 2011. 基于小波变换的兰州市近十年空气污染指数变化[J]. 环境科学学报, 31(5): 1070-1076.

吴兑, 廖碧婷, 吴晟, 等. 2012. 2010年广州亚运会期间灰霾天气分析[J].环境科学学报, 32(3): 521-527.

姚凌, 吕宁, 师华定. 2012. 利用SCIAMACHY遥感资料研究我国NO2柱浓度及其时空分布[J]. 环境科学研究, 25(4): 419-424.

张宝春, 陈彦军, 李伟铿, 等. 2011. 基于GIS的珠三角区域空气质量时空特征研究[J]. 生态环境学报, 20(4): 600-605.

赵文慧, 宫辉力, 赵文吉, 等. 2010. 基于地统计学的北京市可吸入颗粒物时空变异性及气象因素分析[J]. 环境科学学报, 30(11): 2154-2163.

朱李华, 陶俊, 张仁健, 等. 2010. 冬夏季广州城区碳气溶胶特征及其与O3和气象条件的关联[J]. 环境科学学报, 30(10): 1942-1949.

Simulation of Annual Average SO2Concentration of the Prefecture-level Cities in China Based on GWR Mode

LU Yaling1, JIANG Hongqiang1*, HUANG Jixia2, XU Lifen3

1. State Environmental Protection Key Laboratory of Environmental Planning and Policy Simulation, Chinese Academy for Environmental Planning, Beijing 100012, China;
2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Beijing 100101, China;
3. Key Laboratory of Analysis and Simulation of Earth Surface Processes, Ministry of Education, College of Urban and Environmental Sciences, Peking University, Beijing 100871, China

The problems of city air pollution have attracted worldwide attention. There’re various kinds of researches on air pollution, while very few of them are on the air quality regression considering the space location as the fitting parameter. This research respectively applies ordinary linear regression and geographically weighted regression model (GWR) to simulate the annual average SO2concentration of the prefecture-level cities in 2010 in China, with annual average SO2concentration as the dependent variable. The effect of spatial location is considered and taken as a regression parameter in the GWR. The indicator system of independent variables in the research includes meteorological factors (annual average temperature, sunlight, rainfall), vegetation cover (NDVI), topography (slope, slope aspect e, relief) and human factors (GDP, energy consumption). As there is a strong correlation among the indicators, the principal component analysis method is adopted to calculate these comprehensive indexes: the meteorological & vegetation index represented by temperature, sunlight, precipitation and NDVI; the topographic index represented by the elevation, slope and relief; and the human factors index represented by GDP and energy consumption. The regression simulation is conducted with these three comprehensive indexes as independent variables. Compared with the ordinary regression model, whose r2is 0.11 and corrected r2is 0.10, the simulation result of GWR model is better with much improved fitting. Its r2is 0.66, and corrected r2is 0.47. Therefore, geographically weighted regression is suitable for this kind of fitting, while the ordinary linear regression is not. By comparing the fitting in each city, we found the cities with higher annual average SO2concentration had poor fitting effects, which were mainly concentrated in North China and South China. Compared with the models based on the mechanism, the GWR model has its own advantages, such as lower requirements of data and formatting, low requirements of computer software and hardware conditions, and faster speed of operation, and so on.

prefecture-level city; geographically weighted regression (GWR); SO2; annual average concentration

X51

：A

：1674-5906（2014）08-1305-06

卢亚灵，蒋洪强，黄季夏，徐丽芬. 基于GWR的中国地级城市SO2年均质量浓度模拟[J]. 生态环境学报, 2014, 23(8): 1305-1310.

LU Yaling, JIANG Hongqiang, HUANG Jixia, XU Lifen. Simulation of Annual Average SO2Concentration of the Prefecture-level Cities in China Based on GWR Mode [J]. Ecology and Environmental Sciences, 2014, 23(8): 1305-1310.

环保公益性行业科研专项经费(201209037)；环境规划院青年科技创新基金项目“环境规划时空数据挖掘技术及其应用研究”

卢亚灵(1984年生)，女，助理研究员，硕士，主要从事大气环境相关研究。E-mail: luyl@caep.org.cn

*通讯作者：jianghq@caep.org.cn

2013-12-01